Was sind rekurrente neuronale Netze (RNN)?
Ein rekurrentes neuronales Netzwerk (RNN) ist die Art von künstlichem neuronalem Netzwerk (ANN), die in Apples Siri und Googles Sprachsuche verwendet wird. RNN erinnern sich dank eines internen Speichers an vergangene Eingaben, was für die Vorhersage von Aktienkursen, die Generierung von Texten, Transkriptionen und maschinelle Übersetzungen nützlich ist.
Im traditionellen neuronalen Netz sind die Eingänge und die Ausgänge unabhängig voneinander, während der Ausgang im RNN von früheren Elementen innerhalb der Sequenz abhängig ist. Rekurrente Netze teilen sich auch Parameter in jeder Schicht des Netzes. In Feedforward-Netzen gibt es unterschiedliche Gewichte für jeden Knoten. Während RNN in jeder Schicht des Netzes die gleichen Gewichte verwendet, werden die Gewichte und die Basis während des Gradientenabstiegs individuell angepasst, um den Verlust zu reduzieren.
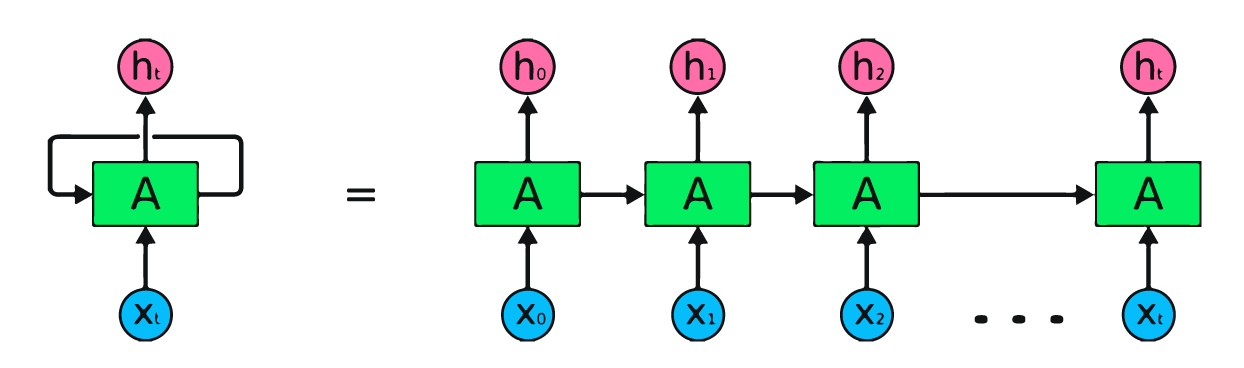
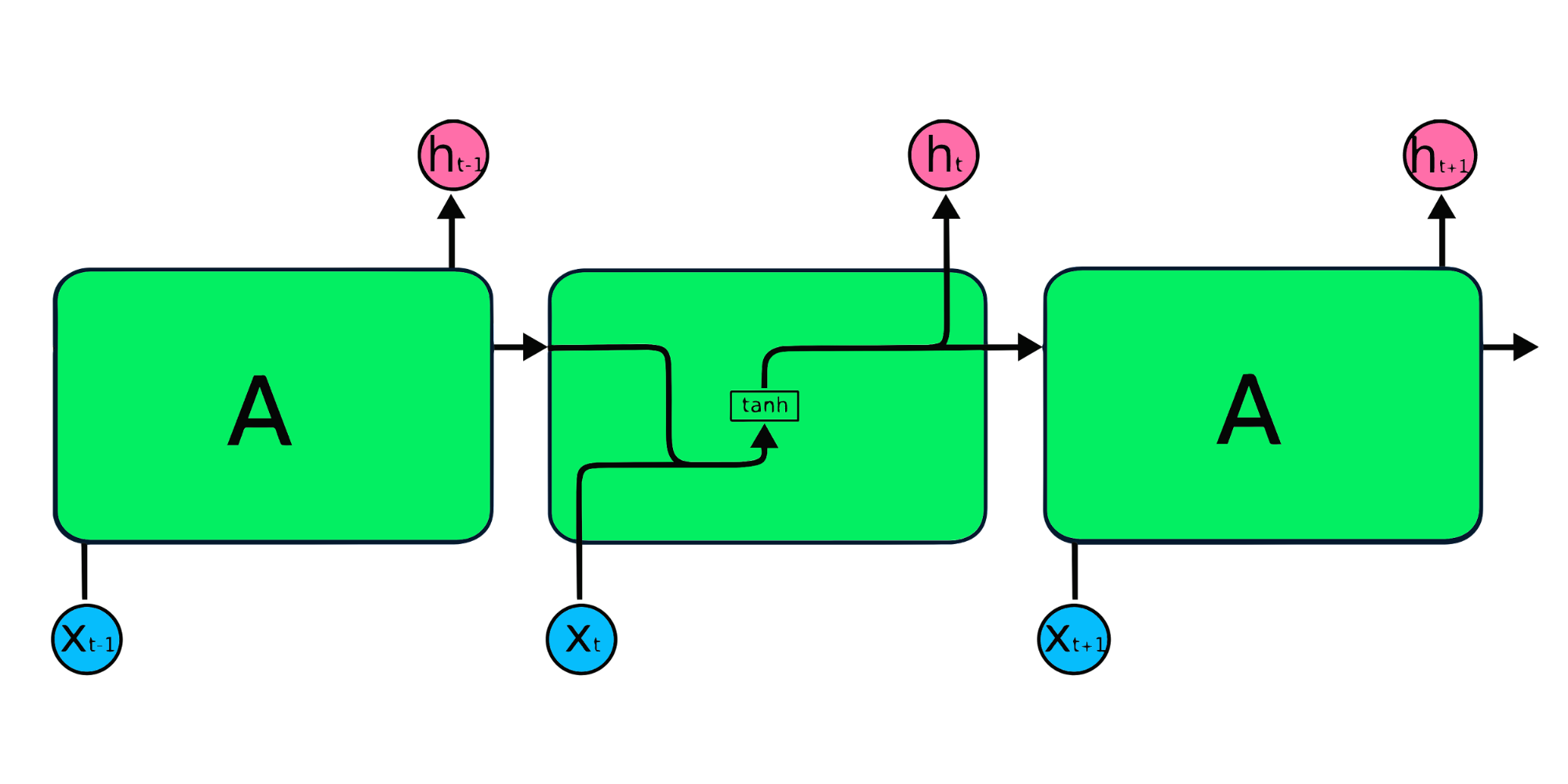
Das Bild oben ist eine einfache Darstellung von rekurrenten neuronalen Netzen. Wenn wir Aktienkurse anhand einfacher Daten [45,56,45,49,50,...] prognostizieren, enthält jede Eingabe von X0 bis Xt einen Wert aus der Vergangenheit. X0 hat zum Beispiel die Zahl 45, X1 die Zahl 56, und diese Werte werden verwendet, um die nächste Zahl in einer Folge vorherzusagen.
Wie rekurrente neuronale Netze funktionieren
In RNN durchlaufen die Informationen die Schleife, sodass die Ausgabe durch die aktuelle Eingabe und die zuvor erhaltenen Eingaben bestimmt wird.
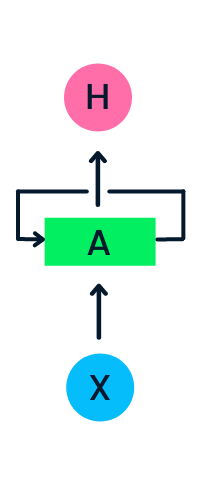
Die Eingabeschicht X verarbeitet die anfängliche Eingabe und leitet sie an die mittlere Schicht A weiter. Die mittlere Schicht besteht aus mehreren versteckten Schichten, jede mit eigenen Aktivierungsfunktionen, Gewichten und Vorspannungen. Diese Parameter werden für die versteckte Schicht vereinheitlicht, so dass statt mehrerer versteckter Schichten nur eine erstellt wird und diese in einer Schleife durchlaufen wird.
Anstelle der traditionellen Backpropagation verwenden rekurrente neuronale Netze Backpropagation through Time (BPTT) Algorithmen, um den Gradienten zu bestimmen. Bei der Backpropagation passt das Modell die Parameter an, indem es Fehler von der Ausgangs- zur Eingangsschicht berechnet. BPTT summiert den Fehler bei jedem Zeitschritt, da RNN die Parameter in jeder Schicht teilt. Erfahre mehr über RNNs und wie sie funktionieren unter Was sind rekurrente neuronale Netze?
Arten von rekurrenten neuronalen Netzen
Feedforward-Netze haben nur einen Eingang und einen Ausgang, während rekurrente neuronale Netze flexibel sind, da die Länge der Ein- und Ausgänge verändert werden kann. Diese Flexibilität ermöglicht es RNNs, Musik zu erzeugen, Gefühle zu klassifizieren und maschinell zu übersetzen.
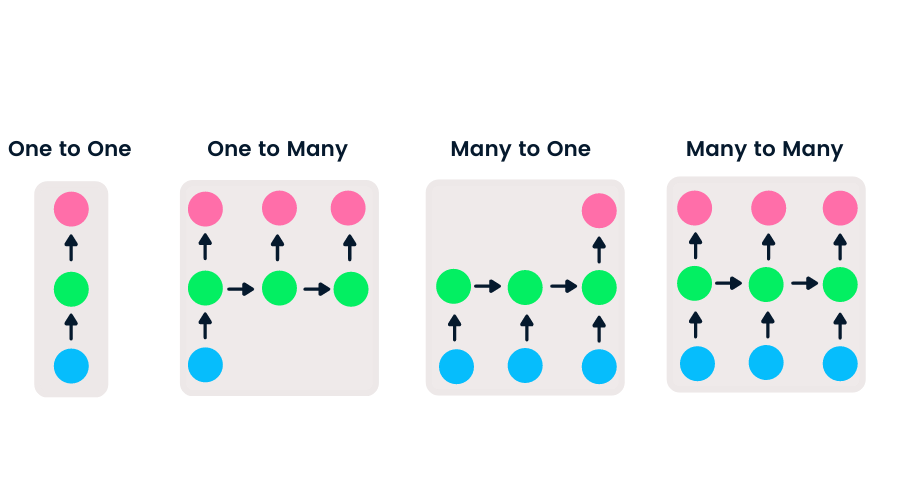
Es gibt vier Arten von RNN, die auf der unterschiedlichen Länge der Eingänge und Ausgänge basieren.
- One-to-One ist ein einfaches neuronales Netz. Sie wird häufig für maschinelle Lernprobleme verwendet, die eine einzige Eingabe und Ausgabe haben.
- One-to-many hat einen einzigen Eingang und mehrere Ausgänge. Dies wird für die Erstellung von Bildunterschriften verwendet.
- Many-to-One nimmt eine Folge von mehreren Eingaben und sagt eine einzige Ausgabe voraus. Sie wird häufig bei der Sentiment-Klassifizierung eingesetzt, bei der die Eingabe ein Text und die Ausgabe eine Kategorie ist.
- Many-to-many benötigt mehrere Eingänge und Ausgänge. Die häufigste Anwendung ist die maschinelle Übersetzung.
Beliebte Kurse zum Maschinellen Lernen
Einführung in Deep Learning in Python
CNN vs. RNN
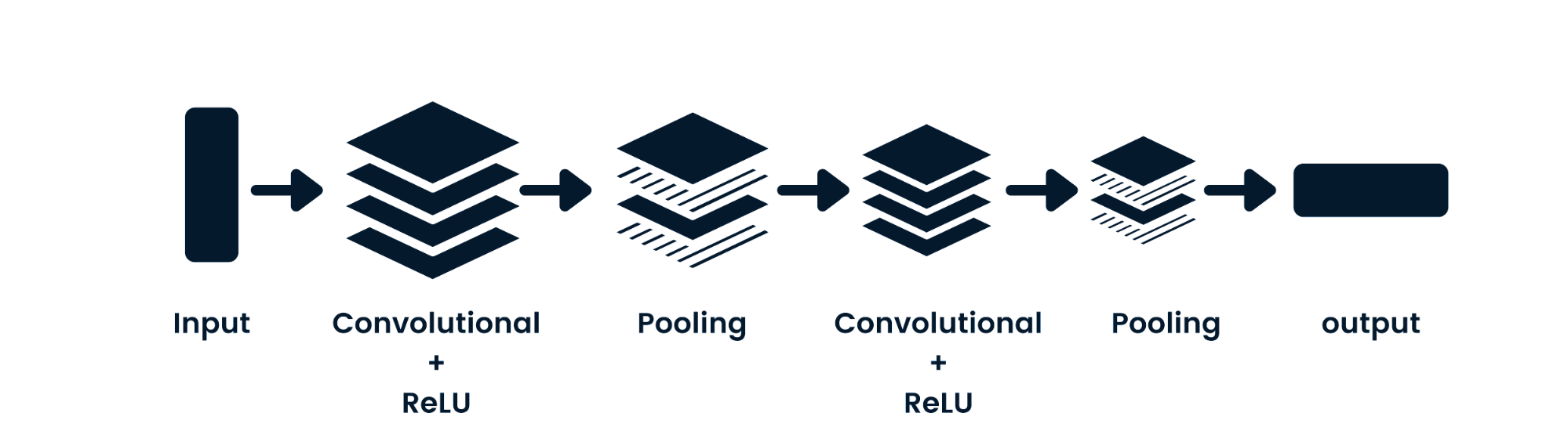
Das Convolutional Neural Network (CNN) ist ein neuronales Netzwerk mit Vorwärtskopplung, das räumliche Daten verarbeiten kann. Sie wird häufig für Computer-Vision-Anwendungen wie die Bildklassifizierung verwendet. Die einfachen neuronalen Netze sind gut bei einfachen binären Klassifizierungen, aber sie können keine Bilder mit Pixelabhängigkeiten verarbeiten. Die Architektur des CNN-Modells besteht aus Faltungsschichten, ReLU-Schichten, Pooling-Schichten und vollständig verbundenen Ausgabeschichten. Du kannst CNN lernen, indem du an einem Projekt wie " Convolutional Neural Networks in Python" arbeitest.
Hauptunterschiede zwischen CNN und RNN
- CNN ist für spärliche Daten wie Bilder geeignet. RNN ist für Zeitreihen und sequentielle Daten geeignet.
- Beim Trainieren des Modells verwendet CNN eine einfache Backpropagation und RNN verwendet Backpropagation über die Zeit, um den Verlust zu berechnen.
- Bei RNN gibt es keine Längenbeschränkung für Eingänge und Ausgänge, aber bei CNN sind die Eingänge und Ausgänge endlich.
- CNN hat ein Feedforward-Netzwerk und RNN arbeitet mit Schleifen, um sequentielle Daten zu verarbeiten.
- CNN kann auch für die Video- und Bildverarbeitung eingesetzt werden. RNN wird hauptsächlich für die Sprach- und Textanalyse verwendet.
Einschränkungen von RNN
Bei einfachen RNN-Modellen gibt es in der Regel zwei große Probleme. Diese Probleme hängen mit dem Gradienten zusammen, der die Steigung der Verlustfunktion zusammen mit der Fehlerfunktion darstellt.
- Das Problem des verschwindenden Gradienten tritt auf, wenn der Gradient so klein wird, dass die Aktualisierung der Parameter unbedeutend wird; schließlich hört der Algorithmus auf zu lernen.
- Das Problem des explodierenden Gradienten tritt auf, wenn der Gradient zu groß wird, wodurch das Modell instabil wird. In diesem Fall häufen sich größere Fehlergradienten an, und die Modellgewichte werden zu groß. Dieses Problem kann zu längeren Trainingszeiten und schlechter Modellleistung führen.
Die einfache Lösung für diese Probleme besteht darin, die Anzahl der versteckten Schichten innerhalb des neuronalen Netzes zu reduzieren, was die Komplexität der RNNs verringert. Diese Probleme können auch durch den Einsatz fortschrittlicher RNN-Architekturen wie LSTM und GRU gelöst werden.
Erweiterte RNN-Architekturen
Die einfachen RNN-Wiederholungsmodule haben eine Grundstruktur mit einer einzigen tanh-Schicht. Die einfache RNN-Struktur leidet unter einem kurzen Gedächtnis, da sie Schwierigkeiten hat, die Informationen des vorherigen Zeitschritts in größeren sequenziellen Daten zu behalten. Diese Probleme können durch das Langzeitgedächtnis (Long Short Term Memory, LSTM) und die Gated Recurrent Unit (GRU) leicht gelöst werden, da sie in der Lage sind, sich lange Zeiträume von Informationen zu merken.
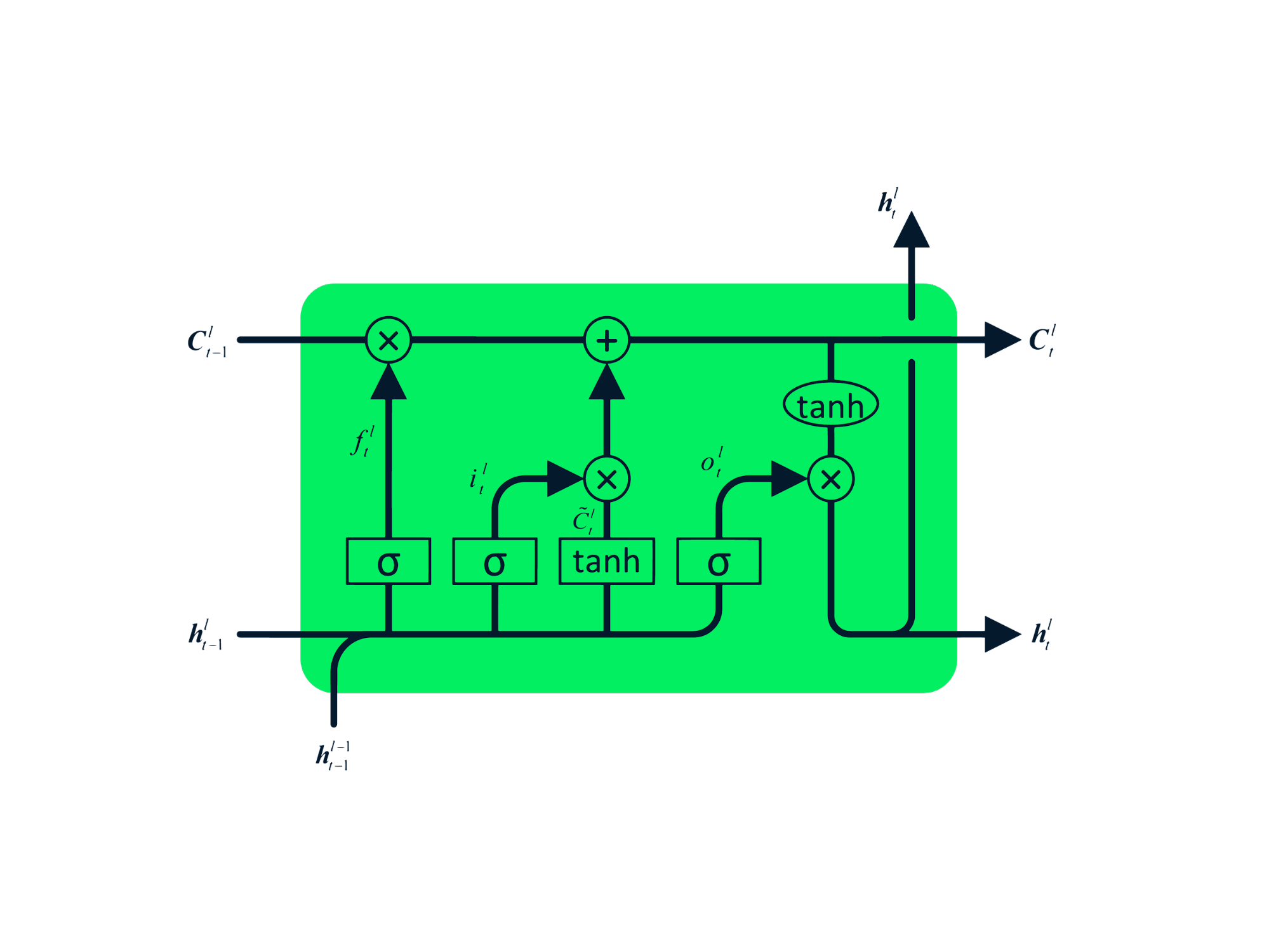
Langes Kurzzeitgedächtnis (LSTM)
Das Long Short Term Memory (LSTM) ist ein fortschrittlicher Typ von RNN, der entwickelt wurde, um sowohl das Problem des zerfallenden als auch des explodierenden Gradienten zu vermeiden. Genau wie RNN hat LSTM sich wiederholende Module, aber die Struktur ist anders. Anstelle einer einzigen Tanh-Schicht hat die LSTM vier interagierende Schichten, die miteinander kommunizieren. Diese vierschichtige Struktur hilft dem LSTM, das Langzeitgedächtnis zu bewahren, und kann bei verschiedenen sequentiellen Problemen wie maschineller Übersetzung, Sprachsynthese, Spracherkennung und Handschrifterkennung eingesetzt werden. Du kannst praktische Erfahrungen mit LSTM sammeln, indem du die Anleitung befolgst: Python LSTM für Aktienvorhersagen.
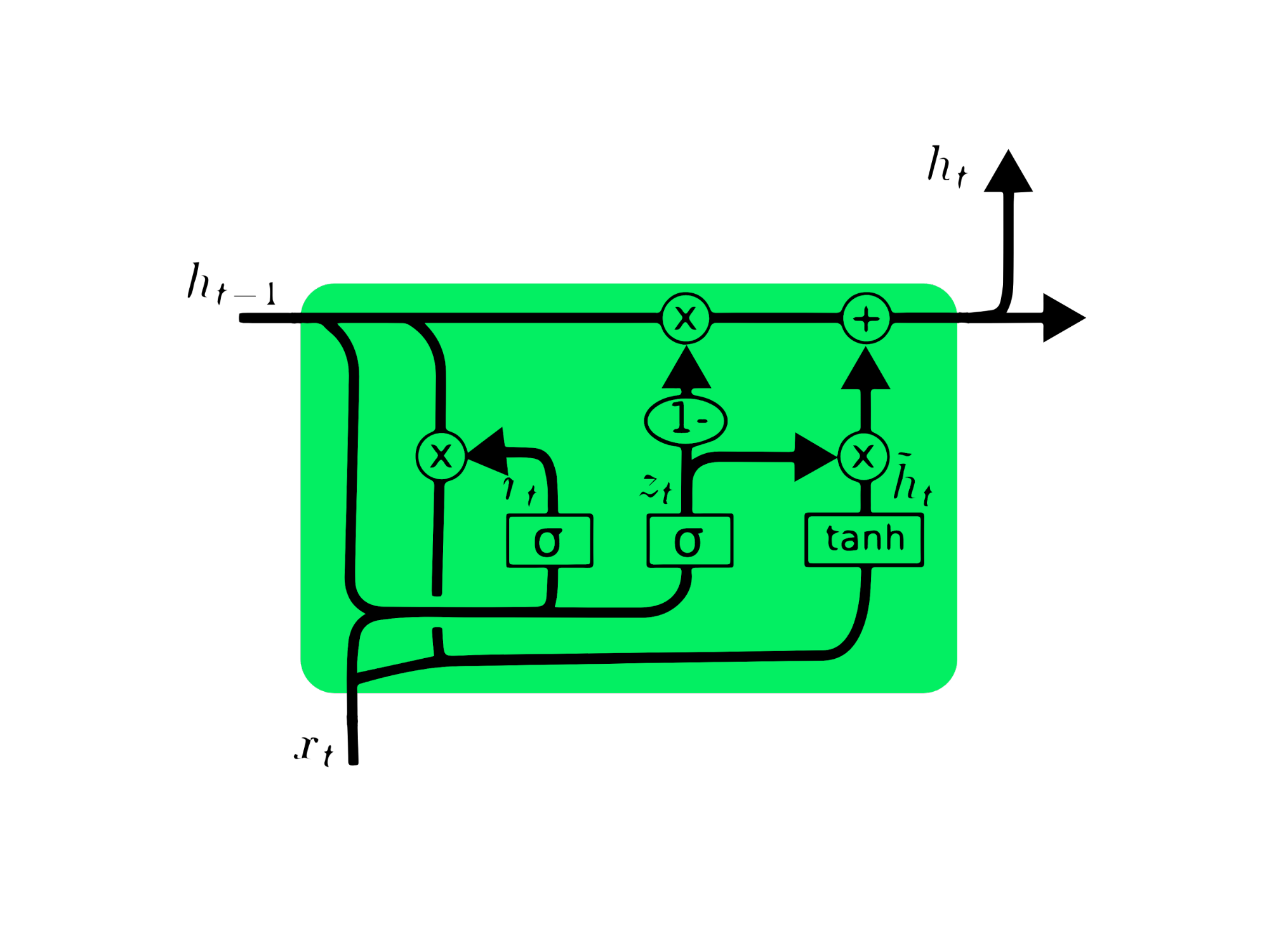
Gated Recurrent Unit (GRU)
Die Gated Recurrent Unit (GRU) ist eine Abwandlung der LSTM, da beide Ähnlichkeiten im Design aufweisen und in einigen Fällen ähnliche Ergebnisse liefern. GRU verwendet ein Update-Gate und ein Reset-Gate, um das Problem des verschwindenden Gradienten zu lösen. Diese Gates entscheiden, welche Informationen wichtig sind und geben sie an den Ausgang weiter. Die Gates können darauf trainiert werden, Informationen zu speichern, die lange zurückliegen, ohne dass sie mit der Zeit verschwinden oder irrelevante Informationen entfernt werden.
Im Gegensatz zum LSTM hat die GRU keinen Zellzustand Ct. Es hat nur einen versteckten Zustand ht, und aufgrund der einfachen Architektur hat GRU im Vergleich zu LSTM-Modellen eine geringere Trainingszeit. Die GRU-Architektur ist einfach zu verstehen, denn sie nimmt die Eingabe xt und den versteckten Zustand vom vorherigen Zeitstempel ht-1 und gibt den neuen versteckten Zustand ht aus. Ausführliche Informationen über GRU findest du unter GRU-Netzwerke verstehen.
MasterCard Stock Price Prediction Using LSTM & GRU
In diesem Projekt werden wir den MasterCard-Aktiendatensatz von Kaggle vom 25. Mai 2006 bis zum 11. Oktober 2021 verwenden und die LSTM- und GRU-Modelle zur Vorhersage des Aktienkurses trainieren. Dies ist ein einfaches, projektbasiertes Tutorial, in dem wir Daten analysieren, vorverarbeiten, um sie auf fortgeschrittene RNN-Modelle zu trainieren, und schließlich die Ergebnisse auswerten werden.
Das Projekt benötigt Pandas und Numpy für die Datenbearbeitung, Matplotlib.pyplot für die Datenvisualisierung, scikit-learn für die Skalierung und Auswertung und TensorFlow für die Modellierung. Wir werden auch den Grundstein für die Reproduzierbarkeit legen.
# Importing the libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM, Dropout, GRU, Bidirectional
from tensorflow.keras.optimizers import SGD
from tensorflow.random import set_seed
set_seed(455)
np.random.seed(455)
Datenanalyse
In diesem Teil werden wir den MasterCard-Datensatz importieren, indem wir die Datumsspalte zum Index hinzufügen und in das DateTime-Format konvertieren. Wir werden auch irrelevante Spalten aus dem Datensatz streichen, da wir nur an den Aktienkursen, dem Volumen und dem Datum interessiert sind.
Der Datensatz hat das Datum als Index und Open, High, Low, Close und Volume als Spalten. Es sieht so aus, als hätten wir erfolgreich einen bereinigten Datensatz importiert.
dataset = pd.read_csv(
"data/Mastercard_stock_history.csv", index_col="Date", parse_dates=["Date"]
).drop(["Dividends", "Stock Splits"], axis=1)
print(dataset.head())
Open High Low Close Volume
Date
2006-05-25 3.748967 4.283869 3.739664 4.279217 395343000
2006-05-26 4.307126 4.348058 4.103398 4.179680 103044000
2006-05-30 4.183400 4.184330 3.986184 4.093164 49898000
2006-05-31 4.125723 4.219679 4.125723 4.180608 30002000
2006-06-01 4.179678 4.474572 4.176887 4.419686 62344000
Die Funktion .describe() hilft uns, die Daten eingehend zu analysieren. Konzentrieren wir uns auf die Spalte Hoch, da wir sie zum Trainieren des Modells verwenden werden. Wir können auch die Spalten "Close" oder " Open" für ein Modellmerkmal wählen, aber "High" macht mehr Sinn, da es uns Informationen darüber liefert, wie hoch die Werte der Aktie an dem jeweiligen Tag gestiegen sind.
Der niedrigste Aktienkurs liegt bei 4,10 $ und der höchste bei 400,5 $. Der Mittelwert liegt bei $105,9 und die Standardabweichung bei $107,3, was bedeutet, dass die Aktien eine hohe Varianz haben.
print(dataset.describe())
Open High Low Close Volume
count 3872.000000 3872.000000 3872.000000 3872.000000 3.872000e+03
mean 104.896814 105.956054 103.769349 104.882714 1.232250e+07
std 106.245511 107.303589 105.050064 106.168693 1.759665e+07
min 3.748967 4.102467 3.739664 4.083861 6.411000e+05
25% 22.347203 22.637997 22.034458 22.300391 3.529475e+06
50% 70.810079 71.375896 70.224002 70.856083 5.891750e+06
75% 147.688448 148.645373 146.822013 147.688438 1.319775e+07
max 392.653890 400.521479 389.747812 394.685730 3.953430e+08
Mit .isna().sum() können wir die fehlenden Werte im Datensatz ermitteln. Es scheint, dass der Datensatz keine fehlenden Werte enthält.
dataset.isna().sum()
Open 0
High 0
Low 0
Close 0
Volume 0
dtype: int64
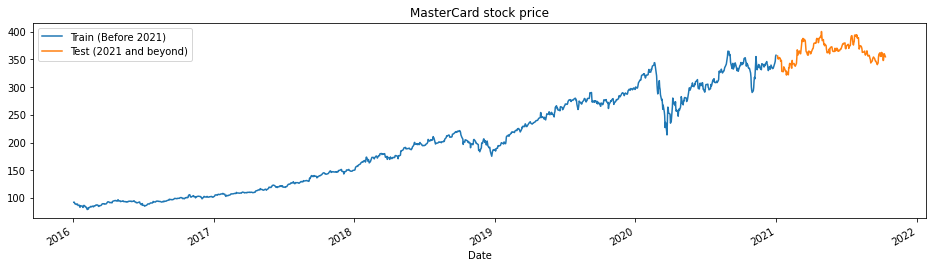
Die Funktion train_test_plot benötigt drei Argumente: dataset, tstart und tend und zeichnet ein einfaches Liniendiagramm. Die Angaben tstart und tend sind Zeitgrenzen in Jahren. Wir können diese Argumente ändern, um bestimmte Zeiträume zu analysieren. Das Liniendiagramm ist in zwei Teile unterteilt: Training und Test. So können wir die Verteilung des Testdatensatzes bestimmen.
Die Aktienkurse von MasterCard sind seit 2016 gestiegen. Im ersten Quartal 2020 gab es einen Einbruch, aber in der zweiten Jahreshälfte hat er sich stabilisiert. Unser Testdatensatz besteht aus einem Jahr, von 2021 bis 2022, und der Rest des Datensatzes wird zum Training verwendet.
tstart = 2016
tend = 2020
def train_test_plot(dataset, tstart, tend):
dataset.loc[f"{tstart}":f"{tend}", "High"].plot(figsize=(16, 4), legend=True)
dataset.loc[f"{tend+1}":, "High"].plot(figsize=(16, 4), legend=True)
plt.legend([f"Train (Before {tend+1})", f"Test ({tend+1} and beyond)"])
plt.title("MasterCard stock price")
plt.show()
train_test_plot(dataset,tstart,tend)
Datenvorverarbeitung
Die Funktion train_test_split teilt den Datensatz in zwei Teilmengen: training_set und test_set.
def train_test_split(dataset, tstart, tend):
train = dataset.loc[f"{tstart}":f"{tend}", "High"].values
test = dataset.loc[f"{tend+1}":, "High"].values
return train, test
training_set, test_set = train_test_split(dataset, tstart, tend)
Wir werden die Funktion MinMaxScaler verwenden, um unser Trainingsset zu standardisieren, was uns hilft, Ausreißer oder Anomalien zu vermeiden. Du kannst auch StandardScaler oder eine andere skalare Funktion verwenden, um deine Daten zu normalisieren und die Modellleistung zu verbessern.
sc = MinMaxScaler(feature_range=(0, 1))
training_set = training_set.reshape(-1, 1)
training_set_scaled = sc.fit_transform(training_set)
Die Funktion split_sequence verwendet einen Trainingsdatensatz und wandelt ihn in Eingaben (X_train) und Ausgaben (y_train) um.
Wenn die Sequenz beispielsweise [1,2,3,4,5,6,7,8,9,10,11,12] lautet und n_step drei ist, wird die Sequenz in drei Eingangszeitstempel und einen Ausgang umgewandelt, wie unten gezeigt:
| X | y |
|---|---|
| 1,2,3 | 4 |
| 2,3,4 | 5 |
| 3,4,5 | 6 |
| 4,5,6 | 7 |
| … | … |
In diesem Projekt verwenden wir 60 n_steps. Wir können auch die Anzahl der Schritte reduzieren oder erhöhen, um die Modellleistung zu optimieren.
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
end_ix = i + n_steps
if end_ix > len(sequence) - 1:
break
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
n_steps = 60
features = 1
# split into samples
X_train, y_train = split_sequence(training_set_scaled, n_steps)
Wir arbeiten mit univariaten Reihen, also ist die Anzahl der Merkmale eins, und wir müssen den X_train so umformen, dass er auf das LSTM-Modell passt. Der X_train hat [Samples, Timesteps], und wir werden ihn in [Samples, Timesteps, Features] umwandeln.
# Reshaping X_train for model
X_train = X_train.reshape(X_train.shape[0],X_train.shape[1],features)
LSTM-Modell
Das Modell besteht aus einer einzelnen versteckten Schicht des LSTM und einer Ausgabeschicht. Du kannst mit der Anzahl der Einheiten experimentieren, da du mit mehr Einheiten bessere Ergebnisse erzielst. Für dieses Experiment stellen wir die LSTM-Einheiten auf 125, tanh als Aktivierung und die Eingabegröße ein.
Anmerkung des Autors: Die Tensorflow-Bibliothek ist benutzerfreundlich, so dass wir keine LSTM- oder GRU-Modelle von Grund auf erstellen müssen. Wir werden einfach die LSTM- oder GRU-Module verwenden, um das Modell zu erstellen.
Schließlich werden wir das Modell mit einem RMSprop-Optimierer und dem mittleren quadratischen Fehler als Verlustfunktion zusammenstellen.
# The LSTM architecture
model_lstm = Sequential()
model_lstm.add(LSTM(units=125, activation="tanh", input_shape=(n_steps, features)))
model_lstm.add(Dense(units=1))
# Compiling the model
model_lstm.compile(optimizer="RMSprop", loss="mse")
model_lstm.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 125) 63500
_________________________________________________________________
dense (Dense) (None, 1) 126
=================================================================
Total params: 63,626
Trainable params: 63,626
Non-trainable params: 0
_________________________________________________________________
Das Modell wird mit 50 Epochen und 32 Stapelgrößen trainiert. Du kannst die Hyperparameter ändern, um die Trainingszeit zu verkürzen oder die Ergebnisse zu verbessern. Das Modelltraining wurde erfolgreich mit dem bestmöglichen Verlust abgeschlossen.
model_lstm.fit(X_train, y_train, epochs=50, batch_size=32)
Epoch 50/50
38/38 [==============================] - 1s 30ms/step - loss: 3.1642e-04
Ergebnisse
Wir werden die Vorverarbeitung wiederholen und die Testmenge normalisieren. Zunächst werden wir den Datensatz transformieren, dann in Stichproben aufteilen, umformen, vorhersagen und die Vorhersagen in die Standardform umkehren.
dataset_total = dataset.loc[:,"High"]
inputs = dataset_total[len(dataset_total) - len(test_set) - n_steps :].values
inputs = inputs.reshape(-1, 1)
#scaling
inputs = sc.transform(inputs)
# Split into samples
X_test, y_test = split_sequence(inputs, n_steps)
# reshape
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], features)
#prediction
predicted_stock_price = model_lstm.predict(X_test)
#inverse transform the values
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
Mit der Funktion plot_predictions kannst du ein Liniendiagramm erstellen, in dem der tatsächliche Wert dem vorhergesagten Wert gegenübergestellt wird. So können wir den Unterschied zwischen den tatsächlichen und den vorhergesagten Werten sichtbar machen.
Die Funktion return_rmse nimmt Test- und Vorhersageargumente entgegen und gibt den mittleren quadratischen Fehler (root mean square error, rmse) aus.
def plot_predictions(test, predicted):
plt.plot(test, color="gray", label="Real")
plt.plot(predicted, color="red", label="Predicted")
plt.title("MasterCard Stock Price Prediction")
plt.xlabel("Time")
plt.ylabel("MasterCard Stock Price")
plt.legend()
plt.show()
def return_rmse(test, predicted):
rmse = np.sqrt(mean_squared_error(test, predicted))
print("The root mean squared error is {:.2f}.".format(rmse))
Wie die folgende Grafik zeigt, hat das einschichtige LSTM-Modell gut abgeschnitten.
plot_predictions(test_set,predicted_stock_price)
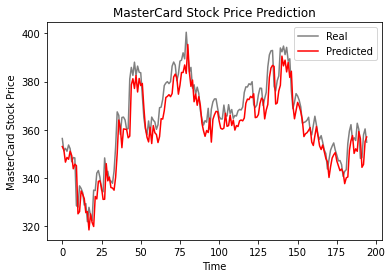
Die Ergebnisse sehen vielversprechend aus, da das Modell im Testdatensatz 6,70 rmse erreichte.
return_rmse(test_set,predicted_stock_price)
>>> The root mean squared error is 6.70.
GRU Modell
Wir lassen alles beim Alten und ersetzen nur die LSTM-Schicht durch die GRU-Schicht, um die Ergebnisse richtig vergleichen zu können. Die Modellstruktur enthält eine einzelne GRU-Schicht mit 125 Einheiten und eine Ausgabeschicht.
model_gru = Sequential()
model_gru.add(GRU(units=125, activation="tanh", input_shape=(n_steps, features)))
model_gru.add(Dense(units=1))
# Compiling the RNN
model_gru.compile(optimizer="RMSprop", loss="mse")
model_gru.summary()
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru_4 (GRU) (None, 125) 48000
_________________________________________________________________
dense_5 (Dense) (None, 1) 126
=================================================================
Total params: 48,126
Trainable params: 48,126
Non-trainable params: 0
_________________________________________________________________
Das Modell wurde erfolgreich mit 50 Epochen und einer Stapelgröße von 32 trainiert.
model_gru.fit(X_train, y_train, epochs=50, batch_size=32)
Epoch 50/50
38/38 [==============================] - 1s 29ms/step - loss: 2.6691e-04
Ergebnisse
Wie wir sehen können, liegen die realen und die vorhergesagten Werte relativ nah beieinander. Das vorhergesagte Liniendiagramm stimmt fast mit den tatsächlichen Werten überein.
GRU_predicted_stock_price = model_gru.predict(X_test)
GRU_predicted_stock_price = sc.inverse_transform(GRU_predicted_stock_price)
plot_predictions(test_set, GRU_predicted_stock_price)
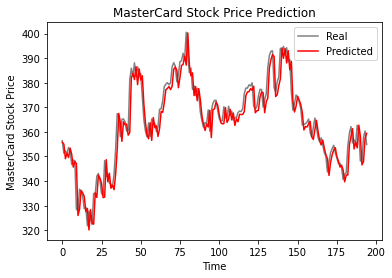
Das GRU-Modell erreichte im Testdatensatz 5,50 rmse, was eine Verbesserung gegenüber dem LSTM-Modell darstellt.
return_rmse(test_set,GRU_predicted_stock_price)
>>> The root mean squared error is 5.50.
Fazit
Die Welt bewegt sich auf hybride Lösungen zu, bei denen Datenwissenschaftler hybride CNN-RNN-Netzwerke im Bereich der Bilduntertitelung, der Emotionserkennung, der Videountertitelung und der DNA-Sequenzierung einsetzen. Hybride Netzwerke liefern sowohl visuelle als auch zeitliche Merkmale für das Modell. Erfahre mehr über RNN, indem du den Kurs besuchst: Rekurrente neuronale Netze für die Sprachmodellierung in Python.
In der ersten Hälfte des Tutoriums werden die Grundlagen rekurrenter neuronaler Netze, ihre Grenzen und Lösungen in Form fortschrittlicherer Architekturen behandelt. In der zweiten Hälfte des Tutorials geht es um die Entwicklung von MasterCard-Aktienkursvorhersagen mithilfe von LSTM- und GRU-Modellen. Die Ergebnisse zeigen deutlich, dass das GRU-Modell bei ähnlicher Struktur und ähnlichen Hyperparametern besser abschneidet als das LSTM.
Dieses Projekt ist auf dem DataCamp-Arbeitsbereich verfügbar.