Klassifizierungsverfahren sind ein wesentlicher Bestandteil von maschinellem Lernen und Data-Mining-Anwendungen. Etwa 70 % der Data-Science-Probleme sind Klassifizierungsprobleme. Es gibt viele Klassifizierungsprobleme, aber die logistische Regression ist weit verbreitet und ist eine nützliche Regressionsmethode zur Lösung des binären Klassifizierungsproblems. Eine weitere Kategorie der Klassifizierung ist die Multinomialklassifizierung, die sich mit Problemen befasst, bei denen mehrere Klassen in der Zielvariable vorhanden sind. Der IRIS-Datensatz ist ein sehr bekanntes Beispiel für eine Mehrklassen-Klassifizierung. Andere Beispiele sind die Einteilung von Artikeln/Blogs/Dokumenten in Kategorien.
Die logistische Regression kann für verschiedene Klassifizierungsprobleme verwendet werden, z. B. für die Spam-Erkennung. Einige andere Beispiele sind: Diabetesvorhersage, ob ein bestimmter Kunde ein bestimmtes Produkt kaufen wird; ob ein Kunde abwandern wird oder nicht, ob der Nutzer auf einen bestimmten Werbelink klicken wird oder nicht, und viele weitere Beispiele.
Die logistische Regression ist einer der einfachsten und am häufigsten verwendeten Algorithmen des maschinellen Lernens für die Klassifizierung in zwei Klassen. Sie ist einfach zu implementieren und kann als Grundlage für jedes binäre Klassifikationsproblem verwendet werden. Seine grundlegenden Konzepte sind auch beim Deep Learning konstruktiv. Die logistische Regression beschreibt und schätzt die Beziehung zwischen einer abhängigen binären Variable und unabhängigen Variablen.
Um den Beispielcode in diesem Lernprogramm ganz einfach selbst auszuführen, kannst du eine kostenlose DataLab-Arbeitsmappe erstellen, auf der Python vorinstalliert ist und die alle Codebeispiele enthält. Wenn du die logistische Regression weiter üben möchtest, schau dir die Übungen in unserem Kurs Kreditrisikomodellierung in R an, der viele praktische Beispiele enthält.
Was ist logistische Regression?
Die logistische Regression ist eine statistische Methode zur Vorhersage binärer Klassen. Die Ergebnis- oder Zielvariable ist dichotom. Dichotomisch bedeutet, dass es nur zwei mögliche Klassen gibt. Sie kann zum Beispiel bei Problemen mit der Krebserkennung eingesetzt werden. Sie berechnet die Wahrscheinlichkeit des Eintretens eines Ereignisses.
Sie ist ein Spezialfall der linearen Regression, bei der die Zielvariable kategorial ist. Sie verwendet den Logarithmus der Quoten als abhängige Variable. Die logistische Regression sagt die Wahrscheinlichkeit des Auftretens eines binären Ereignisses mit Hilfe einer Logit-Funktion voraus.
Lineare Regressionsgleichung:
![]()
Dabei ist y eine abhängige Variable und x1, x2 ... und Xn sind erklärende Variablen.
Sigmoid Funktion:
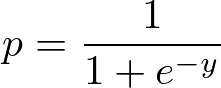
Wende die Sigmoid-Funktion auf die lineare Regression an:
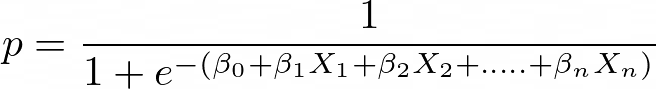
Eigenschaften der logistischen Regression:
- Die abhängige Variable in der logistischen Regression folgt der Bernoulli-Verteilung.
- Die Schätzung erfolgt durch maximale Wahrscheinlichkeit.
- Kein R-Quadrat, Modelleignung wird durch Konkordanz und KS-Statistiken berechnet.
Lineare Regression vs. Logistische Regression
Die lineare Regression liefert ein kontinuierliches Ergebnis, die logistische Regression hingegen ein konstantes Ergebnis. Ein Beispiel für einen kontinuierlichen Output sind Hauspreise und Aktienkurse. Beispiele für die diskrete Ausgabe sind die Vorhersage, ob ein Patient Krebs hat oder nicht, und die Vorhersage, ob ein Kunde abwandern wird. Die logistische Regression wird mit Hilfe der Maximum-Likelihood-Schätzung (MLE) geschätzt, während die lineare Regression in der Regel mit Hilfe der gewöhnlichen kleinsten Quadrate (OLS) geschätzt wird, die auch als Spezialfall der MLE angesehen werden kann, wenn die Fehler im Modell normal verteilt sind.
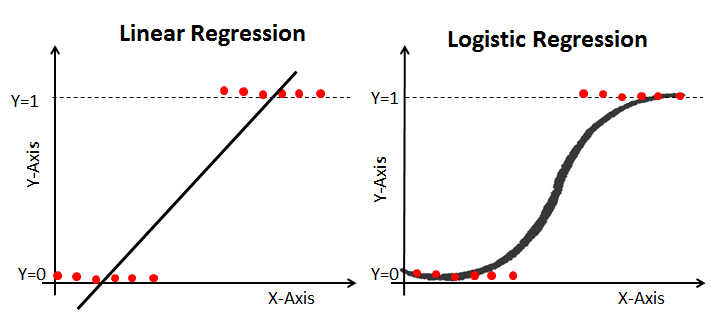
Maximum-Likelihood-Schätzung vs. Methode der kleinsten Quadrate
Die MLE ist eine Methode zur Maximierung der "Wahrscheinlichkeit", während OLS eine Methode zur Annäherung an die Distanz ist. Die Maximierung der Likelihood-Funktion bestimmt die Parameter, die am wahrscheinlichsten die beobachteten Daten ergeben. Aus statistischer Sicht setzt MLE den Mittelwert und die Varianz als Parameter bei der Bestimmung der spezifischen Parameterwerte für ein bestimmtes Modell ein. Dieser Satz von Parametern kann für die Vorhersage der Daten verwendet werden, die für eine Normalverteilung benötigt werden.
Ordentliche Kleinstquadrat-Schätzungen werden berechnet, indem eine Regressionsgerade an die gegebenen Datenpunkte angepasst wird, die die kleinste Summe der quadratischen Abweichungen (kleinster quadratischer Fehler) aufweist. Beide werden verwendet, um die Parameter eines linearen Regressionsmodells zu schätzen. MLE geht von einer gemeinsamen Wahrscheinlichkeitsmassenfunktion aus, während OLS keine stochastischen Annahmen zur Minimierung des Abstands erfordert.
Sigmoid-Funktion
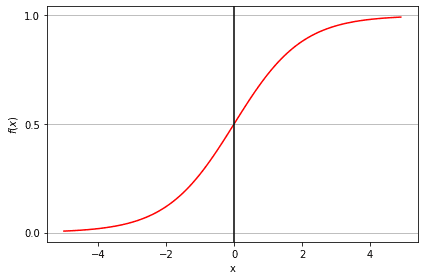
Die Sigmoidfunktion, auch logistische Funktion genannt, ergibt eine S-förmige Kurve, die jede reelle Zahl in einen Wert zwischen 0 und 1 umwandeln kann. Wenn die Kurve ins positive Unendliche geht, wird y zu 1, und wenn die Kurve ins negative Unendliche geht, wird y zu 0. Wenn die Ausgabe der Sigmoidfunktion größer als 0,5 ist, können wir das Ergebnis als 1 oder JA einstufen, und wenn sie kleiner als 0,5 ist, können wir es als 0 oder NEIN einstufen. Wenn die Ausgabe zum Beispiel 0,75 ist, können wir in Bezug auf die Wahrscheinlichkeit sagen, dass es eine 75-prozentige Chance gibt, dass ein Patient an Krebs erkrankt.

Arten der logistischen Regression
Arten der logistischen Regression:
- Binäre logistische Regression: Die Zielvariable hat nur zwei mögliche Ergebnisse: Spam oder Nicht-Spam, Krebs oder kein Krebs.
- Multinomiale logistische Regression: Die Zielvariable hat drei oder mehr nominale Kategorien, wie zum Beispiel die Vorhersage der Weinart.
- Ordinale logistische Regression: Die Zielvariable hat drei oder mehr ordinale Kategorien, z. B. eine Restaurant- oder Produktbewertung von 1 bis 5.
Modellbildung in Scikit-learn
Lass uns das Diabetes-Vorhersagemodell mithilfe eines logistischen Regressionsklassifikators erstellen.
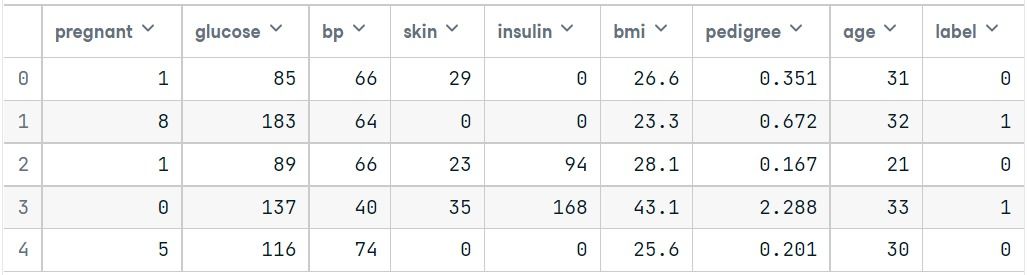
Laden wir zunächst den benötigten Pima Indian Diabetes-Datensatz mit der Read-CSV-Funktion von Pandas. Du kannst die Daten unter folgendem Link herunterladen: https://www.kaggle.com/uciml/pima-indians-diabetes-database oder einen Datensatz im DataCamp auswählen: https://www.datacamp.com/datalab/datasets. Der gebrauchsfertige Datensatz bietet dir die Möglichkeit, das Modell auf DataLab, dem kostenlosen Jupyter-Notebook von DataCamp in der Cloud, zu trainieren.
Daten laden
Wir werden die Spalten vereinfachen, indem wir col_names für Pandas read_csv() Funktion bereitstellen.
#import pandas
import pandas as pd
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("pima-indians-diabetes.csv", header=None, names=col_names)pima.head()Auswahl der Merkmale
Hier musst du die gegebenen Spalten in zwei Arten von Variablen unterteilen: abhängige (oder Zielvariable) und unabhängige Variablen (oder Merkmalsvariablen).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableDaten aufteilen
Um die Leistung des Modells zu verstehen, ist es eine gute Strategie, den Datensatz in einen Trainings- und einen Testsatz zu unterteilen.
Teilen wir den Datensatz mit der Funktion train_test_split() auf. Du musst 3 Parameter übergeben: features, target, und test_set Größe. Außerdem kannst du random_state verwenden, um Datensätze zufällig auszuwählen.
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=16)Hier wird der Datensatz in zwei Teile im Verhältnis 75:25 aufgeteilt. Das bedeutet, dass 75 % der Daten für die Modellschulung und 25 % für die Modellprüfung verwendet werden.
Modellentwicklung und Vorhersage
Importiere zunächst das Modul LogisticRegression und erstelle ein logistisches Regressionsklassifikator-Objekt, indem du die Funktion LogisticRegression() mit random_state zur Reproduzierbarkeit verwendest.
Dann passt du dein Modell mit fit() an die Trainingsmenge an und machst mit predict() eine Vorhersage für die Testmenge.
# import the class
from sklearn.linear_model import LogisticRegression
# instantiate the model (using the default parameters)
logreg = LogisticRegression(random_state=16)
# fit the model with data
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)Modellbewertung mithilfe der Konfusionsmatrix
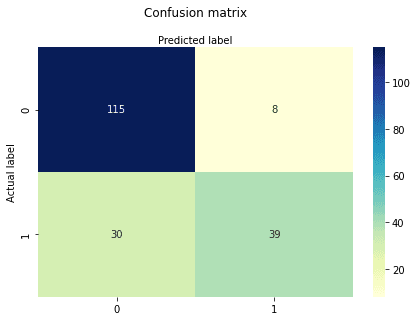
Eine Konfusionsmatrix ist eine Tabelle, die verwendet wird, um die Leistung eines Klassifizierungsmodells zu bewerten. Du kannst auch die Leistung eines Algorithmus visualisieren. Der wesentliche Teil einer Konfusionsmatrix ist die Anzahl der richtigen und falschen Vorhersagen, die klassenweise summiert werden.
# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrixarray([[115, 8],
[ 30, 39]])Hier siehst du die Verwirrungsmatrix in Form eines Array-Objekts. Die Dimension dieser Matrix ist 2*2, weil es sich bei diesem Modell um eine binäre Klassifizierung handelt. Du hast zwei Klassen 0 und 1. Diagonale Werte stehen für genaue Vorhersagen, während nicht-diagonale Elemente für ungenaue Vorhersagen stehen. In der Ausgabe sind 115 und 39 tatsächliche Vorhersagen, und 30 und 8 sind falsche Vorhersagen.
Visualisierung der Konfusionsmatrix mithilfe einer Heatmap
Lass uns die Ergebnisse des Modells in Form einer Konfusionsmatrix mit matplotlib und seaborn visualisieren.
Hier visualisierst du die Konfusionsmatrix mit der Heatmap.
# import required modules
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
class_names=[0,1] # name of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
Text(0.5,257.44,'Predicted label');Bewertungsmetriken der Konfusionsmatrix
Bewerten wir das Modell mit classification_report für Genauigkeit, Präzision und Wiedererkennung.
from sklearn.metrics import classification_report
target_names = ['without diabetes', 'with diabetes']
print(classification_report(y_test, y_pred, target_names=target_names)) precision recall f1-score support
without diabetes 0.79 0.93 0.86 123
with diabetes 0.83 0.57 0.67 69
accuracy 0.80 192
macro avg 0.81 0.75 0.77 192
weighted avg 0.81 0.80 0.79 192Nun, du hast eine Klassifizierungsrate von 80%, was als gute Genauigkeit gilt.
Präzision: Bei der Präzision geht es darum, wie genau dein Modell ist. Mit anderen Worten: Wenn ein Modell eine Vorhersage trifft, kann man sagen, wie oft es richtig ist. Wenn dein logistisches Regressionsmodell vorhersagt, dass ein Patient an Diabetes erkranken wird, dann trifft das in 73% der Fälle zu.
Rückruf: Wenn es in der Testgruppe Patienten gibt, die Diabetes haben, und dein logistisches Regressionsmodell dies in 57% der Fälle erkennen kann.
ROC-Kurve
Die Receiver-Operating-Characteristic (ROC)-Kurve ist ein Diagramm, das die wahr-positive Rate gegen die falsch-positive Rate aufträgt. Sie zeigt den Kompromiss zwischen Sensitivität und Spezifität.
y_pred_proba = logreg.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test, y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()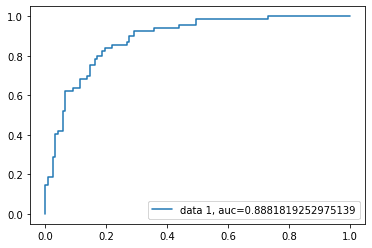
Der AUC-Wert für diesen Fall beträgt 0,88. Der AUC-Wert 1 steht für einen perfekten Klassifikator und 0,5 für einen wertlosen Klassifikator.
Der Quellcode ist auf DataLab verfügbar: Die logistische Regression in Python verstehen.
Vorteile
Da es effizient und einfach ist, erfordert es keine hohe Rechenleistung, ist einfach zu implementieren, leicht zu interpretieren und wird von vielen Datenanalysten und Wissenschaftlern genutzt. Außerdem ist keine Skalierung der Funktionen erforderlich. Die logistische Regression liefert einen Wahrscheinlichkeitswert für Beobachtungen.
Benachteiligungen
Die logistische Regression ist nicht in der Lage, eine große Anzahl von kategorialen Merkmalen/Variablen zu verarbeiten. Sie ist anfällig für eine Überanpassung. Außerdem kann sie keine nicht-linearen Probleme lösen, weshalb sie eine Transformation nicht-linearer Merkmale erfordert. Die logistische Regression funktioniert nicht gut bei unabhängigen Variablen, die nicht mit der Zielvariable korreliert sind und die einander sehr ähnlich sind oder miteinander korrelieren.
Fazit
In diesem Lernprogramm hast du viele Details über die logistische Regression gelernt. Du hast gelernt, was logistische Regression ist, wie man entsprechende Modelle erstellt, wie man Ergebnisse visualisiert und einige theoretische Hintergrundinformationen. Außerdem hast du einige grundlegende Konzepte wie die Sigmoidfunktion, maximale Wahrscheinlichkeit, Konfusionsmatrix und ROC-Kurve behandelt.
Wir hoffen, dass du jetzt die logistische Regression nutzen kannst, um deine eigenen Datensätze zu analysieren. Danke fürs Lesen dieses Tutorials!
Wenn du mehr über die logistische Regression erfahren möchtest, besuche den Kurs " Maschinelles Lernen mit scikit-learn " von DataCamp. Du kannst deine Reise zum Ingenieur für maschinelles Lernen auch beginnen, indem du dich für den Karrierepfad Machine Learning Scientist with Python anmeldest.