El Algoritmo A*: Guía completa

Los algoritmos de recorrido de grafos son fundamentales para muchas aplicaciones informáticas, desde el desarrollo de juegos hasta la robótica. Estos algoritmos están diseñados para explorar y navegar por grafos, que son estructuras de datos compuestas por nodos (vértices) y aristas. Entre estos algoritmos, el algoritmo A* destaca como un enfoque especialmente eficaz y versátil para encontrar trayectorias óptimas.

El algoritmo A* es un algoritmo de búsqueda informada, lo que significa que aprovecha una función heurística para guiar su búsqueda hacia el objetivo. Esta función heurística estima el coste de alcanzar el objetivo desde un nodo determinado, lo que permite al algoritmo dar prioridad a los caminos prometedores y evitar explorar los innecesarios.

En este artículo, veremos los conceptos clave del algoritmo A*, su implementación en Python, sus aplicaciones y sus ventajas y limitaciones.

Para aprender más sobre la programación en Python, consulta nuestro Curso de Introducción a Python para Desarrolladores curso.

¿Qué es el Algoritmo A*?

El algoritmo A* es un algoritmo potente y ampliamente utilizado para recorrer grafos y encontrar caminos. Encuentra el camino más corto entre un nodo inicial y un nodo objetivo en un grafo ponderado. 

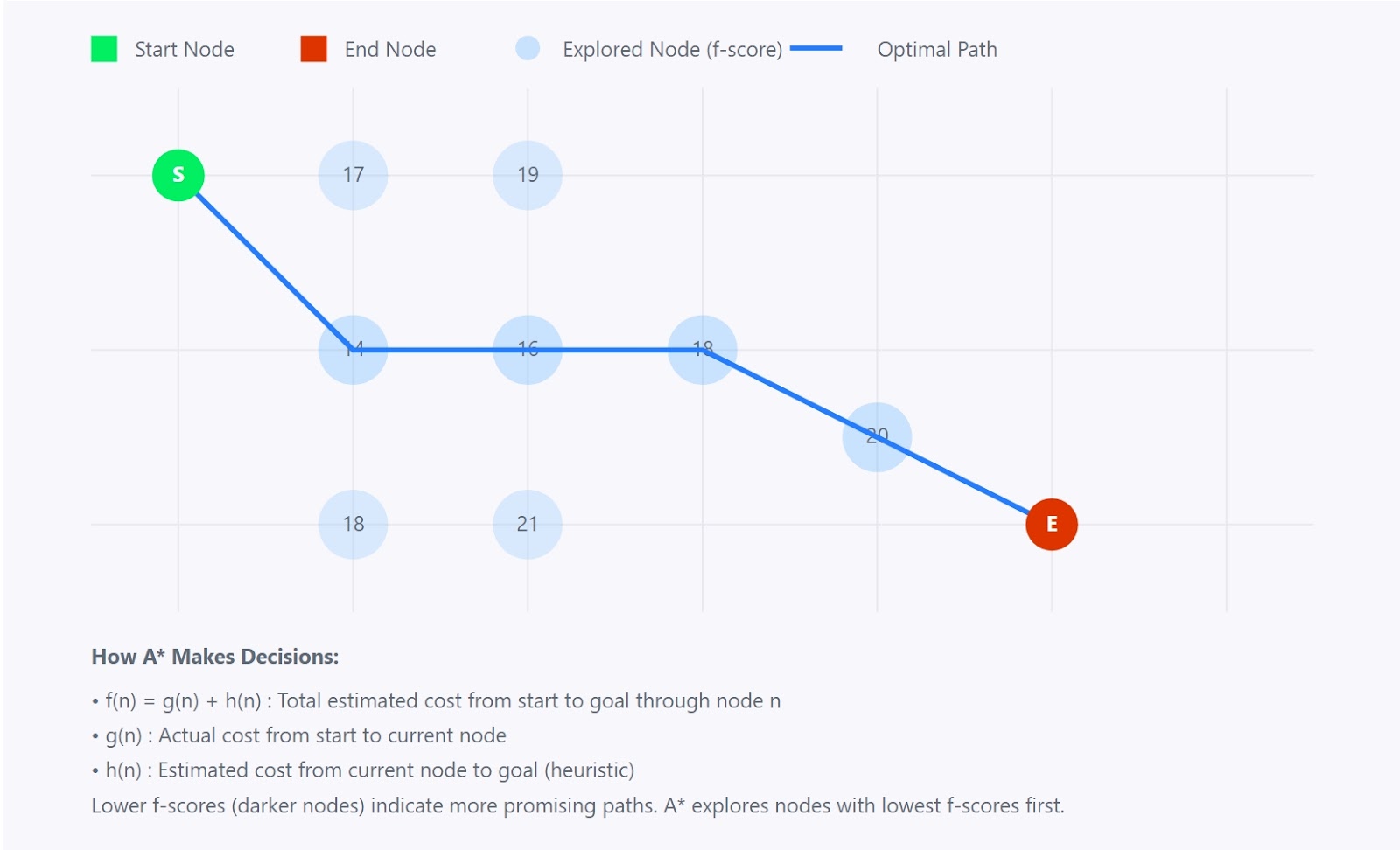
Algoritmo A

¿Cómo funciona el algoritmo A*?

El algoritmo A* combina los mejores aspectos de otros dos algoritmos:

1. Algoritmo de Dijkstra: Este algoritmo encuentra el camino más corto a todos los nodos desde un único nodo origen.
2. Búsqueda codiciosa del mejor primero: Este algoritmo explora el nodo que parece estar más cerca del objetivo, basándose en una función heurística.

Imagina que intentas encontrar en un mapa la ruta más corta entre dos ciudades. Mientras que el algoritmo de Dijkstra exploraría en todas direcciones y la Búsqueda Mejor Primero podría dirigirse directamente hacia el destino (omitiendo potencialmente atajos), A* hace algo más inteligente. Considera ambas cosas:

• La distancia ya recorrida desde el inicio
• Una estimación inteligente de la distancia restante hasta la meta

Esta combinación ayuda a A* a tomar decisiones informadas sobre qué camino explorar a continuación, haciéndolo a la vez eficiente y preciso.

Componentes clave

Para entender el algoritmo A*, tienes que estar familiarizado con estos conceptos fundamentales:

• Nodos: Puntos en tu gráfico (como las intersecciones en un mapa)
• Bordes: Conexiones entre nodos (como carreteras que conectan intersecciones)
• Coste de la ruta: El coste real de pasar de un nodo a otro
• Heurística: Un coste estimado desde cualquier nodo hasta el objetivo
• Espacio de búsqueda: La colección de todos los posibles caminos a explorar

En la siguiente sección, profundizaremos en estos conceptos y veremos cómo los utiliza A* para encontrar rutas óptimas.

Conceptos clave de la búsqueda A*

La eficacia del algoritmo A* procede de su evaluación inteligente de trayectorias mediante tres componentes clave: g(n), h(n) y f(n). Estos componentes trabajan juntos para guiar el proceso de búsqueda hacia los caminos más prometedores.

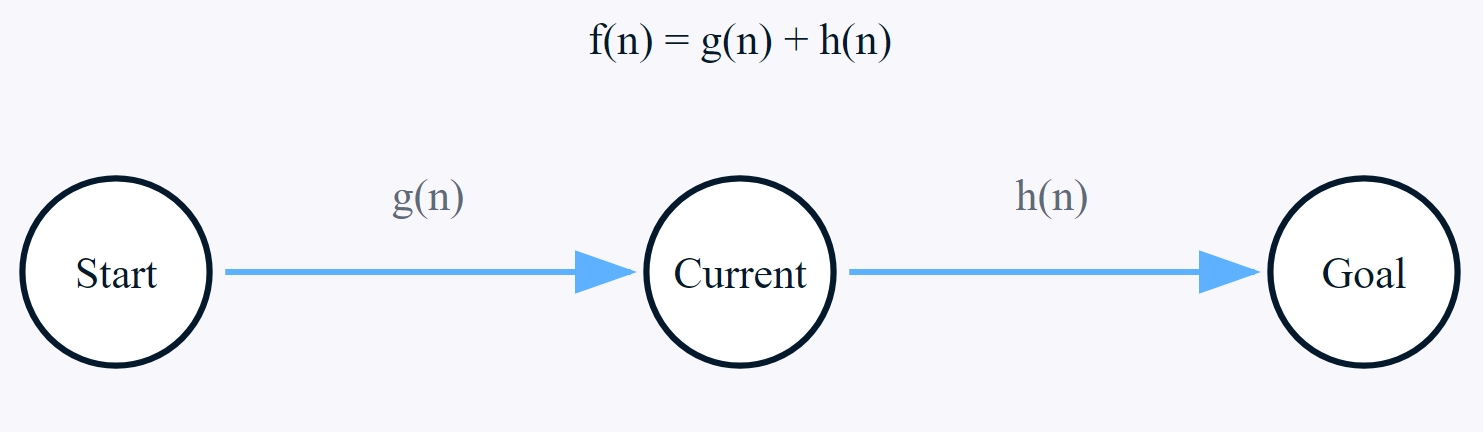
Algoritmo A* Función de coste

Comprender las funciones de coste

Coste del camino g(n)

La función de coste del camino g(n) representa la distancia exacta y conocida desde el nodo inicial de partida hasta la posición actual en nuestra búsqueda. A diferencia de los valores estimados, este coste es preciso y se calcula sumando todos los pesos individuales de las aristas que se han recorrido a lo largo del camino elegido. 

Matemáticamente, para una trayectoria a través de los nodos n0(nodo inicial) a nk​ (nodo actual), podemos expresar g(n) como

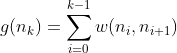
Dónde:

• w(n_i,n_i+1) representa el peso de la arista que conecta el nodo ni al nodo n_i+1​.

A medida que avanzamos por el gráfico, este valor se acumula, dándonos una medida clara de los recursos reales (ya sea distancia, tiempo o cualquier otra métrica) que hemos gastado para llegar a nuestra posición actual.

Función heurística h(n)

La función heurística h(n) proporciona un coste estimado desde el nodo actual hasta el nodo objetivo, actuando como "conjetura informada" del algoritmo sobre el camino restante. 

Matemáticamente, para cualquier nodo n dado, la estimación heurística debe satisfacer la condición h(n)≤h*(n) donde h*(n) es el coste real del objetivo, lo que lo hace admisible al no sobrestimar nunca el coste real.

En los problemas basados en cuadrículas o en mapas, las funciones heurísticas comunes incluyen la distancia Manhattan y distancia euclidiana. Para las coordenadas (x₁,y₁) del nodo actual y (x₂,y₂) del nodo meta, estas distancias se calculan como

Distancia a Manhattan

Distancia euclidiana

Coste total estimado f(n)

El coste total estimado f(n) es la piedra angular del proceso de toma de decisiones del algoritmo A*, que combina tanto el coste real de la ruta como la estimación heurística para evaluar el potencial de cada nodo. Para cualquier nodo n, este coste se calcula como

Dónde:

• g(n) representa el coste real desde el inicio hasta el nodo actual,
• h(n) representa el coste estimado desde el nodo actual hasta el objetivo.

El algoritmo algoritmo utiliza este valor combinado para elegir estratégicamente qué nodo explorar a continuación, seleccionando siempre el nodo con la menor f(n) más bajo de la lista abierta, garantizando así un equilibrio óptimo entre los costes conocidos y las distancias restantes estimadas.

Gestionar listas de nodos

El algoritmo A* mantiene dos listas esenciales

Lista abierta:

• Contiene nodos que deben evaluarse
• Ordenados por valor de f(n) (primero el más bajo)
• Se añaden nuevos nodos a medida que se descubren

Lista cerrada:

• Contiene nodos ya evaluados
• Ayuda a evitar la reevaluación de nodos
• Se utiliza para reconstruir la trayectoria final

El algoritmo selecciona continuamente el nodo con el valor más bajo de f(n) más bajo de la lista abierta, lo evalúa y lo mueve a la lista cerrada hasta que llega al nodo meta o determina que no existe ningún camino.

Algoritmo de búsqueda A* Pseudocódigo

Ahora que conocemos los componentes fundamentales de A*, veamos cómo se combinan en la práctica. La implementación del algoritmo puede descomponerse en pasos claros y lógicos que transforman estos conceptos en una solución de búsqueda de caminos que funciona.

He aquí cómo funciona el algoritmo, paso a paso:

function A_Star(start, goal):
    // Initialize open and closed lists
    openList = [start]          // Nodes to be evaluated
    closedList = []            // Nodes already evaluated
    
    // Initialize node properties
    start.g = 0                // Cost from start to start is 0
    start.h = heuristic(start, goal)  // Estimate to goal
    start.f = start.g + start.h       // Total estimated cost
    start.parent = null              // For path reconstruction
    while openList is not empty:
        // Get node with lowest f value - implement using a priority queue
       // for faster retrieval of the best node
        current = node in openList with lowest f value
        
        // Check if we've reached the goal
        if current = goal:
            return reconstruct_path(current)
            
        // Move current node from open to closed list
        remove current from openList
        add current to closedList
        
        // Check all neighboring nodes
        for each neighbor of current:
            if neighbor in closedList:
                continue  // Skip already evaluated nodes
                
            // Calculate tentative g score
            tentative_g = current.g + distance(current, neighbor)
            
            if neighbor not in openList:
                add neighbor to openList
            else if tentative_g >= neighbor.g:
                continue  // This path is not better
                
            // This path is the best so far
            neighbor.parent = current
            neighbor.g = tentative_g
            neighbor.h = heuristic(neighbor, goal)
            neighbor.f = neighbor.g + neighbor.h
    
    return failure  // No path exists
function reconstruct_path(current):
    path = []
    while current is not null:
        add current to beginning of path
        current = current.parent
    return path

Vamos a desglosar cada componente de esta aplicación:

Fase de inicialización

El algoritmo comienza estableciendo dos listas esenciales:

• La lista abierta comienza sólo con el nodo inicial
• La lista cerrada empieza vacía

Cada nodo almacena cuatro informaciones críticas:

• g: El coste real desde el nodo inicial
• h: El coste estimado para el objetivo
• f: La suma de g y h
• padre: Referencia al nodo anterior (para reconstruir la ruta)

Bucle principal

El núcleo de A* es su bucle principal, que continúa hasta que

• Se alcanza el objetivo (éxito)
• La lista abierta queda vacía (fallo - no existe ninguna ruta)

Durante cada iteración, el algoritmo:

1. Selecciona el nodo más prometedor (valor f más bajo) de la lista abierta
2. Lo mueve a la lista cerrada
3. Examina todos los nodos vecinos

Evaluación de vecinos

Para cada vecino, el algoritmo

• Omite los nodos que ya están en la lista cerrada
• Calcula una puntuación g provisional
• Actualiza los valores de los nodos si se encuentra un camino mejor
• Añade nuevos nodos a la lista abierta

Reconstrucción del camino

Una vez alcanzado el objetivo, el algoritmo trabaja hacia atrás a través de las referencias padre para construir el camino óptimo desde el inicio hasta el objetivo.

Este enfoque sistemático garantiza que A* siempre encontrará el camino óptimo si:

1. La función heurística es admisible (nunca sobreestima)
2. Existe realmente un camino entre los nodos inicial y meta

En la siguiente sección, traduciremos este pseudocódigo en una implementación práctica en Python, completa con visualizaciones que te ayudarán a entender cómo explora el algoritmo el espacio de búsqueda.

Implementación en Python del algoritmo A*

Ahora que entendemos la teoría y el pseudocódigo, vamos a implementar A* en Python. Crearemos una aplicación práctica que podrás utilizar como base para tus propios proyectos. Para concretarlo, implementaremos el algoritmo en una cuadrícula 2D, un escenario habitual en juegos y aplicaciones robóticas.

Paso 1: Funciones esenciales e importaciones

Primero importamos las bibliotecas necesarias y creamos una estructura de nodos que almacenará información sobre la posición y la trayectoria de cada punto de nuestro espacio de búsqueda.

from typing import List, Tuple, Dict, Set
import numpy as np
import heapq
from math import sqrt
def create_node(position: Tuple[int, int], g: float = float('inf'), 
                h: float = 0.0, parent: Dict = None) -> Dict:
    """
    Create a node for the A* algorithm.
    
    Args:
        position: (x, y) coordinates of the node
        g: Cost from start to this node (default: infinity)
        h: Estimated cost from this node to goal (default: 0)
        parent: Parent node (default: None)
    
    Returns:
        Dictionary containing node information
    """
    return {
        'position': position,
        'g': g,
        'h': h,
        'f': g + h,
        'parent': parent
    }

Paso 2: Funciones auxiliares

Para apoyar nuestro algoritmo de búsqueda de trayectorias, crearemos varias funciones de ayuda. En primer lugar, implementaremos una función para calcular distancias entre puntos utilizando la distancia euclídea.

Después, añadiremos una función para encontrar posiciones vecinas válidas en nuestra cuadrícula, comprobando cuidadosamente los límites y los obstáculos. Por último, crearemos una función que nos ayude a reconstruir el camino una vez que hayamos encontrado nuestro objetivo.

def calculate_heuristic(pos1: Tuple[int, int], pos2: Tuple[int, int]) -> float:
    """
    Calculate the estimated distance between two points using Euclidean distance.
    """
    x1, y1 = pos1
    x2, y2 = pos2
    return sqrt((x2 - x1)**2 + (y2 - y1)**2)
def get_valid_neighbors(grid: np.ndarray, position: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Get all valid neighboring positions in the grid.
    
    Args:
        grid: 2D numpy array where 0 represents walkable cells and 1 represents obstacles
        position: Current position (x, y)
    
    Returns:
        List of valid neighboring positions
    """
    x, y = position
    rows, cols = grid.shape
    
    # All possible moves (including diagonals)
    possible_moves = [
        (x+1, y), (x-1, y),    # Right, Left
        (x, y+1), (x, y-1),    # Up, Down
        (x+1, y+1), (x-1, y-1),  # Diagonal moves
        (x+1, y-1), (x-1, y+1)
    ]
    
    return [
        (nx, ny) for nx, ny in possible_moves
        if 0 <= nx < rows and 0 <= ny < cols  # Within grid bounds
        and grid[nx, ny] == 0                # Not an obstacle
    ]
def reconstruct_path(goal_node: Dict) -> List[Tuple[int, int]]:
    """
    Reconstruct the path from goal to start by following parent pointers.
    """
    path = []
    current = goal_node
    
    while current is not None:
        path.append(current['position'])
        current = current['parent']
        
    return path[::-1]  # Reverse to get path from start to goal

Paso 3: Implementación principal del algoritmo A

Ahora vamos a poner en práctica nuestro algoritmo. Utilizaremos una cola de prioridad para asegurarnos de que siempre exploramos primero los caminos más prometedores. 

Nuestro algoritmo mantendrá dos conjuntos: un conjunto abierto para los nodos que aún tenemos que explorar y un conjunto cerrado para los nodos que ya hemos comprobado. 

A medida que exploremos la malla, actualizaremos continuamente los costes de las rutas cada vez que encontremos rutas mejores, hasta que alcancemos nuestro objetivo.

def find_path(grid: np.ndarray, start: Tuple[int, int], 
              goal: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Find the optimal path using A* algorithm.
    
    Args:
        grid: 2D numpy array (0 = free space, 1 = obstacle)
        start: Starting position (x, y)
        goal: Goal position (x, y)
    
    Returns:
        List of positions representing the optimal path
    """
    # Initialize start node
    start_node = create_node(
        position=start,
        g=0,
        h=calculate_heuristic(start, goal)
    )
    
    # Initialize open and closed sets
    open_list = [(start_node['f'], start)]  # Priority queue
    open_dict = {start: start_node}         # For quick node lookup
    closed_set = set()                      # Explored nodes
    
    while open_list:
        # Get node with lowest f value
        _, current_pos = heapq.heappop(open_list)
        current_node = open_dict[current_pos]
        
        # Check if we've reached the goal
        if current_pos == goal:
            return reconstruct_path(current_node)
            
        closed_set.add(current_pos)
        
        # Explore neighbors
        for neighbor_pos in get_valid_neighbors(grid, current_pos):
            # Skip if already explored
            if neighbor_pos in closed_set:
                continue
                
            # Calculate new path cost
            tentative_g = current_node['g'] + calculate_heuristic(current_pos, neighbor_pos)
            
            # Create or update neighbor
            if neighbor_pos not in open_dict:
                neighbor = create_node(
                    position=neighbor_pos,
                    g=tentative_g,
                    h=calculate_heuristic(neighbor_pos, goal),
                    parent=current_node
                )
                heapq.heappush(open_list, (neighbor['f'], neighbor_pos))
                open_dict[neighbor_pos] = neighbor
            elif tentative_g < open_dict[neighbor_pos]['g']:
                # Found a better path to the neighbor
                neighbor = open_dict[neighbor_pos]
                neighbor['g'] = tentative_g
                neighbor['f'] = tentative_g + neighbor['h']
                neighbor['parent'] = current_node
    
    return []  # No path found

Paso 4: Visualización

Ahora, vamos a crear una función de visualización. Esto nos mostrará la disposición de nuestra cuadrícula con los obstáculos, dibujará nuestra trayectoria óptima calculada y marcará claramente nuestras posiciones de inicio y meta.

import matplotlib.pyplot as plt
def visualize_path(grid: np.ndarray, path: List[Tuple[int, int]]):
    """
    Visualize the grid and found path.
    """
    plt.figure(figsize=(10, 10))
    plt.imshow(grid, cmap='binary')
    
    if path:
        path = np.array(path)
        plt.plot(path[:, 1], path[:, 0], 'b-', linewidth=3, label='Path')
        plt.plot(path[0, 1], path[0, 0], 'go', markersize=15, label='Start')
        plt.plot(path[-1, 1], path[-1, 0], 'ro', markersize=15, label='Goal')
    
    plt.grid(True)
    plt.legend(fontsize=12)
    plt.title("A* Pathfinding Result")
    plt.show()

Ejemplo de uso

A continuación te explicamos cómo utilizar la aplicación:

# Create a sample grid
grid = np.zeros((20, 20))  # 20x20 grid, all free space initially
# Add some obstacles
grid[5:15, 10] = 1  # Vertical wall
grid[5, 5:15] = 1   # Horizontal wall
# Define start and goal positions
start_pos = (2, 2)
goal_pos = (18, 18)
# Find the path
path = find_path(grid, start_pos, goal_pos)
if path:
    print(f"Path found with {len(path)} steps!")
    visualize_path(grid, path)
else:
    print("No path found!")

Salida

¡Camino encontrado con 22 pasos!

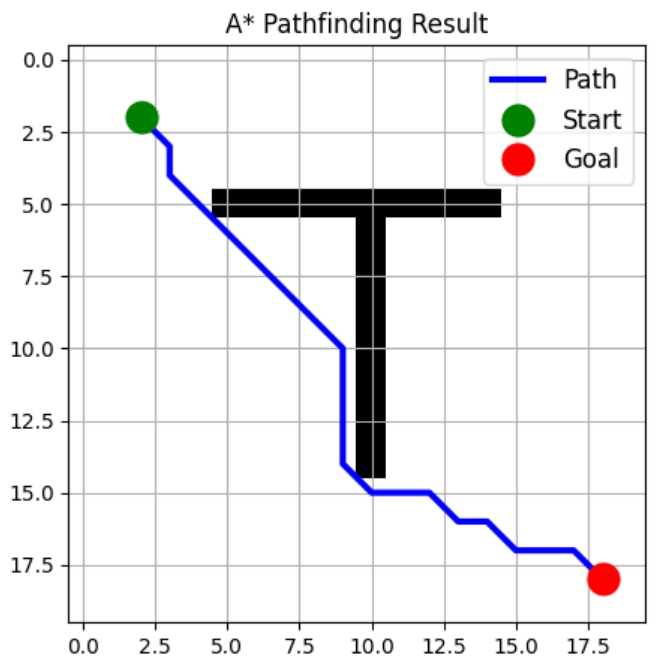
Esta aplicación es eficaz y ampliable. Puedes modificarlo fácilmente:

• Utilizar diferentes funciones heurísticas
• Soporta diferentes tipos de movimiento
• Manejar rejillas lastradas
• Incluir limitaciones adicionales

En la siguiente sección, veremos algunas aplicaciones prácticas de este algoritmo y veremos cómo se utiliza en situaciones reales.

Aplicaciones del algoritmo de búsqueda A*

La eficacia y flexibilidad del algoritmo A* lo hacen valioso en numerosos ámbitos. Éstas son las áreas clave en las que destaca:

1. Videojuegos y entretenimiento

El algoritmo de búsqueda A* se utiliza mucho en el desarrollo de videojuegos por su capacidad de búsqueda de trayectorias óptimas. Mejora la experiencia del jugador al permitir un movimiento del personaje más realista y sensible.

• Trayectoria del personaje en los juegos de estrategia: A* ayuda a los personajes a encontrar el camino más corto o seguro hacia un objetivo, algo crucial en los juegos de estrategia en tiempo real (RTS) en los que las unidades tienen que sortear obstáculos y enemigos con eficacia.
• Movimiento de los PNJ en entornos de mundo abierto: Los personajes no jugables (PNJ) utilizan A* para navegar por mundos de juego grandes y dinámicos, lo que les permite alcanzar objetivos evitando obstáculos y a otros personajes.
• Planificación táctica en tiempo real en escenarios de combate: A* se utiliza para calcular el movimiento y la posición eficaces de las unidades durante el combate, garantizando que los personajes puedan llegar rápidamente a los lugares ventajosos y, al mismo tiempo, evitar el peligro.
• Resolución de laberintos en juegos de puzzle: A* es un algoritmo eficaz para recorrer laberintos complejos, que ofrece a los jugadores un reto atractivo al potenciar a los oponentes dinámicos para resolver laberintos o proporcionar pistas.

2. Sistemas de navegación

A* se utiliza mucho en los sistemas de navegación para optimizar las rutas, teniendo en cuenta diversos factores como la distancia y los posibles obstáculos.

• Planificación de rutas en aplicaciones GPS: A* encuentra la ruta más corta y rápida entre dos puntos, lo que lo convierte en un componente esencial del software GPS utilizado por millones de personas en todo el mundo.
• Servicios de navegación adaptados al tráfico: En las modernas aplicaciones de navegación, la A* se combina con datos de tráfico en tiempo real para sugerir la mejor ruta, minimizando el tiempo de viaje y evitando las carreteras congestionadas.
• Optimización de rutas de transporte público: A* puede ayudar a encontrar rutas óptimas que incorporen múltiples modos de transporte público, garantizando que los usuarios hagan transbordos eficientes.
• Sistemas de navegación en interiores: A* también se utiliza en la navegación en interiores, como en aeropuertos o grandes centros comerciales, donde ayuda a guiar a los usuarios por entornos complejos con múltiples niveles y obstáculos.

3. Robótica y automatización

El algoritmo A* es crucial para la robótica, donde el movimiento eficiente es esencial para la productividad y la seguridad.

• Planificación autónoma de la trayectoria del vehículo: Los coches autoconducidos utilizan A* para navegar por las carreteras, tomando decisiones en tiempo real sobre cómo desplazarse del punto A al punto B evitando colisiones y respetando las normas de tráfico.
• Navegación de robots de almacén: En los almacenes automatizados, los robots confían en A* para navegar eficazmente entre las estanterías de almacenamiento para recoger y colocar artículos, minimizando los retrasos y evitando colisiones con otros robots.
• Optimización de la trayectoria de vuelo de los drones: A* ayuda a los drones a planificar trayectorias de vuelo eficientes, ya sea para entregas, inspecciones o uso recreativo, asegurándose de que evitan obstáculos y siguen rutas óptimas.
• Planificación del movimiento del robot de fabricación: En las fábricas, A* se utiliza para garantizar que los robots puedan moverse sin problemas entre los puestos de trabajo, evitando colisiones con otras máquinas y manteniendo la productividad.

4. Sistemas de red

A* también se aplica en la optimización de las operaciones de red, donde la eficiencia en la utilización de los recursos y el encaminamiento es primordial.

• Enrutamiento de paquetes de red: A* se utiliza para determinar la ruta más eficiente para que los paquetes de datos viajen a través de una red, garantizando una latencia mínima y una alta fiabilidad.
• Asignación de recursos en sistemas distribuidos: A* ayuda a optimizar la asignación de recursos, lo que permite a los sistemas distribuidos asignar eficazmente las tareas entre varios nodos minimizando la sobrecarga.
• Diseño de la trayectoria de la placa de circuito: Al diseñar placas de circuitos impresos (PCB), A* puede utilizarse para determinar las trayectorias óptimas de las trazas eléctricas, garantizando interferencias mínimas y un trazado eficaz.
• Optimización del encaminamiento de los cables de red: A* se emplea en el diseño de infraestructuras físicas de red, encontrando las rutas más eficaces para que los cables minimicen el coste y maximicen el rendimiento.

Lo que hace que A* sea especialmente valioso es su adaptabilidad mediante funciones heurísticas personalizadas, que permiten optimizar diferentes métricas como la distancia, el tiempo o el consumo de energía.

En la siguiente sección, veremos algunos retos comunes y técnicas de optimización para implantar A* con eficacia.

Retos comunes y técnicas de optimización

Aunque A* es potente, su aplicación efectiva requiere abordar varios retos comunes. El obstáculo más importante al que se enfrentan los desarrolladores es la gestión eficaz de los recursos, sobre todo cuando se trata de grandes espacios de búsqueda.

Los principales retos incluyen:

• Consumo de memoria en grafos grandes
• Cuellos de botella de rendimiento con heurísticas complejas
• Manejo de las situaciones de desempate
• Equilibrio entre precisión y velocidad de cálculo

Afortunadamente, existen varias estrategias de optimización eficaces para afrontar estos retos:

• Para la gestión de la memoria, céntrate en estructuras de datos
• Utilizar montones binarios para la lista abierta en lugar de matrices
• Implementar una tabla hash para búsquedas más rápidas en listas cerradas
• Borra los datos innecesarios del nodo después del procesamiento

Cuando el rendimiento es fundamental, ten en cuenta estas mejoras de velocidad:

• Simplifica los cálculos heurísticos siempre que sea posible
• Utiliza la aritmética de enteros en lugar de la de coma flotante
• Implementar la búsqueda jerárquica de rutas para mapas grandes

Un enfoque especialmente eficaz para espacios grandes es la búsqueda bilateral: buscar desde el inicio y desde la meta simultáneamente. Además, cuando trabajes con la búsqueda de rutas basada en cuadrículas, puedes mejorar significativamente el rendimiento calculando previamente los valores heurísticos o utilizando tablas de consulta.

Recuerda que debes elegir las técnicas de optimización en función de tus requisitos y limitaciones específicos. La clave está en encontrar el equilibrio adecuado entre el uso de memoria y la velocidad de cálculo para tu aplicación.

Conclusión

El algoritmo A* es una herramienta fundamental en los problemas de búsqueda de caminos y recorrido de grafos. A través de esta guía, hemos visto sus conceptos básicos, implementado una solución práctica en Python y examinado sus diversas aplicaciones. La fuerza del algoritmo reside en su equilibrio entre precisión y eficacia, lo que lo hace inestimable en diversos ámbitos, desde los juegos a la robótica.

Aunque implantar A* conlleva sus retos, las técnicas de optimización que hemos comentado pueden ayudarte a crear soluciones eficientes. Si desarrollas juegos, planificas las trayectorias de un robot o resuelves problemas de enrutamiento, comprender el algoritmo A* te proporciona un potente enfoque para encontrar trayectorias óptimas en tus aplicaciones

Construir algoritmos tan sofisticados requiere una base sólida en conceptos y buenas prácticas de programación en Python. ¿Quieres reforzar tus fundamentos de Python y enfrentarte a algoritmos más avanzados como A*? 

Lleva tus habilidades de programación al siguiente nivel con nuestro Curso Python Intermedio para Desarrolladores donde dominarás las funciones personalizadas, explorarás módulos esenciales y crearás aplicaciones sofisticadas.