The A* Algorithm: A Complete Guide

Graph traversal algorithms are fundamental to many computer science applications, from game development to robotics. These algorithms are designed to explore and navigate through graphs, which are data structures composed of nodes (vertices) and edges. Among these algorithms, the A* algorithm stands out as a particularly efficient and versatile approach for finding optimal paths.

The A* algorithm is an informed search algorithm, meaning it leverages a heuristic function to guide its search towards the goal. This heuristic function estimates the cost of reaching the goal from a given node, allowing the algorithm to prioritize promising paths and avoid exploring unnecessary ones.

In this article, we'll look at the key concepts of the A* algorithm, its implementation in Python, its applications, and its advantages and limitations.

To learn more about Python programming, check out our Introduction to Python for Developers Course course.    

What is the A* Algorithm?

The A* algorithm is a powerful and widely used graph traversal and path finding algorithm. It finds the shortest path between a starting node and a goal node in a weighted graph. 

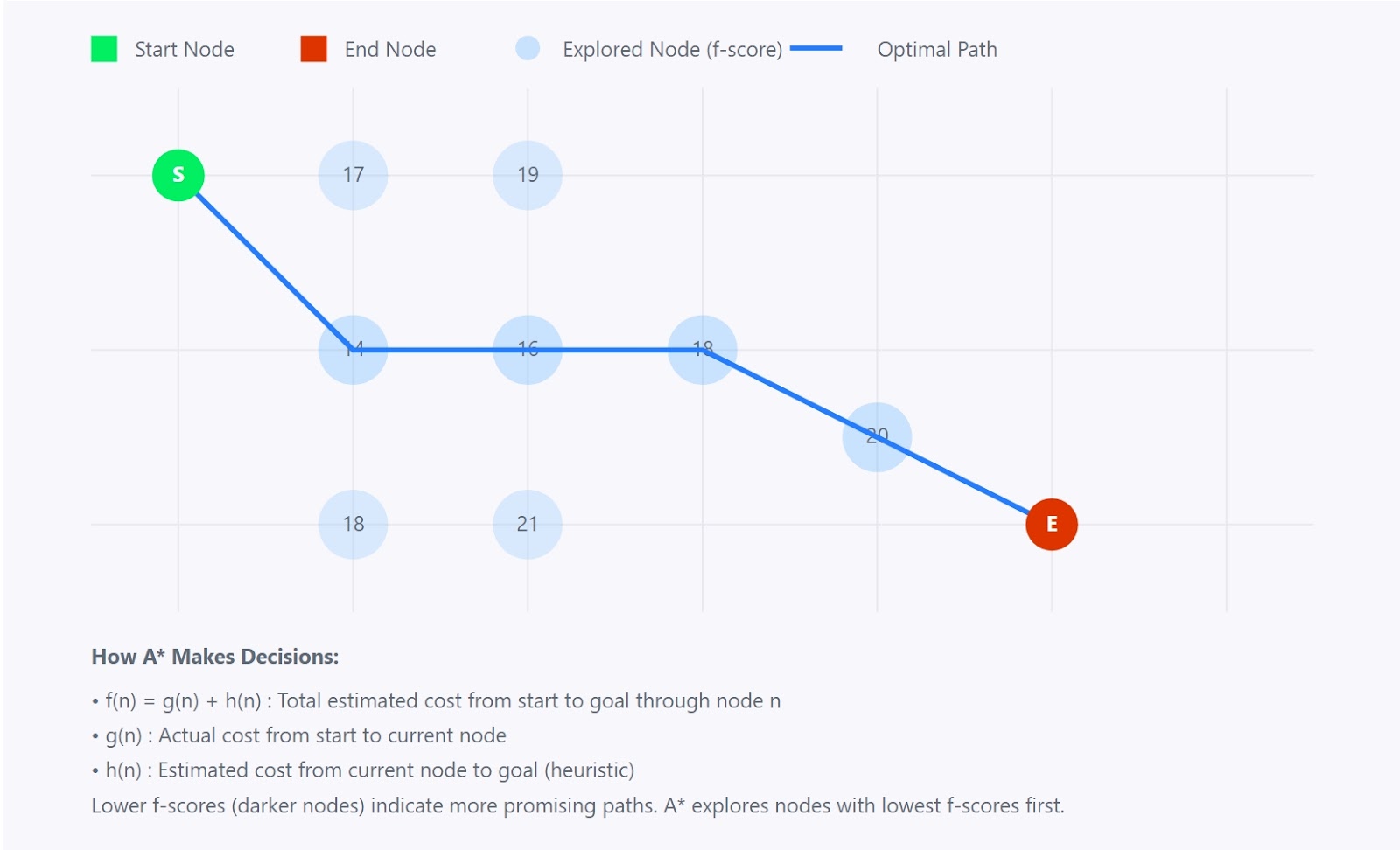
A* algorithm

How Does the A* Algorithm Work?

The A* algorithm combines the best aspects of two other algorithms:

1. Dijkstra's Algorithm: This algorithm finds the shortest path to all nodes from a single source node.
2. Greedy Best-First Search: This algorithm explores the node that appears to be closest to the goal, based on a heuristic function.

Imagine you're trying to find the shortest route between two cities on a map. While Dijkstra's algorithm would explore in all directions and Best-First Search might head straight toward the destination (potentially missing shortcuts), A* does something cleverer. It considers both:

• The distance already traveled from the start
• A smart estimate of the remaining distance to the goal

This combination helps A* make informed decisions about which path to explore next, making it both efficient and accurate.

Key components

To understand A* algorithm, you need to be familiar with these fundamental concepts:

• Nodes: Points in your graph (like intersections on a map)
• Edges: Connections between nodes (like roads connecting intersections)
• Path Cost: The actual cost of moving from one node to another
• Heuristic: An estimated cost from any node to the goal
• Search Space: The collection of all possible paths to explore

In the next section, we'll look deeper into these concepts and see how A* uses them to find optimal paths.

Key Concepts in A* Search

The A* algorithm's efficiency comes from its smart evaluation of paths using three key components: g(n), h(n), and f(n). These components work together to guide the search process toward the most promising paths.

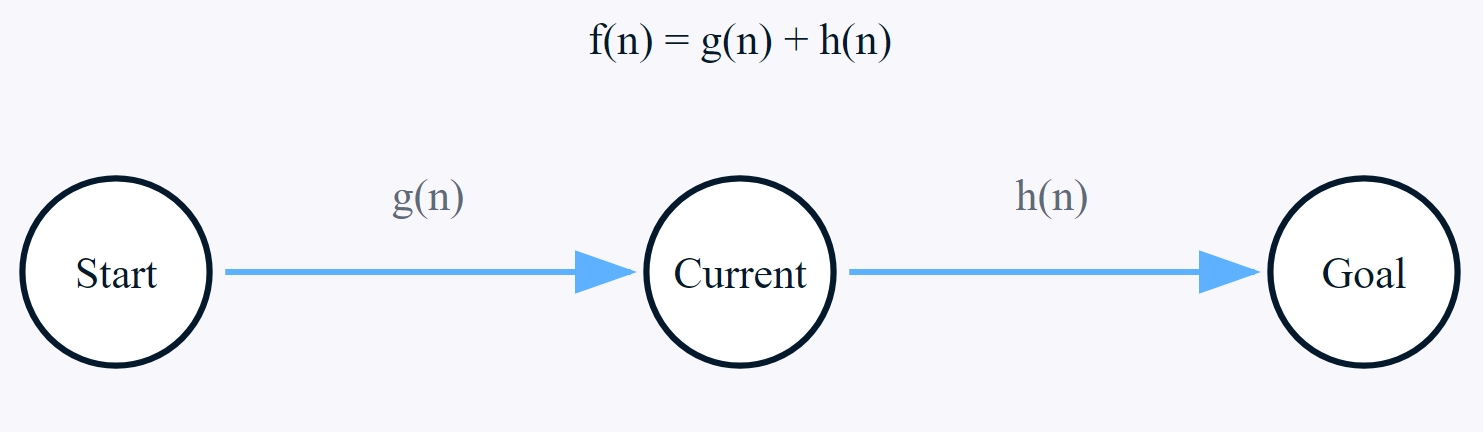
A* algorithm Cost Function

Understanding the cost functions

Path cost g(n)

The path cost function g(n) represents the exact, known distance from the initial starting node to the current position in our search. Unlike estimated values, this cost is precise and calculated by adding up all the individual edge weights that have been traversed along our chosen path. 

Mathematically, for a path through nodes n0(start node) to nk​ (current node), we can express g(n) as:

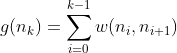
Where:

• w(n_i,n_i+1) represents the weight of the edge connecting node ni to node n_i+1​.

As we move through the graph, this value accumulates, giving us a clear measure of the actual resources (whether that's distance, time, or any other metric) we've expended to reach our current position.

Heuristic function h(n)

The heuristic function h(n) provides an estimated cost from the current node to the goal node, acting as the algorithm's "informed guess" about the remaining path. 

Mathematically, for any given node n, the heuristic estimate must satisfy the condition h(n)≤h*(n) , where h*(n) is the actual cost to the goal, making it admissible by never overestimating the true cost.

In grid-based or map-like problems, common heuristic functions include the Manhattan distance and Euclidean distance. For coordinates (x₁,y₁) of the current node and (x₂,y₂) of the goal node, these distances are calculated as:

Manhattan distance

Euclidean distance

Total estimated cost f(n)

The total estimated cost f(n) is the cornerstone of A* algorithm's decision-making process, combining both the actual path cost and the heuristic estimate to evaluate each node's potential. For any node n, this cost is calculated as:

Where:

• g(n) represents the actual cost from the start to the current node,
• h(n) represents the estimated cost from the current node to the goal. 

The algorithm uses this combined value to strategically choose which node to explore next, always selecting the node with the lowest f(n) value from the open list, thus ensuring an optimal balance between known costs and estimated remaining distances.

Managing node lists

The A* algorithm maintains two essential lists

Open list:

• Contains nodes that need to be evaluated
• Sorted by f(n) value (lowest first)
• New nodes are added as they're discovered

Closed list:

• Contains already evaluated nodes
• Helps avoid re-evaluating nodes
• Used to reconstruct the final path

The algorithm continually selects the node with the lowest f(n) value from the open list, evaluates it, and moves it to the closed list until it reaches the goal node or determines no path exists.

A* Search Algorithm Pseudocode

Now that we understand the fundamental components of A*, let's see how they come together in practice. The algorithm's implementation can be broken down into clear, logical steps that transform these concepts into a working path finding solution.

Here's how the algorithm works, step by step:

function A_Star(start, goal):
    // Initialize open and closed lists
    openList = [start]          // Nodes to be evaluated
    closedList = []            // Nodes already evaluated
    
    // Initialize node properties
    start.g = 0                // Cost from start to start is 0
    start.h = heuristic(start, goal)  // Estimate to goal
    start.f = start.g + start.h       // Total estimated cost
    start.parent = null              // For path reconstruction
    while openList is not empty:
        // Get node with lowest f value - implement using a priority queue
       // for faster retrieval of the best node
        current = node in openList with lowest f value
        
        // Check if we've reached the goal
        if current = goal:
            return reconstruct_path(current)
            
        // Move current node from open to closed list
        remove current from openList
        add current to closedList
        
        // Check all neighboring nodes
        for each neighbor of current:
            if neighbor in closedList:
                continue  // Skip already evaluated nodes
                
            // Calculate tentative g score
            tentative_g = current.g + distance(current, neighbor)
            
            if neighbor not in openList:
                add neighbor to openList
            else if tentative_g >= neighbor.g:
                continue  // This path is not better
                
            // This path is the best so far
            neighbor.parent = current
            neighbor.g = tentative_g
            neighbor.h = heuristic(neighbor, goal)
            neighbor.f = neighbor.g + neighbor.h
    
    return failure  // No path exists
function reconstruct_path(current):
    path = []
    while current is not null:
        add current to beginning of path
        current = current.parent
    return path

Let's break down each component of this implementation:

Initialization phase

The algorithm begins by setting up two essential lists:

• The open list starts with just the starting node
• The closed list begins empty

Each node stores four critical pieces of information:

• g: The actual cost from the start node
• h: The estimated cost to the goal
• f: The sum of g and h
• parent: Reference to the previous node (for path reconstruction)

Main loop

The core of A* is its main loop, which continues until either:

• The goal is reached (success)
• The open list becomes empty (failure - no path exists)

During each iteration, the algorithm:

1. Selects the most promising node (lowest f value) from the open list
2. Moves it to the closed list
3. Examines all neighboring nodes

Neighbor evaluation

For each neighbor, the algorithm:

• Skips nodes already in the closed list
• Calculates a tentative g score
• Updates node values if a better path is found
• Adds new nodes to the open list

Path reconstruction

Once the goal is reached, the algorithm works backward through the parent references to construct the optimal path from start to goal.

This systematic approach ensures that A* will always find the optimal path if:

1. The heuristic function is admissible (never overestimates)
2. A path actually exists between the start and goal nodes

In the next section, we'll translate this pseudocode into a practical Python implementation, complete with visualizations to help you understand how the algorithm explores the search space.

Python Implementation of A* Algorithm

Now that we understand the theory and pseudocode, let's implement A* in Python. We'll create a practical implementation that you can use as a foundation for your own projects. To make this concrete, we'll implement the algorithm on a 2D grid—a common scenario in games and robotics applications.

Step 1: Essential functions and imports

We first import necessary libraries and create a node structure that will store position and pathfinding information for each point in our search space.

from typing import List, Tuple, Dict, Set
import numpy as np
import heapq
from math import sqrt
def create_node(position: Tuple[int, int], g: float = float('inf'), 
                h: float = 0.0, parent: Dict = None) -> Dict:
    """
    Create a node for the A* algorithm.
    
    Args:
        position: (x, y) coordinates of the node
        g: Cost from start to this node (default: infinity)
        h: Estimated cost from this node to goal (default: 0)
        parent: Parent node (default: None)
    
    Returns:
        Dictionary containing node information
    """
    return {
        'position': position,
        'g': g,
        'h': h,
        'f': g + h,
        'parent': parent
    }

Step 2: Helper functions

To support our pathfinding algorithm, we'll create several helper functions. First, we'll implement a function to calculate distances between points using Euclidean distance.

Then, we'll add a function to find valid neighboring positions in our grid, carefully checking boundaries and obstacles. Finally, we'll create a function that helps us reconstruct the path once we've found our goal.

def calculate_heuristic(pos1: Tuple[int, int], pos2: Tuple[int, int]) -> float:
    """
    Calculate the estimated distance between two points using Euclidean distance.
    """
    x1, y1 = pos1
    x2, y2 = pos2
    return sqrt((x2 - x1)**2 + (y2 - y1)**2)
def get_valid_neighbors(grid: np.ndarray, position: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Get all valid neighboring positions in the grid.
    
    Args:
        grid: 2D numpy array where 0 represents walkable cells and 1 represents obstacles
        position: Current position (x, y)
    
    Returns:
        List of valid neighboring positions
    """
    x, y = position
    rows, cols = grid.shape
    
    # All possible moves (including diagonals)
    possible_moves = [
        (x+1, y), (x-1, y),    # Right, Left
        (x, y+1), (x, y-1),    # Up, Down
        (x+1, y+1), (x-1, y-1),  # Diagonal moves
        (x+1, y-1), (x-1, y+1)
    ]
    
    return [
        (nx, ny) for nx, ny in possible_moves
        if 0 <= nx < rows and 0 <= ny < cols  # Within grid bounds
        and grid[nx, ny] == 0                # Not an obstacle
    ]
def reconstruct_path(goal_node: Dict) -> List[Tuple[int, int]]:
    """
    Reconstruct the path from goal to start by following parent pointers.
    """
    path = []
    current = goal_node
    
    while current is not None:
        path.append(current['position'])
        current = current['parent']
        
    return path[::-1]  # Reverse to get path from start to goal

Step 3: Main A* algorithm implementation

Now let’s implement our algorithm. We'll use a priority queue to make sure we always explore the most promising paths first. 

Our algorithm will maintain two sets: an open set for nodes we still need to explore and a closed set for nodes we've already checked. 

As we explore the grid, we'll continuously update path costs whenever we find better routes until we reach our goal.

def find_path(grid: np.ndarray, start: Tuple[int, int], 
              goal: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Find the optimal path using A* algorithm.
    
    Args:
        grid: 2D numpy array (0 = free space, 1 = obstacle)
        start: Starting position (x, y)
        goal: Goal position (x, y)
    
    Returns:
        List of positions representing the optimal path
    """
    # Initialize start node
    start_node = create_node(
        position=start,
        g=0,
        h=calculate_heuristic(start, goal)
    )
    
    # Initialize open and closed sets
    open_list = [(start_node['f'], start)]  # Priority queue
    open_dict = {start: start_node}         # For quick node lookup
    closed_set = set()                      # Explored nodes
    
    while open_list:
        # Get node with lowest f value
        _, current_pos = heapq.heappop(open_list)
        current_node = open_dict[current_pos]
        
        # Check if we've reached the goal
        if current_pos == goal:
            return reconstruct_path(current_node)
            
        closed_set.add(current_pos)
        
        # Explore neighbors
        for neighbor_pos in get_valid_neighbors(grid, current_pos):
            # Skip if already explored
            if neighbor_pos in closed_set:
                continue
                
            # Calculate new path cost
            tentative_g = current_node['g'] + calculate_heuristic(current_pos, neighbor_pos)
            
            # Create or update neighbor
            if neighbor_pos not in open_dict:
                neighbor = create_node(
                    position=neighbor_pos,
                    g=tentative_g,
                    h=calculate_heuristic(neighbor_pos, goal),
                    parent=current_node
                )
                heapq.heappush(open_list, (neighbor['f'], neighbor_pos))
                open_dict[neighbor_pos] = neighbor
            elif tentative_g < open_dict[neighbor_pos]['g']:
                # Found a better path to the neighbor
                neighbor = open_dict[neighbor_pos]
                neighbor['g'] = tentative_g
                neighbor['f'] = tentative_g + neighbor['h']
                neighbor['parent'] = current_node
    
    return []  # No path found

Step 4: Visualization

Now, let’s create a visualization function. This will show us our grid layout with any obstacles, draw our calculated optimal path, and clearly mark our start and goal positions.

import matplotlib.pyplot as plt
def visualize_path(grid: np.ndarray, path: List[Tuple[int, int]]):
    """
    Visualize the grid and found path.
    """
    plt.figure(figsize=(10, 10))
    plt.imshow(grid, cmap='binary')
    
    if path:
        path = np.array(path)
        plt.plot(path[:, 1], path[:, 0], 'b-', linewidth=3, label='Path')
        plt.plot(path[0, 1], path[0, 0], 'go', markersize=15, label='Start')
        plt.plot(path[-1, 1], path[-1, 0], 'ro', markersize=15, label='Goal')
    
    plt.grid(True)
    plt.legend(fontsize=12)
    plt.title("A* Pathfinding Result")
    plt.show()

Example usage

Here's how to use the implementation:

# Create a sample grid
grid = np.zeros((20, 20))  # 20x20 grid, all free space initially
# Add some obstacles
grid[5:15, 10] = 1  # Vertical wall
grid[5, 5:15] = 1   # Horizontal wall
# Define start and goal positions
start_pos = (2, 2)
goal_pos = (18, 18)
# Find the path
path = find_path(grid, start_pos, goal_pos)
if path:
    print(f"Path found with {len(path)} steps!")
    visualize_path(grid, path)
else:
    print("No path found!")

Output

Path found with 22 steps!

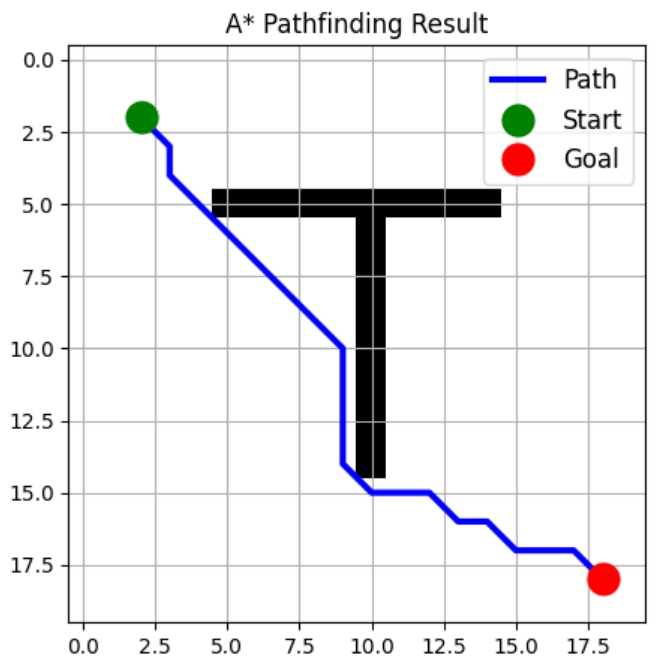
This implementation is both efficient and extensible. You can easily modify it to:

• Use different heuristic functions
• Support different types of movement
• Handle weighted grids
• Include additional constraints

In the next section, we'll look at some practical applications of this algorithm and see how it's used in real-world scenarios.

Applications of A* Search Algorithm

The A* algorithm's efficiency and flexibility make it valuable across numerous domains. Here are the key areas where it excels:

1. Video Games and entertainment

The A* search algorithm is extensively used in video game development due to its optimal pathfinding capabilities. It enhances the player experience by allowing for more realistic and responsive character movement.

• Character pathfinding in strategy games: A* helps characters find the shortest or safest path to a target, crucial in real-time strategy (RTS) games where units need to navigate around obstacles and enemies effectively.
• NPC movement in open-world environments: Non-playable characters (NPCs) use A* to navigate large and dynamic game worlds, allowing them to reach objectives while avoiding obstacles and other characters.
• Real-time tactical planning in combat scenarios: A* is used to calculate the efficient movement and positioning of units during combat, ensuring that characters can quickly reach advantageous spots while avoiding danger.
• Maze solving in puzzle games: A* is an effective algorithm for navigating complex mazes, giving players an engaging challenge by powering dynamic maze-solving opponents or providing hints.

2. Navigation systems

A* is widely used in navigation systems to optimize routes, accounting for various factors like distance and potential obstacles.

• Route planning in GPS applications: A* finds the shortest and fastest route between two points, making it an essential component of GPS software used by millions worldwide.
• Traffic-aware navigation services: In modern navigation apps, A* is combined with real-time traffic data to suggest the best route, minimizing travel time and avoiding congested roads.
• Public transport route optimization: A* can help find optimal routes that incorporate multiple modes of public transport, ensuring users make efficient transfers.
• Indoor navigation systems: A* is also used in indoor navigation, such as in airports or large shopping malls, where it helps guide users through complex environments with multiple levels and obstacles.

3. Robotics and automation

The A* algorithm is crucial for robotics, where efficient movement is essential for productivity and safety.

• Autonomous vehicle path planning: Self-driving cars use A* to navigate roads, making decisions in real time about how to move from point A to point B while avoiding collisions and adhering to traffic rules.
• Warehouse robot navigation: In automated warehouses, robots rely on A* to navigate efficiently between storage racks to pick and place items, minimizing delays and avoiding collisions with other robots.
• Drone flight path optimization: A* helps drones plan efficient flight paths, whether for delivery, surveying, or recreational use, ensuring they avoid obstacles and follow optimal routes.
• Manufacturing robot movement planning: In factory settings, A* is used to ensure robots can move seamlessly between workstations, avoiding collisions with other machinery and maintaining productivity.

4. Network systems

A* is also applied in optimizing network operations, where efficiency in resource utilization and routing is paramount.

• Network packet routing: A* is used to determine the most efficient path for data packets to travel across a network, ensuring minimal latency and high reliability.
• Resource allocation in distributed systems: A* aids in optimizing resource allocation, enabling distributed systems to efficiently allocate tasks across various nodes while minimizing overhead.
• Circuit board path design: When designing printed circuit boards (PCBs), A* can be used to determine optimal paths for electrical traces, ensuring minimal interference and efficient layout.
• Network cable routing optimization: A* is employed in designing physical network infrastructures, finding the most effective routes for cables to minimize cost and maximize performance.

What makes A* particularly valuable is its adaptability through custom heuristic functions, allowing optimization for different metrics like distance, time, or energy usage.

In the next section, we’ll look at some common challenges and optimization techniques for implementing A* effectively.

Common Challenges and Optimization Techniques

While A* is powerful, implementing it effectively requires addressing several common challenges. The most significant hurdle developers face is managing resources efficiently, particularly when dealing with large search spaces.

The primary challenges include:

• Memory consumption in large graphs
• Performance bottlenecks with complex heuristics
• Handling tie-breaking situations
• Balancing accuracy vs. computation speed

Fortunately, there are several effective optimization strategies to address these challenges:

• For memory management, focus on efficient data structures
• Use binary heaps for the open list instead of arrays
• Implement a hash table for faster closed list lookups
• Clear unnecessary node data after processing

When performance is critical, consider these speed improvements:

• Simplify heuristic calculations where possible
• Use integer arithmetic instead of floating-point
• Implement hierarchical pathfinding for large maps

One particularly effective approach for large spaces is bilateral search—searching from both the start and goal simultaneously. Additionally, when working with grid-based pathfinding, you can significantly improve performance by pre-computing heuristic values or using lookup tables.

Remember to choose optimization techniques based on your specific requirements and constraints. The key is finding the right balance between memory usage and computational speed for your application.

Conclusion

The A* algorithm stands as a fundamental tool in pathfinding and graph traversal problems. Through this guide, we have seen its core concepts, implemented a practical solution in Python, and examined its diverse applications. The algorithm's strength lies in its balance of accuracy and efficiency, making it invaluable across various domains from gaming to robotics.

While implementing A* comes with its challenges, the optimization techniques we've discussed can help you create efficient solutions. If you're developing games, planning robot paths, or solving routing problems, then understanding the A* algorithm provides you with a powerful approach to finding optimal paths in your applications

Building such sophisticated algorithms requires a solid foundation in Python programming concepts and best practices. Want to strengthen your Python foundations and tackle more advanced algorithms like A*? 

Take your programming skills to the next level with our Intermediate Python for Developers Course course, where you'll master custom functions, explore essential modules, and build sophisticated applications.