Der A*-Algorithmus: Ein vollständiger Leitfaden

Algorithmen zur Durchquerung von Graphen sind grundlegend für viele Anwendungen in der Informatik, von der Spieleentwicklung bis zur Robotik. Diese Algorithmen wurden entwickelt, um Graphen zu erforschen und durch sie zu navigieren. Graphen sind Datenstrukturen, die aus Knoten (Vertices) und Kanten bestehen. Unter diesen Algorithmen sticht der A*-Algorithmus als besonders effizienter und vielseitiger Ansatz zum Finden optimaler Pfade hervor.

Der A*-Algorithmus ist ein informierter Suchalgorithmus, das heißt, er nutzt eine heuristische Funktion, um seine Suche auf das Ziel auszurichten. Diese heuristische Funktion schätzt die Kosten für das Erreichen des Ziels von einem bestimmten Knotenpunkt aus und ermöglicht es dem Algorithmus, vielversprechende Pfade zu priorisieren und unnötige Pfade zu vermeiden.

In diesem Artikel werden wir uns die wichtigsten Konzepte des A*-Algorithmus, seine Implementierung in Python, seine Anwendungen sowie seine Vorteile und Grenzen ansehen.

Wenn du mehr über die Programmierung mit Python erfahren möchtest, schau dir unseren Kurs Einführung in Python für Entwickler Kurs.

Was ist der A*-Algorithmus?

Der A*-Algorithmus ist ein leistungsstarker und weit verbreiteter Algorithmus zur Durchquerung von Graphen und zur Pfadfindung. Es findet den kürzesten Weg zwischen einem Startknoten und einem Zielknoten in einem gewichteten Graphen. 

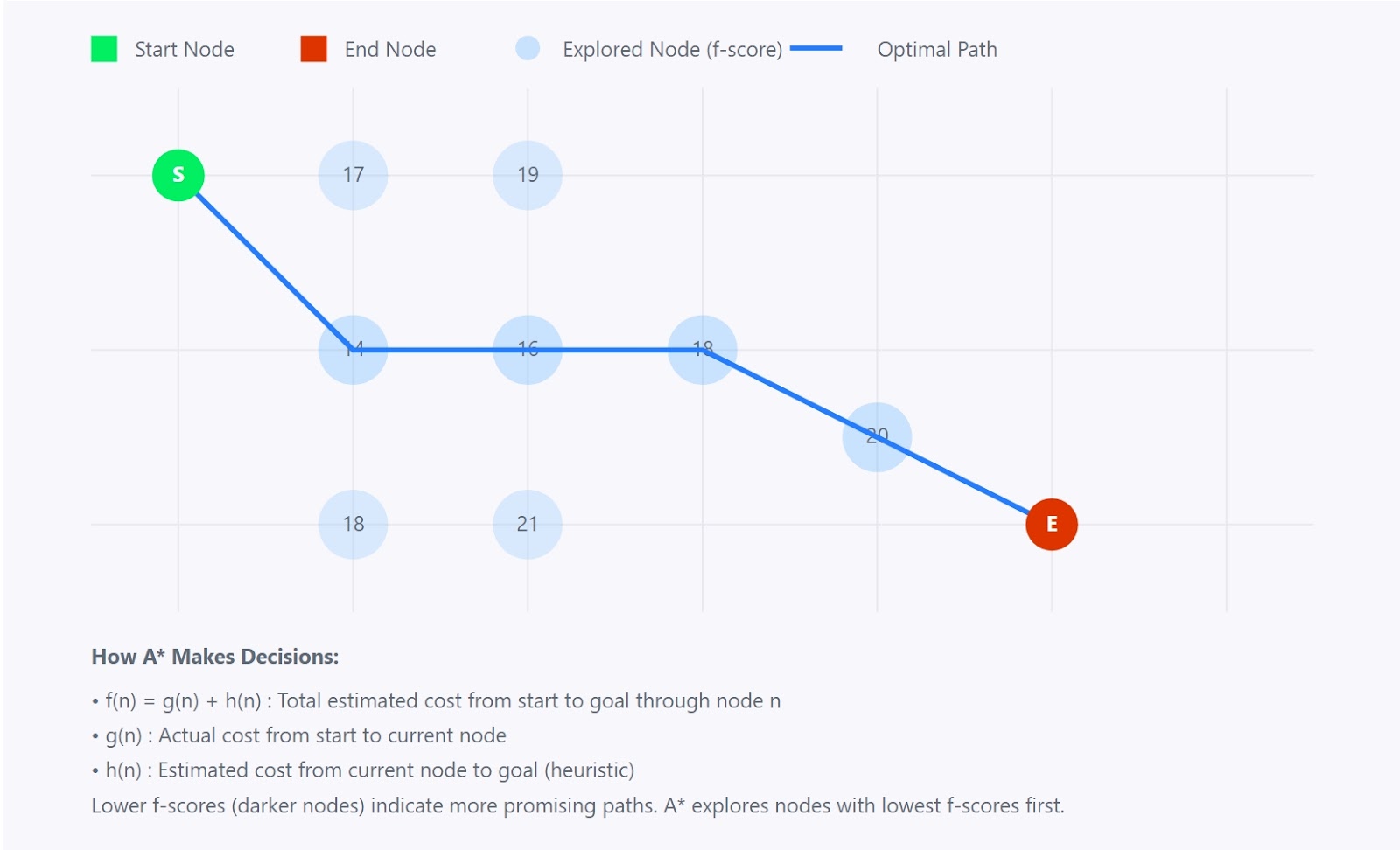
A*-Algorithmus

Wie funktioniert der A*-Algorithmus?

Der A*-Algorithmus kombiniert die besten Aspekte von zwei anderen Algorithmen:

1. Dijkstra's Algorithmus: Dieser Algorithmus findet den kürzesten Weg zu allen Knotenpunkten von einem einzigen Ausgangsknotenpunkt aus.
2. Gierige Best-First-Suche: Dieser Algorithmus erkundet den Knotenpunkt, der dem Ziel am nächsten zu sein scheint, basierend auf einer heuristischen Funktion.

Stell dir vor, du versuchst, die kürzeste Route zwischen zwei Städten auf einer Karte zu finden. Während Dijkstras Algorithmus in alle Richtungen suchen würde und Best-First Search direkt auf das Ziel zusteuert (und dabei möglicherweise Abkürzungen verpasst), macht A* etwas Schlaueres. Sie berücksichtigt beides:

• Die bereits zurückgelegte Strecke vom Start
• Eine intelligente Schätzung der verbleibenden Entfernung zum Ziel

Diese Kombination hilft A*, fundierte Entscheidungen darüber zu treffen, welcher Weg als Nächstes erkundet werden soll, und macht es so effizient und genau.

Schlüsselkomponenten

Um den A*-Algorithmus zu verstehen, musst du mit diesen grundlegenden Konzepten vertraut sein:

• Knotenpunkte: Punkte in deinem Diagramm (wie Schnittpunkte auf einer Karte)
• Ränder: Verbindungen zwischen Knotenpunkten (wie Straßen, die Kreuzungen verbinden)
• Pfadkosten: Die tatsächlichen Kosten für den Wechsel von einem Knotenpunkt zu einem anderen
• Heuristic: Geschätzte Kosten von einem beliebigen Knotenpunkt zum Ziel
• Suche Raum: Die Sammlung aller möglichen Pfade zum Erkunden

Im nächsten Abschnitt werden wir uns diese Konzepte genauer ansehen und sehen, wie A* sie nutzt, um optimale Wege zu finden.

Schlüsselbegriffe der A*-Suche

Die Effizienz des A*-Algorithmus beruht auf der intelligenten Auswertung der Pfade anhand der drei Schlüsselkomponenten g(n), h(n) und f(n). Diese Komponenten wirken zusammen, um den Suchprozess auf die vielversprechendsten Wege zu lenken.

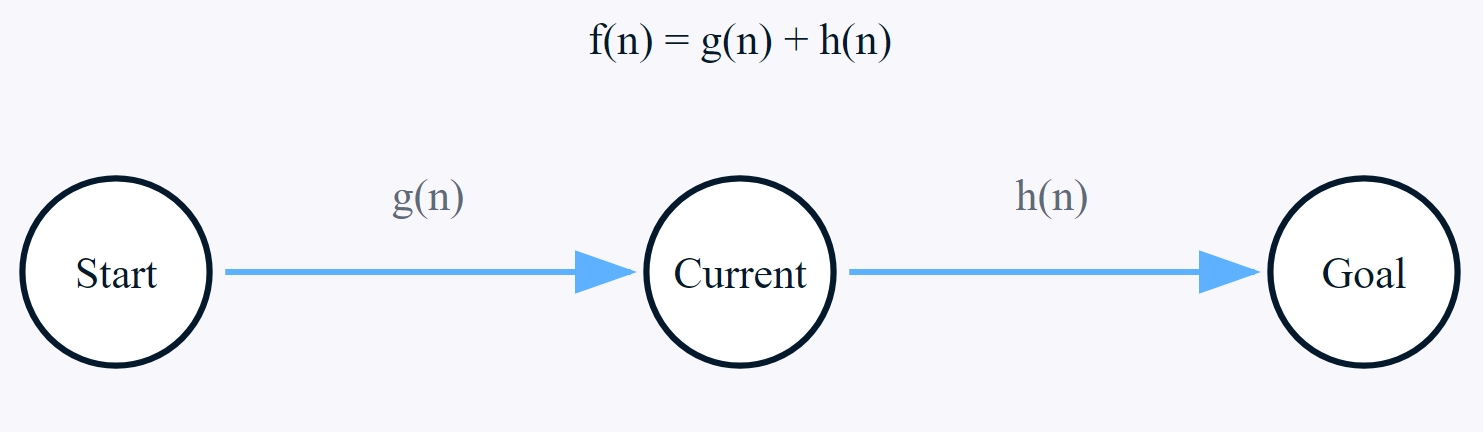
A*-Algorithmus Kostenfunktion

Verstehen der Kostenfunktionen

Pfadkosten g(n)

Die Pfadkostenfunktion g(n) stellt die genaue, bekannte Entfernung vom anfänglichen Startknoten zur aktuellen Position in unserer Suche dar. Im Gegensatz zu den geschätzten Werten sind diese Kosten genau und werden durch die Addition aller einzelnen Kantengewichte berechnet, die entlang des gewählten Pfades durchlaufen wurden. 

Mathematisch gesehen kann ein Pfad durch die Knoten n0(Startknoten) bis nk​ (aktueller Knoten), können wir g(n) ausdrücken als:

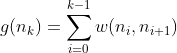
Wo:

• w(n_i,n_i+1) steht für das Gewicht der Kante, die den Knoten ni mit dem Knoten n_i+1​.

Während wir uns durch das Diagramm bewegen, sammelt sich dieser Wert an und gibt uns ein klares Maß für die tatsächlichen Ressourcen (sei es die Entfernung, die Zeit oder eine andere Kennzahl), die wir aufgewendet haben, um unsere aktuelle Position zu erreichen.

Heuristische Funktion h(n)

Die heuristische Funktion h(n) gibt die geschätzten Kosten vom aktuellen Knotenpunkt zum Zielknotenpunkt an und dient dem Algorithmus als "informierte Vermutung" über den verbleibenden Weg. 

Mathematisch gesehen muss die heuristische Schätzung für jeden gegebenen Knoten n die Bedingung erfüllen h(n)≤h*(n) erfüllen, wobei h*(n) die tatsächlichen Kosten für das Ziel sind, so dass es zulässig ist, die wahren Kosten nicht zu überschätzen.

Bei gitterbasierten oder kartenähnlichen Problemen sind gängige heuristische Funktionen die Manhattan-Abstand und Euklidischer Abstand. Für die Koordinaten (x₁,y₁) des aktuellen Knotens und (x₂,y₂) des Zielknotens, werden diese Entfernungen wie folgt berechnet:

Manhattan Entfernung

Euklidischer Abstand

Geschätzte Gesamtkosten f(n)

Die geschätzten Gesamtkosten f(n) sind der Eckpfeiler des Entscheidungsprozesses des A*-Algorithmus, der sowohl die tatsächlichen Pfadkosten als auch die heuristische Schätzung kombiniert, um das Potenzial eines jeden Knotens zu bewerten. Für jeden Knoten n werden diese Kosten wie folgt berechnet:

Wo:

• g(n) steht für die tatsächlichen Kosten vom Startpunkt bis zum aktuellen Knotenpunkt,
• h(n) steht für die geschätzten Kosten vom aktuellen Knotenpunkt zum Ziel.

Der Algorithmus verwendet diesen kombinierten Wert, um strategisch zu entscheiden, welcher Knoten als Nächstes erkundet werden soll, wobei er immer den Knoten mit dem niedrigsten f(n) Wert aus der offenen Liste und sorgt so für ein optimales Gleichgewicht zwischen den bekannten Kosten und den geschätzten verbleibenden Entfernungen.

Knotenlisten verwalten

Der A*-Algorithmus unterhält zwei wesentliche Listen

Offene Liste:

• Enthält Knotenpunkte, die ausgewertet werden müssen
• Sortiert nach f(n)-Wert (niedrigster Wert zuerst)
• Neue Knotenpunkte werden hinzugefügt, sobald sie entdeckt werden

Geschlossene Liste:

• Enthält bereits ausgewertete Knoten
• Hilft, die Neubewertung von Knoten zu vermeiden
• Wird verwendet, um den endgültigen Pfad zu rekonstruieren

Der Algorithmus wählt kontinuierlich den Knoten mit dem niedrigsten f(n) Wert aus der offenen Liste, wertet ihn aus und verschiebt ihn in die geschlossene Liste, bis er den Zielknoten erreicht oder feststellt, dass kein Pfad existiert.

A* Suchalgorithmus Pseudocode

Nachdem wir nun die grundlegenden Komponenten von A* verstanden haben, wollen wir sehen, wie sie in der Praxis zusammenkommen. Die Umsetzung des Algorithmus kann in klare, logische Schritte zerlegt werden, die diese Konzepte in eine funktionierende Lösung zur Wegfindung umwandeln.

Hier siehst du, wie der Algorithmus Schritt für Schritt funktioniert:

function A_Star(start, goal):
    // Initialize open and closed lists
    openList = [start]          // Nodes to be evaluated
    closedList = []            // Nodes already evaluated
    
    // Initialize node properties
    start.g = 0                // Cost from start to start is 0
    start.h = heuristic(start, goal)  // Estimate to goal
    start.f = start.g + start.h       // Total estimated cost
    start.parent = null              // For path reconstruction
    while openList is not empty:
        // Get node with lowest f value - implement using a priority queue
       // for faster retrieval of the best node
        current = node in openList with lowest f value
        
        // Check if we've reached the goal
        if current = goal:
            return reconstruct_path(current)
            
        // Move current node from open to closed list
        remove current from openList
        add current to closedList
        
        // Check all neighboring nodes
        for each neighbor of current:
            if neighbor in closedList:
                continue  // Skip already evaluated nodes
                
            // Calculate tentative g score
            tentative_g = current.g + distance(current, neighbor)
            
            if neighbor not in openList:
                add neighbor to openList
            else if tentative_g >= neighbor.g:
                continue  // This path is not better
                
            // This path is the best so far
            neighbor.parent = current
            neighbor.g = tentative_g
            neighbor.h = heuristic(neighbor, goal)
            neighbor.f = neighbor.g + neighbor.h
    
    return failure  // No path exists
function reconstruct_path(current):
    path = []
    while current is not null:
        add current to beginning of path
        current = current.parent
    return path

Schauen wir uns die einzelnen Komponenten dieser Umsetzung an:

Initialisierungsphase

Der Algorithmus beginnt mit der Erstellung von zwei wichtigen Listen:

• Die offene Liste beginnt nur mit dem Startknoten
• Die geschlossene Liste beginnt leer

Jeder Knotenpunkt speichert vier wichtige Informationen:

• g: Die tatsächlichen Kosten ab dem Startknoten
• h: Die geschätzten Kosten für das Ziel
• f: Die Summe aus g und h
• Elternteil: Verweis auf den vorherigen Knoten (für die Pfadrekonstruktion)

Hauptschleife

Der Kern von A* ist die Hauptschleife, die so lange läuft, bis entweder:

• Das Ziel ist erreicht (Erfolg)
• Die offene Liste wird leer (Fehler - kein Pfad vorhanden)

Während jeder Iteration wird der Algorithmus:

1. Wählt den vielversprechendsten Knoten (niedrigster f-Wert) aus der offenen Liste aus
2. Verschiebt es in die geschlossene Liste
3. Untersucht alle benachbarten Knotenpunkte

Bewertung durch den Nachbarn

Für jeden Nachbarn wird der Algorithmus:

• Überspringt Knoten, die sich bereits in der geschlossenen Liste befinden
• Berechnet einen vorläufigen g-Wert
• Aktualisiert Knotenwerte, wenn ein besserer Pfad gefunden wird
• Fügt der Liste der offenen Knoten neue Knoten hinzu

Pfadrekonstruktion

Sobald das Ziel erreicht ist, arbeitet sich der Algorithmus rückwärts durch die übergeordneten Referenzen, um den optimalen Pfad vom Start zum Ziel zu konstruieren.

Dieser systematische Ansatz stellt sicher, dass A* immer den optimalen Weg findet, wenn:

1. Die heuristische Funktion ist zulässig (überschätzt nie)
2. Zwischen dem Start- und dem Zielknoten existiert tatsächlich ein Pfad

Im nächsten Abschnitt übersetzen wir diesen Pseudocode in eine praktische Python-Implementierung mit Visualisierungen, die dir zeigen, wie der Algorithmus den Suchraum erkundet.

Python Implementierung des A* Algorithmus

Nachdem wir nun die Theorie und den Pseudocode verstanden haben, wollen wir A* in Python implementieren. Wir erstellen eine praktische Umsetzung, die du als Grundlage für deine eigenen Projekte nutzen kannst. Um dies zu verdeutlichen, werden wir den Algorithmus auf einem 2D-Gitter implementieren - ein übliches Szenario in Spielen und Robotik-Anwendungen.

Schritt 1: Wesentliche Funktionen und Importe

Zuerst importieren wir die notwendigen Bibliotheken und erstellen eine Knotenstruktur, in der wir die Positions- und Pfadfindungsinformationen für jeden Punkt in unserem Suchraum speichern.

from typing import List, Tuple, Dict, Set
import numpy as np
import heapq
from math import sqrt
def create_node(position: Tuple[int, int], g: float = float('inf'), 
                h: float = 0.0, parent: Dict = None) -> Dict:
    """
    Create a node for the A* algorithm.
    
    Args:
        position: (x, y) coordinates of the node
        g: Cost from start to this node (default: infinity)
        h: Estimated cost from this node to goal (default: 0)
        parent: Parent node (default: None)
    
    Returns:
        Dictionary containing node information
    """
    return {
        'position': position,
        'g': g,
        'h': h,
        'f': g + h,
        'parent': parent
    }

Schritt 2: Hilfsfunktionen

Um unseren Pfadfindungsalgorithmus zu unterstützen, werden wir mehrere Hilfsfunktionen erstellen. Zuerst werden wir eine Funktion implementieren, die Abstände zwischen Punkten mithilfe des euklidischen Abstands berechnet.

Dann fügen wir eine Funktion hinzu, die gültige Nachbarpositionen in unserem Raster findet und dabei Grenzen und Hindernisse sorgfältig prüft. Zum Schluss erstellen wir eine Funktion, die uns hilft, den Weg zu rekonstruieren, wenn wir unser Ziel gefunden haben.

def calculate_heuristic(pos1: Tuple[int, int], pos2: Tuple[int, int]) -> float:
    """
    Calculate the estimated distance between two points using Euclidean distance.
    """
    x1, y1 = pos1
    x2, y2 = pos2
    return sqrt((x2 - x1)**2 + (y2 - y1)**2)
def get_valid_neighbors(grid: np.ndarray, position: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Get all valid neighboring positions in the grid.
    
    Args:
        grid: 2D numpy array where 0 represents walkable cells and 1 represents obstacles
        position: Current position (x, y)
    
    Returns:
        List of valid neighboring positions
    """
    x, y = position
    rows, cols = grid.shape
    
    # All possible moves (including diagonals)
    possible_moves = [
        (x+1, y), (x-1, y),    # Right, Left
        (x, y+1), (x, y-1),    # Up, Down
        (x+1, y+1), (x-1, y-1),  # Diagonal moves
        (x+1, y-1), (x-1, y+1)
    ]
    
    return [
        (nx, ny) for nx, ny in possible_moves
        if 0 <= nx < rows and 0 <= ny < cols  # Within grid bounds
        and grid[nx, ny] == 0                # Not an obstacle
    ]
def reconstruct_path(goal_node: Dict) -> List[Tuple[int, int]]:
    """
    Reconstruct the path from goal to start by following parent pointers.
    """
    path = []
    current = goal_node
    
    while current is not None:
        path.append(current['position'])
        current = current['parent']
        
    return path[::-1]  # Reverse to get path from start to goal

Schritt 3: Hauptimplementierung des A*-Algorithmus

Nun wollen wir unseren Algorithmus implementieren. Wir verwenden eine Prioritäts-Warteschlange, um sicherzustellen, dass wir immer die vielversprechendsten Wege zuerst erkunden. 

Unser Algorithmus behält zwei Mengen bei: eine offene Menge für Knoten, die wir noch untersuchen müssen, und eine geschlossene Menge für Knoten, die wir bereits überprüft haben. 

Während wir das Netz erkunden, aktualisieren wir die Pfadkosten kontinuierlich, wenn wir bessere Routen finden, bis wir unser Ziel erreichen.

def find_path(grid: np.ndarray, start: Tuple[int, int], 
              goal: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Find the optimal path using A* algorithm.
    
    Args:
        grid: 2D numpy array (0 = free space, 1 = obstacle)
        start: Starting position (x, y)
        goal: Goal position (x, y)
    
    Returns:
        List of positions representing the optimal path
    """
    # Initialize start node
    start_node = create_node(
        position=start,
        g=0,
        h=calculate_heuristic(start, goal)
    )
    
    # Initialize open and closed sets
    open_list = [(start_node['f'], start)]  # Priority queue
    open_dict = {start: start_node}         # For quick node lookup
    closed_set = set()                      # Explored nodes
    
    while open_list:
        # Get node with lowest f value
        _, current_pos = heapq.heappop(open_list)
        current_node = open_dict[current_pos]
        
        # Check if we've reached the goal
        if current_pos == goal:
            return reconstruct_path(current_node)
            
        closed_set.add(current_pos)
        
        # Explore neighbors
        for neighbor_pos in get_valid_neighbors(grid, current_pos):
            # Skip if already explored
            if neighbor_pos in closed_set:
                continue
                
            # Calculate new path cost
            tentative_g = current_node['g'] + calculate_heuristic(current_pos, neighbor_pos)
            
            # Create or update neighbor
            if neighbor_pos not in open_dict:
                neighbor = create_node(
                    position=neighbor_pos,
                    g=tentative_g,
                    h=calculate_heuristic(neighbor_pos, goal),
                    parent=current_node
                )
                heapq.heappush(open_list, (neighbor['f'], neighbor_pos))
                open_dict[neighbor_pos] = neighbor
            elif tentative_g < open_dict[neighbor_pos]['g']:
                # Found a better path to the neighbor
                neighbor = open_dict[neighbor_pos]
                neighbor['g'] = tentative_g
                neighbor['f'] = tentative_g + neighbor['h']
                neighbor['parent'] = current_node
    
    return []  # No path found

Schritt 4: Visualisierung

Jetzt wollen wir eine Visualisierungsfunktion erstellen. Das zeigt uns unser Raster mit allen Hindernissen, zeichnet unseren berechneten optimalen Pfad und markiert deutlich unsere Start- und Zielposition.

import matplotlib.pyplot as plt
def visualize_path(grid: np.ndarray, path: List[Tuple[int, int]]):
    """
    Visualize the grid and found path.
    """
    plt.figure(figsize=(10, 10))
    plt.imshow(grid, cmap='binary')
    
    if path:
        path = np.array(path)
        plt.plot(path[:, 1], path[:, 0], 'b-', linewidth=3, label='Path')
        plt.plot(path[0, 1], path[0, 0], 'go', markersize=15, label='Start')
        plt.plot(path[-1, 1], path[-1, 0], 'ro', markersize=15, label='Goal')
    
    plt.grid(True)
    plt.legend(fontsize=12)
    plt.title("A* Pathfinding Result")
    plt.show()

Beispiel Verwendung

Hier erfährst du, wie du die Implementierung nutzen kannst:

# Create a sample grid
grid = np.zeros((20, 20))  # 20x20 grid, all free space initially
# Add some obstacles
grid[5:15, 10] = 1  # Vertical wall
grid[5, 5:15] = 1   # Horizontal wall
# Define start and goal positions
start_pos = (2, 2)
goal_pos = (18, 18)
# Find the path
path = find_path(grid, start_pos, goal_pos)
if path:
    print(f"Path found with {len(path)} steps!")
    visualize_path(grid, path)
else:
    print("No path found!")

Ausgabe

Pfad mit 22 Schritten gefunden!

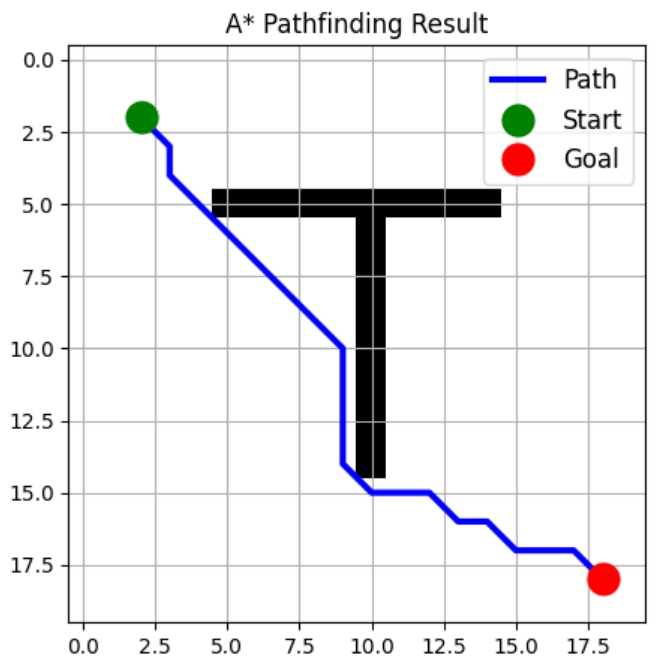
Diese Implementierung ist sowohl effizient als auch erweiterbar. Du kannst es ganz einfach ändern:

• Verschiedene heuristische Funktionen verwenden
• Unterstützt verschiedene Arten von Bewegungen
• Gewogene Gitter handhaben
• Zusätzliche Beschränkungen einbeziehen

Im nächsten Abschnitt werden wir uns einige praktische Anwendungen dieses Algorithmus ansehen und sehen, wie er in der Praxis eingesetzt wird.

Anwendungen des A*-Suchalgorithmus

Die Effizienz und Flexibilität des A*-Algorithmus machen ihn in vielen Bereichen wertvoll. Hier sind die wichtigsten Bereiche, in denen es sich auszeichnet:

1. Videospiele und Unterhaltung

Der A*-Suchalgorithmus wird in der Entwicklung von Videospielen häufig eingesetzt, da er eine optimale Wegfindung ermöglicht. Sie verbessert das Spielerlebnis, indem sie realistischere und reaktionsschnellere Charakterbewegungen ermöglicht.

• Die Wegfindung von Charakteren in Strategiespielen: A* hilft den Charakteren, den kürzesten oder sichersten Weg zu einem Ziel zu finden, was in Echtzeitstrategiespielen (RTS), in denen die Einheiten Hindernisse und Feinde effektiv umfahren müssen, von entscheidender Bedeutung ist.
• NPC-Bewegung in Open-World-Umgebungen: Nicht-spielbare Charaktere (NPCs) nutzen A*, um in großen und dynamischen Spielwelten zu navigieren. So können sie Ziele erreichen und gleichzeitig Hindernissen und anderen Charakteren ausweichen.
• Taktische Planung in Echtzeit in Kampfszenarien: A* wird verwendet, um die effiziente Bewegung und Positionierung von Einheiten während des Kampfes zu berechnen und sicherzustellen, dass die Charaktere schnell vorteilhafte Stellen erreichen und gleichzeitig Gefahren vermeiden können.
• Das Lösen von Labyrinthen in Puzzlespielen: A* ist ein effektiver Algorithmus zum Navigieren in komplexen Labyrinthen, der die Spieler/innen vor eine spannende Herausforderung stellt, indem er dynamische Labyrinth-Lösungs-Gegner antreibt oder Hinweise gibt.

2. Navigationssysteme

A* wird häufig in Navigationssystemen verwendet, um Routen zu optimieren und dabei verschiedene Faktoren wie Entfernungen und mögliche Hindernisse zu berücksichtigen.

• Routenplanung in GPS-Anwendungen: A* findet die kürzeste und schnellste Route zwischen zwei Punkten und ist damit ein wesentlicher Bestandteil der GPS-Software, die von Millionen Menschen weltweit genutzt wird.
• Verkehrsabhängige Navigationsdienste: In modernen Navigations-Apps wird A* mit Echtzeit-Verkehrsdaten kombiniert, um die beste Route vorzuschlagen, die Reisezeit zu minimieren und verstopfte Straßen zu vermeiden.
• Routenoptimierung im öffentlichen Verkehr: A* kann dabei helfen, optimale Routen zu finden, die mehrere öffentliche Verkehrsmittel einbeziehen, damit die Nutzer effizient umsteigen können.
• Indoor-Navigationssysteme: A* wird auch bei der Navigation in Innenräumen eingesetzt, z. B. auf Flughäfen oder in großen Einkaufszentren, wo es dabei hilft, die Nutzer durch komplexe Umgebungen mit mehreren Ebenen und Hindernissen zu führen.

3. Robotik und Automatisierung

Der A*-Algorithmus ist entscheidend für die Robotik, in der effiziente Bewegungen für Produktivität und Sicherheit unerlässlich sind.

• Autonome Fahrzeugwegplanung: Selbstfahrende Autos nutzen A*, um auf den Straßen zu navigieren. Sie treffen in Echtzeit Entscheidungen darüber, wie sie von A nach B kommen und dabei Kollisionen vermeiden und sich an die Verkehrsregeln halten.
• Lagerroboter-Navigation: In automatisierten Lagern verlassen sich die Roboter auf A*, um effizient zwischen den Regalen zu navigieren, um Artikel zu entnehmen und zu platzieren, um Verzögerungen zu minimieren und Kollisionen mit anderen Robotern zu vermeiden.
• Drohnenflugbahnoptimierung: A* hilft Drohnen bei der Planung effizienter Flugrouten, sei es für Lieferungen, Vermessungen oder für den Freizeitgebrauch, und stellt sicher, dass sie Hindernisse vermeiden und optimalen Routen folgen.
• Planung der Bewegungen von Fertigungsrobotern: In Fabriken wird A* eingesetzt, um sicherzustellen, dass sich die Roboter nahtlos zwischen den Arbeitsplätzen bewegen können, um Kollisionen mit anderen Maschinen zu vermeiden und die Produktivität zu erhalten.

4. Netzwerk-Systeme

A* wird auch bei der Optimierung des Netzwerkbetriebs eingesetzt, wo die Effizienz der Ressourcennutzung und des Routings im Vordergrund steht.

• Netzwerk-Paket-Routing: A* wird verwendet, um den effizientesten Weg für Datenpakete durch ein Netzwerk zu bestimmen und so minimale Latenzzeiten und hohe Zuverlässigkeit zu gewährleisten.
• Ressourcenzuweisung in verteilten Systemen: A* hilft bei der Optimierung der Ressourcenzuweisung und ermöglicht es verteilten Systemen, Aufgaben effizient auf verschiedene Knotenpunkte zu verteilen und gleichzeitig den Overhead zu minimieren.
• Leiterplatten-Pfaddesign: Beim Entwurf von Leiterplatten (PCBs) kann A* verwendet werden, um die optimalen Pfade für elektrische Leiterbahnen zu bestimmen und so minimale Störungen und ein effizientes Layout zu gewährleisten.
• Optimierung der Netzwerkkabelverlegung: A* wird bei der Planung physischer Netzwerkinfrastrukturen eingesetzt, um die effektivsten Routen für Kabel zu finden und so die Kosten zu minimieren und die Leistung zu maximieren.

Was A* besonders wertvoll macht, ist seine Anpassungsfähigkeit durch benutzerdefinierte heuristische Funktionen, die eine Optimierung für verschiedene Metriken wie Entfernung, Zeit oder Energieverbrauch ermöglichen.

Im nächsten Abschnitt sehen wir uns einige häufige Herausforderungen und Optimierungstechniken an, um A* effektiv umzusetzen.

Gemeinsame Herausforderungen und Optimierungstechniken

A* ist zwar sehr leistungsfähig, aber um es effektiv umzusetzen, müssen mehrere gemeinsame Herausforderungen bewältigt werden. Die größte Hürde für Entwickler ist die effiziente Verwaltung von Ressourcen, insbesondere bei großen Suchräumen.

Zu den wichtigsten Herausforderungen gehören:

• Speicherverbrauch in großen Graphen
• Leistungsengpässe bei komplexen Heuristiken
• Umgang mit unentschiedenen Situationen
• Abwägen zwischen Genauigkeit und Berechnungsgeschwindigkeit

Zum Glück gibt es mehrere effektive Optimierungsstrategien, um diese Herausforderungen zu meistern:

• Bei der Speicherverwaltung solltest du dich auf effiziente Datenstrukturen
• Verwende binäre Heaps für die offene Liste anstelle von Arrays
• Implementiere eine Hash-Tabelle für schnellere Nachforschungen in geschlossenen Listen
• Unnötige Knotendaten nach der Verarbeitung löschen

Wenn die Leistung entscheidend ist, solltest du diese Geschwindigkeitsverbesserungen in Betracht ziehen:

• Vereinfache heuristische Berechnungen wo möglich
• Ganzzahlige Arithmetik anstelle von Fließkommazahlen verwenden
• Implementiere hierarchisches Pathfinding für große Karten

Ein besonders effektiver Ansatz für große Räume ist die bilaterale Suche - die gleichzeitige Suche von Start und Ziel. Außerdem kannst du bei der gitterbasierten Pfadfindung die Leistung erheblich verbessern, indem du heuristische Werte vorberechnest oder Tabellen verwendest.

Denke daran, Optimierungsverfahren auf der Grundlage deiner spezifischen Anforderungen und Beschränkungen auszuwählen. Der Schlüssel liegt darin, die richtige Balance zwischen Speichernutzung und Rechengeschwindigkeit für deine Anwendung zu finden.

Fazit

Der A*-Algorithmus ist ein grundlegendes Werkzeug bei der Pfadfindung und bei Problemen mit der Durchquerung von Graphen. In diesem Leitfaden haben wir die Kernkonzepte kennengelernt, eine praktische Lösung in Python implementiert und die verschiedenen Anwendungsmöglichkeiten untersucht. Die Stärke des Algorithmus liegt in der Ausgewogenheit von Genauigkeit und Effizienz, was ihn in verschiedenen Bereichen von Spielen bis hin zur Robotik von unschätzbarem Wert macht.

Die Umsetzung von A* bringt zwar einige Herausforderungen mit sich, aber die besprochenen Optimierungstechniken können dir helfen, effiziente Lösungen zu finden. Wenn du Spiele entwickelst, Roboterpfade planst oder Routing-Probleme löst, dann bietet dir das Verständnis des A*-Algorithmus einen leistungsstarken Ansatz, um optimale Pfade in deinen Anwendungen zu finden

Die Entwicklung solch anspruchsvoller Algorithmen erfordert eine solide Grundlage in Python-Programmierkonzepten und Best Practices. Willst du deine Python-Grundlagen stärken und fortgeschrittene Algorithmen wie A* in Angriff nehmen? 

Bring deine Programmierkenntnisse auf die nächste Stufe mit unserem Mittelstufenkurs Python für Entwickler in dem du benutzerdefinierte Funktionen beherrschst, wichtige Module kennenlernst und anspruchsvolle Anwendungen erstellst.