O algoritmo A*: Um guia completo

Os algoritmos de travessia de gráficos são fundamentais para muitos aplicativos de ciência da computação, desde o desenvolvimento de jogos até a robótica. Esses algoritmos são projetados para explorar e navegar em gráficos, que são estruturas de dados compostas de nós (vértices) e bordas. Entre esses algoritmos, o algoritmo A* se destaca como uma abordagem particularmente eficiente e versátil para encontrar caminhos ideais.

O algoritmo A* é um algoritmo de busca informado, o que significa que ele utiliza uma função heurística para orientar sua busca em direção à meta. Essa função heurística estima o custo de alcançar a meta a partir de um determinado nó, permitindo que o algoritmo priorize caminhos promissores e evite explorar caminhos desnecessários.

Neste artigo, veremos os principais conceitos do algoritmo A*, sua implementação em Python, suas aplicações e suas vantagens e limitações.

Para saber mais sobre programação em Python, confira nosso Curso de introdução ao Python para desenvolvedores curso.

O que é o algoritmo A*?

O algoritmo A* é um algoritmo avançado e amplamente usado para atravessar gráficos e encontrar caminhos. Ele encontra o caminho mais curto entre um nó inicial e um nó de meta em um gráfico ponderado. 

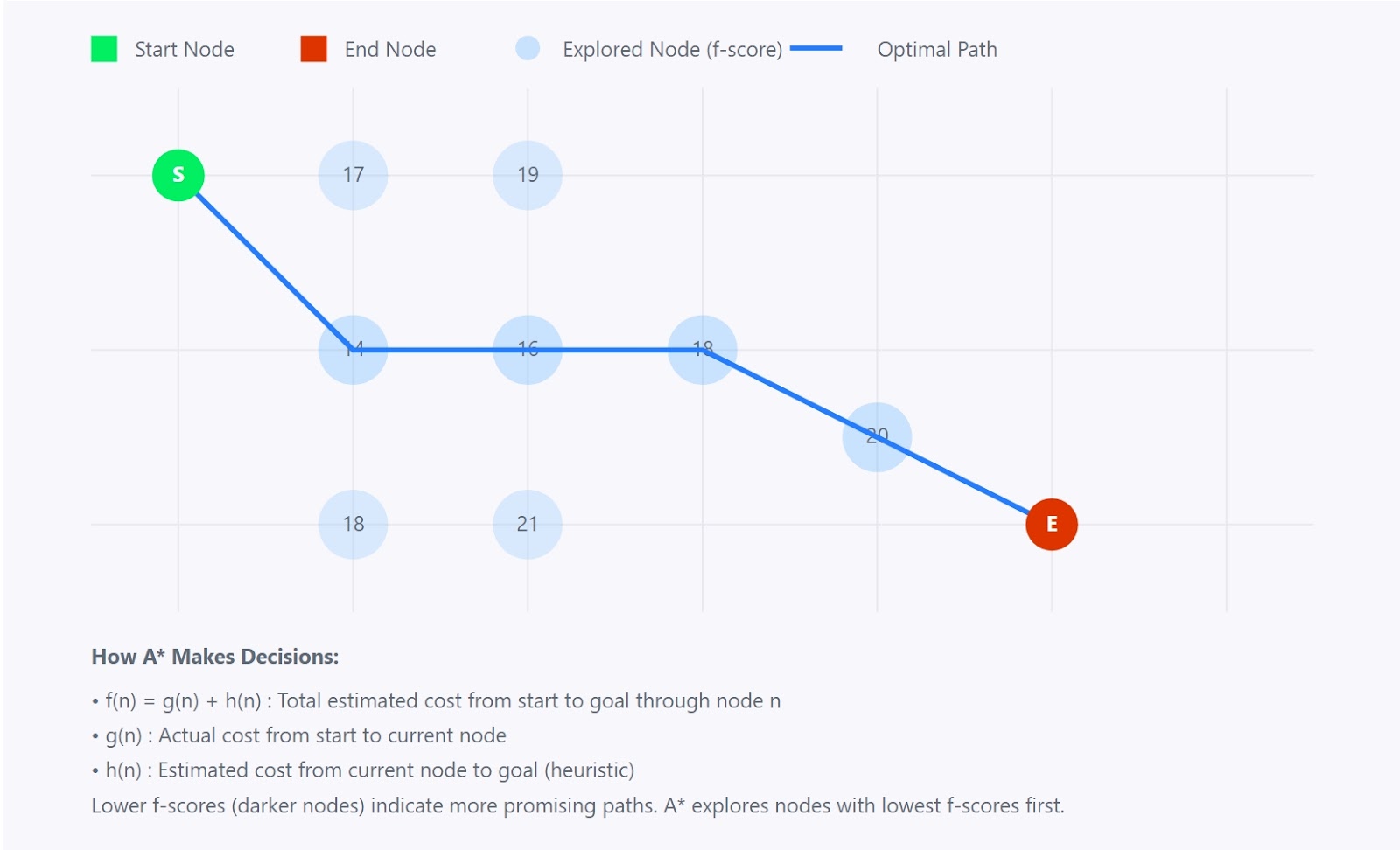
Algoritmo A*

Como funciona o algoritmo A*?

O algoritmo A* combina os melhores aspectos de dois outros algoritmos:

1. Algoritmo de Dijkstra: Esse algoritmo encontra o caminho mais curto para todos os nós a partir de um único nó de origem.
2. Busca de melhor primeiro com ganância: Esse algoritmo explora o nó que parece estar mais próximo da meta, com base em uma função heurística.

Imagine que você está tentando encontrar a rota mais curta entre duas cidades em um mapa. Enquanto o algoritmo de Dijkstra exploraria em todas as direções e a busca do melhor primeiro poderia ir direto para o destino (possivelmente perdendo atalhos), o A* faz algo mais inteligente. Ele considera ambos:

• A distância já percorrida desde o início
• Uma estimativa inteligente da distância restante até a meta

Essa combinação ajuda a A* a tomar decisões informadas sobre o próximo caminho a ser explorado, tornando-a eficiente e precisa.

Principais componentes

Para entender o algoritmo A*, você precisa estar familiarizado com esses conceitos fundamentais:

• Nós: Pontos em seu gráfico (como interseções em um mapa)
• Bordas: Conexões entre nós (como estradas que conectam cruzamentos)
• Custo do caminho: O custo real de deslocamento de um nó para outro
• Heurística: Um custo estimado de qualquer nó até a meta
• Espaço de pesquisa: A coleção de todos os caminhos possíveis a serem explorados

Na próxima seção, analisaremos mais detalhadamente esses conceitos e veremos como o A* os utiliza para encontrar caminhos ideais.

Conceitos-chave na pesquisa A*

A eficiência do algoritmo A* vem de sua avaliação inteligente de caminhos usando três componentes principais: g(n), h(n) e f(n). Esses componentes trabalham juntos para orientar o processo de busca em direção aos caminhos mais promissores.

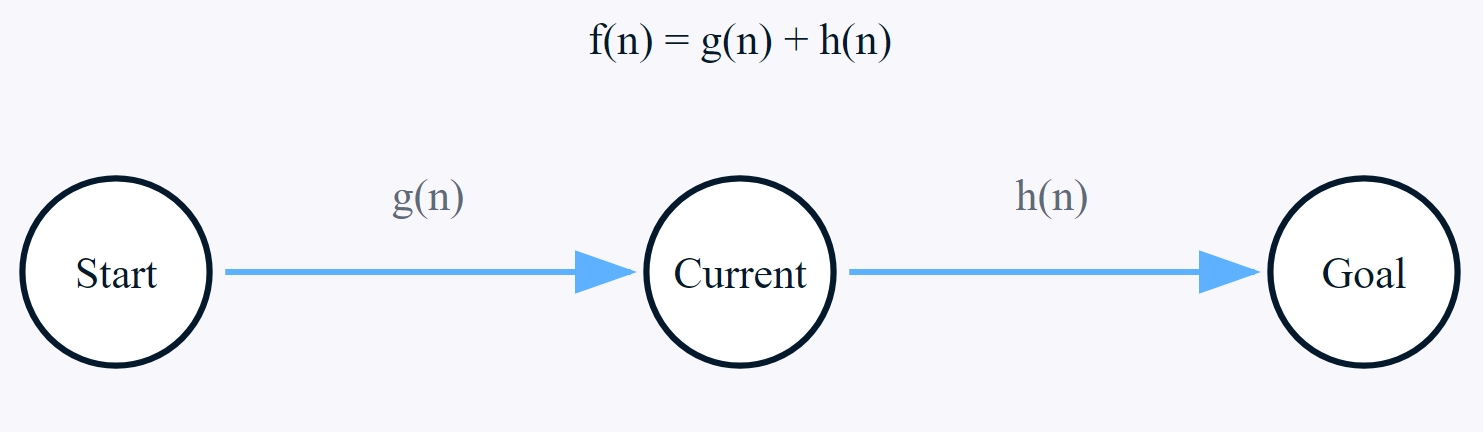
Função de custo do algoritmo A*

Compreensão das funções de custo

Custo do caminho g(n)

A função de custo do caminho g(n) representa a distância exata e conhecida do nó inicial até a posição atual em nossa pesquisa. Ao contrário dos valores estimados, esse custo é preciso e calculado pela soma de todos os pesos de borda individuais que foram percorridos ao longo do caminho escolhido. 

Matematicamente, para um caminho através dos nós n0(nó inicial) até nk​ (nó atual), podemos expressar g(n) como:

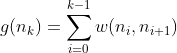
Onde:

• w(n_i,n_i+1) representa o peso da borda que conecta o nó ni ao nó n_i+1​.

À medida que avançamos no gráfico, esse valor se acumula, dando-nos uma medida clara dos recursos reais (seja distância, tempo ou qualquer outra métrica) que gastamos para chegar à nossa posição atual.

Função heurística h(n)

A função heurística h(n) fornece um custo estimado do nó atual até o nó de destino, atuando como o "palpite informado" do algoritmo sobre o caminho restante. 

Matematicamente, para qualquer nó n, a estimativa heurística deve satisfazer a condição h(n)≤h*(n) onde h*(n) é o custo real para a meta, tornando-o admissível por nunca superestimar o custo real.

Em problemas baseados em grade ou em mapas, as funções heurísticas comuns incluem distância de Manhattan e a Distância euclidiana. Para as coordenadas (x₁,y₁) do nó atual e (x₂,y₂) do nó de destino, essas distâncias são calculadas como:

Distância de Manhattan

Distância euclidiana

Custo total estimado f(n)

O custo total estimado f(n) é a pedra angular do processo de tomada de decisão do algoritmo A*, combinando o custo real do caminho e a estimativa heurística para avaliar o potencial de cada nó. Para qualquer nó n, esse custo é calculado como:

Onde:

• g(n) representa o custo real desde o início até o nó atual,
• h(n) representa o custo estimado do nó atual até a meta.

O algoritmo algoritmo usa esse valor combinado para escolher estrategicamente o próximo nó a ser explorado, sempre selecionando o nó com o menor valor de f(n) da lista aberta, garantindo assim um equilíbrio ideal entre os custos conhecidos e as distâncias restantes estimadas.

Gerenciamento de listas de nós

O algoritmo A* mantém duas listas essenciais

Lista aberta:

• Contém nós que precisam ser avaliados
• Ordenado pelo valor f(n) (o menor primeiro)
• Novos nós são adicionados à medida que são descobertos

Lista fechada:

• Contém nós já avaliados
• Ajuda a evitar a reavaliação de nós
• Usado para reconstruir o caminho final

O algoritmo seleciona continuamente o nó com o menor valor de f(n) da lista aberta, avalia-o e move-o para a lista fechada até atingir o nó de meta ou determinar que não há caminho.

Pseudocódigo do algoritmo de pesquisa A*

Agora que entendemos os componentes fundamentais do A*, vamos ver como eles se combinam na prática. A implementação do algoritmo pode ser dividida em etapas claras e lógicas que transformam esses conceitos em uma solução funcional de localização de caminhos.

Veja a seguir como o algoritmo funciona, passo a passo:

function A_Star(start, goal):
    // Initialize open and closed lists
    openList = [start]          // Nodes to be evaluated
    closedList = []            // Nodes already evaluated
    
    // Initialize node properties
    start.g = 0                // Cost from start to start is 0
    start.h = heuristic(start, goal)  // Estimate to goal
    start.f = start.g + start.h       // Total estimated cost
    start.parent = null              // For path reconstruction
    while openList is not empty:
        // Get node with lowest f value - implement using a priority queue
       // for faster retrieval of the best node
        current = node in openList with lowest f value
        
        // Check if we've reached the goal
        if current = goal:
            return reconstruct_path(current)
            
        // Move current node from open to closed list
        remove current from openList
        add current to closedList
        
        // Check all neighboring nodes
        for each neighbor of current:
            if neighbor in closedList:
                continue  // Skip already evaluated nodes
                
            // Calculate tentative g score
            tentative_g = current.g + distance(current, neighbor)
            
            if neighbor not in openList:
                add neighbor to openList
            else if tentative_g >= neighbor.g:
                continue  // This path is not better
                
            // This path is the best so far
            neighbor.parent = current
            neighbor.g = tentative_g
            neighbor.h = heuristic(neighbor, goal)
            neighbor.f = neighbor.g + neighbor.h
    
    return failure  // No path exists
function reconstruct_path(current):
    path = []
    while current is not null:
        add current to beginning of path
        current = current.parent
    return path

Vamos detalhar cada componente dessa implementação:

Fase de inicialização

O algoritmo começa com a configuração de duas listas essenciais:

• A lista aberta começa apenas com o nó inicial
• A lista fechada começa vazia

Cada nó armazena quatro informações essenciais:

• g: O custo real do nó inicial
• h: O custo estimado para a meta
• f: A soma de g e h
• pai: Referência ao nó anterior (para reconstrução do caminho)

Loop principal

O núcleo do A* é seu loop principal, que continua até que você tenha um dos dois:

• A meta é alcançada (sucesso)
• A lista aberta fica vazia (falha - não existe caminho)

Durante cada iteração, o algoritmo:

1. Seleciona o nó mais promissor (valor f mais baixo) da lista aberta
2. Move-o para a lista fechada
3. Examina todos os nós vizinhos

Avaliação do vizinho

Para cada vizinho, o algoritmo:

• Ignora os nós que já estão na lista fechada
• Calcula uma pontuação g provisória
• Atualiza os valores dos nós se for encontrado um caminho melhor
• Adiciona novos nós à lista aberta

Reconstrução de caminho

Quando a meta é atingida, o algoritmo trabalha de trás para frente por meio das referências pai para construir o caminho ideal do início até a meta.

Essa abordagem sistemática garante que A* sempre encontrará o caminho ideal se:

1. A função heurística é admissível (nunca superestima)
2. Existe de fato um caminho entre os nós de início e de meta

Na próxima seção, traduziremos esse pseudocódigo em uma implementação prática em Python, completa com visualizações para ajudar você a entender como o algoritmo explora o espaço de busca.

Implementação em Python do algoritmo A*

Agora que entendemos a teoria e o pseudocódigo, vamos implementar o A* em Python. Criaremos uma implementação prática que você poderá usar como base para seus próprios projetos. Para tornar isso concreto, implementaremos o algoritmo em uma grade 2D - um cenário comum em jogos e aplicativos de robótica.

Etapa 1: Funções essenciais e importações

Primeiramente, importamos as bibliotecas necessárias e criamos uma estrutura de nós que armazenará informações de posição e localização para cada ponto em nosso espaço de pesquisa.

from typing import List, Tuple, Dict, Set
import numpy as np
import heapq
from math import sqrt
def create_node(position: Tuple[int, int], g: float = float('inf'), 
                h: float = 0.0, parent: Dict = None) -> Dict:
    """
    Create a node for the A* algorithm.
    
    Args:
        position: (x, y) coordinates of the node
        g: Cost from start to this node (default: infinity)
        h: Estimated cost from this node to goal (default: 0)
        parent: Parent node (default: None)
    
    Returns:
        Dictionary containing node information
    """
    return {
        'position': position,
        'g': g,
        'h': h,
        'f': g + h,
        'parent': parent
    }

Etapa 2: Funções auxiliares

Para dar suporte ao nosso algoritmo de pathfinding, criaremos várias funções auxiliares. Primeiro, implementaremos uma função para calcular as distâncias entre os pontos usando a distância euclidiana.

Em seguida, adicionaremos uma função para encontrar posições vizinhas válidas em nossa grade, verificando cuidadosamente os limites e os obstáculos. Por fim, criaremos uma função que nos ajudará a reconstruir o caminho depois de encontrarmos nosso objetivo.

def calculate_heuristic(pos1: Tuple[int, int], pos2: Tuple[int, int]) -> float:
    """
    Calculate the estimated distance between two points using Euclidean distance.
    """
    x1, y1 = pos1
    x2, y2 = pos2
    return sqrt((x2 - x1)**2 + (y2 - y1)**2)
def get_valid_neighbors(grid: np.ndarray, position: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Get all valid neighboring positions in the grid.
    
    Args:
        grid: 2D numpy array where 0 represents walkable cells and 1 represents obstacles
        position: Current position (x, y)
    
    Returns:
        List of valid neighboring positions
    """
    x, y = position
    rows, cols = grid.shape
    
    # All possible moves (including diagonals)
    possible_moves = [
        (x+1, y), (x-1, y),    # Right, Left
        (x, y+1), (x, y-1),    # Up, Down
        (x+1, y+1), (x-1, y-1),  # Diagonal moves
        (x+1, y-1), (x-1, y+1)
    ]
    
    return [
        (nx, ny) for nx, ny in possible_moves
        if 0 <= nx < rows and 0 <= ny < cols  # Within grid bounds
        and grid[nx, ny] == 0                # Not an obstacle
    ]
def reconstruct_path(goal_node: Dict) -> List[Tuple[int, int]]:
    """
    Reconstruct the path from goal to start by following parent pointers.
    """
    path = []
    current = goal_node
    
    while current is not None:
        path.append(current['position'])
        current = current['parent']
        
    return path[::-1]  # Reverse to get path from start to goal

Etapa 3: Implementação do algoritmo A* principal

Agora vamos implementar nosso algoritmo. Usaremos uma fila de prioridades para garantir que sempre exploremos os caminhos mais promissores primeiro. 

Nosso algoritmo manterá dois conjuntos: um conjunto aberto para os nós que ainda precisamos explorar e um conjunto fechado para os nós que já verificamos. 

À medida que explorarmos a grade, atualizaremos continuamente os custos do caminho sempre que encontrarmos rotas melhores até atingirmos nosso objetivo.

def find_path(grid: np.ndarray, start: Tuple[int, int], 
              goal: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Find the optimal path using A* algorithm.
    
    Args:
        grid: 2D numpy array (0 = free space, 1 = obstacle)
        start: Starting position (x, y)
        goal: Goal position (x, y)
    
    Returns:
        List of positions representing the optimal path
    """
    # Initialize start node
    start_node = create_node(
        position=start,
        g=0,
        h=calculate_heuristic(start, goal)
    )
    
    # Initialize open and closed sets
    open_list = [(start_node['f'], start)]  # Priority queue
    open_dict = {start: start_node}         # For quick node lookup
    closed_set = set()                      # Explored nodes
    
    while open_list:
        # Get node with lowest f value
        _, current_pos = heapq.heappop(open_list)
        current_node = open_dict[current_pos]
        
        # Check if we've reached the goal
        if current_pos == goal:
            return reconstruct_path(current_node)
            
        closed_set.add(current_pos)
        
        # Explore neighbors
        for neighbor_pos in get_valid_neighbors(grid, current_pos):
            # Skip if already explored
            if neighbor_pos in closed_set:
                continue
                
            # Calculate new path cost
            tentative_g = current_node['g'] + calculate_heuristic(current_pos, neighbor_pos)
            
            # Create or update neighbor
            if neighbor_pos not in open_dict:
                neighbor = create_node(
                    position=neighbor_pos,
                    g=tentative_g,
                    h=calculate_heuristic(neighbor_pos, goal),
                    parent=current_node
                )
                heapq.heappush(open_list, (neighbor['f'], neighbor_pos))
                open_dict[neighbor_pos] = neighbor
            elif tentative_g < open_dict[neighbor_pos]['g']:
                # Found a better path to the neighbor
                neighbor = open_dict[neighbor_pos]
                neighbor['g'] = tentative_g
                neighbor['f'] = tentative_g + neighbor['h']
                neighbor['parent'] = current_node
    
    return []  # No path found

Etapa 4: Visualização

Agora, vamos criar uma função de visualização. Isso nos mostrará o layout da grade com todos os obstáculos, desenhará o caminho ideal calculado e marcará claramente as posições de início e meta.

import matplotlib.pyplot as plt
def visualize_path(grid: np.ndarray, path: List[Tuple[int, int]]):
    """
    Visualize the grid and found path.
    """
    plt.figure(figsize=(10, 10))
    plt.imshow(grid, cmap='binary')
    
    if path:
        path = np.array(path)
        plt.plot(path[:, 1], path[:, 0], 'b-', linewidth=3, label='Path')
        plt.plot(path[0, 1], path[0, 0], 'go', markersize=15, label='Start')
        plt.plot(path[-1, 1], path[-1, 0], 'ro', markersize=15, label='Goal')
    
    plt.grid(True)
    plt.legend(fontsize=12)
    plt.title("A* Pathfinding Result")
    plt.show()

Exemplo de uso

Veja como você pode usar a implementação:

# Create a sample grid
grid = np.zeros((20, 20))  # 20x20 grid, all free space initially
# Add some obstacles
grid[5:15, 10] = 1  # Vertical wall
grid[5, 5:15] = 1   # Horizontal wall
# Define start and goal positions
start_pos = (2, 2)
goal_pos = (18, 18)
# Find the path
path = find_path(grid, start_pos, goal_pos)
if path:
    print(f"Path found with {len(path)} steps!")
    visualize_path(grid, path)
else:
    print("No path found!")

Saída

Caminho encontrado com 22 passos!

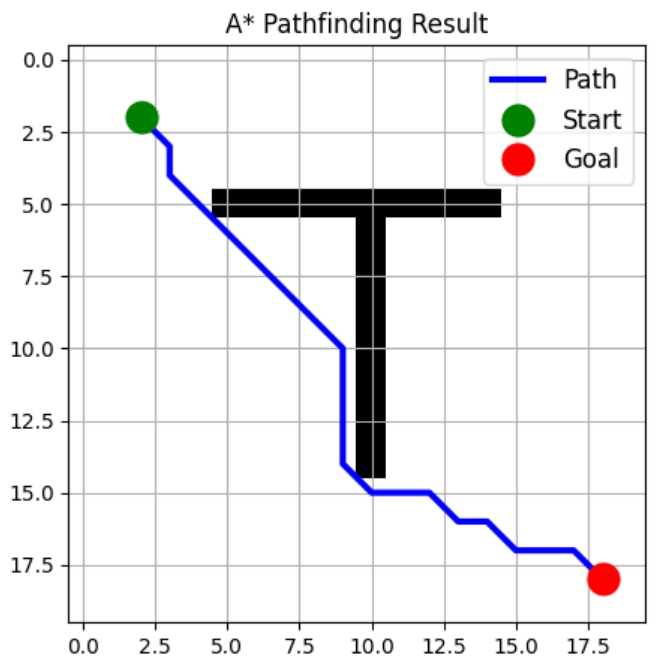
Essa implementação é eficiente e extensível. Você pode modificá-lo facilmente para:

• Usar diferentes funções heurísticas
• Suporte a diferentes tipos de movimento
• Manusear grades ponderadas
• Incluir restrições adicionais

Na próxima seção, examinaremos algumas aplicações práticas desse algoritmo e veremos como ele é usado em cenários do mundo real.

Aplicações do algoritmo de pesquisa A*

A eficiência e a flexibilidade do algoritmo A* o tornam valioso em vários domínios. Aqui estão as principais áreas em que ele se destaca:

1. Videogames e entretenimento

O algoritmo de busca A* é amplamente usado no desenvolvimento de videogames devido aos seus recursos ideais de localização de caminhos. Ele aprimora a experiência do jogador ao permitir movimentos mais realistas e responsivos dos personagens.

• Caminho do personagem em jogos de estratégia: O A* ajuda os personagens a encontrar o caminho mais curto ou mais seguro para um alvo, o que é crucial em jogos de estratégia em tempo real (RTS) em que as unidades precisam contornar obstáculos e inimigos com eficiência.
• Movimento de NPCs em ambientes de mundo aberto: Os personagens não jogáveis (NPCs) usam o A* para navegar em mundos de jogo grandes e dinâmicos, permitindo que eles atinjam objetivos enquanto evitam obstáculos e outros personagens.
• Planejamento tático em tempo real em cenários de combate: A* é usado para calcular o movimento e o posicionamento eficientes das unidades durante o combate, garantindo que os personagens possam chegar rapidamente a pontos vantajosos e evitar o perigo.
• Resolução de labirintos em jogos de quebra-cabeça: O A* é um algoritmo eficaz para navegar em labirintos complexos, oferecendo aos jogadores um desafio envolvente ao capacitar oponentes dinâmicos de resolução de labirintos ou fornecer dicas.

2. Sistemas de navegação

O A* é amplamente usado em sistemas de navegação para otimizar rotas, levando em conta vários fatores, como distância e possíveis obstáculos.

• Planejamento de rotas em aplicativos GPS: O A* encontra a rota mais curta e mais rápida entre dois pontos, tornando-o um componente essencial do software de GPS usado por milhões de pessoas em todo o mundo.
• Serviços de navegação com reconhecimento de tráfego: Nos aplicativos de navegação modernos, o A* é combinado com dados de tráfego em tempo real para sugerir a melhor rota, minimizando o tempo de viagem e evitando estradas congestionadas.
• Otimização de rotas de transporte público: O A* pode ajudar a encontrar rotas ideais que incorporem vários modos de transporte público, garantindo que os usuários façam transferências eficientes.
• Sistemas de navegação interna: O A* também é usado na navegação interna, como em aeroportos ou grandes shopping centers, onde ajuda a orientar os usuários em ambientes complexos com vários níveis e obstáculos.

3. Robótica e automação

O algoritmo A* é fundamental para a robótica, onde o movimento eficiente é essencial para a produtividade e a segurança.

• Planejamento autônomo do caminho do veículo: Os carros autônomos usam o A* para navegar pelas estradas, tomando decisões em tempo real sobre como ir do ponto A ao ponto B, evitando colisões e obedecendo às regras de trânsito.
• Navegação de robôs de armazém: Em armazéns automatizados, os robôs contam com o A* para navegar de forma eficiente entre as prateleiras de armazenamento para coletar e colocar itens, minimizando atrasos e evitando colisões com outros robôs.
• Otimização da trajetória de voo do drone: O A* ajuda os drones a planejar trajetórias de voo eficientes, seja para entrega, levantamento ou uso recreativo, garantindo que eles evitem obstáculos e sigam rotas ideais.
• Planejamento do movimento do robô de fabricação: Nas configurações de fábrica, o A* é usado para garantir que os robôs possam se mover sem problemas entre as estações de trabalho, evitando colisões com outras máquinas e mantendo a produtividade.

4. Sistemas de rede

O A* também é aplicado na otimização de operações de rede, em que a eficiência na utilização de recursos e no roteamento é fundamental.

• Roteamento de pacotes de rede: O A* é usado para determinar o caminho mais eficiente para os pacotes de dados percorrerem uma rede, garantindo latência mínima e alta confiabilidade.
• Alocação de recursos em sistemas distribuídos: O A* ajuda a otimizar a alocação de recursos, permitindo que os sistemas distribuídos aloquem tarefas de forma eficiente em vários nós e, ao mesmo tempo, minimizem a sobrecarga.
• Projeto do caminho da placa de circuito: Ao projetar placas de circuito impresso (PCBs), o A* pode ser usado para determinar os caminhos ideais para os traços elétricos, garantindo o mínimo de interferência e um layout eficiente.
• Otimização do roteamento de cabos de rede: O A* é empregado no projeto de infraestruturas de redes físicas, encontrando as rotas mais eficazes para os cabos a fim de minimizar o custo e maximizar o desempenho.

O que torna o A* particularmente valioso é sua capacidade de adaptação por meio de funções heurísticas personalizadas, permitindo a otimização de diferentes métricas, como distância, tempo ou uso de energia.

Na próxima seção, veremos alguns desafios comuns e técnicas de otimização para implementar o A* de forma eficaz.

Desafios comuns e técnicas de otimização

Embora o A* seja poderoso, para implementá-lo de forma eficaz, você precisa enfrentar vários desafios comuns. O maior obstáculo que os desenvolvedores enfrentam é o gerenciamento eficiente dos recursos, principalmente quando lidam com grandes espaços de pesquisa.

Os principais desafios incluem:

• Consumo de memória em gráficos grandes
• Gargalos de desempenho com heurística complexa
• Como lidar com situações de desempate
• Equilíbrio entre precisão e velocidade de computação

Felizmente, existem várias estratégias de otimização eficazes para enfrentar esses desafios:

• Para o gerenciamento de memória, concentre-se em estruturas de dados eficientes estruturas de dados
• Use heaps binários para a lista aberta em vez de matrizes
• Implementar uma tabela de hash para pesquisas mais rápidas em listas fechadas
• Limpar dados de nó desnecessários após o processamento

Quando o desempenho for fundamental, considere essas melhorias de velocidade:

• Simplificar os cálculos heurísticos sempre que possível
• Usar aritmética de números inteiros em vez de ponto flutuante
• Implementar o pathfinding hierárquico para mapas grandes

Uma abordagem particularmente eficaz para espaços grandes é a pesquisa bilateral - pesquisar a partir do início e da meta simultaneamente. Além disso, ao trabalhar com pathfinding baseado em grade, você pode melhorar significativamente o desempenho pré-computando valores heurísticos ou usando tabelas de pesquisa.

Lembre-se de escolher as técnicas de otimização com base em seus requisitos e restrições específicos. O segredo é encontrar o equilíbrio certo entre o uso da memória e a velocidade de computação para o seu aplicativo.

Conclusão

O algoritmo A* é uma ferramenta fundamental em problemas de localização de caminhos e travessia de gráficos. Neste guia, vimos seus principais conceitos, implementamos uma solução prática em Python e examinamos suas diversas aplicações. A força do algoritmo está em seu equilíbrio entre precisão e eficiência, o que o torna inestimável em vários domínios, desde jogos até robótica.

Embora a implementação do A* tenha seus desafios, as técnicas de otimização que discutimos podem ajudar você a criar soluções eficientes. Se você estiver desenvolvendo jogos, planejando caminhos de robôs ou resolvendo problemas de roteamento, a compreensão do algoritmo A* oferece uma abordagem poderosa para encontrar caminhos ideais em seus aplicativos

Para criar algoritmos tão sofisticados, você precisa de uma base sólida de conceitos e práticas recomendadas de programação em Python. Você deseja fortalecer suas bases em Python e lidar com algoritmos mais avançados, como o A*? 

Leve suas habilidades de programação para o próximo nível com nosso Curso Python Intermediário para Desenvolvedores no qual você dominará as funções personalizadas, explorará os módulos essenciais e criará aplicativos sofisticados.