Tutorial del Optimizador Adam: Intuición e implementación en Python

¿Qué es el Optimizador Adam? La respuesta breve

Adam, que significa Estimación Adaptativa de Momentos, es un popular algoritmo de optimización utilizado en el aprendizaje automático y, con mayor frecuencia, en el aprendizaje profundo. 

Adam combina las ideas principales de otras dos técnicas de optimización robusta: momentum y RMSprop. Se denomina adaptativo porque ajusta la tasa de aprendizaje para cada parámetro.

Aquí tienes sus principales características y ventajas:

• Adaptabilidad: Adam adapta el ritmo de aprendizaje para cada parámetro, lo que puede acelerar el aprendizaje en muchos casos.
• Impulso: Utiliza una forma de impulso, que le ayuda a navegar por superficies complejas, como barrancos y puntos de monte, con mayor eficacia.
• Corrección del sesgo: Adam incluye términos de corrección del sesgo, que le ayudan a obtener buenos resultados incluso en las fases iniciales del entrenamiento.
• Eficiencia computacional: Es relativamente eficiente desde el punto de vista computacional y requiere poca memoria.
• Robustez de los hiperparámetros: Aunque puede ser necesario ajustar la tasa de aprendizaje, Adam suele ser menos sensible a la elección de hiperparámetros que otros optimizadores.

En resumen, Adam hace que los modelos aprendan de forma más eficiente ajustando continuamente la tasa de aprendizaje de cada parámetro y, en consecuencia, tiende a converger mucho más rápidamente que el descenso de gradiente estocástico estándar descenso por gradiente estocástico. Para muchas aplicaciones de aprendizaje profundo, es, por tanto, una opción sólida por defecto.

Algoritmos previos

Adam unifica ideas clave de algunos otros algoritmos de optimización críticos, reforzando sus ventajas y abordando al mismo tiempo sus defectos. Tendremos que revisarlos antes de comprender la intuición que hay detrás de Adam e implementarla en Python.

Analogía de optimización

Para comprender la intuición que hay detrás de estos algoritmos de optimización, continuemos con nuestra analogía de la introducción. 

Imagina que tienes los ojos vendados en una región complicada y montañosa. Se te ha encomendado la tarea de encontrar el punto más bajo de este terreno. La pendiente del terreno representa la función de pérdida de un modelo de aprendizaje automático. El punto global "más bajo" (mínimo global) es la solución óptima del sistema.

Ahora, unamos algunos puntos: Tu posición actual en el terreno representa el estado actual de los parámetros del modelo. La altura en cualquier punto representa el valor de pérdida de esos parámetros. La forma en que navegas también se corresponde con el ajuste de los parámetros del modelo en un sentido matemático.

Cada algoritmo de optimización es como una estrategia para navegar con éxito por el paisaje de este problema, guiando al solucionador sobre dónde dar el siguiente paso y cómo de grandes deben ser esos pasos. Algunos algoritmos escanean toda la zona antes de decidir el siguiente movimiento, mientras que otros se basan en información limitada para ser más rápidos. 

Sin embargo, otros algoritmos utilizan herramientas como el impulso y la adaptación del tamaño del paso; un buen solucionador sabe cuándo abrirse camino a través de un problema y cuándo aflojar.

Descenso Gradiente

El descenso gradiente es el santo grial de la optimización en el aprendizaje automático, ya que sienta las bases sobre las que se asientan muchos algoritmos.

Si utilizas el Descenso Gradiente (DG), palpa cuidadosamente toda la zona a tu alrededor (utilizando el conjunto de datos completo) antes de dar cada paso. Este examen minucioso te permite tomar decisiones muy precisas sobre qué camino es cuesta abajo, pero lleva mucho tiempo. Siempre te mueves en la dirección del descenso más pronunciado, lo que significa que te desplazarás constantemente hacia terrenos más bajos. Sin embargo, si llegas a una pequeña depresión (el mínimo local), podrías quedarte atascado allí, incapaz de detectar que hay un punto aún más bajo en otro lugar.

Características principales de GD:

• Utiliza todo el conjunto de datos para cada paso
• Consistente, pero potencialmente lento
• Puede atascarse en mínimos locales

Descenso Gradiente Estocástico (SGD)

En este escenario, vas deprisa y te falta tiempo para percibir toda la región que te rodea. En su lugar, comprueba sólo un punto al azar cerca de tus pies (un punto de datos). Esto hace que cada paso sea más rápido pero menos preciso. También puedes comprobar un pequeño lote de puntos, lo que se conoce como descenso de gradiente en mini lotes, que veremos más adelante. 

Tu trayectoria es más errática que la del descenso por pendiente; en realidad, a veces parece la trayectoria de un marinero borracho. Ocasionalmente puedes ir cuesta arriba. Este camino ruidoso podría ser en realidad la mayor ventaja: es muy probable que escapes de los mínimos locales. 

Pero a medida que te acercas al fondo, tienes que dar pasos más pequeños (disminuir el ritmo de aprendizaje) para evitar sobrepasar el punto más bajo.

Características principales del SGD:

• Utiliza sólo un punto de datos aleatorio para cada paso
• Iteraciones más rápidas pero un camino más ruidoso
• Puede escapar más fácilmente de los mínimos locales
• A menudo es necesario disminuir el ritmo de aprendizaje con el tiempo

Nota: En este punto, te recomiendo encarecidamente que leas nuestro artículo sobre GD y SGDya que cubre los detalles de estos dos algoritmos críticos con mucha más profundidad. También te ayudará a entender mejor la sección de codificación que viene.

SGD Con Impulso

Ahora estás sobre un monopatín entre las colinas. Cuando te empujas en una dirección, el impulso del monopatín te mantiene más o menos en movimiento en la misma dirección durante un rato. 

Este impulso es como una media móvil de tus direcciones pasadas. Te ayuda a superar pequeños baches y desniveles locales, e incluso puede ayudarte a encontrar un punto de menor elevación más adelante. 

Si llevas un tiempo moviéndote en una dirección, el impulso aumenta y vas más rápido. De este modo, podrás converger en el punto más bajo más rápidamente, sobre todo en terrenos con una pendiente descendente constante.

Características principales de SGD con Impulso:

• Acumula una media móvil de gradientes pasados
• Ayuda a superar las pequeñas variaciones locales
• Puede conducir a una convergencia más rápida

RMSprop (Propagación cuadrática media)

Piensa en tener un calzado de alta tecnología que pueda ajustar su agarre en función del terreno por el que caminas. Estas zapatillas siguen el gradiente del terreno en cada dirección, manteniendo una media exponencialmente decreciente de los gradientes al cuadrado. En las zonas donde la pendiente cambia mucho, las zapatillas te dan más agarre, permitiéndote dar pasos más pequeños y cuidadosos. En zonas más suaves con pendientes consistentes, las zapatillas te proporcionan zancadas más largas. 

Este "tamaño del paso" adaptable te ayuda a navegar con eficacia tanto por pendientes pronunciadas como poco pronunciadas, evitando que des un paso demasiado grande en una zona escarpada o demasiado pequeño en una zona llana.

Características principales de RMSprop:

• Índices de aprendizaje adaptativos para cada parámetro
• Divide el ritmo de aprendizaje por una media de gradientes al cuadrado que decae exponencialmente
• Ayuda a navegar por zonas de diferente pendiente

La intuición detrás de Adam Optimizer

Adam es como fusionar tu monopatín (momentum) con tus zapatillas adaptables (RMSprop) y añadir un sistema de navegación inteligente a la mezcla.

La parte del monopatín (impulso) te mantiene en la dirección general correcta. Esto significa que en las regiones cuesta abajo, suaves y consistentes, Adam te permite moverte rápidamente. En terrenos complicados y variables, te ayuda a mantener un ritmo constante pero prudente.

Las zapatillas adaptables (RMSprop) detectan por dónde vas y ajustan el agarre del monopatín. El sistema de navegación inteligente (corrección del sesgo) de Adam es especialmente importante al inicio de tu viaje, cuando partes de un punto aleatorio y no sabes mucho sobre el terreno.

Esta combinación de atributos es la razón por la que Adam suele encontrar el punto más bajo (la solución al problema) de forma muy eficaz y por la que su estructura puede manejar bien distintos tipos de terreno (distintos tipos de problemas de aprendizaje automático).

Características principales de Adán:

• Combina ideas tanto de momentum como de RMSprop
• Mantiene una media exponencialmente decreciente de los gradientes pasados y de los gradientes pasados al cuadrado
• Índices de aprendizaje adaptativos para cada parámetro
• Corrección del sesgo de los pasos iniciales

Como has observado, cada uno de los algoritmos mencionados se basa en los anteriores, con el objetivo de optimizar el proceso de encontrar el punto más bajo abordando diferentes retos que se encuentran en varios tipos de problemas de optimización.

Adán Vs. Otros algoritmos de optimización

Antes de entrar en los detalles de la aplicación de Adam y de los otros algoritmos mencionados, permíteme compartir contigo una tabla resumen en la que se comparan el tiempo de ejecución y el rendimiento RMSE de cada uno de ellos en un problema de regresión de muestra:

import pandas as pd
# Disable scientific notation
pd.set_option("display.float_format", "{:.4f}".format)
comparison_table = pd.read_csv('optimization_results.csv')
comparison_table

Esta tabla no hace justicia a la enorme diferencia entre Adán y el resto, así que permíteme que elabore un gráfico de barras:

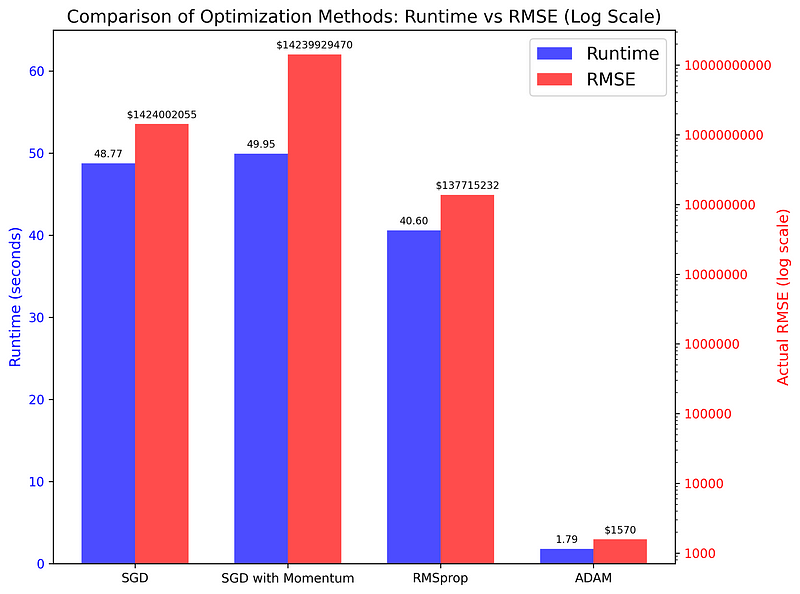
El gráfico compara el tiempo de ejecución y las puntuaciones RMSE de los cuatro algoritmos utilizados en una tarea de regresión simple. Como puedes ver, las diferencias son asombrosas (recuerda que el eje de la derecha está en una escala logarítmica), lo que indica que Adam es la opción superior para la mayoría de las tareas de optimización.

Más adelante veremos el código que generó la tabla y el gráfico.

Implementación del optimizador Adam en Python

Ahora que hemos cubierto los conceptos necesarios para Adán y su intuición, podemos empezar a implementarlos en Python. A lo largo del camino, explicaremos cualquier cálculo matemático necesario para comprender la puesta en práctica. Construiremos el código paso a paso, empezando por el Descenso Gradiente Estocástico.

Implantar SGD con minilotes

Antes hemos mencionado que la SGD utiliza un único punto de datos para decidir hacia dónde moverse a continuación. En la práctica, esta versión vainilla del SGD se utiliza poco, ya que sus resultados pueden ser ruidosos (su trayectoria en las colinas es errática). 

Para mitigarlo, los profesionales suelen utilizar una variante llamada Mini-lote de Descenso Gradiente que utiliza lotes de puntos de datos, como 32, 64 o 128, antes de dar cada paso (esto es como escanear un camino estrecho en lugar de la vista de 360 grados antes de dar un paso). 

Por lo tanto, construiremos el código fundacional de Adam con esta versión de SGD.

Para que el código sea lo más sencillo posible, elegiremos un pequeño problema de regresión: predecir los precios de los diamantes dadas sus medidas en quilates.

Primero vamos a importar las bibliotecas necesarias:

import seaborn as sns
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
np.random.seed(42)

A continuación, cargamos el conjunto de datos Diamonds de Seaborn, tomamos una muestra de él y construimos las matrices de características y objetivos:

# Load the data
dataset_size = 20_000
diamonds = sns.load_dataset("diamonds")
# Extract the target and the feature
xy = diamonds[["carat", "price"]].values
np.random.shuffle(xy)  # Shuffle the data
xy = xy[:dataset_size]
xy.shape

Output:
(20000, 2)

La regresión lineal requiere que normalicemos los datos:

# Normalize the data
mean = np.mean(xy, axis=0)
std = np.std(xy, axis=0)
xy_normalized = (xy - mean) / std

Ahora, podemos dividir los datos para crear conjuntos de entrenamiento y de prueba:

# Split the data
train_size = int(0.8 * dataset_size)
train_xy, test_xy = xy[:train_size], xy[train_size:]
train_xy.shape

(16000, 2)

Para resolver la tarea, tenemos una serie de modelos a nuestra disposición, pero para simplificar las cosas, elegiremos la Regresión Lineal Simple y la definiremos como una función:

def model(m, x, b):
   """
   Simple Linear Regression: f(x) = m * x + b, where
   - x: diamond carat
   - m: price increase per carat
   - b: base diamond price
   - f(x): predicted diamond price
   """
  
   return m * x + b

Nuestro modelo de Regresión Lineal sólo tiene dos parámetros, m y bpor lo que la tarea de SGD (y más tarde, de Adam) es encontrar los valores óptimos para ellos.

También debemos definir la función de pérdida, Error Cuadrático Medio, que minimizarán nuestros algoritmos:

def mean_squared_error(y_true, y_pred):
   """
   MSE as a loss function. It is defined as:
   Loss = (1/n) * Σ((y - f(x))²), where:
   - n: the length of the dataset
   - y: the true diamond price
   - f(x): predicted diamond price, i.e. m*x + b
   """
   return np.mean((y_true - y_pred) ** 2)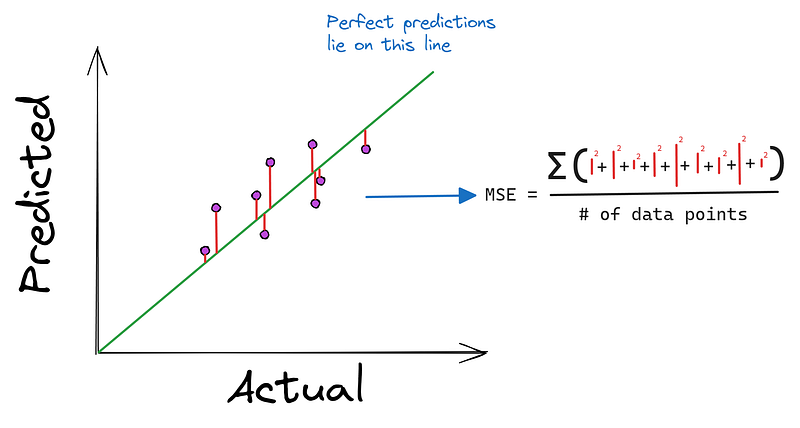

Ahora definimos una función llamada stochastic_gradient_descent que acepta seis argumentos:

• x y y representan la característica única y el objetivo en nuestro problema.
• epochs indica cuántas veces queremos realizar el descenso (más adelante hablaremos de ello).
• learning_rate es el tamaño del paso.
• batch_size para controlar la frecuencia con la que actualizamos los parámetros
• stopping_threshold fija el valor mínimo al que debe disminuir la pérdida en cada paso

def stochastic_gradient_descent(
   x, y, epochs=100, learning_rate=0.01, batch_size=32, stopping_threshold=1e-6
):
   """
   SGD with support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   n = len(x)  # The number of data points
   previous_loss = np.inf

Dentro de la función, primero inicializamos los parámetros que queremos optimizar con valores aleatorios (empezando en un lugar aleatorio de las colinas). También fijamos la pérdida inicial en infinito, lo que representa el estado no resuelto de nuestro problema.

A continuación, iniciamos un bucle for que se ejecuta durante epochs iteraciones. Dentro del bucle, barajamos los datos para evitar el aprendizaje de patrones dependientes del orden en los datos:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       # Shuffle the data
       indices = np.random.permutation(n)
       x = x[indices]
       y = y[indices]

A continuación, iniciamos otro bucle controlado por el parámetro batch_size y extraemos el lote actual:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           x_batch = x[j:j + batch_size]
           y_batch = y[j:j + batch_size]

Dentro de este bucle interno, calculamos los gradientes (derivadas parciales) de ambos parámetros (indicando dónde tenemos que dar el siguiente paso):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Make predictions with current m, b
           y_pred = model(m, x_batch, b)
           # Compute the gradients
           m_gradient = 2 * np.mean(x_batch * (y_batch - y_pred))
           b_gradient = 2 * np.mean(y_batch - y_pred)

Después de calcular los gradientes, hay un paso crítico de recorte de los gradientes:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           clip_value = 1.0
           m_gradient = np.clip(m_gradient, -clip_value, clip_value)
           b_gradient = np.clip(b_gradient, -clip_value, clip_value)

El recorte de degradado evita la común gradientes explosivos en el que la magnitud de los gradientes va hacia el infinito.

Tras el recorte, actualizamos los parámetros utilizando la tasa de aprendizaje (damos un paso en la dirección de los gradientes controlados por la tasa de aprendizaje):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           m -= learning_rate * m_gradient
           b -= learning_rate * b_gradient

Ahora, en el bucle padre (una vez explorados todos los lotes), calculamos la pérdida de la época actual (mira cuánto hemos descendido desde nuestra posición inicial):

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       y_pred = model(m, x, b)
       current_loss = loss(y, y_pred)

Si la pérdida de época es menor que el stopping_thresholddetenemos todo el proceso:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       ...
       # Check against the stopping threshold
       if abs(previous_loss - current_loss) < stopping_threshold:
           break
       previous_loss = current_loss

Al final (después de que se agoten las épocas o se alcance el umbral de parada), devolvemos m y b, que ahora están optimizados:

def stochastic_gradient_descent(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update the model parameters
           ...
       # Compute the epoch loss
       ...
       # Check against the stopping threshold
       ...
   return m, b

SGD Con Impulso

Ahora, añadamos momentum a SGD. El código de esta versión no es muy diferente del de la versión mini-batch.

Definimos una nueva función con un momentum parámetro:

def stochastic_gradient_descent_with_momentum(
       x, y, epochs=100, learning_rate=0.01, batch_size=32,
       stopping_threshold=1e-6, momentum=0.9
):
   """
   SGD with momentum and support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   # Initialize velocity terms
   v_m = 0
   v_b = 0
  
   n = len(x)
   previous_loss = np.inf

Dentro de la función, definiremos dos variables más, v_m y v_b, para llevar la cuenta de los gradientes acumulados que nos servirán de impulso. Al principio los ponemos a 0, ya que no tenemos ningún impulso al inicio del algoritmo.

Luego, el resto del código es el mismo hasta después de recortar los degradados:

def sgd_with_momentum(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Gradient clipping
           ...
           # Update velocity terms
           v_m = momentum * v_m + learning_rate * m_gradient
           v_b = momentum * v_b + learning_rate * b_gradient
           # Update the model parameters using velocity
           m -= v_m
           b -= v_b

Una vez recortados los gradientes, utilizamos la regla de actualización del momento para modificar los términos de velocidad. Aquí tienes una vista superior del código:

# Initialize
v_m = 0
v_b = 0
...
# Update velocity terms
v_m = momentum * v_m + learning_rate * m_gradient
v_b = momentum * v_b + learning_rate * b_gradient
# Update the model parameters using velocity
m -= v_m
b -= v_b

La velocidad v_* acumula gradientes a lo largo del tiempo. Esto significa que si nos movemos en una dirección coherente, ganaremos velocidad en esa dirección.

En las zonas donde el gradiente cambia rápidamente (como los valles estrechos en el paisaje de pérdidas), el impulso ayuda a amortiguar las oscilaciones. Desarrollamos la inercia suficiente para no quedarnos atascados en pequeñas variaciones locales, como mínimos locales o puntos de silla.

La partemomentum * v_m es la que acumula los gradientes. Por ejemplo, si tenemos un gradiente positivo grande, entonces su velocidad será igualmente grande, y la actualización del parámetro será aún mayor. Así, un impulso de 0,9 significa que conservamos el 90% de la velocidad del cambio anterior para el paso siguiente. En cada paso N, utilizaremos el 90% de la velocidad total de los gradientes de los pasos N-1.

En este punto, te animo a que inventes algunos valores aleatorios para m y b y sus gradientes y utiliza la regla de actualización del impulso para ver cómo cambian los parámetros si vas cuesta arriba o cuesta abajo.

RMSprop

Ahora, veamos la implementación de RMSprop. Al igual que la SGD con el impulso, el mayor cambio se produce al actualizar los parámetros.

En primer lugar, definimos una nueva función con dos parámetros adicionales beta y epsilon (sin impulso):

def rmsprop_optimization(
   x, y, epochs=100, learning_rate=0.01, batch_size=32,
   stopping_threshold=1e-6, beta=0.9, epsilon=1e-8,
):
   """
   RMSprop optimization with support for mini-batches.
   """
   # Initialize the model parameters randomly
   m = np.random.randn()
   b = np.random.randn()
   # Initialize accumulators for squared gradients
   s_m = 0
   s_b = 0
   n = len(x)
   previous_loss = np.inf

Además, dentro de la función, creamos dos nuevas variables para acumular gradientes al cuadrado, s_m y s_b.

Ahora, cuando llegamos a la fase de actualización, volvemos a calcular los gradientes al cuadrado y luego actualizamos los parámetros:

def rmsprop_optimization(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # RMSprop doesn't need gradient clipping
           # Update accumulators
           s_m = beta * s_m + (1 - beta) * (m_gradient**2)
           s_b = beta * s_b + (1 - beta) * (b_gradient**2)
           # Update parameters
           m -= learning_rate * m_gradient / (np.sqrt(s_m) + epsilon)
           b -= learning_rate * b_gradient / (np.sqrt(s_b) + epsilon)
           # The rest of the code is the same

Aquí vemos dos nuevos parámetros en uso:

• epsilon es un valor pequeño, normalmente 1e-8, para evitar la división por cero al realizar actualizaciones.
• beta es el parámetro de la velocidad de desintegración, normalmente en torno a 0,9.

El parámetrobeta controla cuánta historia tenemos en cuenta. Una beta más alta significa que adoptamos una visión a más largo plazo de los gradientes pasados, mientras que una beta más baja hace que el algoritmo responda más a los gradientes recientes.

No necesitas preocuparte por las matemáticas que hay detrás de la regla de actualización de RMSprop. Lo importante es la lógica que hay detrás.

En esencia, lo que hacen las cuatro líneas anteriores es

1. Adaptar la tasa de aprendizaje para cada parámetro, lo cual es crucial, ya que distintos parámetros pueden requerir distintas tasas de aprendizaje.
2. Manejar el problema del "gradiente evanescente", común en las redes neuronales en las que los gradientes se hacen demasiado pequeños debido a la retropropagación. Este efecto se mitiga normalizando los gradientes.
3. Equilibrar el tamaño del paso:

• Para los parámetros con gradientes grandes (actualizados con frecuencia), la suma del gradiente al cuadrado en el denominador será grande, lo que reducirá la tasa de aprendizaje efectiva.
• Para los parámetros con gradientes pequeños (actualizados con poca frecuencia), el denominador será menor, aumentando la tasa de aprendizaje efectiva.

En la práctica, el RMSprop suele funcionar mejor que el SGD básico o el SGD con impulso, sobre todo para los problemas de optimización no convexos que suelen darse en el aprendizaje profundo.

La Implementación Final: Adán en Python

De nuevo, definimos una nueva función:

def adam_optimization(
   x,
   y,
   epochs=100,
   learning_rate=0.001,
   batch_size=32,
   stopping_threshold=1e-6,
   beta1=0.9,
   beta2=0.999,
   epsilon=1e-8,
):
   """
   Adam optimization with support for mini-batches.
   """
   # Initialize the model parameters
   m = np.random.randn()
   b = np.random.randn()
   # Initialize first and second moment vectors
   m_m, v_m = 0, 0
   m_b, v_b = 0, 0
   n = len(x)
   previous_loss = np.inf
   t = 0  # Initialize timestep

Esta vez, definimos cinco nuevas variables para capturar los vectores de primer y segundo momento y el paso del tiempo. En el contexto de Adán:

1. El vector del primer momento (m):

• Es una estimación de la media (primer momento) de los gradientes.
• Calculada como una media exponencialmente decreciente de los gradientes anteriores.
• Ayuda a estimar la dirección del gradiente.

2. El vector del segundo momento (v):

• Es una estimación de la varianza no centrada (segundo momento) de los gradientes.
• También se calcula como una media que decae exponencialmente, pero de gradientes al cuadrado.
• Ayuda a adaptar el ritmo de aprendizaje de cada parámetro.

Entonces, el código sigue siendo el mismo hasta después de calcular los degradados (no necesitamos recortarlos para Adam):

def adam_optimization(...):
   ...
   for i in range(epochs):
       ...
       for j in range(0, n, batch_size):
           # Extract the current batch
           ...
           # Compute the gradients
           ...
           # Adam doesn't need gradient clipping
          
           # Update biased first moment estimate
           m_m = beta1 * m_m + (1 - beta1) * m_gradient
           m_b = beta1 * m_b + (1 - beta1) * b_gradient
           # Update biased second raw moment estimate
           v_m = beta2 * v_m + (1 - beta2) * (m_gradient**2)
           v_b = beta2 * v_b + (1 - beta2) * (b_gradient**2)
           # Compute bias-corrected first moment estimate
           m_m_hat = m_m / (1 - beta1**t)
           m_b_hat = m_b / (1 - beta1**t)
           # Compute bias-corrected second raw moment estimate
           v_m_hat = v_m / (1 - beta2**t)
           v_b_hat = v_b / (1 - beta2**t)
           # Update parameters
           m -= learning_rate * m_m_hat / (np.sqrt(v_m_hat) + epsilon)
           b -= learning_rate * m_b_hat / (np.sqrt(v_b_hat) + epsilon)
       # The rest of the code is the same

De nuevo, te pido que no te preocupes por estas líneas de código, ya que implican demasiadas matemáticas. En la práctica, nunca tendrás que implementar Adán desde cero, porque todo lo que necesitas saber es la intuición que hay detrás de su regla de actualización.

El primer momento actúa como un impulso, acumulando gradientes pasados para dar a la optimización una sensación de dirección y velocidad. Esto ayuda a Adam a moverse más rápido en direcciones consistentes y amortigua las oscilaciones en paisajes de gradiente ruidosos.

El segundo momento, como en RMSprop, adapta la tasa de aprendizaje para cada parámetro. Normaliza eficazmente las actualizaciones de los parámetros, ralentizando el aprendizaje para los parámetros con gradientes grandes y acelerándolo para los que tienen gradientes pequeños. Esto permite a Adam manejar con eficacia parámetros a diferentes escalas.

Adam también incorpora corrección de sesgo para estas medias móviles, lo que es especialmente importante en las primeras fases del entrenamiento. Esta corrección ayuda a Adam a empezar con tamaños de paso más precisos, lo que puede conducir a un progreso inicial más rápido.

Combinando estos elementos, Adam consigue a menudo una convergencia más rápida que los métodos de optimización más sencillos. Es especialmente eficaz en problemas con gradientes ruidosos, objetivos no estacionarios o conjuntos de datos muy grandes. La naturaleza adaptativa de Adam lo hace relativamente insensible a la tasa de aprendizaje inicial, por lo que a menudo requiere menos ajuste de hiperparámetros que otros métodos.

Crear una tabla comparativa de optimizadores

Ahora, veamos cómo generar la tabla resumen que vimos antes:

comparison_table

Definimos una función llamada run_optimization para entrenar un modelo de regresión lineal utilizando nuestras funciones de optimización. La función también capturará las puntuaciones de tiempo de ejecución y RMSE:

import time
def run_optimization(opt_func, x, y, **kwargs):
   # Start a timer
   start_time = time.time()
  
   # Run the optimization function
   m, b = opt_func(x, y, **kwargs)
  
   # End the timer
   end_time = time.time()
   # Run the model on the test set with found parameters
   y_preds = model(m, test_xy[:, 0], b)
   y_preds_denormalized = y_preds * std[1] + mean[1]
   y_true_denormalized = test_xy[:, 1] * std[1] + mean[1]
  
   # Compute MSE and RMSE
   actual_mse = np.mean((y_true_denormalized - y_preds_denormalized) ** 2)
   return end_time - start_time, np.sqrt(actual_mse)

Ahora, llamaremos a esta función cuatro veces para cada una de nuestras funciones de optimización, almacenando los resultados en una lista en la que cada elemento es una tripleta (nombre del algoritmo, tiempo de ejecución en segundos, puntuación RMSE):

# Run all optimization methods
results = []
results.append(
   (
       "SGD",
       *run_optimization(
           stochastic_gradient_descent,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.1,
           epochs=10000,
           batch_size=64,
       ),
   )
)
results.append(
   (
       "SGD with Momentum",
       *run_optimization(
           stochastic_gradient_descent_with_momentum,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.1,
           epochs=10000,
           batch_size=64,
           momentum=0.9,
       ),
   )
)
results.append(
   (
       "RMSprop",
       *run_optimization(
           rmsprop_optimization,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.01,
           epochs=10000,
           batch_size=64,
           beta=0.9,
           epsilon=1e-8,
       ),
   )
)
results.append(
   (
       "Adam",
       *run_optimization(
           adam_optimization,
           train_xy[:, 0],
           train_xy[:, 1],
           learning_rate=0.01,
           epochs=10000,
           batch_size=64,
           beta1=0.9,
           beta2=0.999,
           epsilon=1e-8,
       ),
   )
)

Para que la comparación sea justa, mantenemos iguales la tasa de aprendizaje, el número de épocas y el tamaño del lote.

Después, podemos crear nuestra tabla:

from tabulate import tabulate  # pip install tabulate
# Create and print the table
headers = ["Optimization Method", "Runtime (seconds)", "Actual RMSE"]
print(tabulate(results, headers=headers, floatfmt=".4f"))
# Save the table
pd.DataFrame(results, columns=headers).to_csv("optimization_results.csv", index=False)

He aquí el resultado final:

Optimization Method      Runtime (seconds)       Actual RMSE
---------------------  -------------------  ----------------
SGD                                49.9305   1424002054.8658
SGD with Momentum                  50.7744  14239929470.0458
RMSprop                            41.9895    137715232.4602
Adam                                1.8462         1570.1177

Antes de continuar, te animo a que juegues con los parámetros de cada función de optimización. Es probable que puedas hacer que cada uno de ellos, especialmente Adam, sea aún más rápido y preciso ajustando la velocidad de aprendizaje, aumentando el tamaño del lote o controlando el sesgo.

Consulta la sección de conclusiones para ver los enlaces al código completo del script de comparación y cómo crear la trama que hemos visto al principio.

Utilizar Adam en PyTorch

Utilizar a Adam en la práctica no requiere leer un largo artículo como éste y escribirlo tú mismo desde cero. Su implementación en PyTorch está más que a la altura de cualquier tarea de aprendizaje supervisado en aprendizaje profundo.

Aquí tienes un breve fragmento que describe un flujo de trabajo típico de PyTorch que utiliza la herramienta Adam del módulo torch.optim módulo:

# Import necessary modules
import torch
import torch.nn as nn
import torch.optim as optim
# Define your model
model = nn.Sequential(
   nn.Linear(10, 50),
   nn.ReLU(),
   nn.Linear(50, 1)
)
# Initialize Adam optimizer
optimizer = optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
# Training loop
for epoch in range(num_epochs):
   for batch in dataloader:
       # Zero the gradients
       optimizer.zero_grad()
      
       # Forward pass
       outputs = model(batch)
       loss = criterion(outputs, targets)
      
       # Backward pass
       loss.backward()
      
       # Update weights
       optimizer.step()
# Adjusting learning rate
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(num_epochs):
   train(...)
   scheduler.step()

Para saber más sobre el uso de PyTorch en general y sus algoritmos de optimización, consulta este curso introductorio de DataCamp:

• Curso de Introducción al Aprendizaje Profundo en PyTorch | DataCamp

Conclusión

En este artículo, hemos aprendido los entresijos del popular optimizador Adam. En primer lugar, empezamos por construir una intuición sobre él, a través de discusiones sobre sus algoritmos fundacionales, como el descenso de gradiente, el SGD y el RMSprop. Hemos visto cómo Adam combina las ideas principales de éstos, dando como resultado un algoritmo muy flexible y eficaz.

A continuación, cubrimos cómo implementar el Optimizador Adam en Python utilizando sólo NumPy. Al igual que su intuición, hemos construido el código a partir de los algoritmos fundacionales, desde el descenso de gradiente en mini lotes hasta Adam, pasando por el RMSprop. También hemos comprobado una asombrosa diferencia entre Adam y otros algoritmos en cuanto a velocidad y rendimiento creando un sencillo script de evaluación comparativa.

Al final, hemos mostrado cómo utilizar a Adam en PyTorch, tal y como lo harías en la práctica, para resolver problemas de aprendizaje profundo. Aquí tienes algunos enlaces a los scripts que hemos utilizado en el tutorial:

• Aplicación de SGD en mini lotes
• SGD con aplicación de Momentum
• Implementación de RMSprop
• Aplicación de Adán
• Script de evaluación comparativa para comparar los cuatro algoritmos de optimización
• Un script para trazar resultados de pruebas comparativas con Matplotlib

Y algunos recursos relacionados para saber más sobre PyTorch y sus funciones de optimización:

• Tutorial de PyTorch: Construir una red neuronal sencilla desde cero
• Pista de Aprendizaje Profundo en Python
• Curso Intermedio de Aprendizaje Profundo en PyTorch
• Curso de Aprendizaje Profundo para Imágenes con PyTorch

¡Gracias por leer!