Curso
El ANOVA permite comprobar si existen diferencias significativas entre las medias de los grupos, lo que ayuda a los investigadores a determinar si la variación de los datos se debe a diferencias reales entre los grupos o sólo al azar. Este método es beneficioso cuando se trata de experimentos o estudios que implican a más de dos grupos, en los que las pruebas t tradicionales pueden no ser apropiadas o eficientes.
Este artículo explorará los fundamentos de la prueba ANOVA, su finalidad, los dos tipos principales y una guía paso a paso para realizar ANOVA. Comprender estos conceptos puede ayudarte a elegir la prueba correcta para tus datos y a interpretar los resultados con seguridad. También consideraremos un ejemplo para comprender mejor el concepto. Si no conoces la idea de la comprobación de hipótesis en general, lee nuestro artículo Pruebas de hipótesis fáciles tutorial.
¿Qué es una prueba ANOVA?
ANOVA significa Análisis de la Varianza, una prueba estadística utilizada para comparar las medias de tres o más grupos. Analiza la varianza dentro del grupo y entre grupos. El objetivo principal es evaluar si la varianza observada entre las medias de los grupos es más significativa que dentro de los grupos. Si la varianza observada entre las medias de los grupos es significativa, sugiere que las diferencias son significativas.
Matemáticamente, el ANOVA descompone la variabilidad total de los datos en dos componentes:
- Variabilidad dentro del grupo: Variabilidad causada por las diferencias dentro de los grupos individuales, que refleja fluctuaciones aleatorias.
- Variabilidad entre grupos: Variabilidad causada por las diferencias entre las medias de los distintos grupos.

Estadístico F para calcular el ANOVA. Imagen del autor
La prueba produce un estadístico F, que muestra la relación entre la variabilidad entre grupos y la variabilidad dentro de los grupos. Si el estadístico F es suficientemente grande, indica que al menos una de las medias de grupo es significativamente diferente de las demás.
Para entenderlo mejor, considera un escenario en el que se te pide que evalúes el rendimiento de un alumno (notas del examen) basándote en tres métodos de enseñanza: conferencia, taller interactivo y aprendizaje en línea. El ANOVA puede ayudarnos a evaluar si el método de enseñanza influye estadísticamente en el rendimiento del alumno en los exámenes.
Los dos tipos de prueba ANOVA
Hay dos tipos de ANOVA: unidireccional y bidireccional. Dependiendo del número de variables independientes y de cómo interactúen entre sí, ambas se utilizan en distintos escenarios.
1. ANOVA unidireccional
La prueba ANOVA unidireccional se utiliza cuando hay una variable independiente con dos o más grupos. El objetivo es determinar si existe una diferencia significativa entre las medias de los distintos grupos.
En nuestro ejemplo, podemos utilizar el ANOVA de una vía para comparar la eficacia de los tres métodos de enseñanza diferentes (conferencia, taller y aprendizaje en línea) sobre las puntuaciones de los alumnos en los exámenes. El método de enseñanza es la variable independiente con tres grupos, y la nota del examen es la variable dependiente.
- Hipótesis nula (H₀): Las puntuaciones medias de los alumnos en los exámenes de los tres métodos de enseñanza son iguales (no hay diferencia de medias).
- Hipótesis alternativa (H₁): Al menos la media de un grupo difiere significativamente.
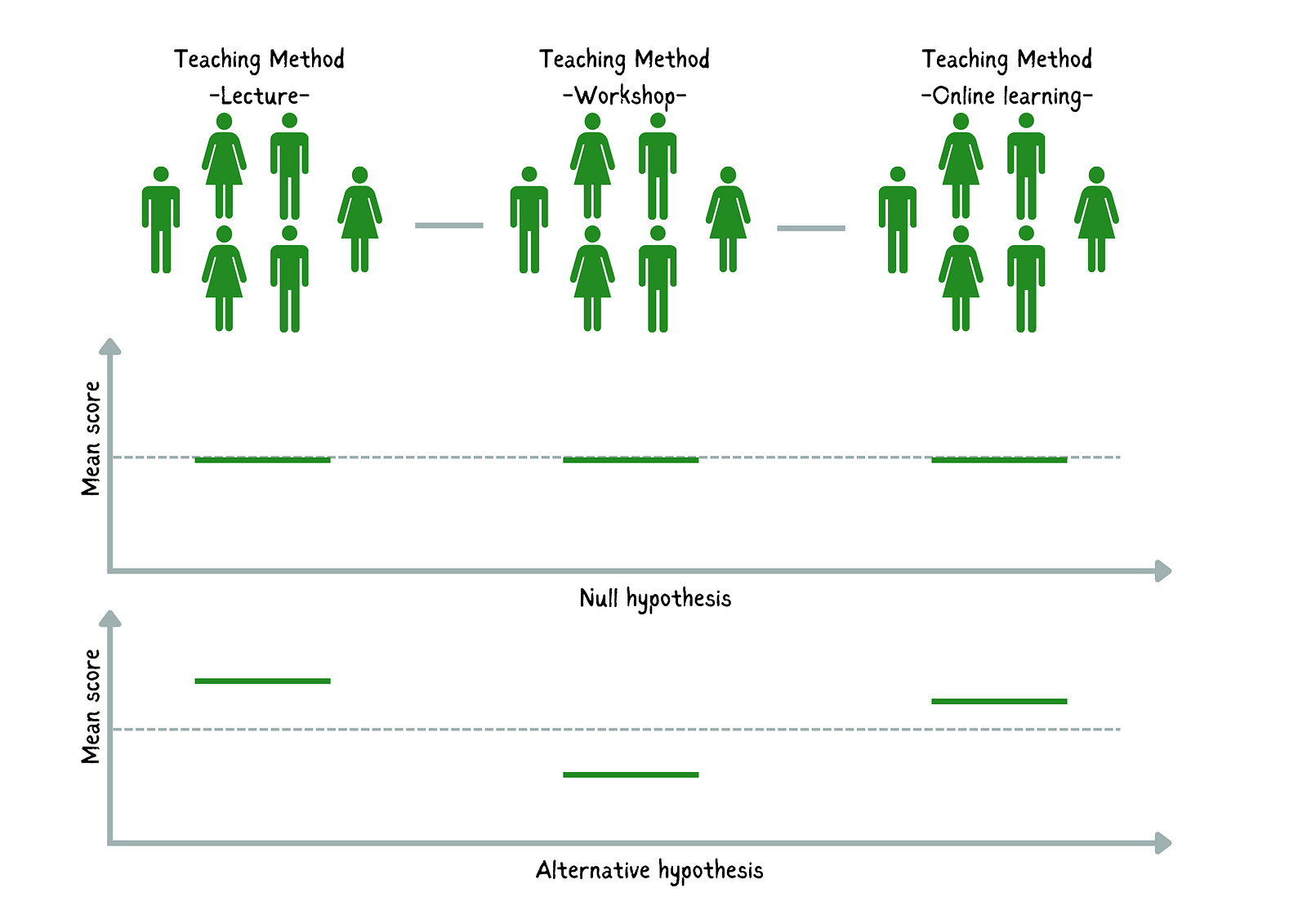 de hipótesis nula Comparación de las hipótesis nula y alternativa. Imagen del autor
de hipótesis nula Comparación de las hipótesis nula y alternativa. Imagen del autor
La prueba ANOVA unidireccional nos dirá si la variación en las puntuaciones de los alumnos en los exámenes puede atribuirse a las diferencias en los métodos de enseñanza o si es probable que se deba al azar.
El ANOVA unidireccional es eficaz cuando se analiza el impacto de un único factor en varios grupos, lo que simplifica su interpretación. Sin embargo, no tiene en cuenta la posibilidad de interacción entre múltiples variables independientes, en cuyo caso se hace necesario un ANOVA de dos vías.
2. ANOVA de dos vías
El ANOVA de dos vías se utiliza cuando hay dos variables independientes, cada una con dos o más grupos. El objetivo es analizar cómo influyen ambas variables independientes en la variable dependiente.
Supongamos que te interesa la relación entre los métodos de enseñanza y las técnicas de estudio y cómo afectan conjuntamente al rendimiento de los alumnos. El ANOVA de dos vías es adecuado para este escenario. Aquí ponemos a prueba tres hipótesis:
- El efecto principal del factor 1 (método de enseñanza): ¿Influye el método de enseñanza en los resultados de los exámenes de los alumnos?
- El efecto principal del factor 2 (técnica de estudio): ¿Afecta la técnica de estudio a las calificaciones de los exámenes?
- Efecto de interacción: ¿Depende la eficacia del método de enseñanza de la técnica de estudio utilizada?
Por ejemplo, un ANOVA de dos vías podría revelar que los alumnos que utilizan el método de clase magistral obtienen mejores resultados en el estudio en grupo, y los que utilizan el aprendizaje online podrían obtener mejores resultados en el estudio individual. Comprender estas interacciones proporciona una visión más profunda de cómo los distintos factores juntos influyen en los resultados.
ANOVA vs. Prueba T
Te estarás preguntando: ¿Cuándo debo elegir un ANOVA en lugar de una prueba t? La prueba t y el ANOVA se utilizan para comparar medias entre grupos, pero la elección entre ellos depende del número de grupos que se comparen y de la complejidad de la estructura de datos.
Cuándo utilizar una prueba T
Una prueba t es adecuada cuando se comparan las medias de dos grupos. Por ejemplo, si quisiéramos comparar las puntuaciones en los exámenes de los alumnos que utilizan sólo dos métodos de enseñanza -clase magistral y taller-, bastaría con una prueba t. Hay dos tipos de pruebas t:
- Prueba T independiente: Compara dos grupos independientes (por ejemplo, conferencia frente a taller).
- Prueba T pareada: Compara las medias de un mismo grupo en distintos momentos (por ejemplo, el rendimiento de los alumnos antes y después de utilizar un método de enseñanza concreto).
Cuándo utilizar el ANOVA
En cambio, el ANOVA se utiliza cuando se comparan las medias de tres o más grupos. Nuestro estudio incluye tres métodos de enseñanza (conferencia, taller y aprendizaje en línea), por lo que se requiere algo más que una prueba t. Utilizar múltiples pruebas t para cada par de grupos aumentaría el riesgo de error de tipo I (falsos positivos), mientras que el ANOVA maneja la comparación en una sola prueba y controla este error.
Supuestos de la prueba ANOVA
Todas las pruebas estadísticas tienen supuestos que deben cumplirse para garantizar la validez de los resultados.
He aquí los supuestos que deben cumplirse para el ANOVA:
1. Independencia de las observaciones
Las observaciones (puntos de datos) deben ser independientes entre sí. En el ejemplo, las puntuaciones de los alumnos en los exámenes de un método de enseñanza no deben influir en las puntuaciones de los alumnos de otro método.
2. Homogeneidad de varianzas
Las varianzas dentro de cada grupo deben ser aproximadamente iguales. El ANOVA supone que la variabilidad de las puntuaciones de los exámenes dentro de cada grupo de métodos de enseñanza es aproximadamente la misma. Esto puede comprobarse mediante la prueba de Levene, que comprueba la igualdad de varianzas.
3. Distribución normal
Los datos de cada grupo deben seguir una distribución normal. En nuestro ejemplo de método de enseñanza, lo ideal es que las puntuaciones de los exámenes de los alumnos de cada grupo de enseñanza (Clase, Taller, Aprendizaje online) se distribuyan normalmente.
Si se incumple algún supuesto, los resultados de la prueba pueden no ser válidos. En estos casos, es esencial plantearse utilizar una prueba no paramétrica.
Realizar una prueba ANOVA
Utilizaremos el mismo ejemplo de comparar distintos métodos de enseñanza para examinar cómo afectan a las puntuaciones de los alumnos en los exámenes. Supongamos que te proporcionan los siguientes datos que muestran las puntuaciones de los exámenes (variable dependiente) en función del método de enseñanza (variable independiente).
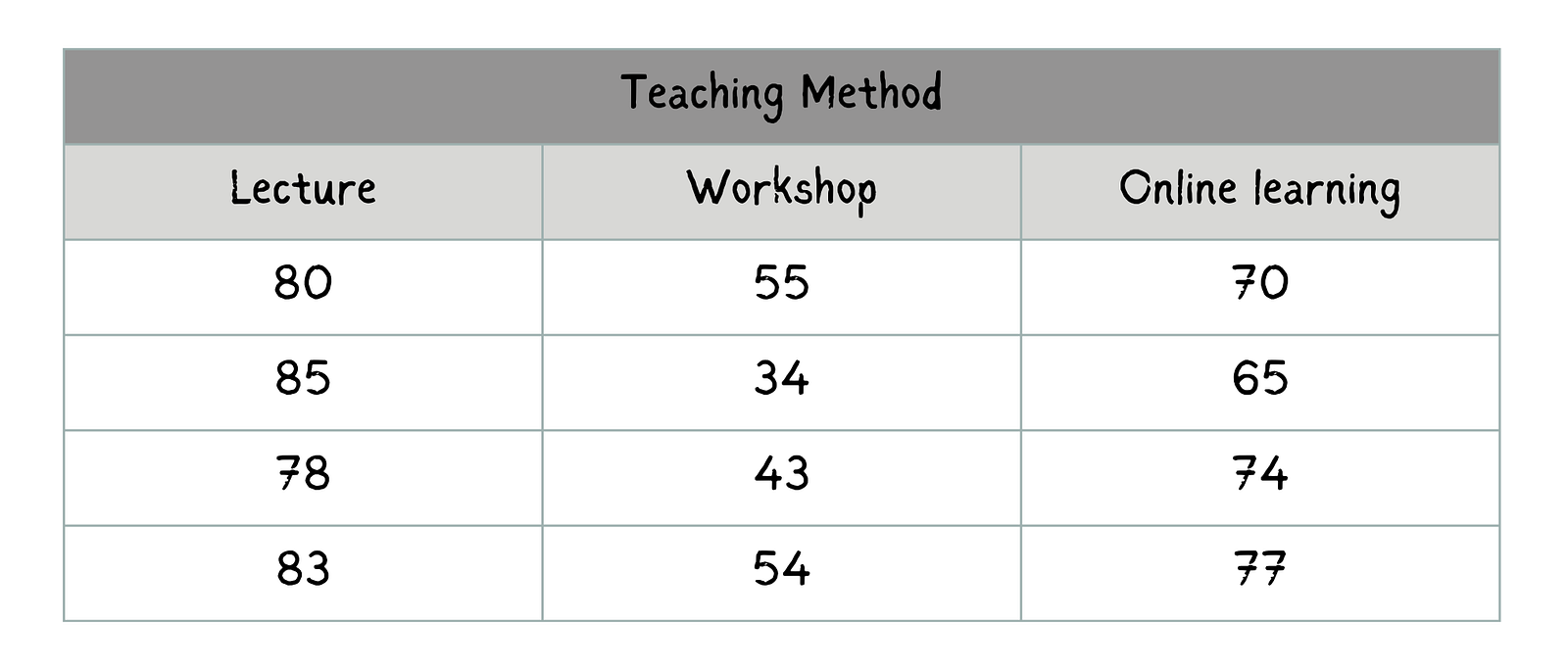 de los exámenes de cada método de enseñanza de cuatro alumnos cada unoPuntuaciones de los exámenes de cada método de enseñanza de cuatro alumnos cada uno. Imagen del autor
de los exámenes de cada método de enseñanza de cuatro alumnos cada unoPuntuaciones de los exámenes de cada método de enseñanza de cuatro alumnos cada uno. Imagen del autor
Paso 1: Define la hipótesis
El primer paso del proceso es definir la hipótesis. Enuncia las hipótesis nula y alternativa:
- Hipótesis nula (H₀): Las medias de las puntuaciones de los exámenes de los alumnos de los tres métodos de enseñanza son iguales.
- Hipótesis alternativa (H₁): Al menos un método de enseñanza tiene una puntuación media diferente en el examen.
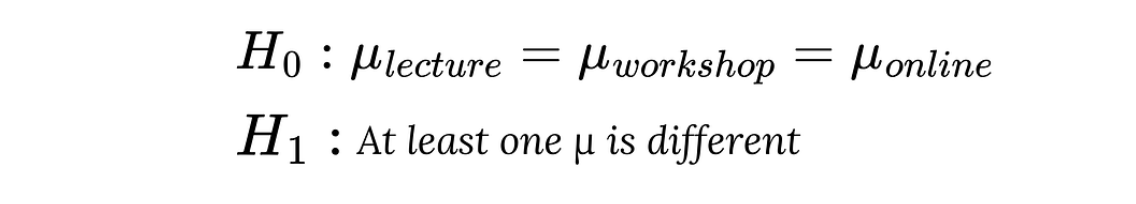
Hipótesis nula e hipótesis alternativa. Imagen del autor
Paso 2: Comprueba los supuestos del ANOVA
Antes de realizar el ANOVA, asegúrate de que se cumplen los supuestos. Normalidad, independencia y homogeneidad de varianzas. Para simplificar, vamos a suponer que se cumplen todos los supuestos.
Paso 3: Calcular ANOVA
Una vez comprobados los supuestos, calcula el ANOVA.
La fórmula del estadístico F en el ANOVA unidireccional se define a continuación.

Estadístico F en ANOVA unidireccional. Imagen del autor
El estadístico F en el ANOVA unidireccional es la relación entre la suma cuadrática media entre los grupos y la suma cuadrática media dentro de los grupos.
Para llegar a esto, vayamos paso a paso.
1. Calcula la media de cada grupo y la media global.
Utiliza la ecuación siguiente para calcular la media de cada método de enseñanza (Ai). Divide la suma de las puntuaciones de los exámenes de cada grupo por el número de alumnos de cada grupo.
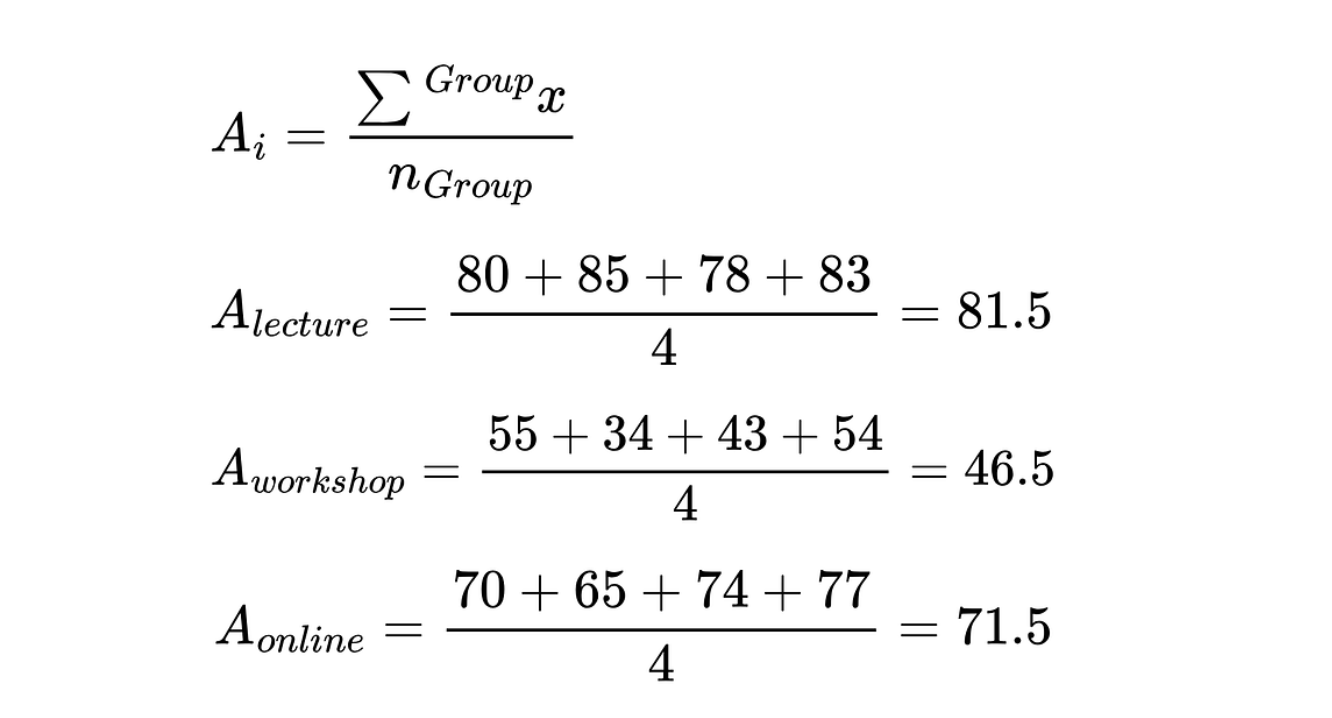
Media de cada grupo (método de enseñanza). Imagen del autor
A continuación, calcula la media global (G) dividiendo la suma de todas las instancias por el número total de alumnos.
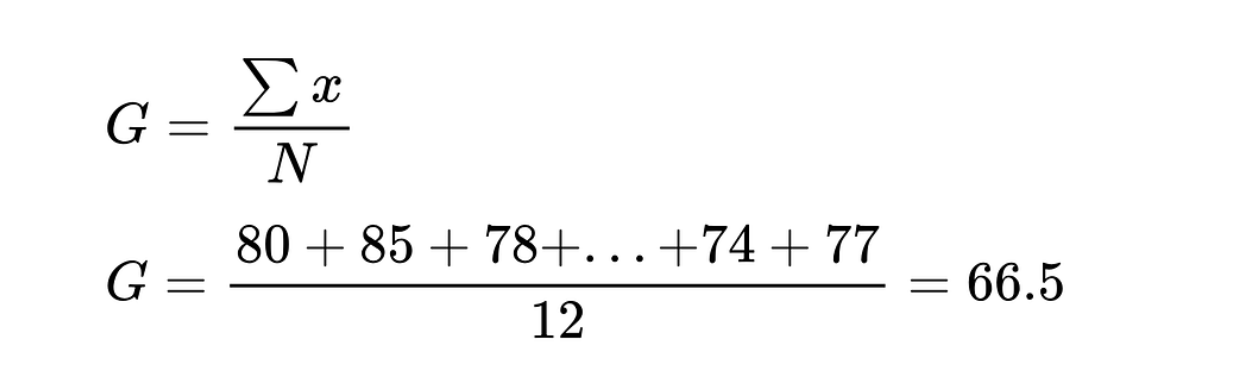
Media global de las puntuaciones de los exámenes. Imagen del autor
2. Calcula la suma de cuadrados de cada grupo
La ecuación es la siguiente para calcular la suma de cuadrados de cada grupo.
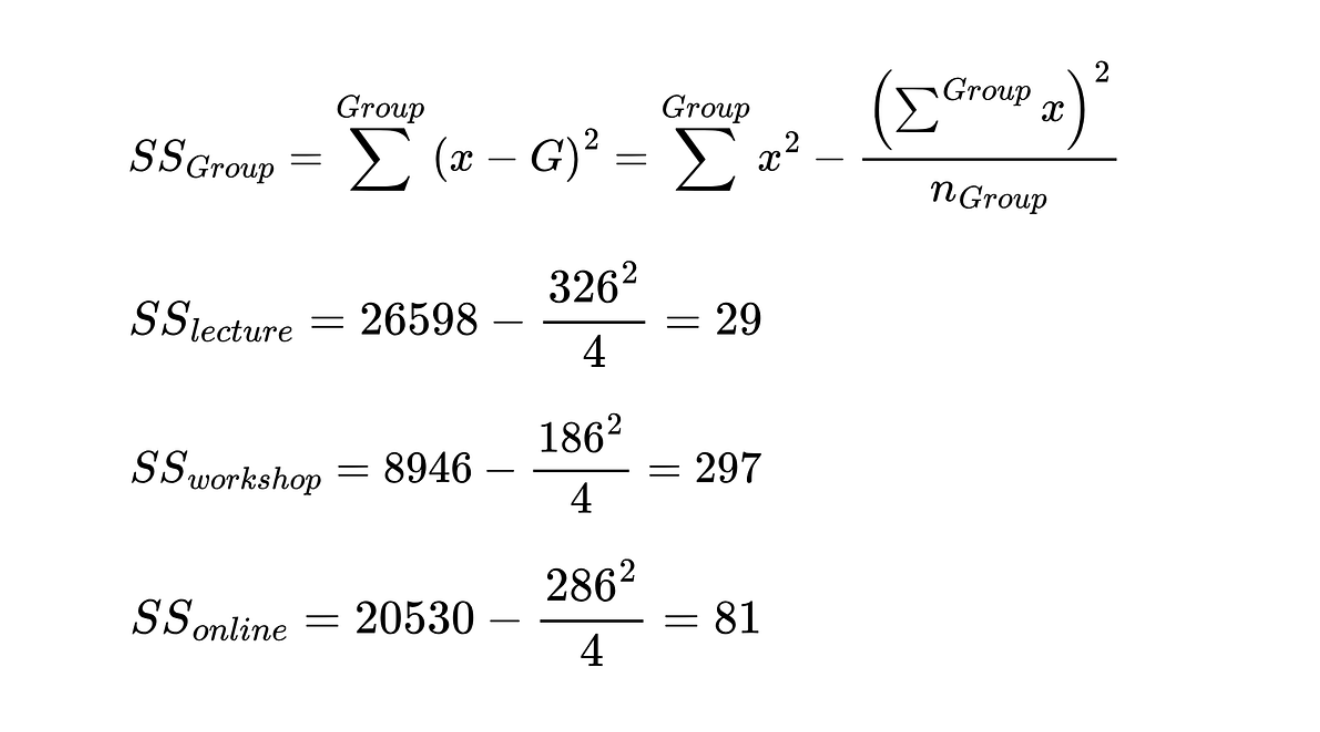
La suma de cuadrados para cada método de enseñanza. Imagen del autor
Después de calcular, rellena esta tabla con los valores para facilitar el acceso.
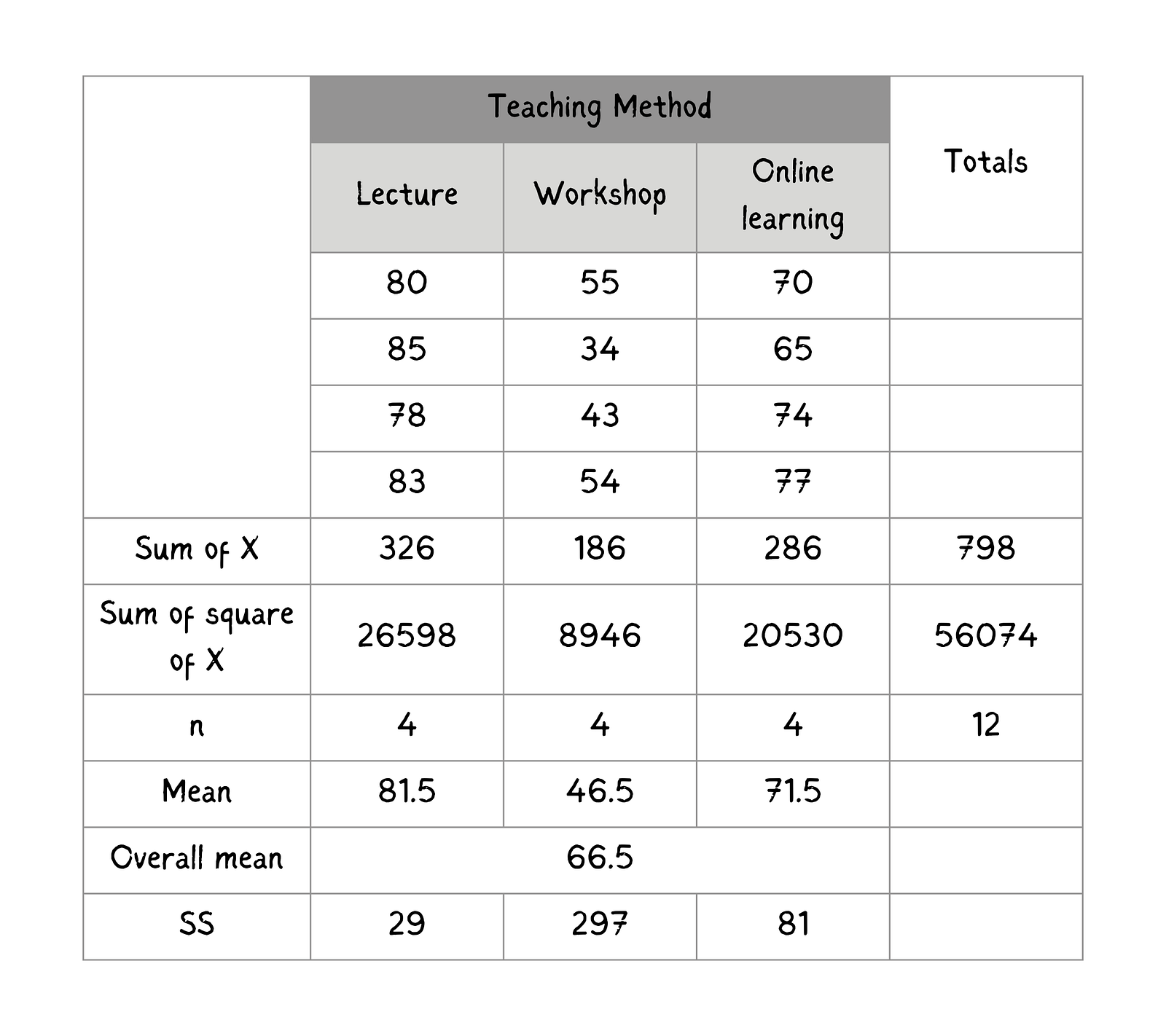 Resumen del rendimiento de los alumnos por método de enseñanza. Imagen del autor
Resumen del rendimiento de los alumnos por método de enseñanza. Imagen del autor
3. Calcula la suma de cuadrados entre el grupo, la suma de cuadrados dentro del grupo y la suma total de cuadrados.
Utilizando la ecuación siguiente, calcula la suma de cuadrados entre los grupos. En la ecuación,
- Ai: Media del grupo
- G: Media global
- ni: número de instancias en cada grupo
Utiliza los valores de la tabla resumen para el cálculo.
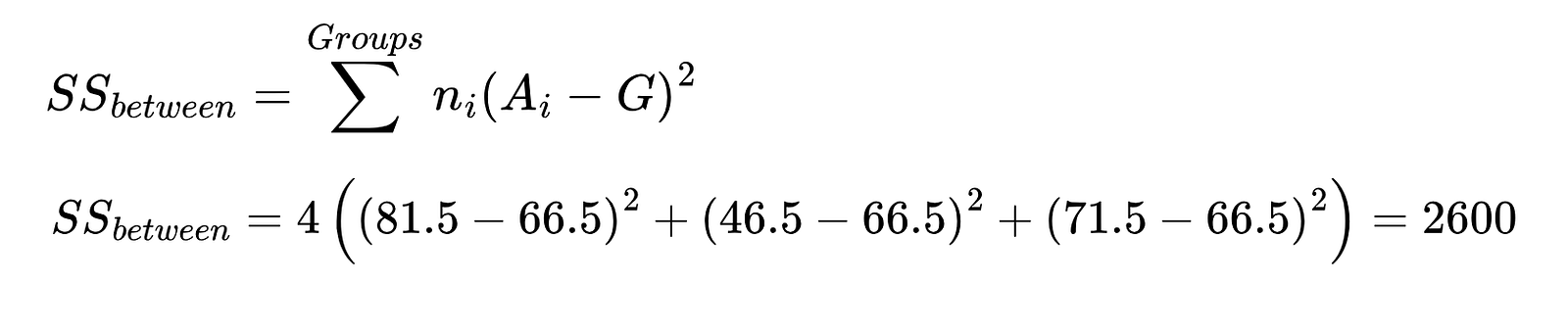 Suma de cuadrados entre el grupo
Suma de cuadrados entre el grupo
A continuación, calcula la suma de cuadrados dentro del grupo. Es la suma de la suma de cuadrados (SS) de cada grupo.
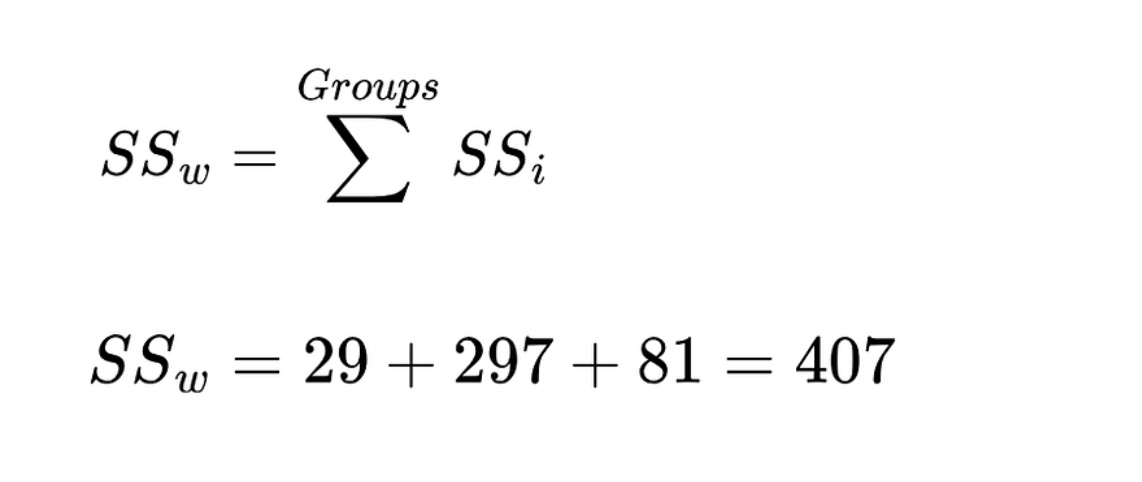
Suma de cuadrados dentro del grupo. Imagen del autor
Utiliza la ecuación siguiente para calcular la suma total de cuadrados 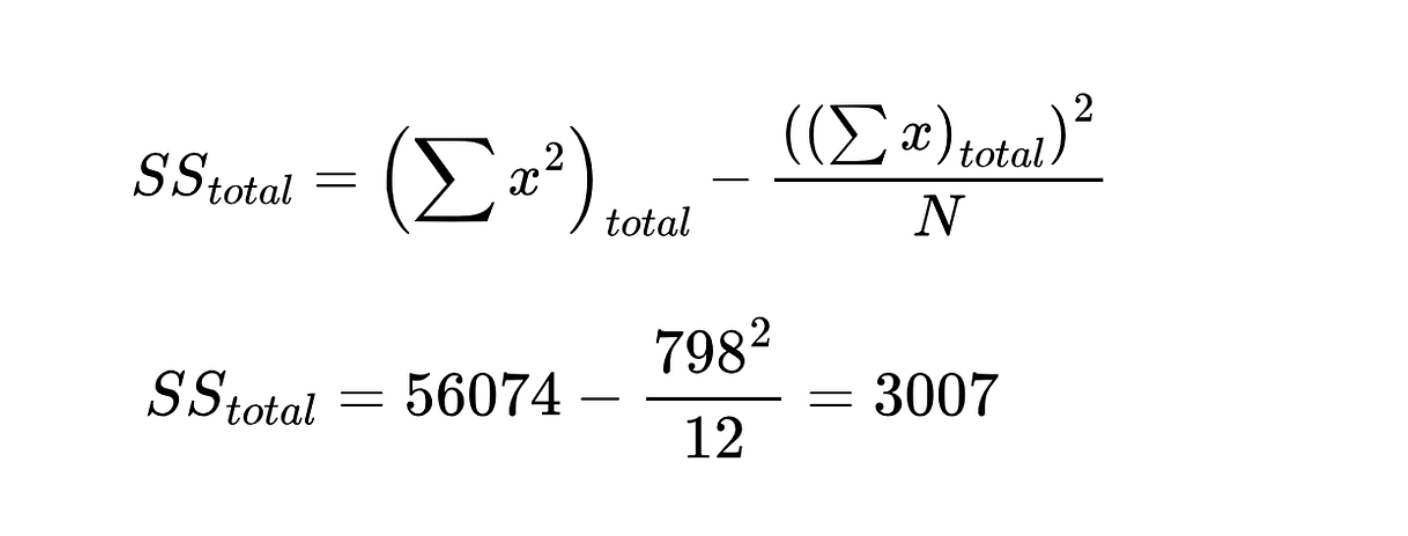 Suma total de cuadrados. Imagen del autor
Suma total de cuadrados. Imagen del autor
Verifica el cálculo comprobando si la suma total de cuadrados es la suma de la suma de cuadrados entre los grupos y la suma de cuadrados dentro del grupo. Tras comprobarlo, pasa a calcular los cuadrados medios.
4. Calcula los cuadrados medios
Los cuadrados medios son la relación entre las sumas cuadradas y el grado de libertad.
El grado de libertad entre grupos df_between es igual al número de grupos menos uno, y el grado de libertad dentro de los grupos df_w es igual al número total de participantes menos el número de grupos.
Con los valores calculados en el paso anterior, calcula los cuadrados medios.
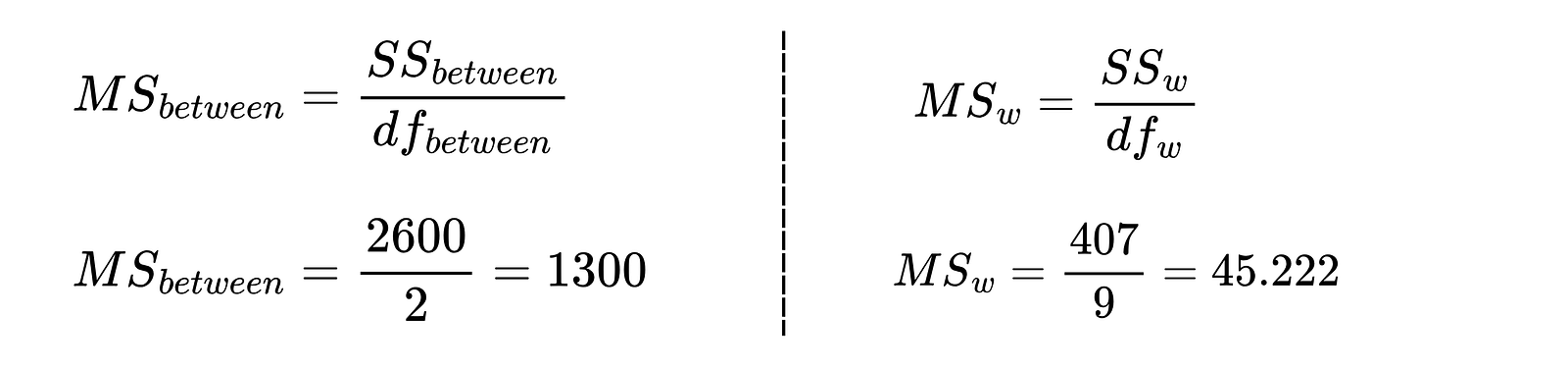 Cuadrados medios entre los grupos y dentro de los Cuadrados medios entre los grupos y dentro de los grupos. Imagen del autor
Cuadrados medios entre los grupos y dentro de los Cuadrados medios entre los grupos y dentro de los grupos. Imagen del autor
5. Calcula el estadístico F utilizando la siguiente ecuación
El estadístico F es la relación entre el cuadrado medio entre el grupo y el cuadrado medio dentro del grupo.
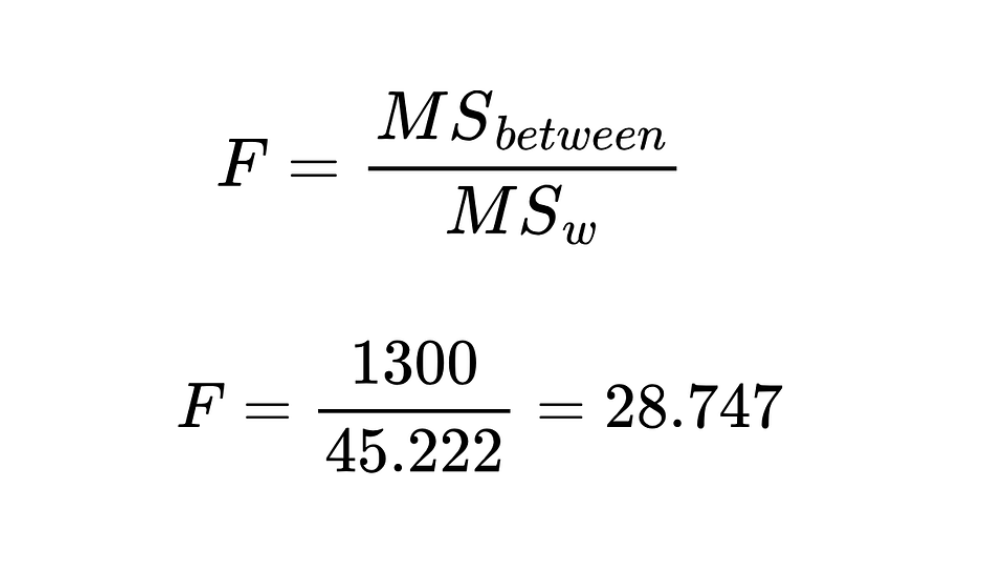
Estadístico F. Imagen del autor
El valor calculado del estadístico F es 28,747.
Por último, el valor p se calcula utilizando el estadístico F, el grado de libertad df, y la tabla de distribución F.
En este ejemplo, el numerador df es 2, el denominador df es 9 y el estadístico F es 28,747. Por tanto, el valor p de la tabla de distribución F es 0,000123.
Paso 4: Interpreta los resultados
- Estadística F: El estadístico F mide la relación entre la variación entre grupos y la variación dentro de los grupos. Un estadístico F más alto indica una diferencia más significativa entre las medias de los grupos en relación con la variación aleatoria.
- Valor P: El valor p determina si las diferencias entre las medias de los grupos son estadísticamente significativas. Si el valor p está por debajo de un umbral predefinido (normalmente 0,05), rechaza la hipótesis nula y concluye que al menos un grupo tiene una media significativamente diferente.
El valor p es 0,000123, y rechazaríamos la hipótesis nula para concluir que el método de enseñanza afecta significativamente a las calificaciones de los exámenes.
Pruebas post hoc tras ANOVA
El ANOVA nos dice si hay una diferencia estadísticamente significativa entre las medias de los grupos, pero no especifica qué grupos son significativamente diferentes entre sí. Éste es el papel de las pruebas post-hoc: realizan comparaciones por pares entre los grupos para identificar con precisión dónde existen las diferencias. Cuando tienes más de dos grupos, estas pruebas son esenciales, y el resultado del ANOVA es significativo.
Siguiendo con nuestro ejemplo, la prueba revela una diferencia significativa en las puntuaciones de los alumnos en los exámenes tras realizar el ANOVA unidireccional sobre los tres métodos de enseñanza (Clase teórica, Taller y Aprendizaje en línea). Una prueba post hoc nos ayudará a determinar qué métodos de enseñanza influyen de forma diferente en el rendimiento en los exámenes.
La Diferencia Honestamente Significativa (HSD) de Tukey y la Corrección de Bonferroni son pruebas post hoc muy utilizadas.
Alternativas al ANOVA
Si no se cumplen los supuestos del ANOVA, o cuando el ANOVA no es adecuado para el conjunto de datos, considera las siguientes alternativas.
- Prueba de Kruskal-Wallis: Es una alternativa no paramétrica al ANOVA unidireccional cuando se incumple el supuesto de normalidad. Es una versión ampliada de la prueba U de Mann-Whitney.
- MANOVA (Análisis Multivariante de la Varianza): Amplía los principios del ANOVA a múltiples variables dependientes. Comprueba si los vectores medios de múltiples variables dependientes difieren entre grupos.
Conclusión
Este artículo introduce los conceptos básicos del ANOVA y destaca cuándo utilizarlo frente a una prueba t. Aprendimos que el ANOVA es un análisis estadístico robusto que compara varios grupos simultáneamente. Proporcionamos una guía paso a paso para realizar el ANOVA, detallando cómo formular hipótesis, comprobar los supuestos e interpretar los resultados.
Para obtener experiencia práctica en el uso de ANOVA en Excel, consulta el tutorial Guía completa para el uso de ANOVA en Excel. Considera la posibilidad de realizar los cursos Fundamentos de la Inferencia en Python y Estadística Inferencial para ampliar tus conocimientos de estadística.

Como científico de datos senior, diseño, desarrollo e implanto soluciones de aprendizaje automático a gran escala para ayudar a las empresas a tomar mejores decisiones basadas en datos. Como escritora de ciencia de datos, comparto aprendizajes, consejos profesionales y tutoriales prácticos en profundidad.
Preguntas frecuentes
¿Qué es el ANOVA y por qué se utiliza?
ANOVA, o Análisis de la Varianza, es una prueba estadística que compara las medias de tres o más grupos. Ayuda a determinar si las diferencias observadas entre los grupos son significativas o se deben al azar.
¿Cuál es la diferencia entre ANOVA unidireccional y bidireccional?
El ANOVA de una vía compara las medias de los grupos basándose en una variable independiente. El ANOVA de dos vías examina el impacto de dos variables independientes y su interacción.
¿Cuándo debo utilizar el ANOVA en lugar de una prueba t?
Utiliza el ANOVA cuando compares las medias de tres o más grupos. Una prueba t es adecuada para comparar las medias de dos grupos.
¿Cuáles son los supuestos clave para realizar un ANOVA?
El ANOVA requiere independencia de las observaciones, homogeneidad de las varianzas (varianzas iguales en todos los grupos) y una distribución normal de los datos dentro de cada grupo.
¿Qué indica un estadístico F significativo en ANOVA?
Un estadístico F significativo significa que al menos la media de un grupo es significativamente diferente, lo que indica que las diferencias entre los grupos no se deben al azar.