Pruebas de hipótesis fáciles

La comprobación de hipótesis es una parte clave de la estadística que te ayuda a tomar decisiones informadas en una amplia gama de campos, desde la medicina a la economía, pasando por las ciencias sociales. Esta guía te guiará a través de los conceptos básicos, los tipos, los pasos y las aplicaciones reales de las pruebas de hipótesis, garantizando que puedas interpretar y presentar con confianza tus resultados estadísticos.

Si estás preparado para aprender más sobre la comprobación de hipótesis, selecciona el curso que se ajuste a tu tecnología preferida: Pruebas deHipótesis en Python, Pruebas de Hipótesis en R o Introducción a la Estadística en Google Sheets. También puedes seguir nuestro curso de Introducción a la Estadística, que es independiente de la tecnología.

¿Qué es la comprobación de hipótesis?

La comprobación de hipótesis es un procedimiento estadístico utilizado para comprobar supuestos o hipótesis sobre un parámetro de la población. Implica formular una hipótesis nula (H0) y una hipótesis alternativa (Ha), recopilar datos y determinar si las pruebas son lo suficientemente sólidas como para rechazar la hipótesis nula.

El objetivo principal de la comprobación de hipótesis es hacer inferencias sobre una población a partir de una muestra de datos. Permite a los investigadores y analistas cuantificar la probabilidad de que las diferencias o relaciones observadas en los datos se hayan producido por casualidad en lugar de reflejar un efecto verdadero en la población.

Pasos de la comprobación de hipótesis

Vamos a ver cómo hacer una prueba de hipótesis, paso a paso.

Paso 1: Plantea tus hipótesis

El primer paso es formular tu pregunta de investigación en dos hipótesis contrapuestas:

1. Hipótesis nula (H0): Esta es la suposición por defecto de que no hay ningún efecto o diferencia.
2. Hipótesis alternativa (Ha): Es la hipótesis de que existe un efecto o diferencia.

Por ejemplo:

• H0: La estatura media de los hombres es igual a la estatura media de las mujeres.
• Ha: La estatura media de los hombres no es igual a la estatura media de las mujeres.

Paso 2: Recoger y preparar los datos

Recopila datos mediante experimentos, encuestas o estudios observacionales. Asegúrate de que el método de recogida de datos está diseñado para comprobar la hipótesis y es representativo de la población. Este paso suele implicar:

• Definir la población de interés.
• Seleccionar un método de muestreo adecuado.
• Determinar el tamaño de la muestra.
• Recoger y organizar los datos.

Paso 3: Elige la prueba estadística adecuada

Selecciona una prueba estadística en función del tipo de datos y de la hipótesis. La elección depende de factores como

• Tipo de datos (continuos, categóricos, etc.)
• Distribución de los datos (normal, no normal)
• Tamaño de la muestra
• Número de grupos comparados

Las pruebas más comunes son:

• Pruebas t (para comparar medias)

• pruebas chi-cuadrado (para datos categóricos)

• ANOVA (para comparar medias de varios grupos)

Paso 4: Calcula el estadístico de la prueba y el valor p

Utiliza programas estadísticos o fórmulas para calcular el estadístico de prueba y el valor p correspondiente. Este paso cuantifica cuánto se desvían los datos de la muestra de la hipótesis nula.

El valor p es un concepto importante en la comprobación de hipótesis. Representa la probabilidad de observar resultados tan extremos como los datos de la muestra, suponiendo que la hipótesis nula sea cierta.

Paso 5: Toma una decisión

Compara el valor p con el nivel de significación predeterminado (α), que suele fijarse en 0,05. La regla de decisión es la siguiente

• Si el valor p ≤ α: Rechaza la hipótesis nula, sugiriendo que las pruebas apoyan la hipótesis alternativa.
• Si el valor p > α: No rechazar la hipótesis nula, lo que sugiere que no hay pruebas suficientes para apoyar la hipótesis alternativa.

Es importante señalar que no rechazar la hipótesis nula no prueba que sea cierta; simplemente significa que no hay pruebas suficientes para concluir lo contrario.

Paso 6: Presenta tus conclusiones

Informa de los resultados, incluyendo el estadístico de la prueba, el valor p y la conclusión. Discute si los resultados apoyan la hipótesis inicial y sus implicaciones. Al presentar los resultados, ten en cuenta:

• Proporcionar el contexto para el estudio.
• Establecer claramente las hipótesis.
• Informar del estadístico de la prueba y del valor p.
• Interpretar los resultados en lenguaje sencillo.
• Discutir la importancia práctica de los resultados.

Tipos de pruebas de hipótesis

Las pruebas de hipótesis pueden clasificarse a grandes rasgos en dos tipos principales:

Pruebas paramétricas

Las pruebas paramétricas suponen que los datos siguen una distribución de probabilidad específica, normalmente la distribución normal. Estas pruebas suelen ser más potentes cuando se cumplen los supuestos. Las pruebas paramétricas más comunes son:

• Pruebas t (una muestra, muestras independientes, muestras pareadas)
• ANOVA (unidireccional, bidireccional, medidas repetidas)
• Pruebas Z (una muestra, dos muestras)
• Pruebas F (unidireccional, bidireccional)

Pruebas no paramétricas

Las pruebas no paramétricas no suponen una distribución específica de los datos. Son útiles cuando se trata de datos ordinales o cuando se violan los supuestos de las pruebas paramétricas. Algunos ejemplos son:

• Prueba U de Mann-Whitney
• Prueba de rango con signo de Wilcoxon
• Kruskal-Wallis test

Seleccionar la prueba adecuada

Al elegir una prueba de hipótesis, los investigadores tienen en cuenta algunas categorías generales:

1. Distribución de datos: Determina si tus datos se distribuyen normalmente, ya que muchas pruebas presuponen la normalidad.
2. Número de Grupos: Identifica cuántos grupos estás comparando (por ejemplo, un grupo, dos grupos o más).
3. Independencia del grupo: Decide si tus grupos son independientes (sujetos diferentes) o dependientes (los mismos sujetos medidos varias veces).
4. Tipo de datos:
• Continuo (por ejemplo, altura, peso),
• Ordinal (por ejemplo, clasificaciones),
• Nominal (por ejemplo, categorías sin orden).

En función de estas categorías, puedes seleccionar la prueba estadística adecuada. Por ejemplo, si tus datos se distribuyen normalmente y tienes dos grupos independientes con datos continuos, utilizarías una prueba t independiente. Si tus datos no se distribuyen normalmente con dos grupos independientes y datos ordinales, se recomienda una prueba U de Mann-Whitney.

Para ayudarte a elegir la prueba adecuada, considera la posibilidad de utilizar un diagrama de flujo de pruebas de hipótesis como guía general:

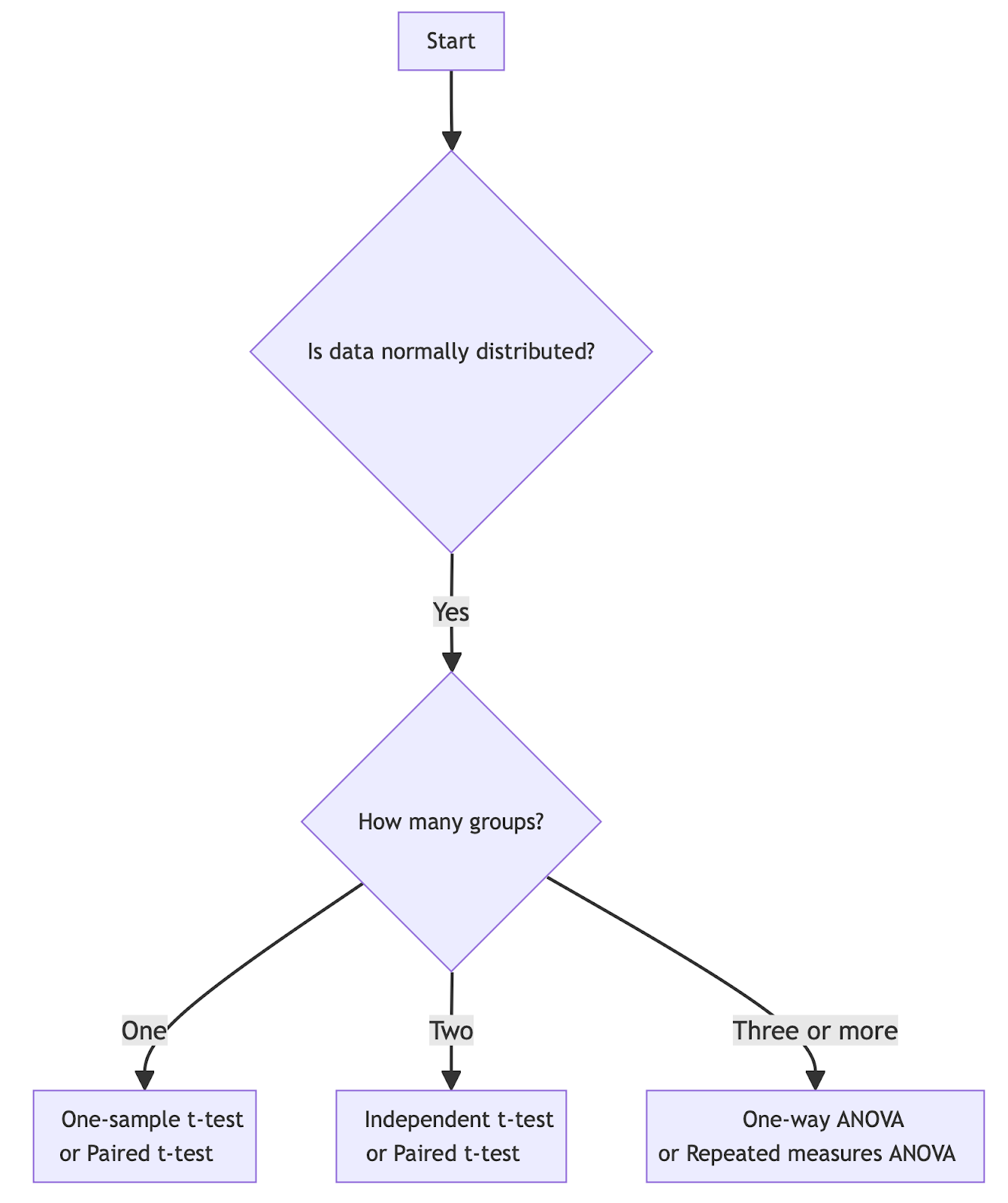
Elegir la prueba de hipótesis adecuada para datos con distribución normal. Imagen del autor.

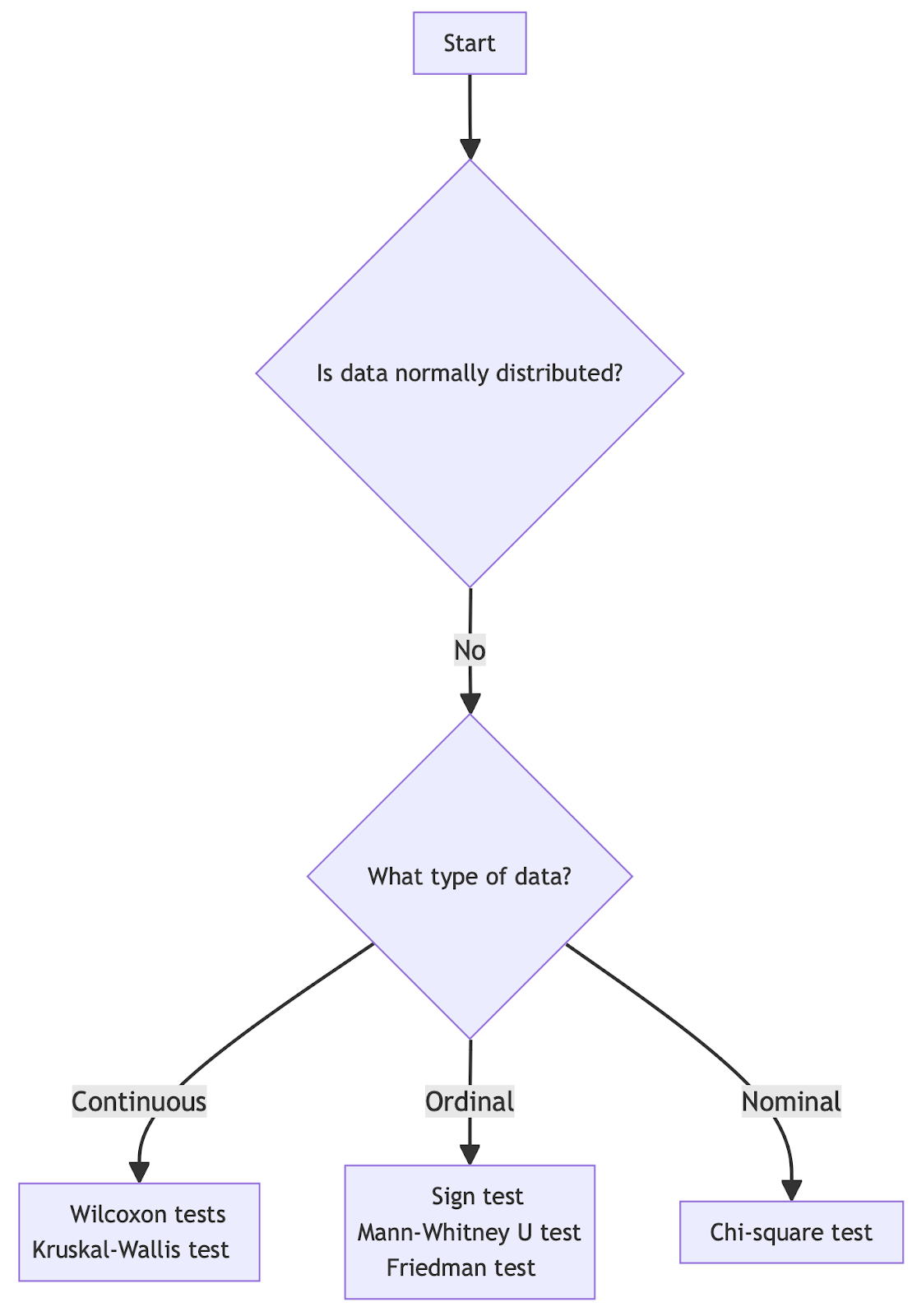
Elegir la prueba de hipótesis adecuada para datos con distribución no normal. Imagen del autor.

Enfoques modernos de la comprobación de hipótesis

Además de los métodos tradicionales de comprobación de hipótesis, existen varios enfoques modernos:

Pruebas de permutación o aleatorización

Estas pruebas implican barajar aleatoriamente los datos observados muchas veces para crear una distribución de posibles resultados bajo la hipótesis nula. Son especialmente útiles cuando se trata de muestras de pequeño tamaño o cuando no se cumplen los supuestos de las pruebas paramétricas.

Bootstrapping

El bootstrapping es una técnica de remuestreo que consiste en realizar repetidamente un muestreo con sustitución a partir del conjunto de datos original. Puede utilizarse para estimar la distribución muestral de una estadística y construir intervalos de confianza.

Simulación Monte Carlo

Los métodos de Montecarlo utilizan el muestreo aleatorio repetido para obtener resultados numéricos. En las pruebas de hipótesis, pueden utilizarse para estimar los valores p de modelos estadísticos complejos o cuando es difícil obtener soluciones analíticas.

Control de errores

Al realizar pruebas de hipótesis, lo mejor es comprender y controlar los posibles errores:

Errores de tipo I y de tipo II

• Error de tipo I: Rechazar la hipótesis nula cuando en realidad es cierta (falso positivo).
• Error de tipo II: No rechazar la hipótesis nula cuando en realidad es falsa (falso negativo).

El nivel de significación (α) controla directamente la probabilidad de un error de tipo I. Disminuir α reduce la probabilidad de errores de tipo I, pero aumenta el riesgo de errores de tipo II.

Para equilibrar estos errores:

1. Ajusta el nivel de significación en función de las consecuencias de cada tipo de error.
2. Aumenta el tamaño de la muestra para mejorar la potencia de la prueba.
3. Utiliza pruebas de una cola cuando proceda.

El efecto cajón archivador

El efecto cajón de sastre se refiere al sesgo de publicación por el que los estudios con resultados significativos tienen más probabilidades de ser publicados que los que tienen resultados no significativos. Esto puede llevar a una sobreestimación de los efectos en la literatura. Para mitigarlo:

• Considera la posibilidad de preinscribir estudios.
• Publica todos los resultados, sean significativos o no.
• Realiza metaanálisis que tengan en cuenta el sesgo de publicación.
• Simula previamente los datos.

Glosario de términos y definiciones clave

• Hipótesis nula (H0): La suposición por defecto de que no hay ningún efecto o diferencia.
• Hipótesis alternativa (Ha): La hipótesis de que existe un efecto o una diferencia.
• Valor P: La probabilidad de observar los resultados de la prueba según la hipótesis nula.
• Nivel de significación (α): El umbral para rechazar la hipótesis nula, comúnmente fijado en 0,05.
• Estadística de prueba: Valor normalizado utilizado para comparar los datos observados con la hipótesis nula.
• Error de tipo I: Rechazar una hipótesis nula verdadera (falso positivo).
• Error de tipo II: No rechazar una hipótesis nula falsa (falso negativo).
• Potencia estadística: La probabilidad de rechazar correctamente una hipótesis nula falsa.
• Intervalo de confianza: Un intervalo de valores que probablemente contenga el verdadero parámetro poblacional.
• Tamaño del efecto: Una medida de la magnitud de la diferencia o relación que se está probando.

Conclusión

Recuerda que la comprobación de hipótesis es sólo una parte del conjunto de herramientas de la inferencia estadística. Considera siempre la importancia práctica de tus conclusiones, no sólo la importancia estadística. A medida que adquieras experiencia, desarrollarás una comprensión de cuándo y cómo aplicar estas técnicas en diversos escenarios del mundo real.

Para mejorar aún más tus conocimientos estadísticos, puedes explorar temas como Cómo ser estadístico en 2024, que ofrece una visión de este campo en evolución y de las habilidades necesarias para tener éxito. Además, practicar las 35 mejores preguntas y respuestas de entrevistas de estadística para 2024 y trabajar con nuestro curso Practicar preguntas de entrevistas de estadística en R puede ayudarte a perfeccionar tus habilidades y prepararte para las entrevistas.