ANOVA-Test: Ein detaillierter Leitfaden mit Beispielen

Mit der ANOVA kannst du testen, ob es signifikante Unterschiede zwischen den Mittelwerten der Gruppen gibt. So kannst du feststellen, ob die Unterschiede in den Daten auf tatsächliche Unterschiede zwischen den Gruppen oder nur auf Zufall zurückzuführen sind. Diese Methode ist vorteilhaft, wenn es um Experimente oder Studien mit mehr als zwei Gruppen geht, bei denen herkömmliche t-Tests möglicherweise nicht angemessen oder effizient sind.

In diesem Artikel geht es um die Grundlagen des ANOVA-Tests, seinen Zweck, die beiden Haupttypen und eine Schritt-für-Schritt-Anleitung zur Durchführung der ANOVA. Das Verständnis dieser Konzepte kann dir helfen, den richtigen Test für deine Daten auszuwählen und die Ergebnisse sicher zu interpretieren. Wir werden auch ein Beispiel betrachten, um das Konzept besser zu verstehen. Wenn du mit der Idee der Hypothesenprüfung im Allgemeinen noch nicht vertraut bist, lies unsere Hypothesentest leicht gemacht Tutorium.

Was ist ein ANOVA-Test?

ANOVA steht für Varianzanalyse, ein statistischer Test, mit dem die Mittelwerte von drei oder mehr Gruppen verglichen werden können. Sie analysiert die Varianz innerhalb der Gruppe und zwischen den Gruppen. Das Hauptziel ist es, festzustellen, ob die beobachtete Varianz zwischen den Gruppenmittelwerten signifikanter ist als innerhalb der Gruppen. Wenn die beobachtete Varianz zwischen den Gruppenmitteln signifikant ist, deutet dies darauf hin, dass die Unterschiede bedeutsam sind.

Mathematisch gesehen zerlegt die ANOVA die Gesamtvariabilität der Daten in zwei Komponenten:

• Variabilität innerhalb der Gruppe: Variabilität, die durch Unterschiede innerhalb einzelner Gruppen verursacht wird und zufällige Schwankungen widerspiegelt.
• Variabilität zwischen den Gruppen: Variabilität, die durch Unterschiede zwischen den Mittelwerten der verschiedenen Gruppen verursacht wird.

F-Statistik zur Berechnung der ANOVA. Bild vom Autor

Der Test ergibt eine F-Statistik, die das Verhältnis zwischen der Variabilität zwischen den Gruppen und der Variabilität innerhalb der Gruppen angibt. Wenn die F-Statistik ausreichend groß ist, zeigt sie an, dass sich mindestens einer der Gruppenmittelwerte signifikant von den anderen unterscheidet.

Um dies besser zu verstehen, stell dir ein Szenario vor, in dem du die Leistungen (Prüfungsergebnisse) eines Schülers/einer Schülerin auf der Grundlage von drei Unterrichtsmethoden bewerten sollst: Vorlesung, interaktiver Workshop und Online-Lernen. Mit Hilfe der ANOVA können wir feststellen, ob die Unterrichtsmethode einen statistischen Einfluss auf die Prüfungsleistungen der Schüler/innen hat.

Die zwei Arten des ANOVA-Tests

Es gibt zwei Arten von ANOVA: einseitige und zweiseitige. Je nach Anzahl der unabhängigen Variablen und wie sie miteinander interagieren, werden beide in unterschiedlichen Szenarien eingesetzt.

1. Einseitige ANOVA

Ein einseitiger ANOVA-Test wird verwendet, wenn es eine unabhängige Variable mit zwei oder mehr Gruppen gibt. Das Ziel ist es, festzustellen, ob ein signifikanter Unterschied zwischen den Mittelwerten der verschiedenen Gruppen besteht.

In unserem Beispiel können wir mit der einseitigen ANOVA die Wirksamkeit der drei verschiedenen Lehrmethoden (Vorlesung, Workshop und Online-Lernen) auf die Prüfungsergebnisse der Schüler/innen vergleichen. Die Unterrichtsmethode ist die unabhängige Variable in den drei Gruppen, und die Prüfungsergebnisse sind die abhängige Variable.

• Nullhypothese (H₀): Die durchschnittlichen Prüfungsergebnisse der Schüler/innen sind bei allen drei Unterrichtsmethoden gleich (kein Unterschied in den Mittelwerten).
• Alternativhypothese (H₁): Der Mittelwert von mindestens einer Gruppe unterscheidet sich signifikant.

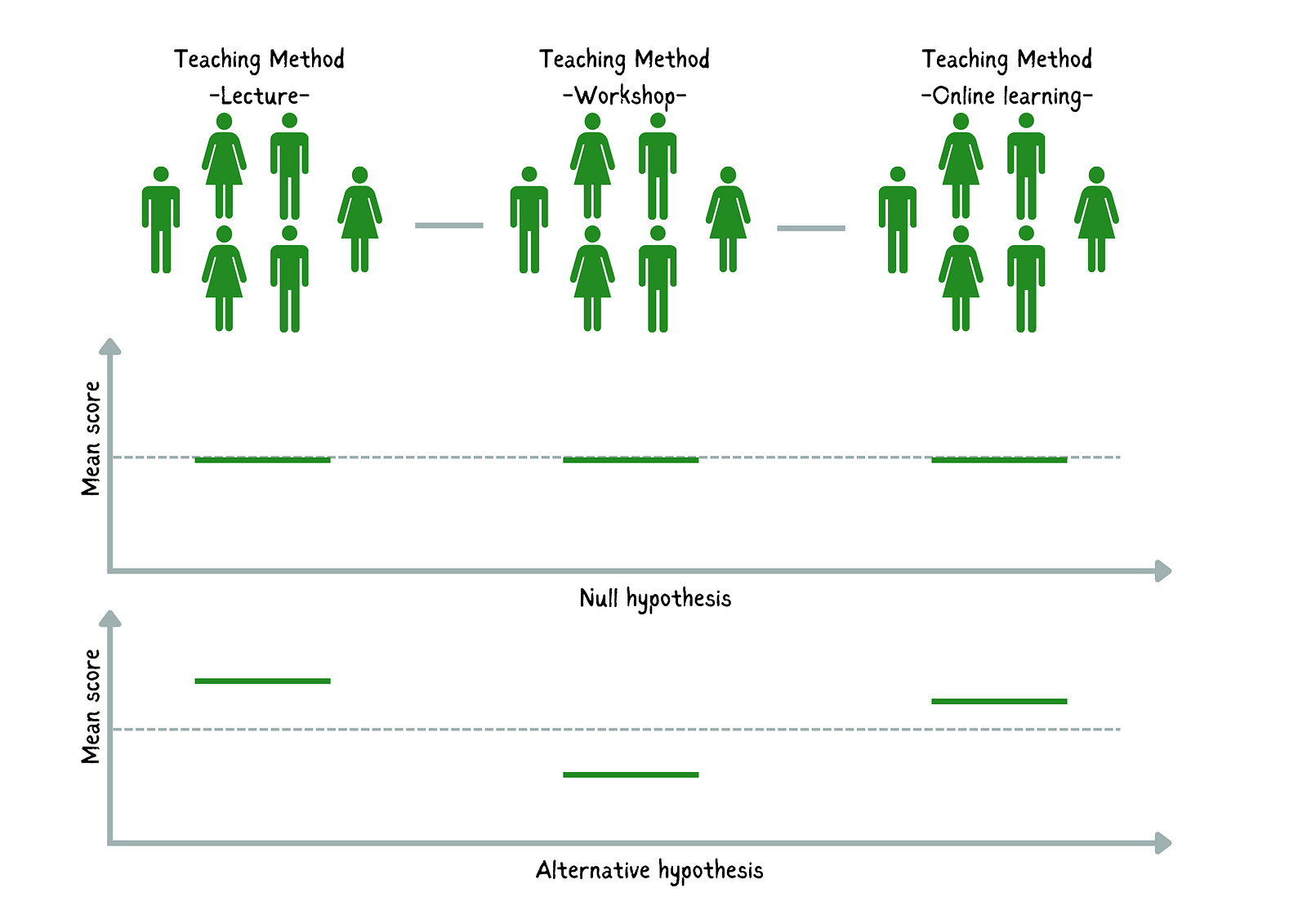Vergleich der Null- und Alternativhypothese. Bild vom Autor

Der einseitige ANOVA-Test wird uns zeigen, ob die Unterschiede in den Prüfungsergebnissen der Schüler/innen auf die unterschiedlichen Unterrichtsmethoden zurückzuführen sind oder ob es sich eher um einen Zufall handelt.

Die einseitige ANOVA ist effektiv, wenn es darum geht, die Auswirkungen eines einzelnen Faktors auf mehrere Gruppen zu analysieren, was die Interpretation vereinfacht. Sie berücksichtigt jedoch nicht die Möglichkeit von Wechselwirkungen zwischen mehreren unabhängigen Variablen, so dass eine Zwei-Wege-ANOVA notwendig wird.

2. Zwei-Wege-ANOVA

Die zweiseitige ANOVA wird verwendet, wenn es zwei unabhängige Variablen mit jeweils zwei oder mehr Gruppen gibt. Ziel ist es, zu analysieren, wie die beiden unabhängigen Variablen die abhängige Variable beeinflussen.

Nehmen wir an, du interessierst dich für die Beziehung zwischen Lehrmethoden und Lerntechniken und dafür, wie sie sich gemeinsam auf die Schülerleistungen auswirken. Die Zwei-Wege-ANOVA ist für dieses Szenario geeignet. Hier testen wir drei Hypothesen:

• Der Haupteffekt von Faktor 1 (Unterrichtsmethode): Beeinflusst die Lehrmethode die Prüfungsergebnisse der Schüler?
• Der Haupteffekt von Faktor 2 (Studientechnik): Beeinflusst die Lerntechnik die Prüfungsergebnisse?
• Interaktionseffekt: Hängt die Wirksamkeit der Unterrichtsmethode von der verwendeten Lerntechnik ab?

So könnte die ANOVA in zwei Richtungen zeigen, dass Schüler/innen, die die Vorlesungsmethode nutzen, im Gruppenstudium besser abschneiden, während diejenigen, die das Online-Lernen nutzen, im Einzelstudium besser abschneiden könnten. Das Verständnis dieser Wechselwirkungen gibt einen tieferen Einblick, wie sich verschiedene Faktoren zusammen auf die Ergebnisse auswirken.

ANOVA vs. T-Test

Du fragst dich vielleicht: Wann sollte ich eine ANOVA einem t-Test vorziehen? Der t-Test und die ANOVA werden verwendet, um Mittelwerte zwischen Gruppen zu vergleichen, aber die Wahl zwischen ihnen hängt von der Anzahl der zu vergleichenden Gruppen und der Komplexität der Datenstruktur ab.

Wann ein T-Test zu verwenden ist

Ein t-Test ist geeignet, wenn du die Mittelwerte von zwei Gruppen vergleichst. Wenn wir z.B. die Prüfungsergebnisse von Studierenden vergleichen wollten, die nur zwei Unterrichtsmethoden - Vorlesung und Workshop - anwenden, würde ein t-Test ausreichen. Es gibt zwei Arten von t-Tests:

• Unabhängiger T-Test: Vergleicht zwei unabhängige Gruppen (z.B. Vorlesung vs. Workshop).
• Gepaarter T-Test: Vergleicht die Mittelwerte derselben Gruppe zu verschiedenen Zeitpunkten (z. B. die Leistungen der Schüler/innen vor und nach der Anwendung einer bestimmten Unterrichtsmethode).

Wann wird die ANOVA verwendet?

Andererseits wird die ANOVA verwendet, wenn die Mittelwerte von drei oder mehr Gruppen verglichen werden. Unsere Studie umfasst drei Lehrmethoden (Vorlesung, Workshop und Online-Lernen), daher ist mehr als ein t-Test erforderlich. Die Verwendung mehrerer t-Tests für jedes Gruppenpaar würde das Risiko eines Fehlers vom Typ I (falsch-positive Ergebnisse) erhöhen, während die ANOVA den Vergleich in einem einzigen Test durchführt und diesen Fehler kontrolliert.

ANOVA-Test Annahmen

Alle statistischen Tests haben Annahmen, die erfüllt sein müssen, um gültige Ergebnisse zu erzielen. 

Hier sind die Annahmen, die für die ANOVA erfüllt sein müssen:

1. Unabhängigkeit der Beobachtungen

Die Beobachtungen (Datenpunkte) müssen unabhängig voneinander sein. In dem Beispiel sollten die Prüfungsergebnisse der Schüler in einer Unterrichtsmethode die Ergebnisse der Schüler in einer anderen Methode nicht beeinflussen.

2. Homogenität der Varianzen

Die Varianzen innerhalb jeder Gruppe sollten ungefähr gleich sein. Bei der ANOVA wird davon ausgegangen, dass die Variabilität der Prüfungsergebnisse innerhalb jeder Lehrmethodengruppe ungefähr gleich groß ist. Dies kann mit dem Levene-Test überprüft werden, der auf gleiche Varianzen prüft.

3. Normalverteilung

Die Daten innerhalb jeder Gruppe sollten einer Normalverteilung folgen. In unserem Beispiel für eine Unterrichtsmethode sollten die Prüfungsergebnisse der Schüler/innen in jeder Unterrichtsgruppe (Vorlesung, Workshop, Online-Lernen) idealerweise normalverteilt sein.

Wenn irgendwelche Annahmen verletzt werden, können die Testergebnisse ungültig sein. In solchen Fällen ist es wichtig, einen nicht-parametrischen Test zu verwenden.

Durchführen eines ANOVA-Tests

Anhand des gleichen Beispiels werden wir verschiedene Unterrichtsmethoden vergleichen und untersuchen, wie sie sich auf die Prüfungsergebnisse der Schüler/innen auswirken. Nehmen wir an, dir liegen die folgenden Daten vor, die die Prüfungsergebnisse (abhängige Variable) in Abhängigkeit von der Unterrichtsmethode (unabhängige Variable) zeigen.

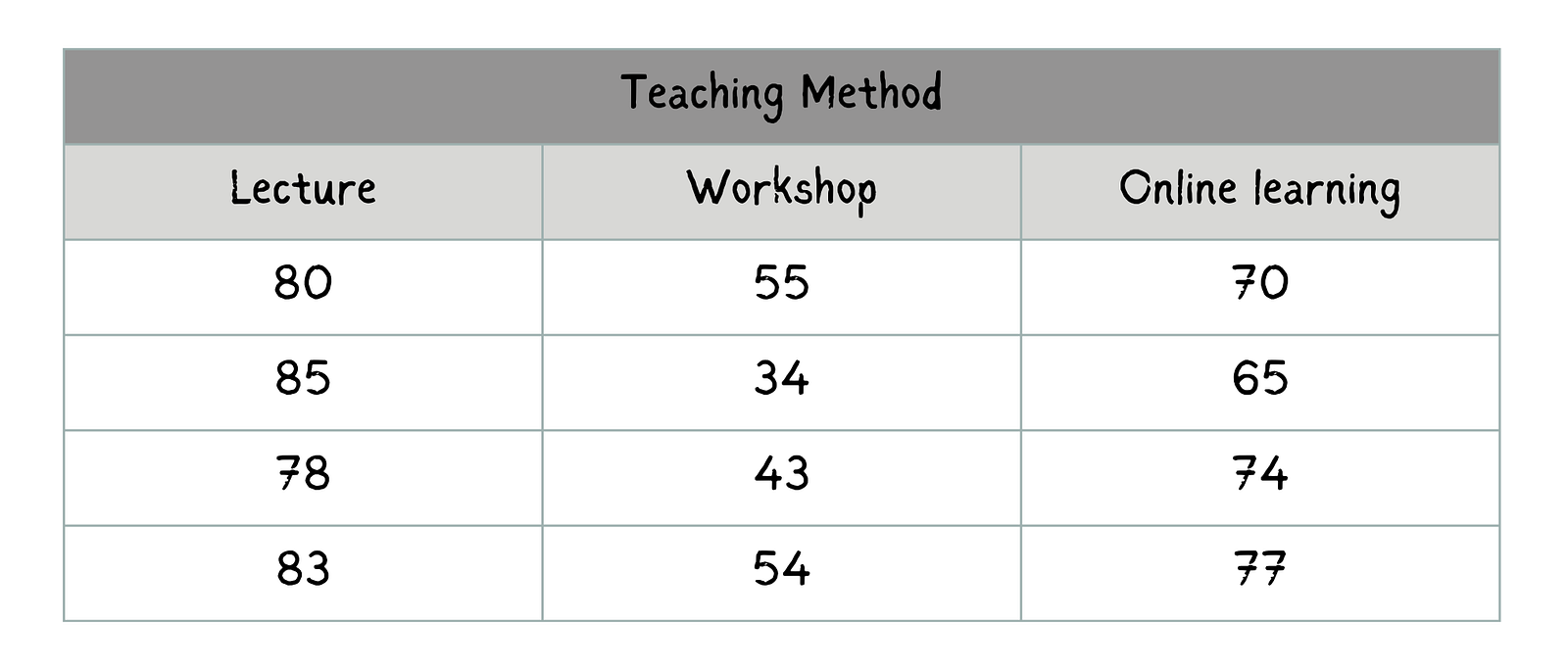Prüfungsergebnisse für jede Unterrichtsmethode für jeweils vier Schüler/innen. Bild vom Autor

Schritt 1: Definiere die Hypothese

Der erste Schritt im Prozess ist die Festlegung der Hypothese. Gib die Null- und Alternativhypothese an:

• Nullhypothese (H₀): Die Mittelwerte der Prüfungsergebnisse der Schüler in den drei Unterrichtsmethoden sind gleich.
• Alternativhypothese (H₁): Mindestens eine Unterrichtsmethode hat eine andere durchschnittliche Prüfungsnote.

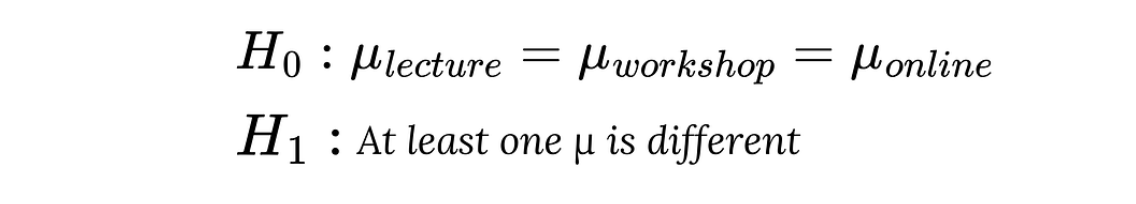
Nullhypothese und Alternativhypothese. Bild vom Autor

Schritt 2: ANOVA-Annahmen prüfen

Bevor du eine ANOVA durchführst, stelle sicher, dass die Annahmen erfüllt sind. Normalität, Unabhängigkeit und Homogenität der Varianzen. Der Einfachheit halber gehen wir davon aus, dass alle Annahmen erfüllt sind.

Schritt 3: ANOVA berechnen

Wenn die Annahmen überprüft sind, berechne die ANOVA.

Die Formel für die F-Statistik bei der einseitigen ANOVA lautet wie folgt.

F-Statistik in einseitiger ANOVA. Bild vom Autor

Die F-Statistik bei der einseitigen ANOVA ist das Verhältnis zwischen der mittleren Quadratsumme zwischen den Gruppen und der mittleren Quadratsumme innerhalb der Gruppen.

Um das zu erreichen, gehen wir Schritt für Schritt vor.

1. Berechne den Mittelwert für jede Gruppe und den Gesamtmittelwert.

Berechne mit der folgenden Gleichung den Mittelwert für jede Unterrichtsmethode (Ai). Teile die Summe der Prüfungsergebnisse für jede Gruppe durch die Anzahl der Schüler/innen in jeder Gruppe.

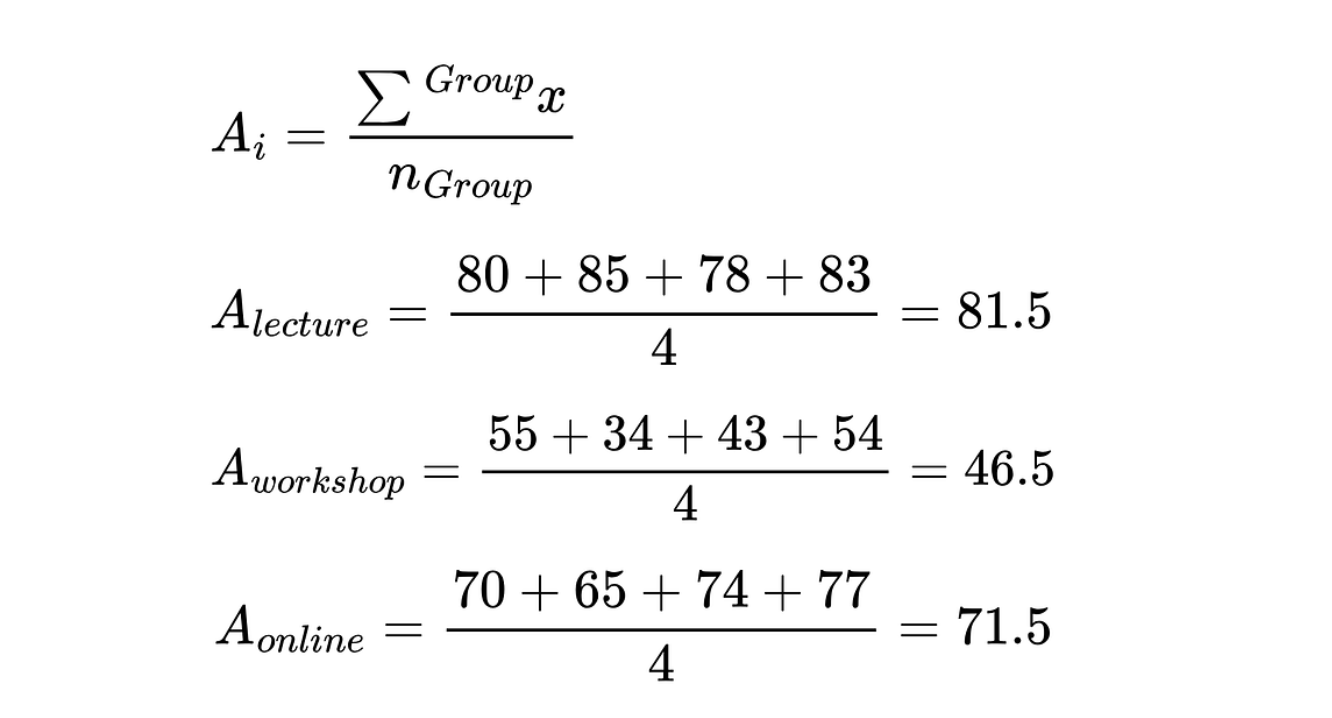
Mittelwert für jede Gruppe (Unterrichtsmethode). Bild vom Autor

Berechne dann den Gesamtmittelwert (G), indem du die Summe aller Instanzen durch die Gesamtzahl der Schüler/innen teilst.

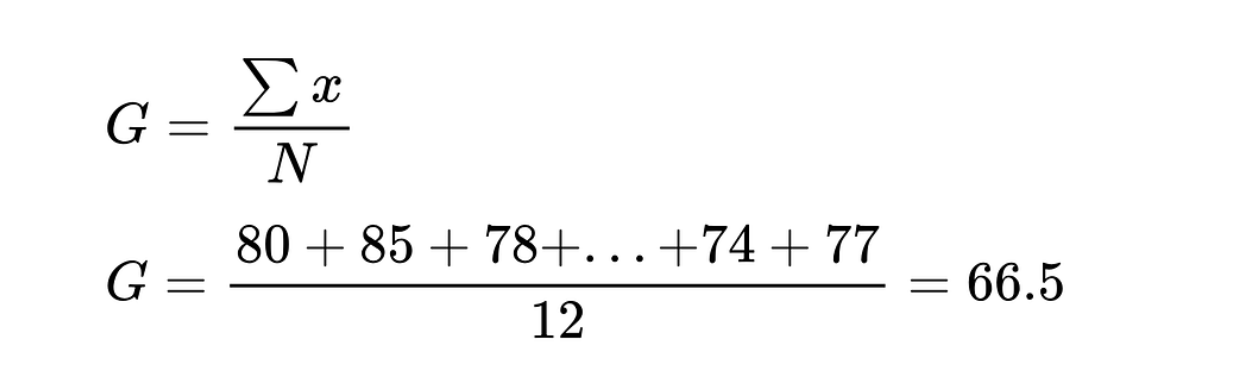
Gesamtdurchschnitt der Prüfungsergebnisse. Bild vom Autor

2. Berechne die Summe der Quadrate für jede Gruppe

Die Gleichung lautet wie folgt, um die Summe der Quadrate für jede Gruppe zu berechnen.

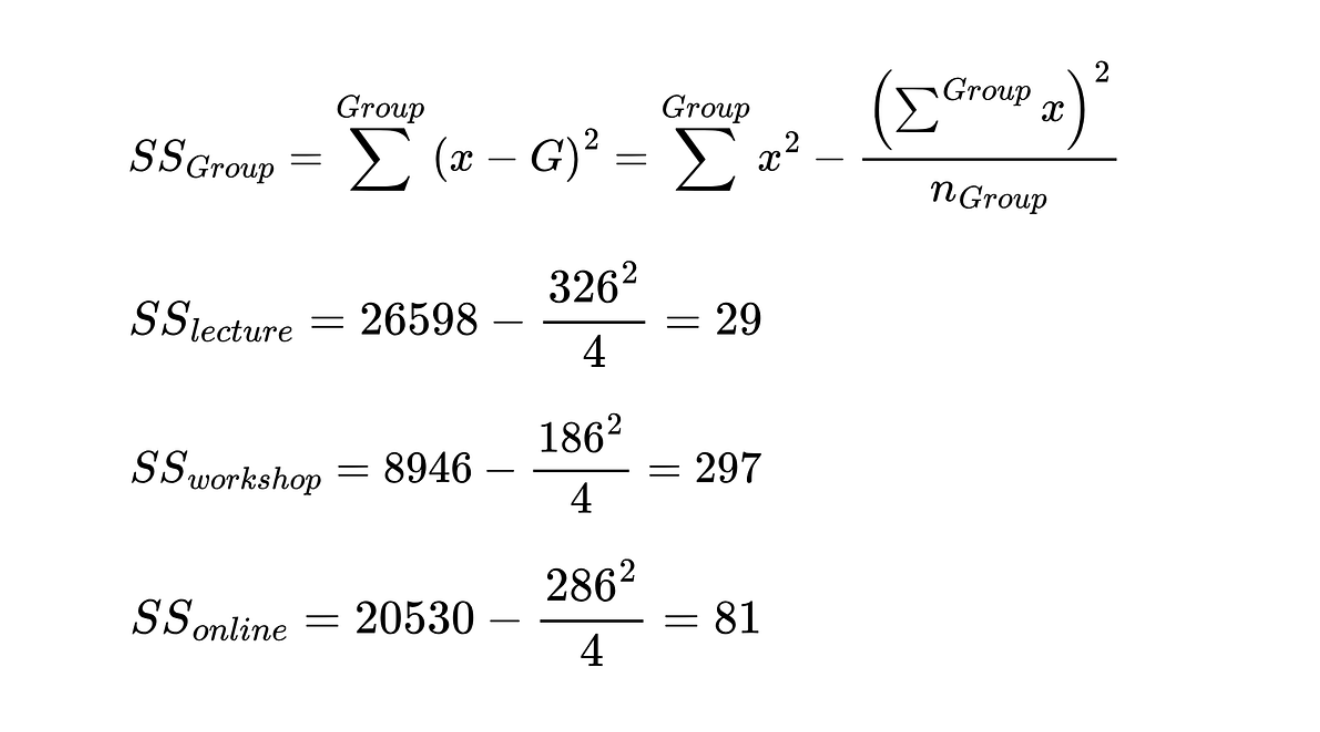
Die Summe der Quadrate für jede Unterrichtsmethode. Bild vom Autor

Nach der Berechnung füllst du diese Tabelle mit den Werten aus, damit sie leicht zugänglich sind.

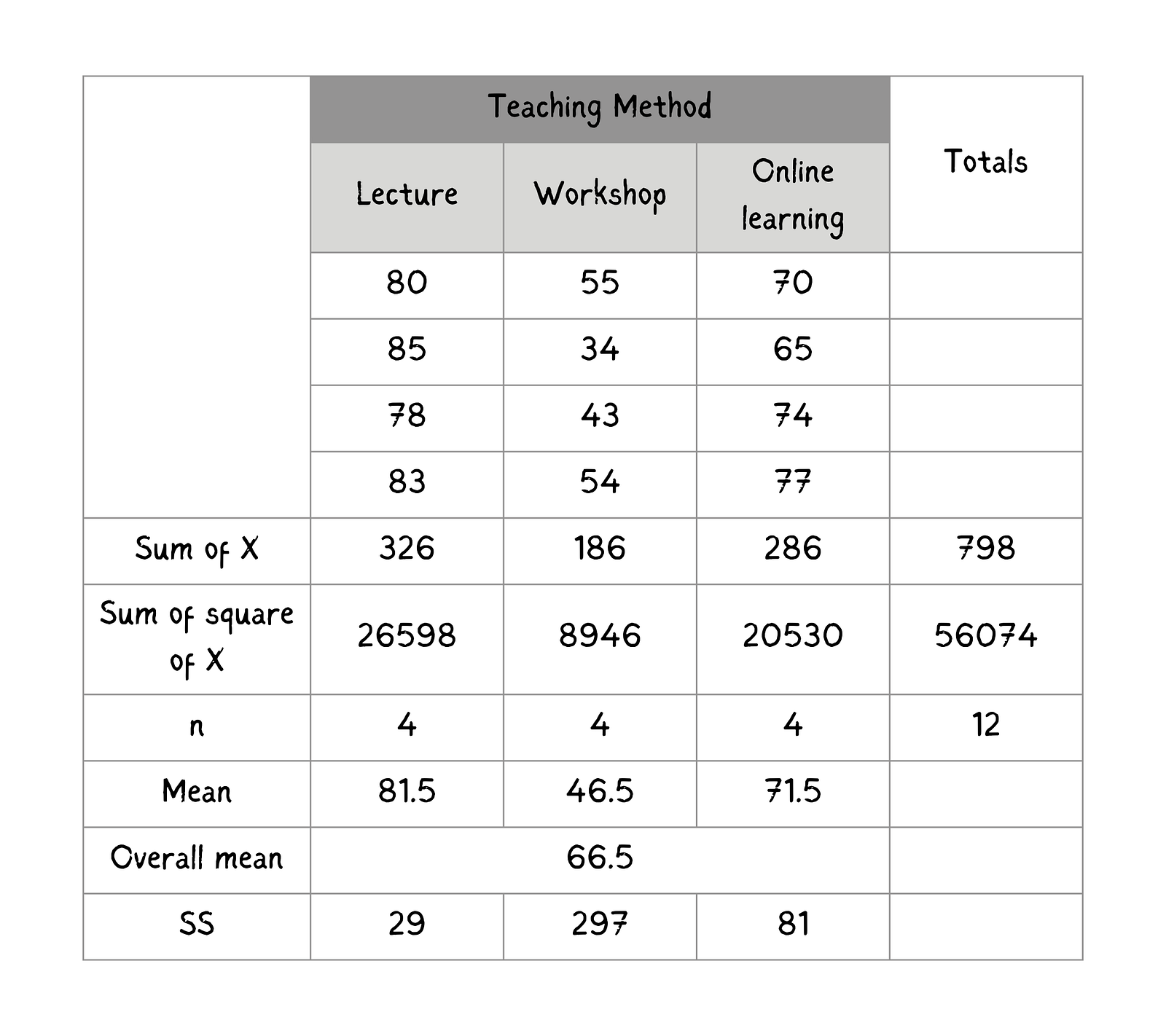Zusammenfassung der Schülerleistungen nach Unterrichtsmethode. Bild vom Autor

3. Berechne die Summe der Quadrate zwischen den Gruppen, die Summe der Quadrate innerhalb der Gruppe und die Gesamtsumme der Quadrate.

Berechne mithilfe der folgenden Gleichung die Summe der Quadrate zwischen den Gruppen. In der Gleichung,

• Ai: Mittelwert der Gruppe
• G: Gesamtmittelwert
• ni: Anzahl der Instanzen in jeder Gruppe

Verwende für die Berechnung die Werte aus der Übersichtstabelle.

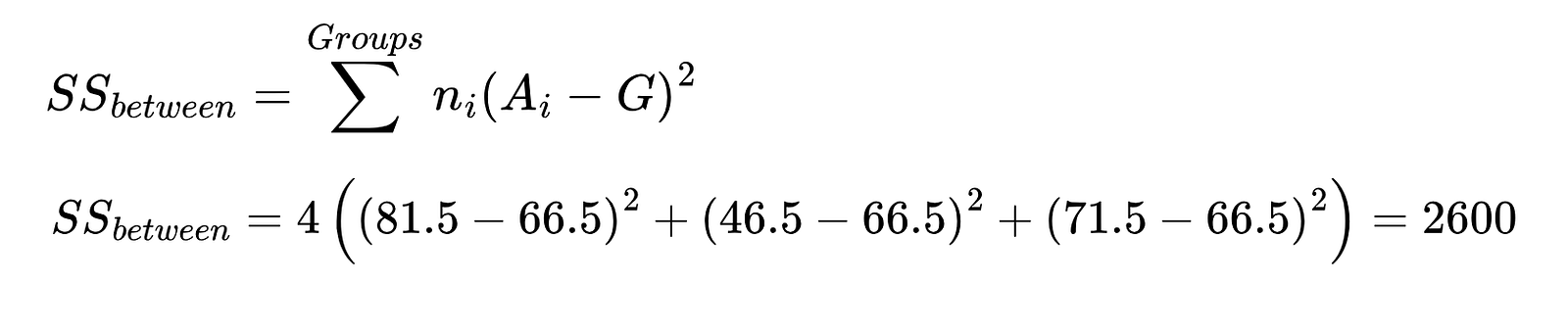Summe der Quadrate zwischen der Gruppe

Als Nächstes berechnest du die Summe der Quadrate innerhalb der Gruppe. Sie ist die Summe der Quadrate (SS) für jede Gruppe.

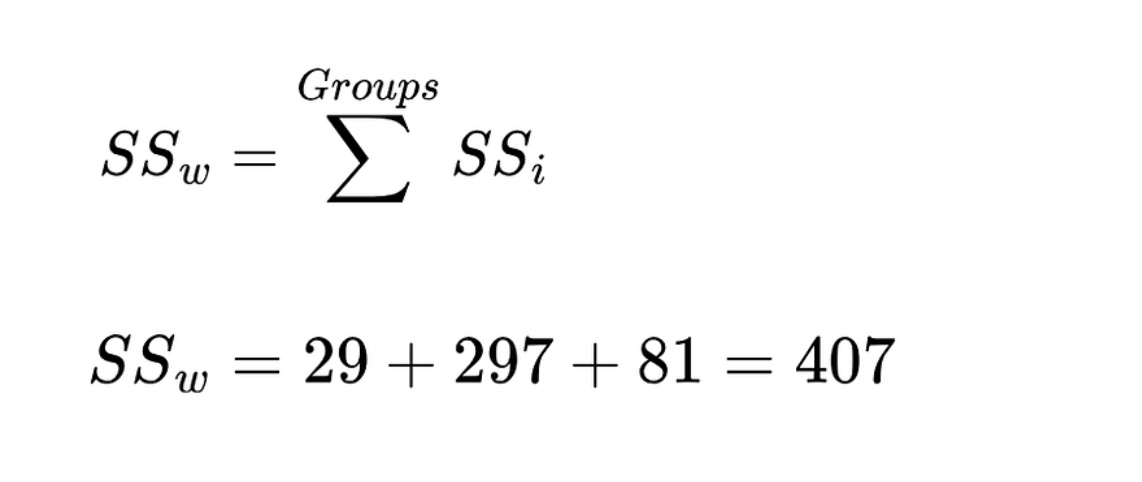
Summe der Quadrate innerhalb der Gruppe. Bild vom Autor

Verwende die folgende Gleichung, um die Gesamtsumme der Quadrate zu berechnen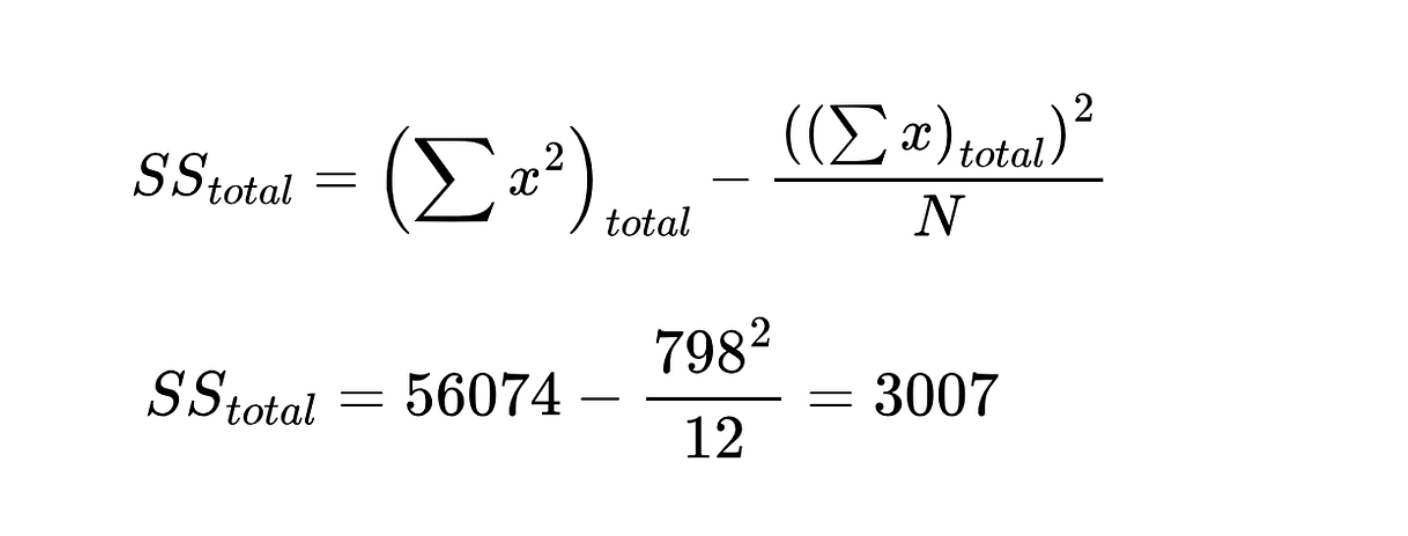
Gesamtsumme der Quadrate. Bild vom Autor

Überprüfe die Berechnung, indem du nachsiehst, ob die Gesamtsumme der Quadrate die Summe der Quadrate zwischen den Gruppen und die Summe der Quadrate innerhalb der Gruppe ist. Nach der Überprüfung kannst du mit der Berechnung der mittleren Quadrate fortfahren.

4. Berechne die mittleren Quadrate

Die mittleren Quadrate sind das Verhältnis der Quadratsummen zum Freiheitsgrad.

Der Freiheitsgrad zwischen den Gruppen df_between ist gleich der Anzahl der Gruppen minus eins, und der Freiheitsgrad innerhalb der Gruppen df_w ist gleich der Gesamtzahl der Teilnehmer minus der Anzahl der Gruppen.

Berechne mit den im vorherigen Schritt berechneten Werten die mittleren Quadrate.

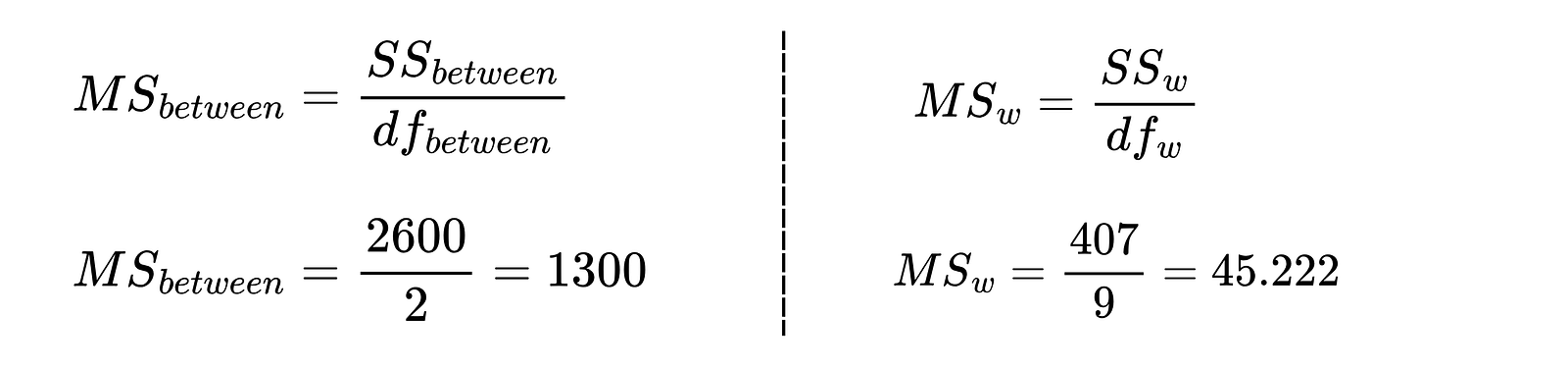Mittlere Quadrate zwischen den Gruppen und innerhalb der Gruppen. Bild vom Autor

5. Berechne die F-Statistik anhand der folgenden Gleichung

Die F-Statistik ist das Verhältnis des mittleren Quadrats zwischen den Gruppen zum mittleren Quadrat innerhalb der Gruppe.

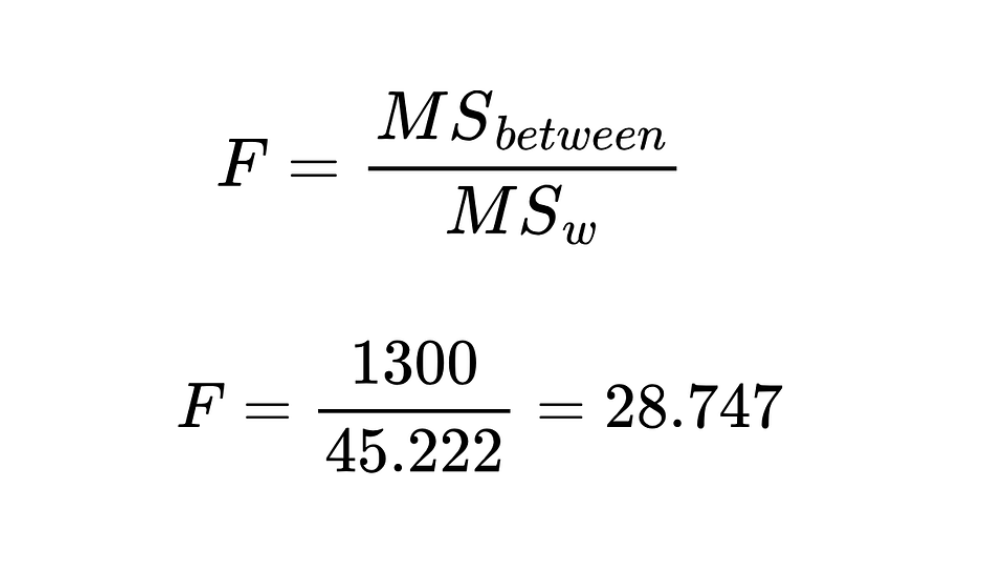
F-Statistik. Bild vom Autor

Der berechnete Wert der F-Statistik beträgt 28,747.

Schließlich wird der p-Wert anhand der F-Statistik, des Freiheitsgrads df und der F-Verteilungstabelle berechnet.

In diesem Beispiel ist der Zähler df 2, der Nenner df ist 9 und die F-Statistik ist 28,747. Daher ist der p-Wert aus der F-Verteilungstabelle 0,000123.

Schritt 4: Interpretiere die Ergebnisse

• F-statistic: Die F-Statistik misst das Verhältnis der Variation zwischen den Gruppen zur Variation innerhalb der Gruppen. Eine höhere F-Statistik zeigt an, dass der Unterschied zwischen den Gruppenmitteln größer ist als die zufällige Variation.
• P-value: Der p-Wert bestimmt, ob die Unterschiede zwischen den Gruppenmitteln statistisch signifikant sind. Liegt der p-Wert unter einem festgelegten Schwellenwert (in der Regel 0,05), lehne die Nullhypothese ab und schließe daraus, dass mindestens eine Gruppe einen signifikant unterschiedlichen Mittelwert hat.

Der p-Wert beträgt 0,000123. Wir würden die Nullhypothese ablehnen und zu dem Schluss kommen, dass die Lehrmethode die Prüfungsergebnisse signifikant beeinflusst.

Post-Hoc-Tests nach ANOVA

Die ANOVA sagt uns, ob es einen statistisch signifikanten Unterschied zwischen den Gruppenmitteln gibt, aber sie gibt nicht an, welche Gruppen sich signifikant voneinander unterscheiden. Das ist die Aufgabe von Post-Hoc-Tests - sie führen paarweise Vergleiche zwischen den Gruppen durch, um genau festzustellen, wo die Unterschiede liegen. Wenn du mehr als zwei Gruppen hast, sind diese Tests unverzichtbar, und das ANOVA-Ergebnis ist signifikant.

Um unser Beispiel fortzusetzen, zeigt der Test einen signifikanten Unterschied in den Prüfungsergebnissen der Schüler/innen nach Durchführung der einseitigen ANOVA für die drei Unterrichtsmethoden (Vorlesung, Workshop und Online-Lernen). Ein Post-Hoc-Test wird uns helfen herauszufinden, welche Unterrichtsmethoden sich unterschiedlich auf die Prüfungsleistungen auswirken.

Tukey's Honestly Significant Difference (HSD) und Bonferroni-Korrektur sind weit verbreitete Post-hoc-Tests.

Alternativen zur ANOVA

Wenn die Annahmen der ANOVA nicht erfüllt sind oder die ANOVA für den Datensatz nicht geeignet ist, kannst du die folgenden Alternativen in Betracht ziehen.

1. Kruskal-Wallis Test: Sie ist eine nicht-parametrische Alternative zur einseitigen ANOVA, wenn die Normalitätsannahme verletzt ist. Er ist eine erweiterte Version des Mann-Whitney-U-Tests.
2. MANOVA (Multivariate Varianzanalyse): Sie erweitert die Prinzipien der ANOVA auf mehrere abhängige Variablen. Sie prüft, ob sich die Mittelwertvektoren mehrerer abhängiger Variablen zwischen den Gruppen unterscheiden.

Fazit

In diesem Artikel wurden die wichtigsten Konzepte der ANOVA vorgestellt und aufgezeigt, wann sie im Vergleich zum t-Test eingesetzt werden sollte. Wir haben gelernt, dass die ANOVA eine robuste statistische Analyse ist, die mehrere Gruppen gleichzeitig vergleicht. Wir haben eine Schritt-für-Schritt-Anleitung zur Durchführung der ANOVA erstellt, in der wir detailliert beschreiben, wie man Hypothesen formuliert, Annahmen überprüft und Ergebnisse interpretiert.

Um praktische Erfahrungen mit der ANOVA in Excel zu sammeln, schau dir das Tutorial Comprehensive Guide to Using ANOVA in Excel an. Erwäge, die Kurse Foundations of Inference in Python und Inferential Statistics zu belegen, um dein Wissen über Statistik zu erweitern.