Teste ANOVA: Um guia detalhado com exemplos

A ANOVA oferece uma maneira de testar se há diferenças significativas entre as médias dos grupos, ajudando os pesquisadores a determinar se a variação nos dados se deve a diferenças reais entre os grupos ou apenas ao acaso. Esse método é útil ao lidar com experimentos ou estudos que envolvem mais de dois grupos, nos quais os testes t tradicionais podem não ser adequados ou eficientes.

Este artigo explorará os fundamentos do teste ANOVA, sua finalidade, os dois principais tipos e um guia passo a passo para você realizar o ANOVA. A compreensão desses conceitos pode ajudar você a escolher o teste correto para seus dados e a interpretar os resultados com confiança. Também consideraremos um exemplo para que você entenda melhor o conceito. Se você ainda não conhece a ideia de teste de hipóteses em geral, leia nosso artigo Teste de hipóteses facilitado para você.

O que é um teste ANOVA?

ANOVA significa Analysis of Variance (Análise de Variância), um teste estatístico usado para comparar as médias de três ou mais grupos. Ele analisa a variação dentro do grupo e entre os grupos. O objetivo principal é avaliar se a variação observada entre as médias dos grupos é mais significativa do que dentro dos grupos. Se a variação observada entre as médias do grupo for significativa, isso sugere que as diferenças são significativas.

Matematicamente, a ANOVA divide a variabilidade total dos dados em dois componentes:

• Variabilidade dentro do grupo: Variabilidade causada por diferenças dentro de grupos individuais, refletindo flutuações aleatórias.
• Variabilidade entre grupos: Variabilidade causada por diferenças entre as médias dos diferentes grupos.

Estatística F para calcular a ANOVA. Imagem do autor

O teste produz uma estatística F, que mostra a relação entre a variabilidade entre o grupo e a variabilidade dentro do grupo. Se a estatística F for suficientemente grande, isso indica que pelo menos uma das médias do grupo é significativamente diferente das outras.

Para entender isso melhor, considere um cenário em que você é solicitado a avaliar o desempenho de um aluno (notas de exames) com base em três métodos de ensino: aula expositiva, workshop interativo e aprendizagem on-line. A ANOVA pode nos ajudar a avaliar se o método de ensino afeta estatisticamente o desempenho do aluno no exame.

Os dois tipos de teste ANOVA

Há dois tipos de ANOVA: unidirecional e bidirecional. Dependendo do número de variáveis independentes e de como elas interagem umas com as outras, ambas são usadas em cenários diferentes.

1. ANOVA unidirecional

Um teste ANOVA unidirecional é usado quando há uma variável independente com dois ou mais grupos. O objetivo é determinar se existe uma diferença significativa entre as médias de diferentes grupos.

Em nosso exemplo, podemos usar a ANOVA unidirecional para comparar a eficácia dos três métodos de ensino diferentes (palestra, workshop e aprendizado on-line) nas pontuações dos exames dos alunos. O método de ensino é a variável independente com três grupos, e a pontuação do exame é a variável dependente.

• Hipótese nula (H₀): As pontuações médias dos exames dos alunos nos três métodos de ensino são iguais (sem diferença nas médias).
• Hipótese alternativa (H₁): A média de pelo menos um grupo difere significativamente.

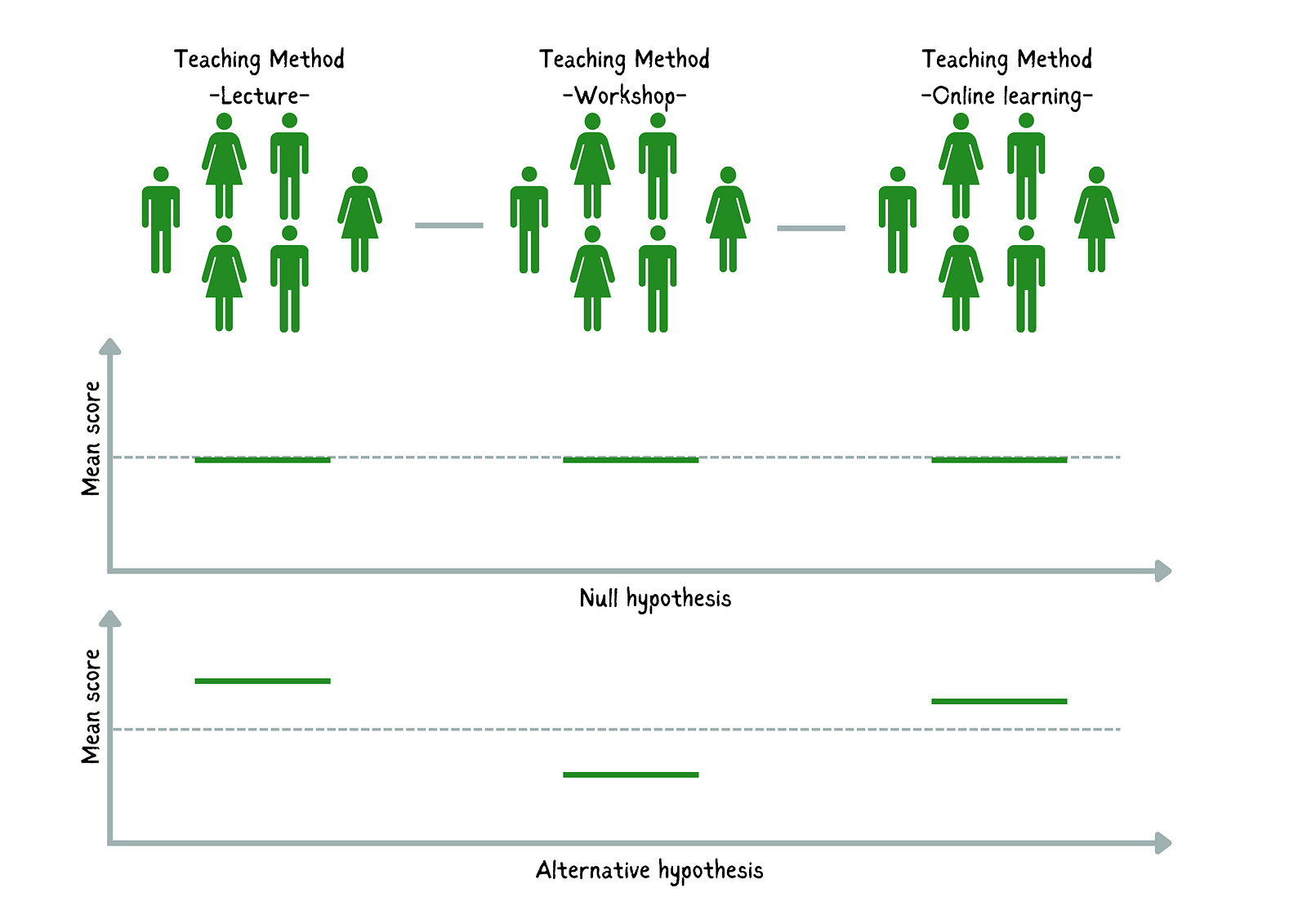Comparação das hipóteses nula e alternativa. Imagem do autor

O teste ANOVA unidirecional nos dirá se a variação nas pontuações dos exames dos alunos pode ser atribuída às diferenças nos métodos de ensino ou se é provável que seja devido ao acaso.

A ANOVA unidirecional é eficaz ao analisar o impacto de um único fator em vários grupos, o que simplifica a interpretação. No entanto, ela não leva em conta a possibilidade de interação entre várias variáveis independentes, o que torna necessária a ANOVA de duas vias.

2. ANOVA de duas vias

A ANOVA de duas vias é usada quando há duas variáveis independentes, cada uma com dois ou mais grupos. O objetivo é analisar como as duas variáveis independentes influenciam a variável dependente.

Vamos supor que você esteja interessado na relação entre métodos de ensino e técnicas de estudo e como eles afetam conjuntamente o desempenho do aluno. A ANOVA de duas vias é adequada para esse cenário. Aqui testamos três hipóteses:

• O principal efeito do fator 1 (método de ensino): O método de ensino influencia as pontuações dos alunos nos exames?
• O principal efeito do fator 2 (técnica de estudo): A técnica de estudo afeta as notas do exame?
• Efeito de interação: A eficácia do método de ensino depende da técnica de estudo utilizada?

Por exemplo, a ANOVA de duas vias poderia revelar que os alunos que usam o método de aula expositiva têm melhor desempenho no estudo em grupo, enquanto os que usam o aprendizado on-line podem ter melhor desempenho no estudo individual. A compreensão dessas interações proporciona uma visão mais profunda de como os diferentes fatores juntos afetam os resultados.

ANOVA vs. Teste T

Você pode estar se perguntando: Quando devo escolher uma ANOVA em vez de um teste t? O teste t e a ANOVA são usados para comparar médias entre grupos, mas a escolha entre eles depende do número de grupos que estão sendo comparados e da complexidade da estrutura de dados.

Quando usar o teste T

O teste t é adequado para comparar as médias de dois grupos. Por exemplo, se quiséssemos comparar as pontuações dos exames dos alunos usando apenas dois métodos de ensino - aula expositiva e workshop - um teste t seria suficiente. Há dois tipos de testes t:

• Teste T independente: Compara dois grupos independentes (por exemplo, palestra vs. workshop).
• Teste T pareado: Compara médias do mesmo grupo em momentos diferentes (por exemplo, o desempenho do aluno antes e depois de usar um determinado método de ensino).

Quando usar a ANOVA

Por outro lado, a ANOVA é usada para comparar as médias de três ou mais grupos. Nosso estudo inclui três métodos de ensino (palestra, workshop e aprendizagem on-line), portanto, é necessário algo mais do que um teste t. O uso de vários testes t para cada par de grupos aumentaria o risco de erro do Tipo I (falsos positivos), ao passo que a ANOVA lida com a comparação em um único teste e controla esse erro.

Premissas do teste ANOVA

Todos os testes estatísticos têm suposições que devem ser atendidas para garantir resultados válidos. 

Aqui estão as suposições que precisam ser satisfeitas para a ANOVA:

1. Independência das observações

As observações (pontos de dados) devem ser independentes umas das outras. No exemplo, as notas dos exames dos alunos em um método de ensino não devem influenciar as notas dos alunos em outro método.

2. Homogeneidade de variâncias

As variações dentro de cada grupo devem ser aproximadamente iguais. A ANOVA pressupõe que a variabilidade das pontuações dos exames em cada grupo de método de ensino é praticamente a mesma. Isso pode ser testado usando o teste de Levene, que verifica se as variâncias são iguais.

3. Distribuição normal

Os dados de cada grupo devem seguir uma distribuição normal. Em nosso exemplo de método de ensino, as pontuações dos exames para os alunos em cada grupo de ensino (Palestra, Workshop, Aprendizagem on-line) devem ser distribuídas normalmente.

Se alguma suposição for violada, os resultados do teste poderão ser inválidos. Nesses casos, é essencial considerar o uso de um teste não paramétrico.

Execução de um teste ANOVA

Usaremos o mesmo exemplo de comparação de diferentes métodos de ensino para examinar como eles afetam as pontuações dos alunos nos exames. Vamos supor que você tenha os seguintes dados mostrando as pontuações dos exames (variável dependente) com base no método de ensino (variável independente).

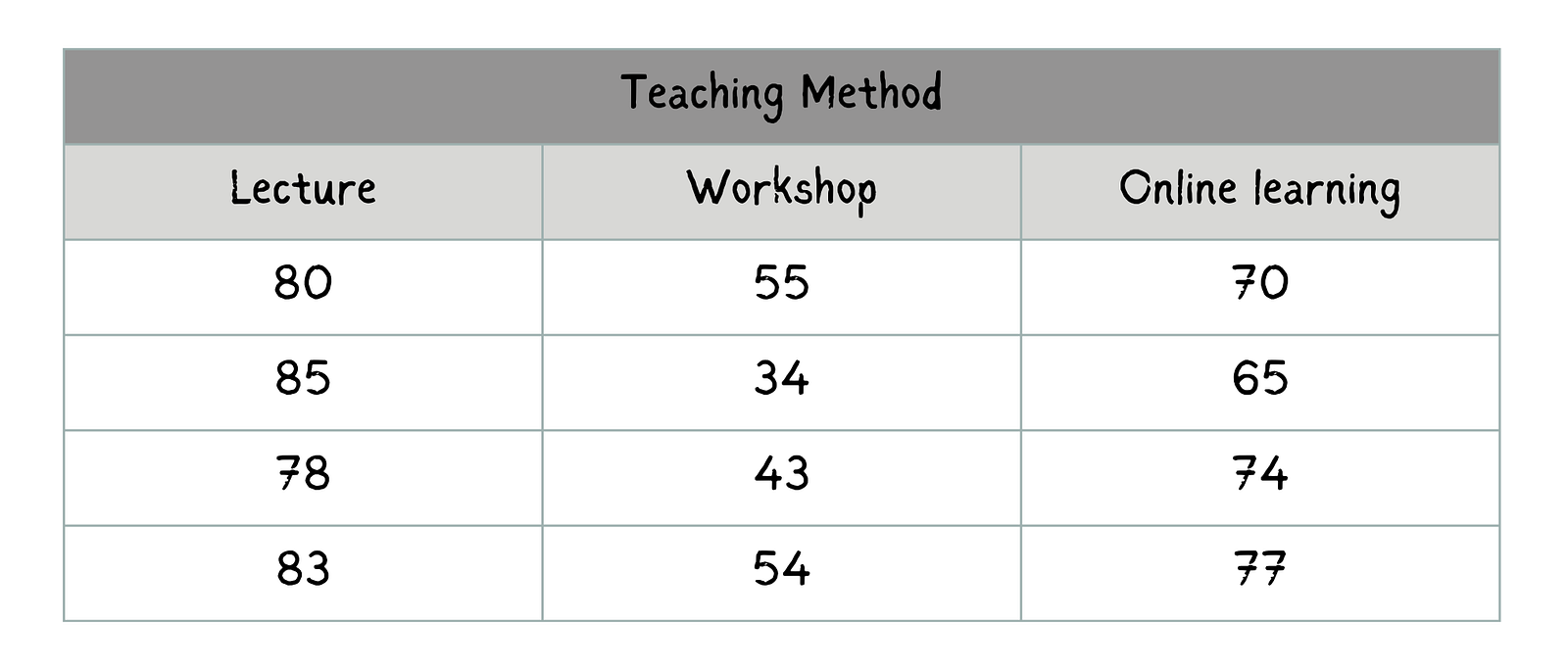de cadaPontuações de exames para cada método de ensino para quatro alunos cada. Imagem do autor

Etapa 1: Definir a hipótese

A primeira etapa do processo é definir a hipótese. Indique as hipóteses nula e alternativa:

• Hipótese nula (H₀): As médias das notas dos exames dos alunos nos três métodos de ensino são iguais.
• Hipótese alternativa (H₁): Pelo menos um método de ensino tem uma pontuação média diferente no exame.

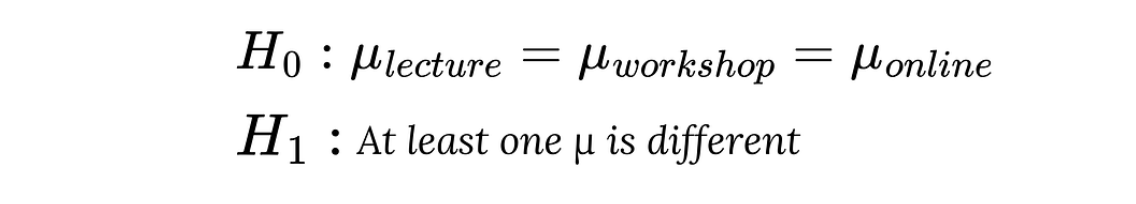
Hipótese nula e hipótese alternativa. Imagem do autor

Etapa 2: Verificar as premissas da ANOVA

Antes de executar a ANOVA, certifique-se de que as premissas sejam atendidas. Normalidade, independência e homogeneidade das variações. Para simplificar, vamos supor que todas as premissas sejam atendidas.

Etapa 3: Calcular ANOVA

Depois que as suposições forem verificadas, calcule a ANOVA.

A fórmula para a estatística F em uma ANOVA unidirecional é definida abaixo.

Estatística F em ANOVA unidirecional. Imagem do autor

A estatística F em uma ANOVA unidirecional é a razão entre a soma quadrada média entre os grupos e a soma quadrada média dentro dos grupos.

Para chegar a isso, vamos seguir o passo a passo.

1. Calcule a média de cada grupo e a média geral.

Use a equação abaixo para calcular a média de cada método de ensino (Ai). Divida a soma das pontuações dos exames de cada grupo pelo número de alunos em cada grupo.

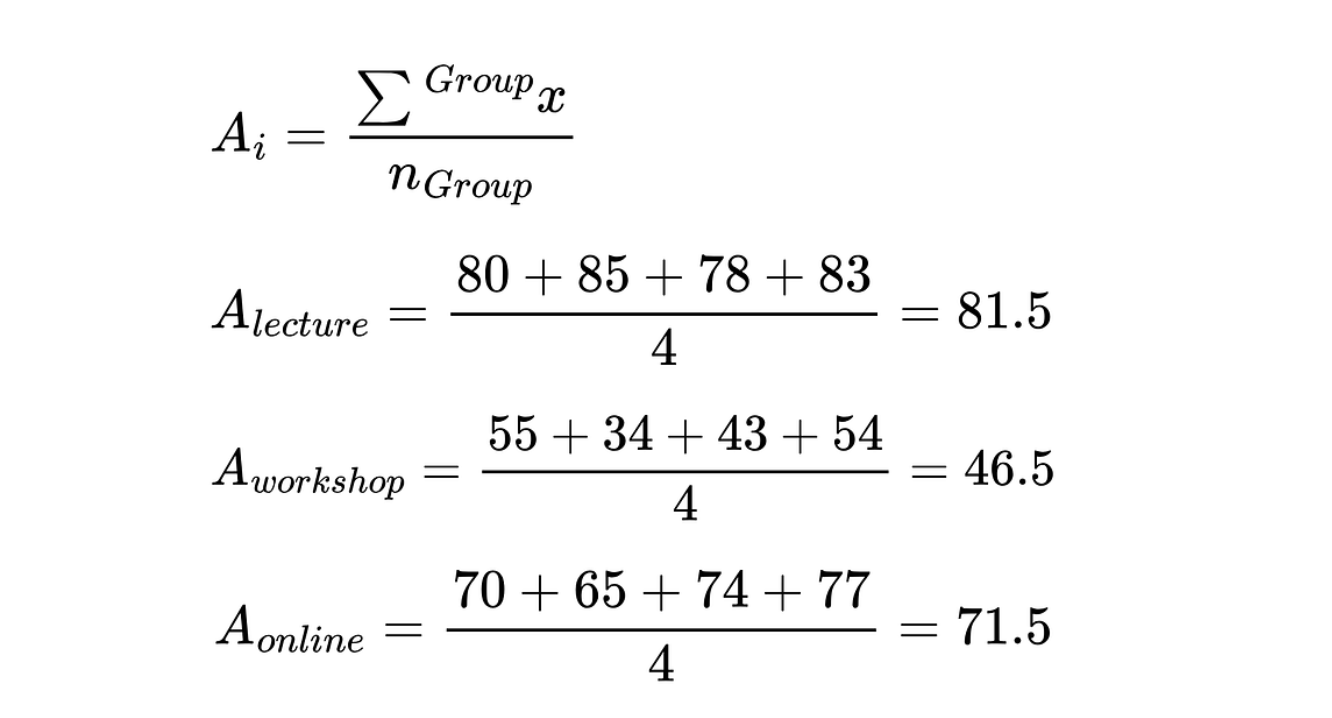
Média para cada grupo (método de ensino). Imagem do autor

Em seguida, calcule a média geral (G) dividindo a soma de todas as instâncias pelo número total de alunos.

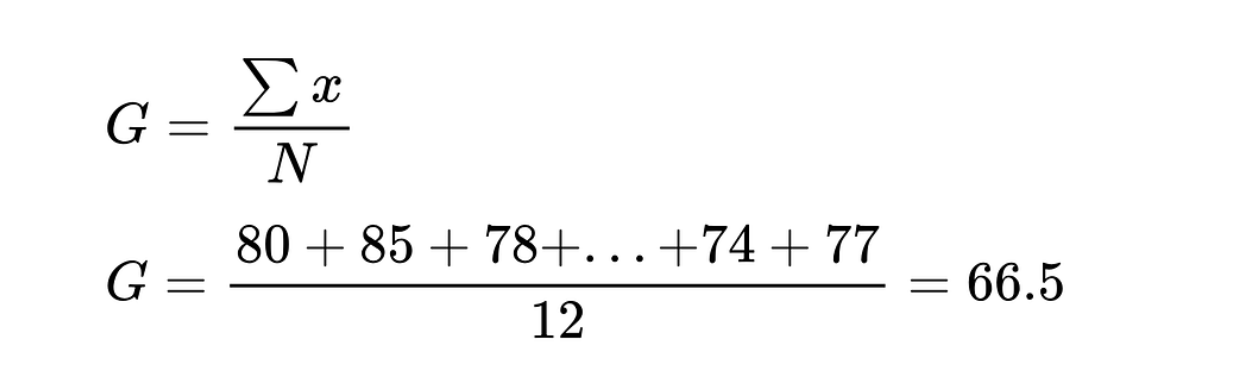
Média geral das pontuações dos exames. Imagem do autor

2. Calcule a soma dos quadrados para cada grupo

A equação é a seguinte para calcular a soma dos quadrados de cada grupo.

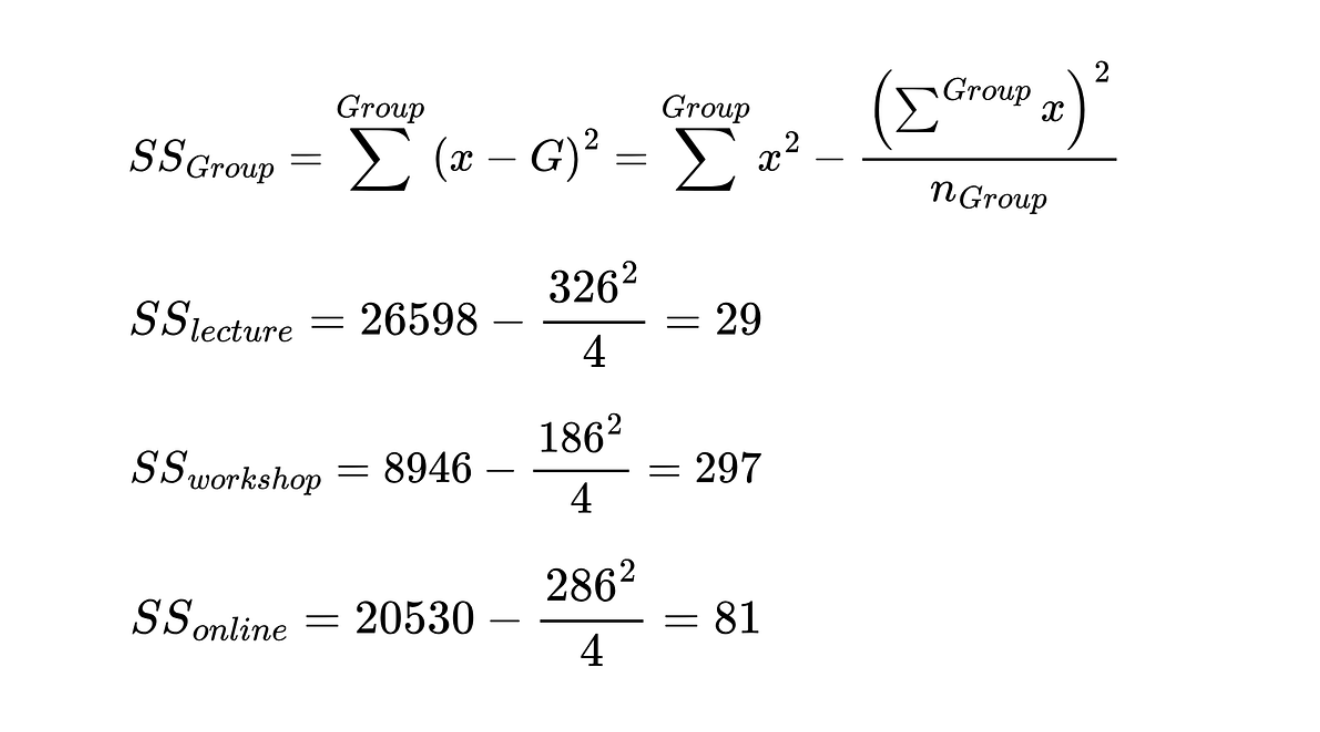
A soma dos quadrados para cada método de ensino. Imagem do autor

Após o cálculo, preencha essa tabela com os valores para facilitar o acesso.

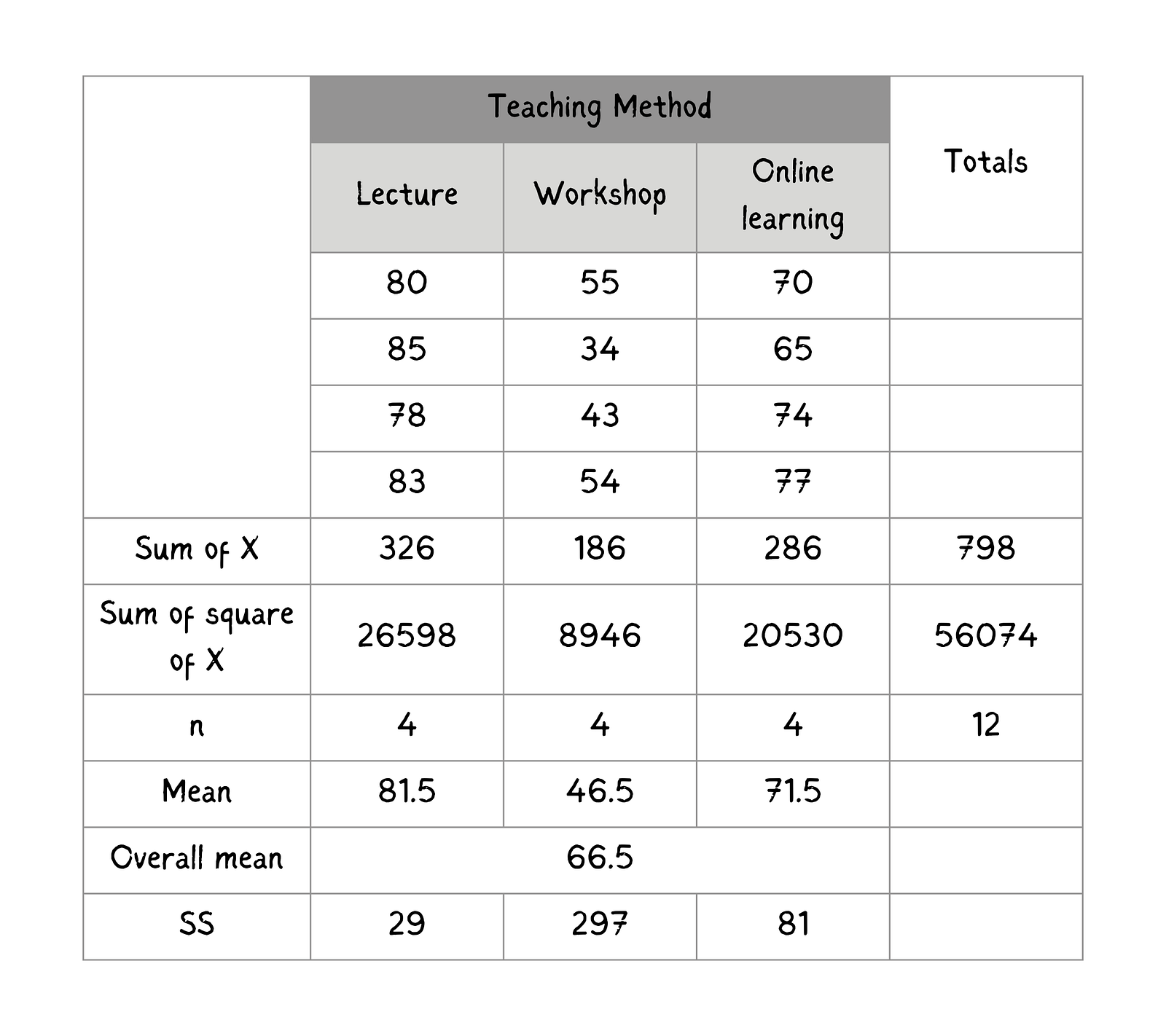Resumo do desempenho dos alunos por método de ensino. Imagem do autor

3. Calcule a soma dos quadrados entre o grupo, a soma dos quadrados dentro do grupo e a soma total dos quadrados.

Usando a equação abaixo, calcule a soma dos quadrados entre os grupos. Na equação,

• Ai: Média do grupo
• G: Média geral
• niNúmero de instâncias em cada grupo

Use os valores da tabela de resumo para o cálculo.

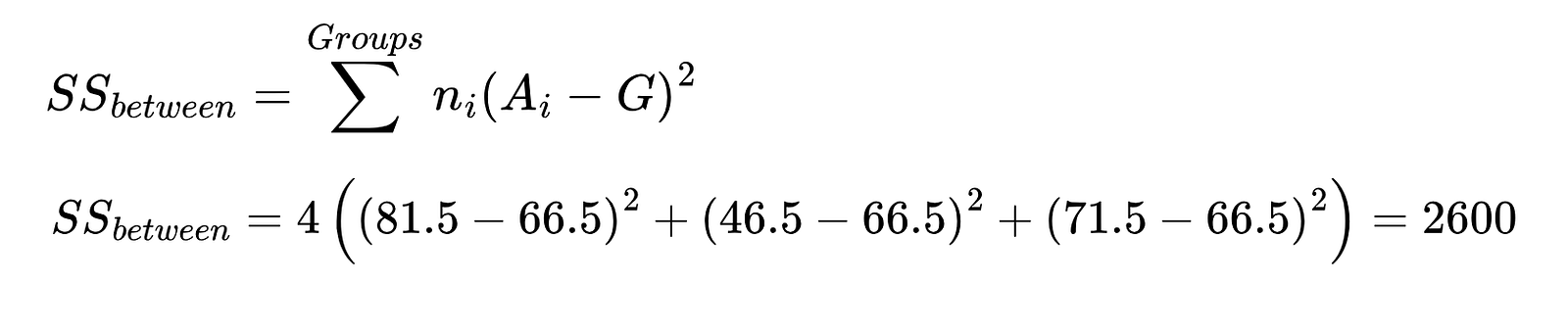Soma dos quadrados entre o grupo

Em seguida, calcule a soma dos quadrados dentro do grupo. É a soma da soma dos quadrados (SS) de cada grupo.

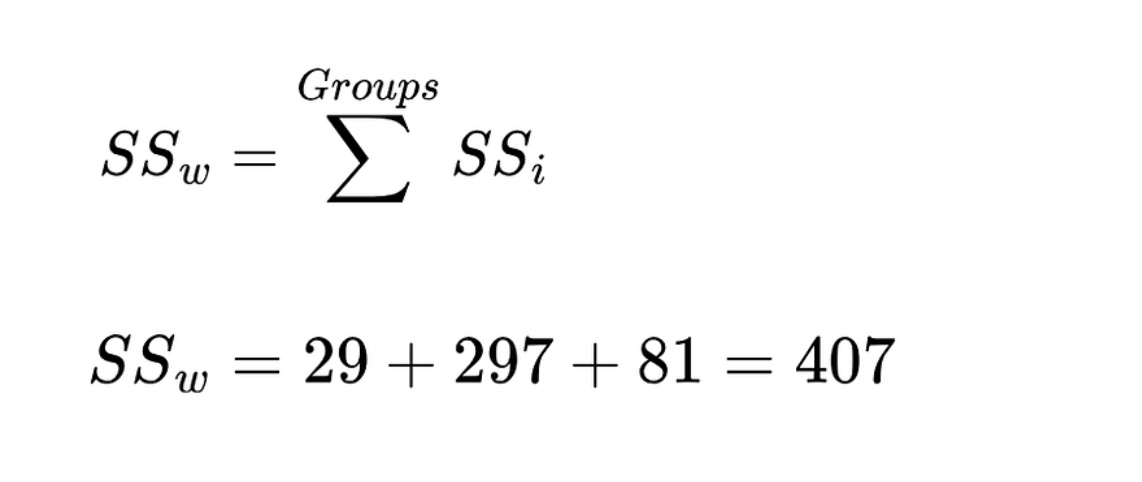
Soma dos quadrados dentro do grupo. Imagem do autor

Use a equação abaixo para calcular a soma total de quadrados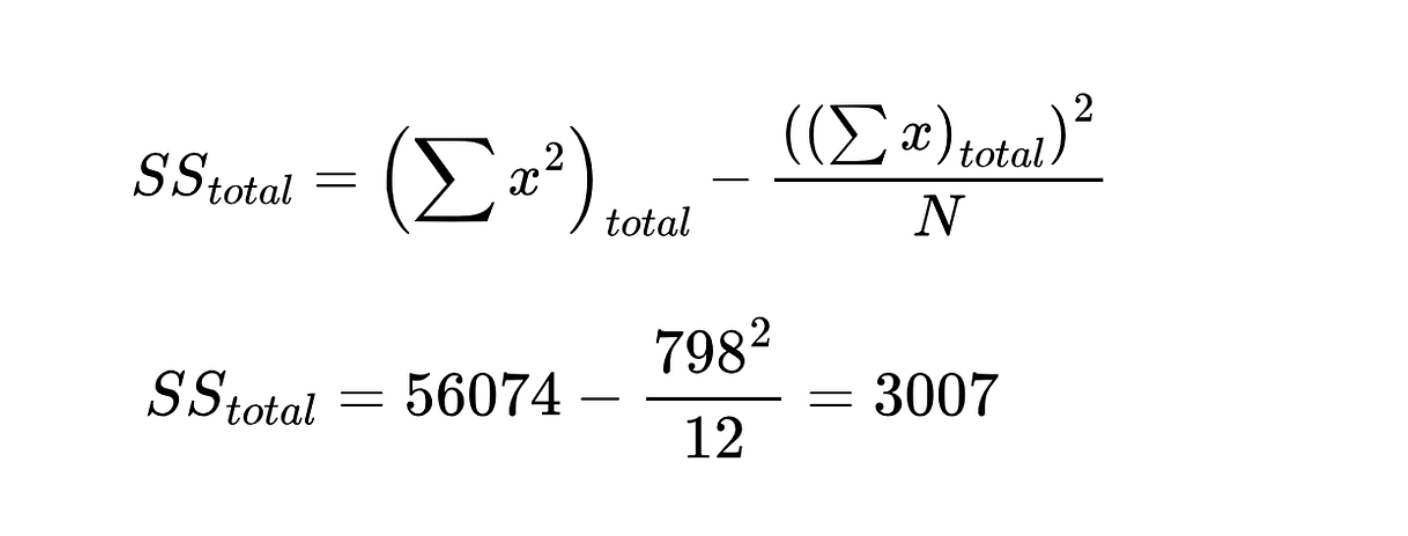
Soma total de quadrados. Imagem do autor

Verifique o cálculo verificando se a soma total dos quadrados é a adição da soma dos quadrados entre os grupos e a soma dos quadrados dentro do grupo. Depois de verificar, passe para o cálculo dos quadrados médios.

4. Calcule os quadrados médios

Os quadrados médios são a razão entre as somas quadradas e o grau de liberdade.

O grau de liberdade entre os grupos df_between é igual ao número de grupos menos um, e o grau de liberdade dentro dos grupos df_w é igual ao número total de participantes menos o número de grupos.

Com os valores calculados na etapa anterior, calcule os quadrados médios.

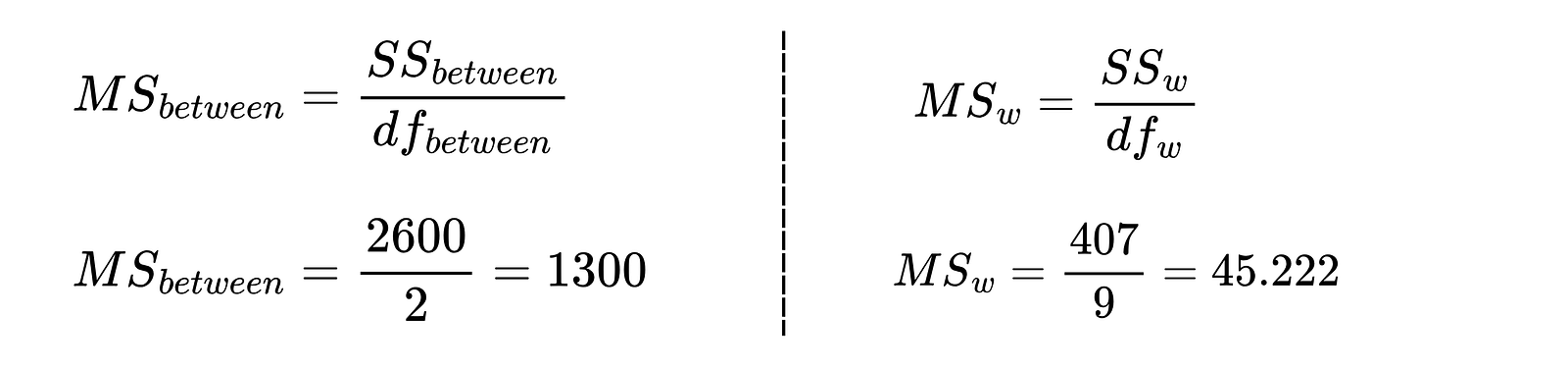Quadrados médios entre os grupos e dentro dos grupos. Imagem do autor

5. Calcule a estatística F usando a equação abaixo

A estatística F é a proporção do quadrado médio entre o grupo e o quadrado médio dentro do grupo.

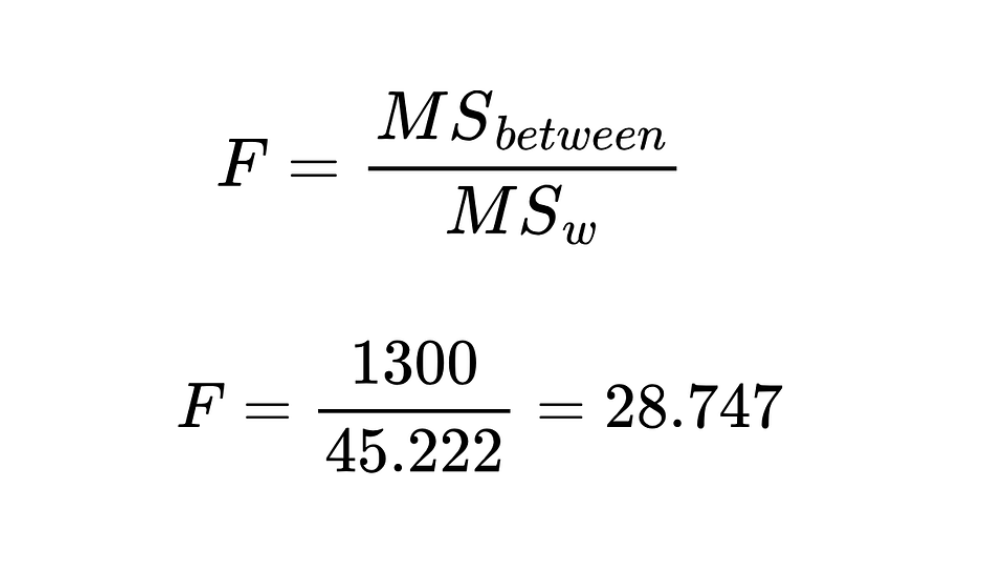
Estatística F. Imagem do autor

O valor calculado da estatística F é 28,747.

Por fim, o valor p é calculado usando a estatística F, o grau de liberdade df e a tabela de distribuição F.

Neste exemplo, o numerador df é 2, o denominador df é 9 e a estatística F é 28,747. Portanto, o valor p da tabela de distribuição F é 0,000123.

Etapa 4: Interpretar os resultados

• Estatística F: A estatística F mede a proporção da variação entre grupos em relação à variação dentro do grupo. Uma estatística F mais alta indica uma diferença mais significativa entre as médias do grupo em relação à variação aleatória.
• Valor de p: O valor de p determina se as diferenças entre as médias dos grupos são estatisticamente significativas. Se o valor de p estiver abaixo de um limite predefinido (geralmente 0,05), rejeite a hipótese nula e conclua que pelo menos um grupo tem uma média significativamente diferente.

O valor de p é 0,000123, e rejeitaríamos a hipótese nula para concluir que o método de ensino afeta significativamente as pontuações dos exames.

Testes Post-Hoc após ANOVA

A ANOVA nos informa se há uma diferença estatisticamente significativa entre as médias dos grupos, mas não especifica quais grupos são significativamente diferentes uns dos outros. Essa é a função dos testes post-hoc: eles realizam comparações de pares entre os grupos para identificar precisamente onde existem as diferenças. Quando você tem mais de dois grupos, esses testes são essenciais, e o resultado da ANOVA é significativo.

Continuando com nosso exemplo, o teste revela uma diferença significativa nas pontuações dos exames dos alunos após a realização da ANOVA unidirecional nos três métodos de ensino (Palestra, Workshop e Aprendizagem on-line). Um teste post-hoc nos ajudará a determinar quais métodos de ensino afetam de forma diferente o desempenho nos exames.

A diferença honestamente significativa (HSD) de Tukey e a correção de Bonferroni são testes post-hoc amplamente usados.

Alternativas à ANOVA

Se as premissas da ANOVA não forem atendidas, ou se a ANOVA não for adequada para o conjunto de dados, considere as seguintes alternativas.

1. Teste de Kruskal-Wallis: É uma alternativa não paramétrica à ANOVA unidirecional quando a suposição de normalidade é violada. É uma versão ampliada do teste U de Mann-Whitney.
2. MANOVA (Análise Multivariada de Variância): Ele estende os princípios da ANOVA a múltiplas variáveis dependentes. Ele testa se os vetores médios de várias variáveis dependentes diferem entre os grupos.

Conclusão

Este artigo apresentou os principais conceitos da ANOVA e destacou quando você deve usá-la em comparação com o teste t. Aprendemos que a ANOVA é uma análise estatística robusta que compara vários grupos simultaneamente. Fornecemos um guia passo a passo para a realização da ANOVA, detalhando como formular hipóteses, verificar suposições e interpretar resultados.

Para que você tenha experiência prática com o uso da ANOVA no Excel, confira o tutorial Guia completo de uso da ANOVA no Excel. Considere fazer os cursos Foundations of Inference in Python e Inferential Statistics para ampliar seus conhecimentos de estatística.