Cómo calcular la desviación típica en Excel

La desviación típica nos indica la dispersión de las cifras en un conjunto de datos determinado. Varios conceptos y métodos estadísticos importantes, como la varianza, el coeficiente de variación y los intervalos de confianza, dependen de la desviación típica como medida fundamental de la variabilidad, lo que la convierte en una de las herramientas estadísticas más importantes que deben dominar los profesionales de los datos.

Este artículo te introducirá en la desviación típica, te guiará en el cálculo de la desviación típica en Excel, te explicará las diferencias entre las funciones incorporadas disponibles y te demostrará cómo interpretar los resultados para tomar decisiones fundamentadas basadas en tu análisis. Si, al leer este artículo, descubres que te interesa la estadística de forma más general, sigue nuestro curso de Introducción a la Estadística, que cubre muchos temas fundamentales sin necesidad de codificación.

La respuesta rápida: Cómo calcular la desviación típica en Excel

Para calcular la desviación típica en Excel, introduce tus datos en una columna y, a continuación, utiliza la función STDEV.P() para una población o la funciónSTDEV.S() para una muestra. La principal diferencia entre estas funciones es que STDEV.P() divide por el número total de puntos de datos, mientras que STDEV.S() divide por el número de puntos de datos menos uno (n-1) para tener en cuenta la variabilidad de la muestra .

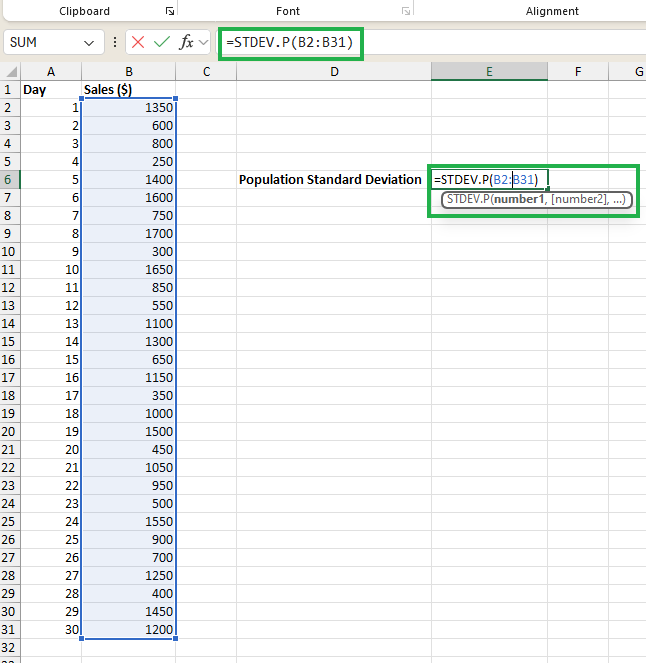
Cálculo rápido de la desviación típica en Excel. Imagen del autor.

Por ejemplo, si tus datos están en las celdas B2 a B31, escribe =STDEV.P(B2:B31) para calcular la desviación típica poblacional o =STDEV.S(B2:B31) para la desviación típica muestral. Excel calculará y mostrará automáticamente la desviación típica de tu conjunto de datos.

¿Qué es la desviación típica?

La desviación típica es una medida estadística que cuantifica la cantidad de variación o dispersión en un conjunto de valores numéricos. Indica cuánto se desvían los valores de un conjunto de datos de la media (promedio) del conjunto de datos. 

Ayuda a comprender el grado de variabilidad de los datos: una desviación típica baja indica que los valores están próximos a la media, lo que sugiere coherencia, mientras que una desviación típica alta indica una mayor variabilidad, lo que sugiere datos más dispersos.

Fórmulas para la desviación típica

La fórmula de la desviación típica depende de si se trata de una población o de una muestra. La fórmula de la desviación típica poblacional (σ) es la siguiente:

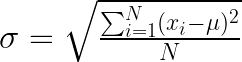
Desviación típica de la población. Imagen del autor.

Dónde:

• N es el número total de puntos de datos de la población.

• x_i​ representa cada punto de datos individual.

• μ es la media (promedio) de la población.

Esta fórmula calcula la media de las desviaciones al cuadrado de la media y luego saca la raíz cuadrada de esta media.

La fórmula de la desviación típica de la muestra (s) es la siguiente. Ten en cuenta que para la desviación típica muestral, utilizamos una n minúscula por convención.

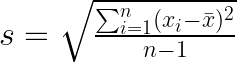
Ecuación de la desviación típica de la muestra. Imagen del autor.

Dónde:

• n es el número total de puntos de datos de la muestra.

• x_i​ representa cada punto de datos individual.

• xˉ es la media (promedio) de la muestra.

La fórmula es similar a la de la desviación típica de la población. Aún así, utiliza n - 1 (corrección de Bessel) en el denominador para tener en cuenta el hecho de que se está utilizando una muestra para estimar el parámetro poblacional. Esta corrección hace que la desviación típica de la muestra sea un estimador insesgado de la desviación típica de la población.​

Aplicaciones prácticas de la desviación típica

La desviación típica es una técnica muy utilizada en todos los campos. Proporciona información valiosa sobre la variabilidad y la coherencia de los datos y puede aplicarse a distintos ámbitos, como:

• Evaluación de riesgos: La desviación típica puede medir la volatilidad de los rendimientos de los activos. Una desviación típica más alta indica mayor riesgo y variabilidad potencial del rendimiento. Los inversores utilizan la desviación típica para comparar los niveles de riesgo de distintas inversiones y construir carteras diversificadas que equilibren riesgo y rentabilidad.
• Control de calidad: Las industrias de fabricación y producción utilizan la desviación típica para supervisar y controlar la calidad de los productos y procesos. Midiendo la variación de las dimensiones, el peso u otros atributos del producto, las empresas pueden garantizar la coherencia y el cumplimiento de las normas de calidad.
• Sanidad y Medicina: La desviación típica se utiliza en diversos análisis estadísticos para comprender la dispersión de los datos, como la tensión arterial de los pacientes, los niveles de colesterol y otros indicadores de salud. Ayuda a identificar los valores atípicos y a comprender el rango normal de las métricas de salud.
• Educación e Investigación: La desviación típica ayuda a determinar la distribución de las puntuaciones de los exámenes y establece curvas de calificación adecuadas. Los investigadores utilizan la desviación típica para estudiar la eficacia de las intervenciones educativas y comparar el rendimiento de distintos grupos de alumnos.
• Estudios meteorológicos y climáticos: Los meteorólogos utilizan la desviación típica para analizar los datos meteorológicos, como la temperatura, las precipitaciones y la velocidad del viento. Esto les ayuda a comprender la variabilidad del clima y a predecir los patrones meteorológicos.

Estos ejemplos pueden continuar, ya que la desviación típica es fundamental en estadística y análisis de datos, y puede extenderse a otros ámbitos más allá de los ejemplos anteriores.

Tipos de desviación típica

Al igual que las definiciones, Microsoft Excel tiene dos funciones diferentes para calcular la desviación típica, dependiendo de si trabajas con toda una población o con una muestra. 

STDEV.P() para la desviación típica de la población

La funciónSTDEV.P() de Excel calcula la desviación típica de toda una población. Esta función supone que los argumentos proporcionados incluyen a toda la población. La sintaxis de la función STDEV.P() es la siguiente:

STDEV.P(number1, [number2], ...)

Los parámetros son:

• number1: El primer argumento numérico corresponde a una población.

• [number2], ...: Números o referencias adicionales opcionales que corresponden a una población, hasta 254 argumentos.

STDEV.P() calcula la desviación típica utilizando la fórmula de la desviación típica de la población que aprendimos antes. Esto garantiza que el cálculo refleje las características de toda la población.

Debemos utilizar STDEV.P() cuando tengamos datos que representen a toda la población. Por ejemplo, cuando se analizan los resultados de los exámenes de todos los alumnos de un centro concreto, STDEV.P() es adecuado porque el conjunto de datos incluye a toda la población de interés.

STDEV.S() para la desviación típica de la muestra

La funciónSTDEV.S() de Excel calcula la desviación típica de una muestra de la población. Esta función supone que los argumentos proporcionados son una muestra de la población, no toda la población. La sintaxis de la función STDEV.S() es la siguiente:

STDEV.S(number1, [number2], ...)

Los parámetros son:

• number1: El primer argumento numérico corresponde a una muestra de la población.

• [number2], ...: Números o referencias adicionales opcionales que corresponden a una muestra, hasta 254 argumentos.

STDEV.S() calcula la desviación típica utilizando la fórmula de la desviación típica muestral, teniendo en cuenta la corrección de Bessel, como hemos aprendido antes.

En la práctica, cuando tenemos una muestra de datos, utilizamos STDEV.S() para estimar la desviación típica de toda la población. Supongamos que analizamos los resultados de los exámenes de un subconjunto de alumnos seleccionados al azar de un centro escolar. STDEV.S() es adecuado porque nuestro conjunto de datos es sólo una muestra de la población total de alumnos.

Ahora que ya conocemos las funciones disponibles en Excel para calcular la desviación típica, vamos a poner en práctica todos nuestros conocimientos mediante un ejemplo.

Calcular la desviación típica en Excel 

Imagina un escenario en el que, como analista de datos, se te pide que analices el rendimiento de las ventas de una pequeña tienda minorista. El propietario de la tienda quiere conocer la variabilidad de las ventas diarias durante el último mes para gestionar mejor el inventario y los niveles de personal. 

Has recogido los datos de ventas diarias durante 30 días y debes calcular la desviación típica para cuantificar esta variabilidad. 

Empecemos tabulando los registros de una columna, digamos B2 a B31, en una hoja de cálculo Excel.

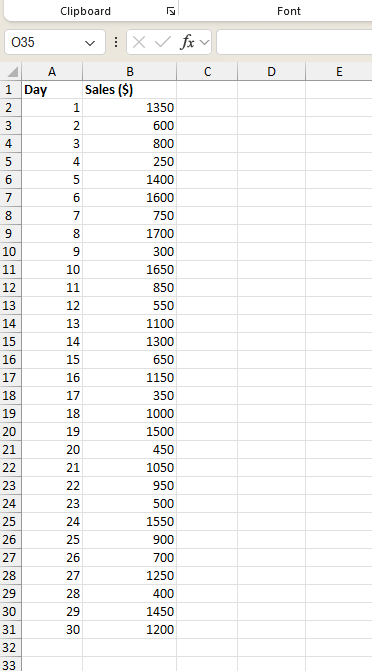
Almacena el conjunto de datos de ventas. Imagen del autor.

Podemos calcular la desviación típica de la población en la celda E6 escribiendo la siguiente ecuación:

=STDEV.P(B2:B31)

Verás la desviación típica poblacional calculada en la celda E6 de la siguiente manera:

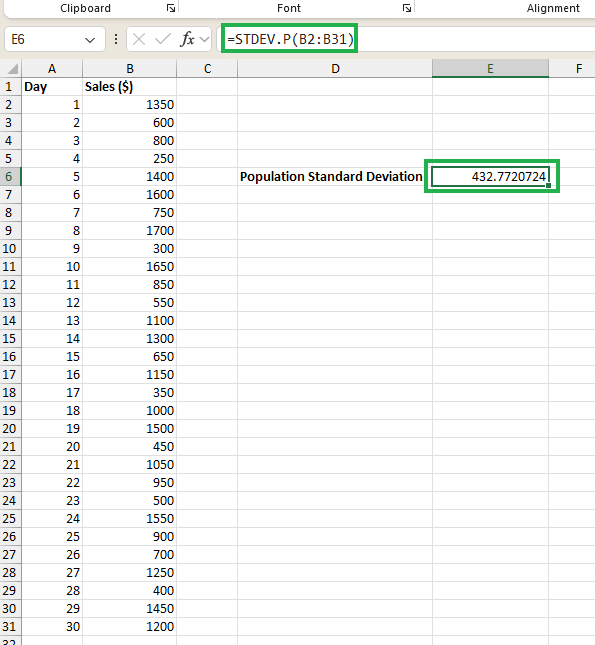
Calcular la desviación típica de la población. Imagen del autor.

Utilizamos la función STDEV.P() porque, en nuestro escenario, toda nuestra población para el análisis son los datos de ventas del último mes.

Supongamos que vamos a realizar un análisis para todo un año utilizando como muestra los datos de los últimos 30 días; entonces utilizaremos la función STDEV.S() como se muestra en la ecuación siguiente:

=STDEV.S(B2:B31)

Y a continuación veremos la desviación típica muestral calculada:

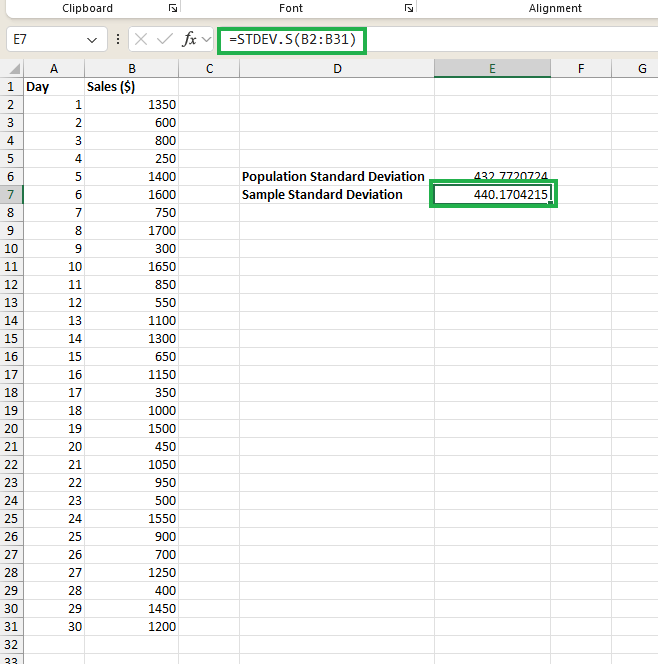
Cálculo de la desviación típica de la muestra. Imagen del autor.

Tras calcular la desviación típica, el siguiente paso es interpretar el resultado en un contexto empresarial. 

Interpretar los valores de la desviación típica

Para interpretar mejor los valores de la desviación típica y complementar nuestro análisis, podemos calcular el valor medio de nuestros datos de ventas mediante la siguiente ecuación:

=AVERAGE(B2:B31)

El valor medio puede calcularse como $975 en la celda E7, como se ve a continuación:

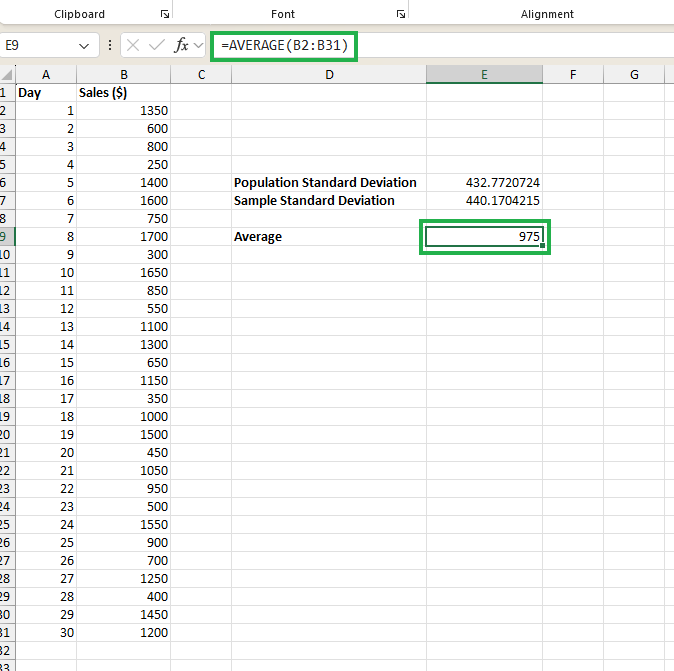
Calcular la media del conjunto de datos. Imagen del autor.

Junto con el valor medio obtenido, podemos interpretar los valores de la desviación típica como:

• Desviación típica de la población: La desviación típica de la población de aproximadamente 432,77 indica que, por término medio, las ventas diarias varían en unos 432,77 $ respecto al valor medio de ventas de 975 $. Esta cifra representa la dispersión de los datos de ventas, ya que consideramos todo el mes como un conjunto de datos completo.
• Desviación típica de la muestra: La desviación típica de la muestra, de aproximadamente 440,17, es ligeramente superior a la desviación típica de la población. Este valor es relevante si estamos tratando los datos de 30 días como una muestra de una población mayor (por ejemplo, todos los meses futuros posibles).
• Desviación típica de la muestra superior: El valor ligeramente superior de la desviación típica de la muestra explica la incertidumbre de utilizar una muestra para estimar la variabilidad global de las ventas. Sugiere que si tomamos una muestra de otro mes, podríamos esperar una variabilidad similar en las ventas diarias.
• Alta variabilidad en las ventas: Ambos valores de desviación típica indican una gran variabilidad en las ventas diarias, lo que significa que las cifras de ventas tienden a fluctuar significativamente respecto a la media de 975 $. Este nivel de variabilidad podría afectar a la gestión del inventario y a la dotación de personal. Algunos días, las ventas pueden ser muy superiores o inferiores a la media, lo que puede provocar un exceso o una falta de existencias si no se gestionan con cuidado.

Dado que los valores de la desviación típica sugieren que las ventas diarias son incoherentes y varían mucho, se puede realizar un análisis más detallado o construir un modelo de aprendizaje automático para estimar las ventas de un día concreto.

El propietario de la tienda debe tener en cuenta esta variabilidad al planificar el inventario y la dotación de personal para evitar posibles problemas relacionados con el exceso de existencias o la falta de personal.

Cómo añadir barras de desviación típica en Excel

Añadir barras de desviación típica a nuestros gráficos en Excel es una forma útil de representar visualmente la variabilidad de nuestros datos. 

Selecciona el rango de datos, B2 a B31, de nuestro ejemplo y ve a la opción Insertar Insertar. Elige el tipo de gráfico que desees, como se muestra en la imagen siguiente (por ejemplo, gráfico de líneas) e insértalo.

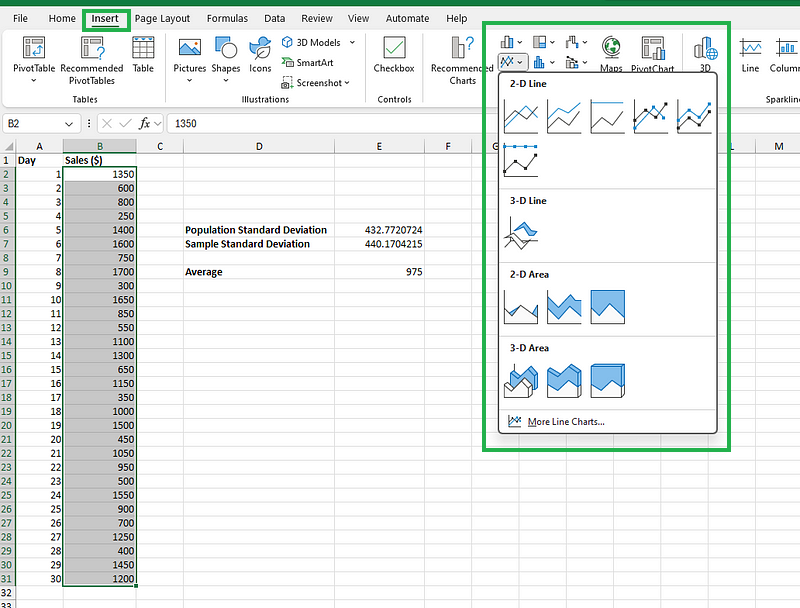
Insertar un gráfico para los datos de ventas de la tienda. Imagen del autor.

A continuación verás un sencillo gráfico de líneas:

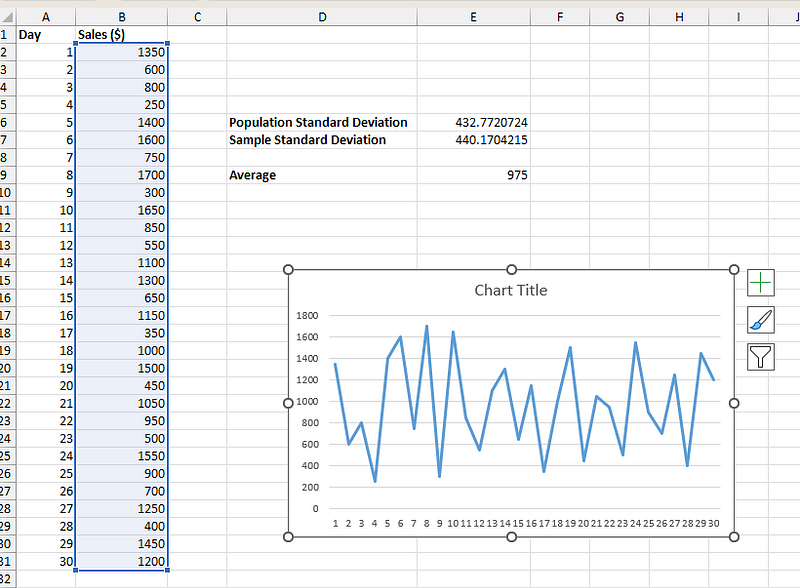
Gráfico de líneas para datos de ventas en tienda. Imagen del autor.

Haz clic en la serie de datos de tu gráfico para resaltarla. Este paso es necesario para añadir barras de error a la serie de datos seleccionada. Ir a la Gráfico Diseño que aparece cuando seleccionas el gráfico. Haz clic en Añadir Gráfico Elemento (que se encuentra en el grupo Diseños de Gráfico ).

A continuación, pasa el ratón por encima de Error Barras y selecciona Estándar Desviación Estándar para añadir las barras de desviación típica al gráfico de líneas.

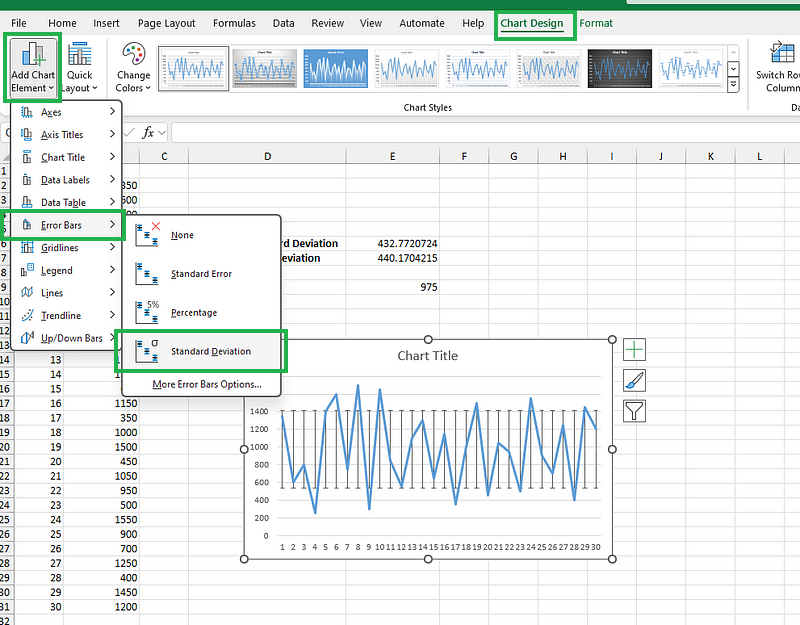
Añadir barras de desviación típica al gráfico de líneas. Imagen del autor.

También puedes pasar el ratón por encima Error Barras y luego hacer clic en Más Error Barras Opciones para dar más formato a las barras de error y ajustar el color, la anchura y el estilo de línea a las preferencias de diseño de tu gráfico. Esto se puede hacer en el mismo panel, en las opciones de Formato Barras Error. Siéntete libre de jugar con el gráfico hasta que consigas la trama que te gustaría visualizar.

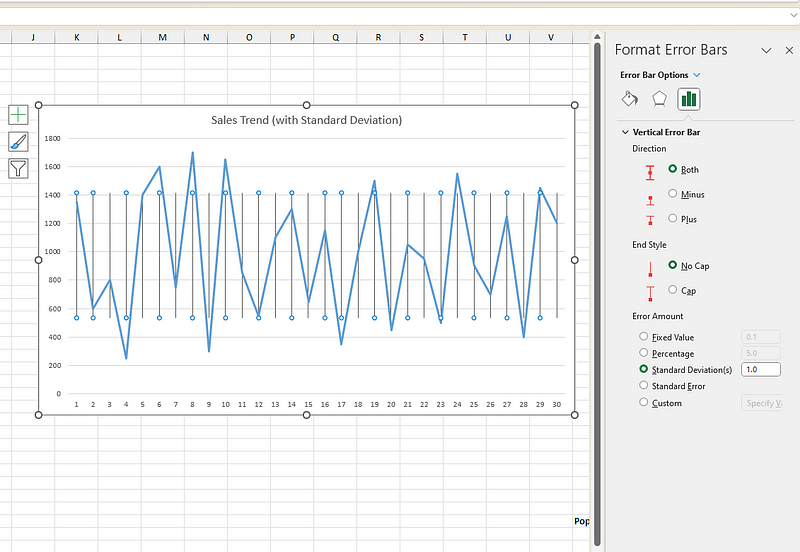
Formatear las barras de desviación típica. Imagen del autor.

Añadir barras de desviación típica a nuestros gráficos en Excel proporciona una representación visual clara de la variabilidad de los datos, lo que ayuda a un análisis eficaz de los datos y a la toma de decisiones.

Conclusión

Este artículo te ha presentado la desviación típica y sus aplicaciones prácticas. Establece los pasos para calcular la desviación típica en Excel. También aprendimos a interpretar los valores de la desviación típica y a añadir barras de desviación típica a un gráfico de líneas.

La desviación típica es una herramienta fundamental y valiosa que nos ayuda a comprender la variabilidad de un conjunto de datos. Además, se utiliza en otros muchos análisis, como el coeficiente de variación, los intervalos de confianza y el ANOVA, lo que la convierte en una técnica imprescindible para todos los profesionales de los datos.

Te animamos a que consultes nuestro completo curso práctico de Fundamentos de Excel para ampliar aún más tus conocimientos de Excel y de análisis de datos.