Curso
La clasificación es un proceso de dos pasos: un paso de aprendizaje y un paso de predicción. En la etapa de aprendizaje, el modelo se desarrolla basándose en los datos de entrenamiento proporcionados. En la etapa de predicción, el modelo se utiliza para predecir la respuesta a datos determinados. Un árbol de decisión es uno de los algoritmos de clasificación más sencillos y populares que se utilizan para comprender e interpretar datos. Se puede utilizar tanto para problemas de clasificación como de regresión.
Para ejecutar fácilmente todo el código de ejemplo de este tutorial, puedes crear un cuaderno de trabajo de DataLab de forma gratuita que tiene Python preinstalado y contiene todos los ejemplos de código. F
Conviértete en un Científico ML
El algoritmo del árbol de decisión
Un árbol de decisión es una estructura arbórea similar a un diagrama de flujo en la que un nodo interno representa una característica (o atributo), la rama representa una regla de decisión y cada nodo hoja representa el resultado.
El nodo superior de un árbol de decisión se conoce como nodo raíz. Aprende a dividir en particiones basándose en el valor del atributo. Divide el árbol de forma recursiva, lo que se denomina partición recursiva. Esta estructura similar a un diagrama de flujo te ayuda en la toma de decisiones. Es una visualización similar a un diagrama de flujo que imita fácilmente el pensamiento humano. Por eso los árboles de decisión son fáciles de entender e interpretar.
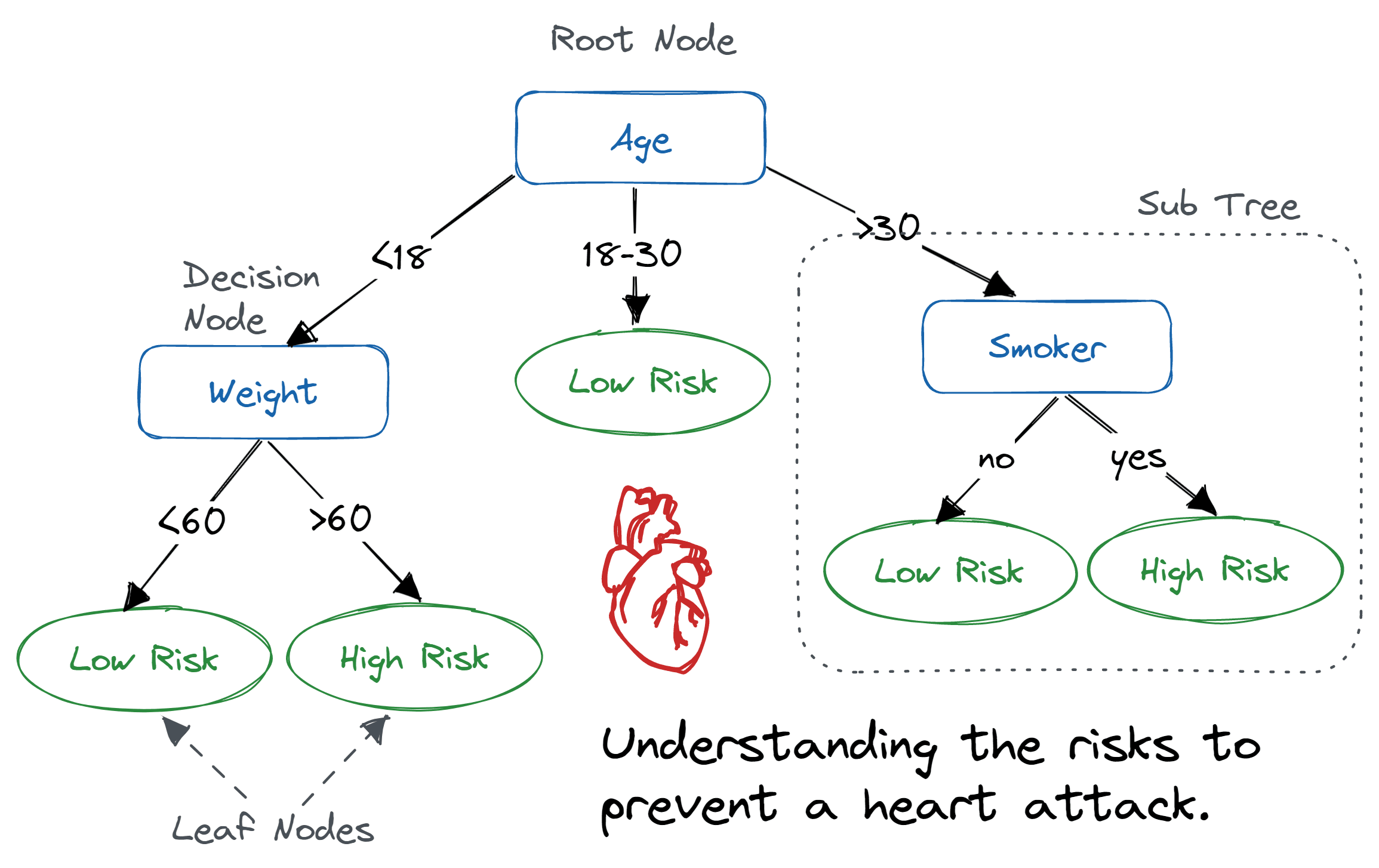
Algoritmo de árbol de decisión. Imagen de Abid Ali Awan.
Un árbol de decisión es un algoritmo de aprendizaje automático de tipo caja blanca. Comparte la lógica interna de toma de decisiones, que no está disponible en los algoritmos de tipo caja negra, como las redes neuronales. Tu tiempo de entrenamiento es más rápido en comparación con el algoritmo de red neuronal.
La complejidad temporal de los árboles de decisión es una función del número de registros y atributos de los datos proporcionados. El árbol de decisión es un método libre de distribución o no paramétrico que no depende de supuestos sobre la distribución de probabilidad subyacente de los datos. Los árboles de decisión pueden manejar datos de alta dimensión con buena precisión.
¿Cómo funciona el algoritmo del árbol de decisión?
La idea básica detrás de cualquier algoritmo de árbol de decisión es la siguiente:
- Selecciona el mejor atributo utilizando las medidas de selección de atributos (ASM) para dividir los registros.
- Convierte ese atributo en un nodo de decisión y divide el conjunto de datos en subconjuntos más pequeños.
- Comienza a construir el árbol repitiendo este proceso de forma recursiva para cada hijo hasta que se cumpla una de las condiciones:
- Todas las tuplas pertenecen al mismo valor de atributo.
- No quedan más atributos.
- No hay más instancias.
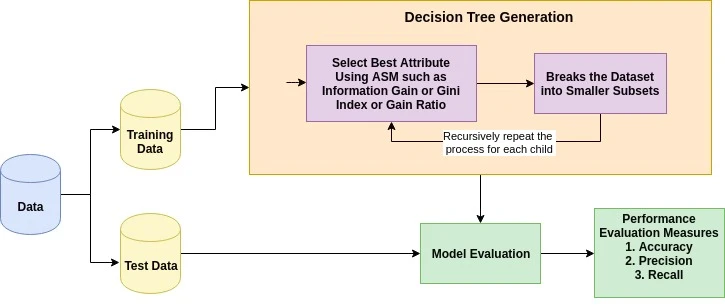
Medidas de selección de atributos
La medida de selección de atributos es una heurística para seleccionar el criterio de división que divide los datos de la mejor manera posible. También se conoce como reglas de división porque nos ayuda a determinar los puntos de ruptura para las tuplas en un nodo determinado. ASM asigna una clasificación a cada característica (o atributo) explicando el conjunto de datos dado. El atributo de mejor puntuación se seleccionará como atributo de división (Fuente). En el caso de un atributo de valor continuo, también es necesario definir puntos de división para las ramas. Las medidas de selección más populares son la ganancia de información, la relación de ganancia y el índice de Gini.
Ganancia de información
Claude Shannon inventó el concepto de entropía, que mide la impureza del conjunto de entrada. En física y matemáticas, la entropía se refiere a la aleatoriedad o la impureza en un sistema. En teoría de la información, se refiere a la impureza en un grupo de ejemplos. La ganancia de información es la disminución de la entropía. La ganancia de información calcula la diferencia entre la entropía antes de la división y la entropía media después de la división del conjunto de datos basándose en los valores de los atributos dados. El algoritmo del árbol de decisión ID3 (Iterative Dichotomiser) utiliza la ganancia de información.
Donde Pi es la probabilidad de que una tupla arbitraria en D pertenezca a la clase Ci.
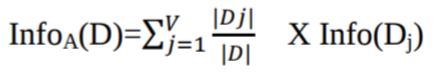
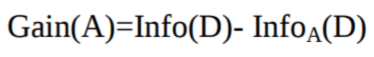
Dónde:
-
Info(D)es la cantidad media de información necesaria para identificar la etiqueta de clase de una tupla enD. -
|Dj|/|D|actúa como el peso de la particiónj. -
InfoA(D)es la información esperada necesaria para clasificar una tupla deDbasándose en la partición deA.
El atributo A con la mayor ganancia de información, Gain(A), se elige como atributo de división en el nodo N().
Relación de ganancia
La ganancia de información está sesgada hacia el atributo con muchos resultados. Significa que prefiere el atributo con un gran número de valores distintos. Por ejemplo, consideremos un atributo con un identificador único, como customer_ID, que tiene cero información (D) debido a una partición pura. Esto maximiza la ganancia de información y crea particiones inútiles.
C4.5, una mejora de ID3, utiliza una extensión de la ganancia de información conocida como ratio de ganancia. La relación de ganancia aborda el problema del sesgo normalizando la ganancia de información mediante Split Info. La implementación en Java del algoritmo C4.5 se conoce como J48, y está disponible en la herramienta de minería de datos WEKA.
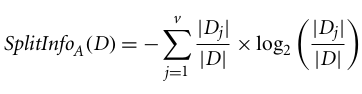
Dónde:
- |Dj|/|D| actúa como el peso de la partición j-ésima.
- v es el número de valores discretos en el atributo A.
La relación de ganancia se puede definir como
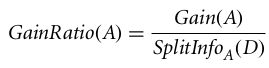
El atributo con la mayor relación de ganancia se elige como atributo de división (Fuente).
Índice de Gini
Otro algoritmo de árbol de decisión, CART (árbol de clasificación y regresión), utiliza el método de Gini para crear puntos de división.
Donde pi es la probabilidad de que una tupla en D pertenezca a la clase Ci.
El índice de Gini considera una división binaria para cada atributo. Puedes calcular una suma ponderada de la impureza de cada partición. Si una división binaria en el atributo A divide los datos D en D1 y D2, el índice de Gini de D es:
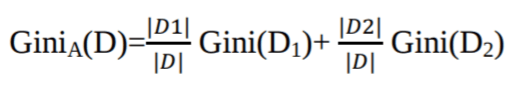
En el caso de un atributo con valores discretos, el subconjunto que da el índice de Gini mínimo para el elegido se selecciona como atributo de división. En el caso de los atributos de valor continuo, la estrategia consiste en seleccionar cada par de valores adyacentes como posible punto de división, y se elige como punto de división aquel que tenga un índice de Gini menor.
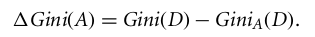
El atributo con el índice de Gini mínimo se elige como atributo de división.
Ejecuta y edita el código de este tutorial en línea
Ejecutar códigoCreación de clasificadores de árboles de decisión en Scikit-learn
Importación de las bibliotecas necesarias
Primero carguemos las bibliotecas necesarias.
# Load libraries
import pandas as pd
from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier
from sklearn.model_selection import train_test_split # Import train_test_split function
from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation
Cargando datos
Primero, carguemos el conjunto de datos necesario sobre la diabetes entre los indios pima utilizando la función CSV de lectura de pandas. Puedes descargar el conjunto de datos de Kaggle para seguir el ejemplo.
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
# load dataset
pima = pd.read_csv("diabetes.csv", header=None, names=col_names)
pima.head()
| embarazada | glucosa | bp | piel | insulina | bmi | pedigrí | edad | etiqueta | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23,3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0,167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43,1 | 2.288 | 33 | 1 |
Selección de características
Aquí, debes dividir las columnas dadas en dos tipos de variables: variables dependientes (o variables objetivo) y variables independientes (o variables características).
#split dataset in features and target variable
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable
División de datos
Para comprender el rendimiento del modelo, una buena estrategia consiste en dividir el conjunto de datos en un conjunto de entrenamiento y un conjunto de prueba.
Dividamos el conjunto de datos utilizando la función train_test_split(). Debes pasar tres parámetros: características, objetivo y tamaño del conjunto de pruebas.
# Split dataset into training set and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test
Creación de un modelo de árbol de decisión
Creemos un modelo de árbol de decisión utilizando Scikit-learn.
# Create Decision Tree classifer object
clf = DecisionTreeClassifier()
# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
Evaluación del modelo
Calculemos con qué precisión el clasificador o modelo puede predecir el tipo de cultivares.
La precisión se puede calcular comparando los valores reales del conjunto de pruebas y los valores previstos.
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.6753246753246753
Obtenemos una tasa de clasificación del 67,53 %, lo que se considera una buena precisión. Puedes mejorar esta precisión ajustando los parámetros del algoritmo del árbol de decisión.
Visualización de árboles de decisión
Puedes utilizar la función « export_graphviz() » de Scikit-learn para mostrar el árbol en un cuaderno Jupyter. Para gráficar el árbol, también es necesario instalar graphviz y pydotplus.
pip install graphviz
pip install pydotplusLa función export_graphviz() convierte el clasificador del árbol de decisión en un archivo dot, y pydotplus convierte este archivo dot en PNG o en un formato visualizable en Jupyter.
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())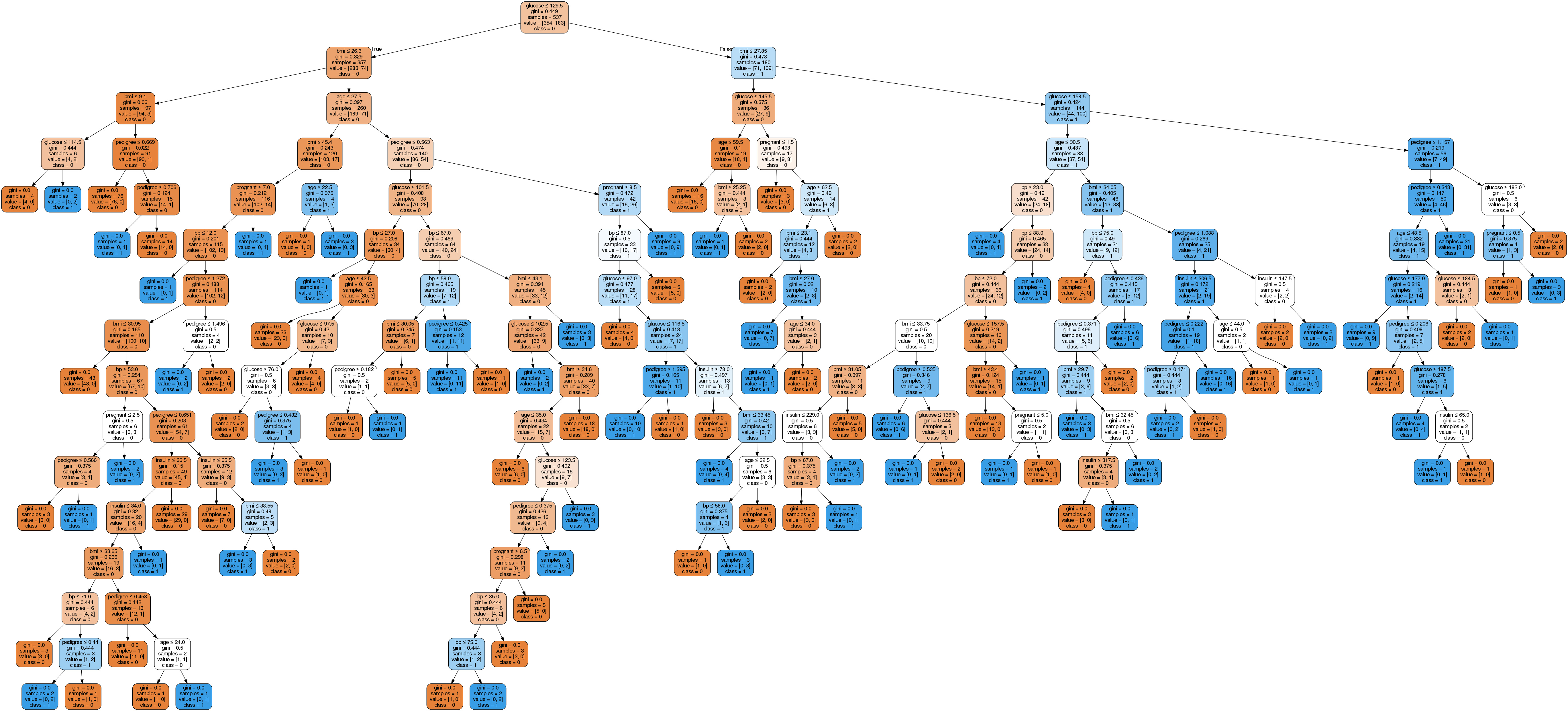
En el diagrama del árbol de decisión, cada nodo interno tiene una regla de decisión que divide los datos. El Gini, conocido como coeficiente de Gini, mide la impureza del nodo. Se puede decir que un nodo es puro cuando todos sus registros pertenecen a la misma clase; estos nodos se conocen como nodos hoja.
Aquí, el árbol resultante no está podado. Este árbol sin podar es inexplicable y difícil de entender. En la siguiente sección, vamos a optimizarlo mediante la poda.
Optimización del rendimiento del árbol de decisión
-
criterio: opcional (por defecto = «gini») o elegir medida de selección de atributos. Este parámetro nos permite utilizar la medida de selección de atributos diferente-diferente. Los criterios admitidos son «gini» para el índice de Gini y «entropía» para la ganancia de información.
-
divisor: cadena, opcional (por defecto = «best») o estrategia de división. Este parámetro nos permite elegir la estrategia de división. Las estrategias compatibles son «óptima», para elegir la mejor división, y «aleatoria», para elegir la mejor división aleatoria.
-
max_depth: int o None, opcional (por defecto=None) o profundidad máxima de un árbol. La profundidad máxima del árbol. Si None, los nodos se expanden hasta que todas las hojas contengan menos de min_samples_split muestras. Un valor más alto de profundidad máxima provoca un sobreajuste, y un valor más bajo provoca un subajuste (Fuente).
En Scikit-learn, la optimización del clasificador de árboles de decisión se realiza únicamente mediante la poda previa. La profundidad máxima del árbol se puede utilizar como variable de control para la poda previa. En el siguiente ejemplo, puedes crear un gráfico de un árbol de decisión con los mismos datos con max_depth=3. Además de los parámetros de pre-poda, también puedes probar otras medidas de selección de atributos, como la entropía.
# Create Decision Tree classifer object
clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)
#Predict the response for test dataset
y_pred = clf.predict(X_test)
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.7705627705627706Bueno, la tasa de clasificación aumentó al 77,05 %, lo que supone una mayor precisión que el modelo anterior.
Hagamos que tu árbol de decisión sea un poco más fácil de entender utilizando el siguiente código:
from six import StringIO
from IPython.display import Image
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True,
rounded=True,
special_characters=True,
feature_names=feature_cols,
class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('diabetes.png')
Image(graph.create_png())Aquí, hemos completado los siguientes pasos:
-
Importaste las bibliotecas necesarias.
-
Creaste un objeto
StringIOllamadodot_datapara almacenar la representación textual del árbol de decisión. -
Exporta el árbol de decisión al formato
dotutilizando la funciónexport_graphvizy escribe el resultado en el búferdot_data. -
Creó un objeto gráfico
pydotplusa partir de la representación en formatodotdel árbol de decisión almacenado en el búferdot_data. -
Escribe el gráfico generado en un archivo PNG llamado «diabetes.png».
-
Mostró la imagen PNG generada del árbol de decisión utilizando el objeto
Imagedel móduloIPython.display.
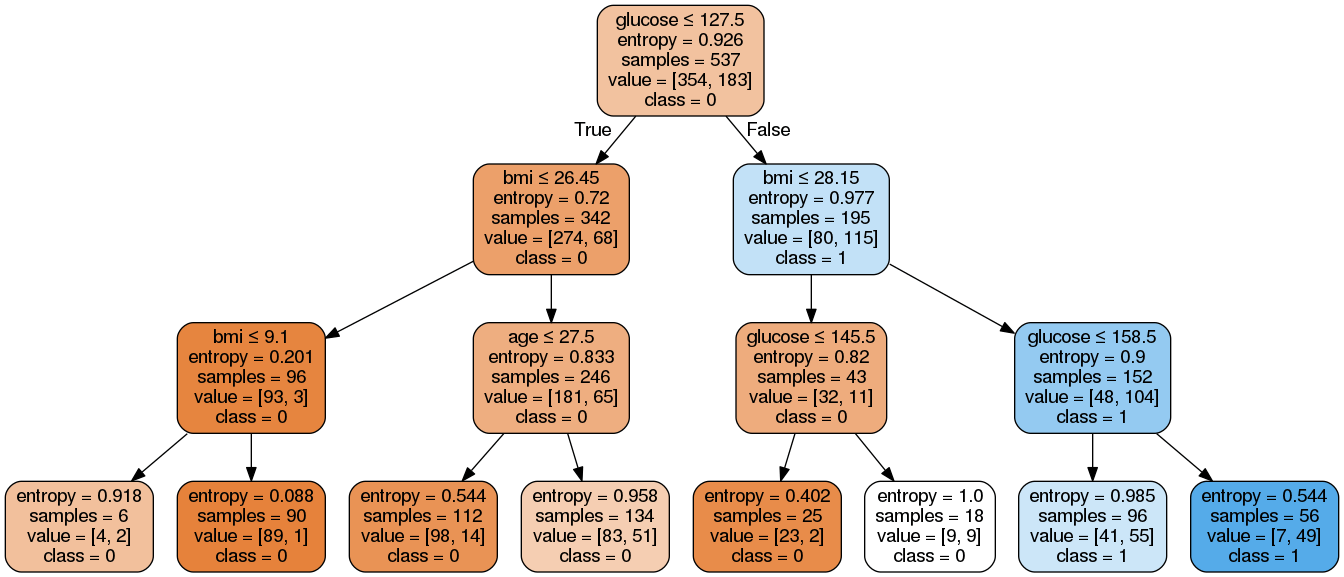
Como puedes ver, este modelo podado es menos complejo, más explicable y más fácil de entender que el anterior gráfico del modelo de árbol de decisión.
Ventajas y desventajas del árbol de decisión
Ahora que ya has creado y optimizado un clasificador de árbol de decisión, tomemos un momento para evaluar algunas de las fortalezas y limitaciones del algoritmo de manera más general. Comprender las ventajas y desventajas te ayuda a decidir cuándo los árboles de decisión son la opción adecuada.
| Ventajas | Desventajas |
|---|---|
| Fácil de interpretar y visualizar | Sensible a los datos ruidosos y puede sobreajustarse. |
| Puede capturar fácilmente patrones no lineales. | Pequeñas variaciones en los datos pueden dar lugar a árboles muy diferentes. |
| Requiere un preprocesamiento mínimo de los datos (no es necesario normalizar las columnas). | Sesgado con conjuntos de datos desequilibrados (se recomienda equilibrarlos) |
| Útil para la ingeniería de características (predicción de valores perdidos, selección de variables). | |
| Sin supuestos sobre la distribución de datos (no paramétrico) |
Ten en cuenta que algunas desventajas, como la inestabilidad de la varianza, pueden mitigarse mediante métodos de conjunto, como los algoritmosde baggingyboosting.
Árbol de decisión frente a Tronco de decisión
Aunque a lo largo de este tutorial hemos estado trabajando con árboles de decisión completos, vale la pena comprender una variante más simple llamada «tronco de decisión». Un tronco de decisión es esencialmente un árbol de decisión con una profundidad máxima de uno, lo que significa que solo tiene una división en el nodo raíz y dos nodos hoja.
| Aspecto | Árbol de decisión | Tronco de decisión |
|---|---|---|
| Profundidad | Puede ser de cualquier profundidad (controlada por max_depth parámetro) |
Siempre profundidad 1 (una sola división) |
| Complejidad | Puede modelar relaciones complejas y no lineales. | Modelos solo con límites de decisión simples y lineales. |
| Caso de uso | Clasificador independiente para problemas complejos | Utilizado principalmente como un alumno débil en métodos conjuntos. |
| Precisión | Generalmente mayor precisión como modelo independiente. | Menor precisión, pero eficaz cuando se combina |
| Interpretabilidad | Disminuye con la profundidad (como vimos con nuestro árbol sin podar). | Extremadamente sencillo e interpretable. |
Los árboles de decisión rara vez se utilizan como clasificadores independientes debido a su simplicidad. Sin embargo, pueden desempeñar un papel importante en los métodos de conjunto, en particular AdaBoost utiliza los stumps de decisión como aprendices débiles que se combinan para crear un clasificador fuerte, oel gradiente boosting, ya que los stumps pueden utilizarse como aprendices base en el proceso de boosting.
Puedes crear un árbol de decisión en Scikit-learn simplemente configurando un max_depth=1:
# Create a Decision Stump
stump = DecisionTreeClassifier(max_depth=1)
stump = stump.fit(X_train, y_train)Conclusión
¡Enhorabuena, has llegado al final de este tutorial!
En este tutorial, has aprendido muchos detalles sobre los árboles de decisión: cómo funcionan, medidas de selección de atributos como la ganancia de información, la relación de ganancia y el índice de Gini, la creación de modelos de árboles de decisión, la visualización y la evaluación de un conjunto de datos sobre diabetes utilizando el paquete Scikit-learn de Python. También analizamos sus ventajas, desventajas y cómo optimizar el rendimiento del árbol de decisión mediante el ajuste de parámetros.
Con suerte, ahora podrás utilizar el algoritmo del árbol de decisión para analizar tus propios conjuntos de datos.
Si deseas obtener más información sobre el machine learning en Python, realiza nuestro curso Machine learning con modelos basados en árboles en Python. Además, échale un vistazo a nuestro tutorial de Kaggle « » (Eliminar datos duplicados): Tu primer modelo de machine learning.
Certifícate en el puesto de Científico de Datos de tus sueños
Nuestros programas de certificación te ayudan a destacar y a demostrar que tus aptitudes están preparadas para el trabajo a posibles empleadores.
Preguntas frecuentes sobre la clasificación mediante árboles de decisión
¿Cuáles son los casos de uso más comunes para la clasificación mediante árboles de decisión?
La clasificación mediante árboles de decisión se utiliza habitualmente en diversos campos, como las finanzas para la puntuación crediticia, la sanidad para el diagnóstico de enfermedades, el marketing para la segmentación de clientes, etc. Ayuda a tomar decisiones dividiendo los datos en subconjuntos según diferentes criterios.
¿Cómo puedes evitar el sobreajuste cuando utilizas árboles de decisión?
El sobreajuste se puede evitar podando el árbol, estableciendo una profundidad máxima, utilizando un número mínimo de muestras necesarias para dividir un nodo interno y utilizando un número mínimo de muestras necesarias para estar en un nodo hoja. La validación cruzada también puede ayudar a ajustar estos parámetros de manera eficaz.
¿Cuál es la diferencia entre un árbol de decisión y un bosque aleatorio?
Un árbol de decisión es una estructura de árbol único que se utiliza para la clasificación o la regresión. Por otro lado, un bosque aleatorio es un conjunto de múltiples árboles de decisión que mejora la precisión predictiva y controla el sobreajuste mediante el promedio de los resultados de varios árboles.
¿Cómo gestionas los valores perdidos en tu conjunto de datos cuando utilizas árboles de decisión?
Los árboles de decisión pueden manejar valores faltantes utilizando divisiones sustitutivas o sustituyendo los valores faltantes por el valor más frecuente o la media/moda de la característica. Scikit-learn también proporciona métodos como SimpleImputer para rellenar los valores que faltan antes de entrenar el modelo.
¿Cuáles son las ventajas de utilizar Scikit-learn para crear modelos de árboles de decisión?
Scikit-learn proporciona una herramienta sencilla y eficaz para la minería y el análisis de datos, incluidos los clasificadores de árboles de decisión. Ofrece diversas características, como fácil integración, amplia documentación, compatibilidad con diversas métricas y ajuste de parámetros, y métodos para visualizar árboles de decisión, lo que lo convierte en una opción muy popular entre los profesionales del machine learning.
