Programación lineal: Resolución de problemas de optimización del mundo real

Los directores de operaciones se enfrentan a un reto recurrente: demasiadas decisiones, demasiadas limitaciones y ninguna forma clara de encontrar la mejor solución. Una red de distribución debe minimizar los costes de combustible en docenas de rutas, respetando al mismo tiempo los plazos de entrega, la capacidad de los vehículos y los horarios de los conductores.

Estos dos problemas comparten una estructura matemática. Cuando tus objetivos y restricciones pueden expresarse como relaciones lineales, estás trabajando con un problema de programación lineal. Nos interesa la programación lineal porque encuentra soluciones óptimas cuando se trabaja con recursos limitados y requisitos contrapuestos.

Lo que hace que la programación lineal sea tan potente es su garantía: si existe una solución viable, el algoritmo encontrará la óptima. Por supuesto, las aplicaciones del mundo real rara vez se ajustan perfectamente a los ejemplos de los libros de texto, pero comprender el marco básico te ayuda a reconocer cuándo la optimización puede sustituir a las conjeturas.

Esta guía te lleva desde los fundamentos hasta las implementaciones prácticas de Python. Avanzaremos desde problemas sencillos con dos variables que se pueden visualizar geométricamente hasta escenarios complejos que requieren soluciones algorítmicas. Comprenderás tanto la teoría matemática que hace posible la optimización como las habilidades prácticas para implementar soluciones por ti mismo.

¿Qué es la programación lineal?

La programación lineal optimiza una función objetivo lineal sujeta a restricciones lineales. En un proyecto de distribución de rutas en el que trabajé, el objetivo era minimizar la distancia total recorrida respetando restricciones como la capacidad de los vehículos y los plazos de entrega.

Comprender la estructura básica

Todo problema de programación lineal tiene tres componentes: variables de decisión, una función objetivo y restricciones.

Las variables de decisión representan las elecciones que estás tomando. En los problemas de rutas, las variables binarias pueden indicar qué vehículo visita cada ubicación. En la planificación de la producción, las variables pueden representar cantidades de fabricación.

La función objetivo define lo que estás optimizando. Debe ser una combinación lineal de tus variables de decisión. Las restricciones definen las reglas y limitaciones de tu problema. Tienen tres formas: igualdades, desigualdades menores o iguales, o mayores o iguales.

from scipy.optimize import linprog

c = [10, 15]
A_ub = [[1, 0], [0, 1]]
b_ub = [100, 80]
A_eq = [[1, 1]]
b_eq = [150]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, 
                 bounds=bounds, method='highs')

print(f"Optimal solution: Truck 1 = {result.x[0]:.1f}, Truck 2 = {result.x[1]:.1f}")
print(f"Total cost: ${result.fun:.2f}")

El código anterior minimiza el costo total para dos variables de decisión, sujeto a límites individuales y un requisito de cobertura total. Los coeficientes objetivos [10, 15] representan el coste por unidad, las restricciones de desigualdad limitan el rango de cada variable y la restricción de igualdad garantiza la cobertura total.

Interpretación geométrica

Comprender la programación lineal desde un punto de vista geométrico transformó mi forma de pensar sobre la optimización. Cada restricción define un semiespacio, y su intersección forma la región factible. Esta región es e e siempre un politopo convexo, lo que significa que cualquier línea entre dos puntos interiorespermanece dentro.

Aquí está la idea clave: las soluciones óptimas siempre se dan en los vértices de la región factible. Avanzar por un borde mejora tu objetivo o no, por lo que sigues avanzando hasta llegar a una esquina. Esta propiedad hace que los algoritmos de programación lineal sean eficientes.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 8, 400)
y1 = (10 - x) / 2
y2 = 12 - 2*x

plt.figure(figsize=(10, 8))
plt.plot(x, y1, 'r-', label='x + 2y ≤ 10', linewidth=2)
plt.plot(x, y2, 'b-', label='2x + y ≤ 12', linewidth=2)

y_feasible = np.minimum(y1, y2)
y_feasible = np.maximum(y_feasible, 0)
plt.fill_between(x, 0, y_feasible, where=(y_feasible >= 0), 
                 alpha=0.3, color='green', label='Feasible region')

vertices = [(0, 0), (0, 5), (14/3, 8/3), (6, 0)]
for v in vertices:
    plt.plot(v[0], v[1], 'ko', markersize=10)
    obj_value = 3*v[0] + 4*v[1]
    plt.annotate(f'({v[0]:.1f}, {v[1]:.1f})\nObj: {obj_value:.1f}',
                 xy=v, xytext=(v[0]+0.3, v[1]+0.3))

plt.xlim(-0.5, 8)
plt.ylim(-0.5, 8)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True, alpha=0.3)
plt.title('Geometric View: Optimal Solution at Vertex (4.7, 2.7)')
plt.show()

Esta visualización muestra la solución óptima en el vértice (4,7, 2,7), donde se cruzan dos restricciones. La región factible convexa garantiza que no haya valles ocultos en los que los algoritmos puedan atascarse, lo que asegura que los óptimos locales sean iguales a los óptimos globales.

Transformando problemas del mundo real

Lo más difícil no es resolver los problemas matemáticos, sino traducir problemas confusos en formulaciones claras. Definir variables y restricciones suele llevar más tiempo que ejecutar la optimización en sí.

Definir las variables de decisión requiere identificar las opciones fundamentales. Para el enrutamiento, puedes utilizar variables binarias para las asignaciones de ubicación de vehículos o añadir variables continuas para el orden de las visitas con el fin de simplificar las restricciones.

Construir restricciones significa traducir reglas de negocio en desigualdades. Esto revela suposiciones ocultas. Cuando un gerente dice «cada ubicación necesita una entrega», ¿significa eso exactamente una o al menos una? Estos detalles cambian completamente la formulación.

Aquí tienes un ejemplo de formulación utilizando PuLP:

from pulp import *

prob = LpProblem("Food_Bank_Routing", LpMinimize)

trucks = ['Truck_A', 'Truck_B', 'Truck_C']
centers = ['North', 'South', 'East', 'West', 'Central']

x = LpVariable.dicts("route", 
                     [(i, j) for i in trucks for j in centers],
                     cat='Binary')

distances = {
    ('Truck_A', 'North'): 15, ('Truck_A', 'South'): 20,
    ('Truck_A', 'East'): 10, ('Truck_A', 'West'): 25,
    ('Truck_A', 'Central'): 5,
    ('Truck_B', 'North'): 18, ('Truck_B', 'South'): 15,
    ('Truck_B', 'East'): 12, ('Truck_B', 'West'): 22,
    ('Truck_B', 'Central'): 8,
    ('Truck_C', 'North'): 20, ('Truck_C', 'South'): 25,
    ('Truck_C', 'East'): 15, ('Truck_C', 'West'): 18,
    ('Truck_C', 'Central'): 10,
}

prob += lpSum([distances[i, j] * x[i, j] 
               for i in trucks for j in centers])

for j in centers:
    prob += lpSum([x[i, j] for i in trucks]) == 1

max_stops = {'Truck_A': 3, 'Truck_B': 2, 'Truck_C': 3}
for i in trucks:
    prob += lpSum([x[i, j] for j in centers]) <= max_stops[i]

prob.solve()

print(f"Status: {LpStatus[prob.status]}")
print(f"Total distance: {value(prob.objective)} miles")
for i in trucks:
    route = [j for j in centers if value(x[i, j]) == 1]
    print(f"{i} visits: {', '.join(route)}")

La formulación anterior utiliza variables binarias para las asignaciones de camiones a centros, minimiza la distancia total, garantiza que cada centro reciba exactamente una entrega y respeta los límites de capacidad de los camiones.

Los patrones de problemas clásicos proporcionan plantillas. El problema de la dieta minimiza los costes y, al mismo tiempo, satisface las necesidades nutricionales. Los problemas de transporte minimizan los gastos de envío. Esto se aplicaba directamente a mi propio reto de enrutamiento. Reconocer estos patrones acelera la formulación, ya que rara vez se resuelven problemas realmente novedosos.

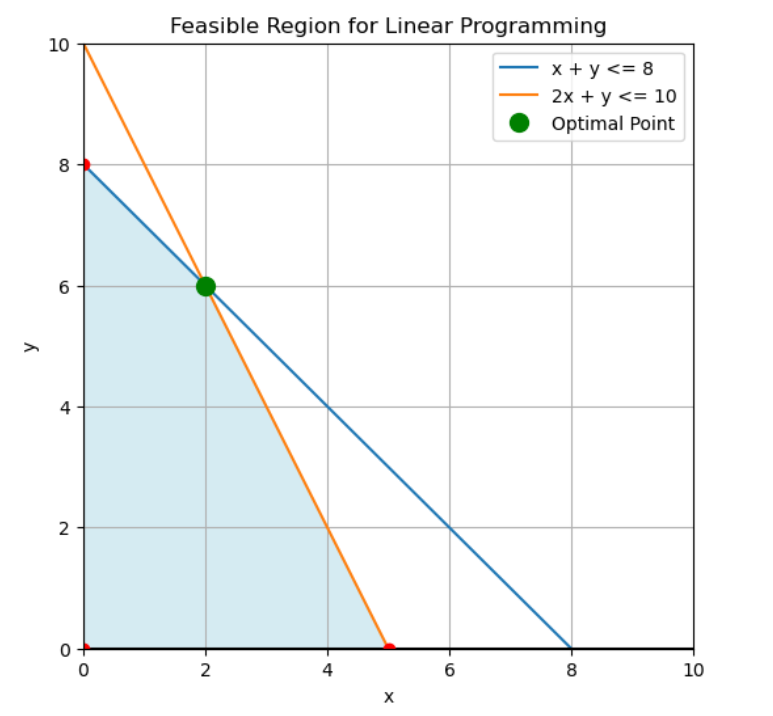
La programación lineal encuentra soluciones óptimas en los vértices de las regiones factibles definidas por restricciones. Imagen del autor

Métodos de solución y enfoques algorítmicos

Entender cómo funcionan los algoritmos cambió mi apreciación por llamar a linprog(). No se trata de cajas negras, sino de elegantes procedimientos matemáticos.

Algoritmo simplex

El algoritmo simplex, desarrollado por George Dantzig en 1947, es el punto de partida. Tu idea: recorrer sistemáticamente desde un vértice hasta el vértice adyacente, mejorando siempre el objetivo, hasta alcanzar el óptimo.

El algoritmo mantiene un cuadro y realiza operaciones pivotantes para desplazarse entre los vértices. Cada iteración mejora el objetivo o determina la optimización seleccionando un elemento pivote y actualizando mediante operaciones de fila.

from scipy.optimize import linprog
import numpy as np

c = [-3, -2]
A_ub = [[2, 1], [2, 3], [3, 1]]
b_ub = [18, 42, 24]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Optimal solution: x1 = {result.x[0]:.2f}, x2 = {result.x[1]:.2f}")
print(f"Maximum value: {-result.fun:.2f}")
print(f"Iterations: {result.nit}")

El código anterior muestra cómo resolver un problema de maximización con el método simplex negando los coeficientes del objetivo. El solucionador se mueve sistemáticamente entre los vértices de la región factible definida por las restricciones, alcanzando la solución óptima en solo unas pocas iteraciones. En problemas más grandes, el método simplex puede encontrar el óptimo en muchos menos pasos que el número de vértices factibles, a menudo en menos de 20 iteraciones, incluso con miles de posibilidades.

Métodos de punto interior

Mientras que el método simplex atraviesa los límites, los métodos de punto interior navegan por el interior de la región factible. En el caso de problemas de optimización de portafolio grandes con cientos de activos, el método simplex puede volverse lento, mientras que los métodos de punto interior resuelven los problemas en segundos.

La ventaja clave es la complejidad en tiempo polinomial. El algoritmo de Karmarkar (1984) hizo que los métodos de punto interior fueran prácticos, equilibrando la mejora objetiva con el alejamiento de los límites de restricción. Los solucionadores modernos como Gurobi seleccionan automáticamente entre simplex y punto interior en función de las características del problema.

Método gráfico para dos variables

En el caso de los problemas con dos variables, siempre los resuelvo primero gráficamente. Esto desarrolla la intuición que se transfiere a dimensiones superiores. Gráfico de las restricciones, identifica la región factible y encuentra qué esquina optimiza el objetivo.

from scipy.optimize import linprog

c = [-30, -40]
A_ub = [[2, 1], [1, 2]]
b_ub = [100, 80]
bounds = [(0, None), (0, None)]

result = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

print(f"Bread loaves: {result.x[0]:.0f}")
print(f"Cakes: {result.x[1]:.0f}")
print(f"Maximum profit: ${-result.fun:.0f}")

Este problema de producción de panadería maximiza los beneficios del pan y los pasteles, sujeto a las limitaciones de tiempo del horno y la decoración. La solución revela qué punto de esquina es óptimo desde el punto de vista geométrico, lo que concreta el comportamiento de salto de vértices del algoritmo.

Aplicaciones en todos los sectores

La programación lineal aplica el mismo marco matemático para resolver problemas en ámbitos muy diferentes.

Fabricación y producción

La planificación de la producción fue tu primera aplicación seria. El problema de la combinación de producción determina las cantidades de fabricación, con variables que representan la producción, objetivos que maximizan los beneficios y restricciones que reflejan las limitaciones de recursos.

from pulp import *

products = ['Phone', 'Tablet', 'Laptop']

profits = {'Phone': 120, 'Tablet': 200, 'Laptop': 350}
assembly_time = {'Phone': 2, 'Tablet': 3, 'Laptop': 5}
testing_time = {'Phone': 1, 'Tablet': 1.5, 'Laptop': 2}

assembly_available = 500
testing_available = 200
min_production = {'Phone': 50, 'Tablet': 30, 'Laptop': 20}

model = LpProblem("Production_Planning", LpMaximize)
production = LpVariable.dicts("produce", products, lowBound=0, cat='Integer')

model += lpSum([profits[p] * production[p] for p in products])
model += lpSum([assembly_time[p] * production[p] for p in products]) <= assembly_available
model += lpSum([testing_time[p] * production[p] for p in products]) <= testing_available

for p in products:
    model += production[p] >= min_production[p]

model.solve()

print(f"Status: {LpStatus[model.status]}")
for p in products:
    print(f"{p}: {production[p].varValue:.0f} units")
print(f"Total profit: ${value(model.objective):,.0f}")

El modelo anterior optimiza la producción electrónica en tres líneas de productos, equilibrando la capacidad de montaje y prueba con los requisitos mínimos de producción.

Los problemas de mezcla optimizan las mezclas que cumplen con las especificaciones a un costo mínimo, como la mezcla de alimentos para satisfacer los requisitos nutricionales y minimizar el costo.

Transporte y logística

El problema del transporte es otro ejemplo estudiado. La estructura clásica tiene fuentes con suministros y destinos con demandas, lo que minimiza el costo total de envío.

warehouses = ['Warehouse_A', 'Warehouse_B', 'Warehouse_C']
supply = {'Warehouse_A': 300, 'Warehouse_B': 400, 'Warehouse_C': 200}

customers = ['Customer_1', 'Customer_2', 'Customer_3', 'Customer_4']
demand = {'Customer_1': 200, 'Customer_2': 150, 'Customer_3': 250, 'Customer_4': 200}

costs = {
    ('Warehouse_A', 'Customer_1'): 8,  ('Warehouse_A', 'Customer_2'): 6,
    ('Warehouse_A', 'Customer_3'): 10, ('Warehouse_A', 'Customer_4'): 7,
    ('Warehouse_B', 'Customer_1'): 9,  ('Warehouse_B', 'Customer_2'): 12,
    ('Warehouse_B', 'Customer_3'): 8,  ('Warehouse_B', 'Customer_4'): 11,
    ('Warehouse_C', 'Customer_1'): 14, ('Warehouse_C', 'Customer_2'): 7,
    ('Warehouse_C', 'Customer_3'): 10, ('Warehouse_C', 'Customer_4'): 12,
}

model = LpProblem("Transportation", LpMinimize)

routes = [(w, c) for w in warehouses for c in customers]
shipments = LpVariable.dicts("ship", routes, lowBound=0)

model += lpSum([costs[i, j] * shipments[i, j] for (i, j) in routes])

for w in warehouses:
    model += lpSum([shipments[w, c] for c in customers]) <= supply[w]

for c in customers:
    model += lpSum([shipments[w, c] for w in warehouses]) >= demand[c]

model.solve()

Los problemas de flujo de red generalizan el transporte a gráficos con nodos de transbordo. He leído que las aerolíneas utilizan esto ampliamente para la programación de tripulaciones y las rutas de los aviones.

Servicios financieros y asistencia sanitaria

En las aplicaciones financieras, la presupuestación de capital selecciona los proyectos que maximizan el rendimiento sujeto a las restricciones presupuestarias:

projects = {
    'Project_A': {'return': 25000, 'cost': 100000, 'staff': 5},
    'Project_B': {'return': 30000, 'cost': 150000, 'staff': 7},
    'Project_C': {'return': 20000, 'cost': 80000, 'staff': 4},
}

budget = 300000
staff_available = 15

model = LpProblem("Capital_Budgeting", LpMaximize)
select = LpVariable.dicts("select", projects.keys(), cat='Binary')

model += lpSum([projects[p]['return'] * select[p] for p in projects])
model += lpSum([projects[p]['cost'] * select[p] for p in projects]) <= budget
model += lpSum([projects[p]['staff'] * select[p] for p in projects]) <= staff_available

model.solve()

Los sistemas sanitarios se enfrentan a infinitos retos de optimización. Consulté sobre un problema de programación clínica que asignaba turnos a las enfermeras respetando los requisitos de cualificación y el equilibrio de la carga de trabajo.

Aplicaciones de tecnología moderna

La programación lineal también aparece de forma inesperada en machine learning. La selección de características puede formularse como la minimización del error de predicción sujeto a restricciones de dispersión. La nube lo utiliza para la asignación de recursos en sistemas distribuidos.

Complejidad computacional y rendimiento

La complejidad es importante cuando los problemas pasan de ser ejemplos sencillos a sistemas de producción.

Complejidad del algoritmo simplex

Simplex tiene un nivel de complejidad fascinante. Tiene un rendimiento exponencial en el peor de los casos, pero excelente en el promedio. Los casos patológicos, como el cubo de Klee-Minty, obligan a examinar todos los vértices, pero los problemas típicos solo examinan una pequeña fracción, escalando aproximadamente de forma cuadrática.

Lo probé resolviendo problemas generados aleatoriamente de tamaño creciente:

import time
import numpy as np
from scipy.optimize import linprog

def benchmark_simplex(num_vars, num_constraints):
    c = np.random.randn(num_vars)
    A_ub = np.random.randn(num_constraints, num_vars)
    b_ub = np.random.rand(num_constraints) * 10
    
    start = time.time()
    result = linprog(c, A_ub=A_ub, b_ub=b_ub, method='simplex')
    elapsed = time.time() - start
    
    return elapsed, result.nit

problem_sizes = [(10, 20), (50, 100), (100, 200), (200, 400)]

for n_vars, n_const in problem_sizes:
    times, iterations = [], []
    for _ in range(10):
        t, it = benchmark_simplex(n_vars, n_const)
        times.append(t)
        iterations.append(it)
    print(f"{n_vars}x{n_const}: {np.mean(times):.4f}s, {np.mean(iterations):.1f} iterations")

Mis pruebas comparativas demostraron que duplicar el tamaño del problema aumentaba el tiempo en menos de cuatro veces, lo que confirma un comportamiento casi polinomial para distribuciones típicas.

Mejoras en el rendimiento

Los solucionadores modernos logran un rendimiento notable gracias al preprocesamiento, el procesamiento paralelo y la selección automática de algoritmos. El preprocesamiento puede reducir el tamaño del problema en un 30 % o más automáticamente antes de resolverlo.

La degeneración se produce cuando múltiples restricciones son estrictas en el punto óptimo, lo que puede provocar ciclos. Me encontré con este problema cuando dos rutas tenían costes idénticos. Los solucionadores utilizan técnicas de perturbación para evitar los ciclos, aunque los problemas degenerados se resuelven más lentamente.

La inestabilidad numérica surge con problemas mal escalados. La mezcla de cantidades monetarias (miles de dólares) con cantidades (unidades individuales) provocó advertencias del solucionador. El reescalado lo solucionó inmediatamente.

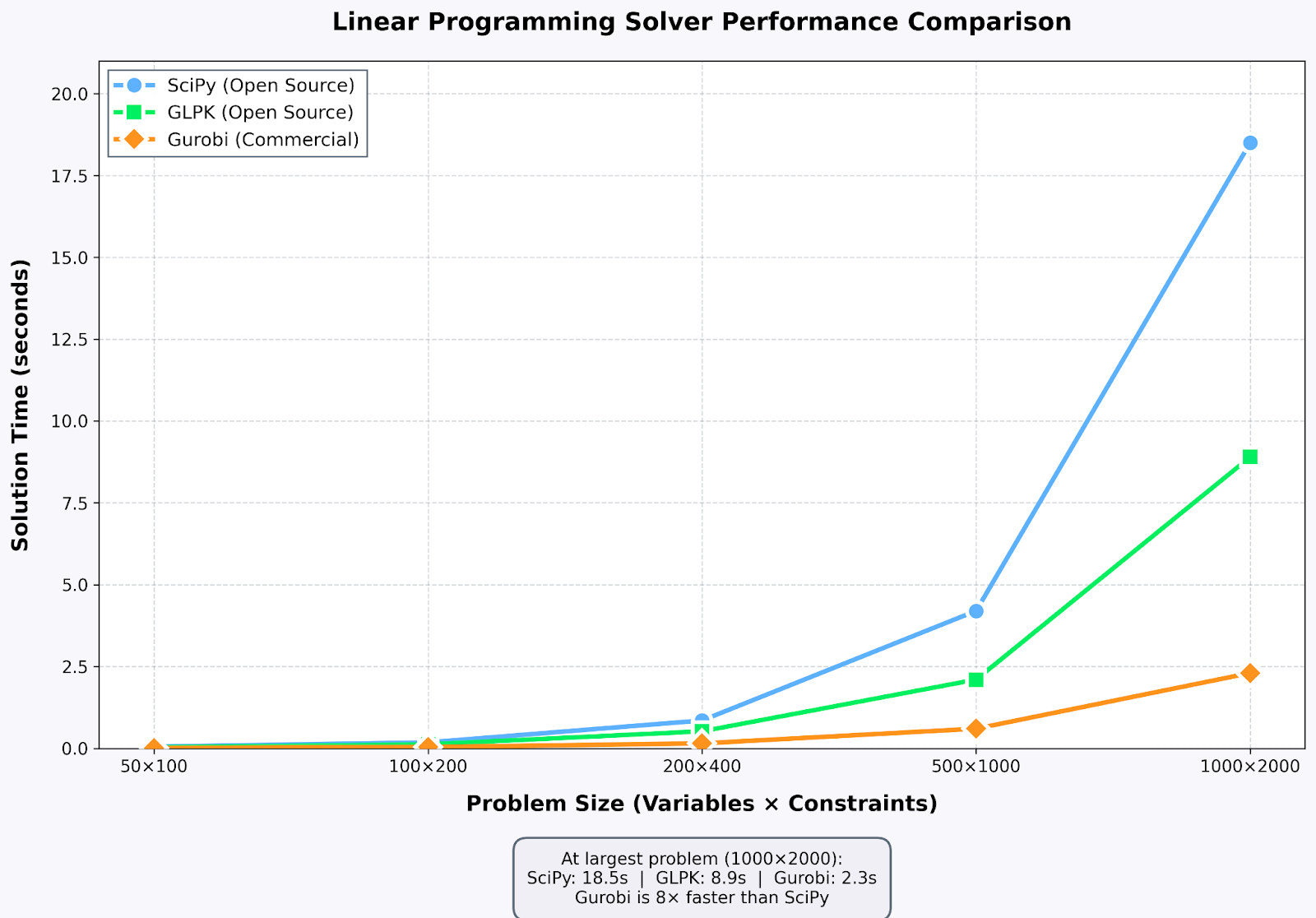
Comparación del rendimiento de los solucionadores: las soluciones comerciales destacan en problemas a gran escala. Imagen del autor

Herramientas de software e implementación

La elección de las herramientas influye enormemente en la productividad. He pasado de programar manualmente en simplex a utilizar solucionadores profesionales que manejan problemas mucho más complejos.

Solucionadores comerciales y lenguajes de modelado

CPLEX y Gurobi dominan la optimización industrial, ofreciendo un rendimiento mucho mejor que las alternativas de código abierto para problemas de gran envergadura. Utilicé la licencia académica de Gurobi para el trabajo relacionado con la cadena de suministro. Los problemas que te llevaban minutos resolver con SciPy ahora se resuelven en segundos.

PuLP es mi Python preferido. Proporciona una API limpia para formular modelos resueltos por varios backends:

from pulp import *

model = LpProblem("my_problem", LpMaximize)

x = LpVariable("x", lowBound=0)
y = LpVariable("y", lowBound=0)

model += 3*x + 2*y
model += x + y <= 100
model += 2*x + y <= 150

model.solve()

print(f"Used solver: {model.solver}")
print(f"Status: {LpStatus[model.status]}")

La capa de abstracción significa código independiente del solucionador que se ejecuta en diferentes sistemas. Pyomo ofrece funciones más avanzadas para la optimización compleja, incluida la programación no lineal y estocástica.

Alternativas en la nube y de código abierto

Las nubes ofrecen optimización como servicio para problemas irregulares a gran escala. Subes los datos del problema y recibes las soluciones a través de la API. La arquitectura sin servidor es elegante, aunque más lenta que los solucionadores locales para problemas pequeños.

GLPK (GNU Linear Programming Kit) es una herramienta fiable de código abierto. Lo utilizo para la enseñanza y para proyectos personales. HiGHS es un solucionador más reciente que ofrece un rendimiento impresionante. SciPy ha adoptado recientemente HiGHS como su backend predeterminado, y mis pruebas de rendimiento han demostrado que iguala a Gurobi en muchos problemas.

Ejemplos de programación lineal

Trabajar con ejemplos completos ayuda a comprender mejor que la teoría por sí sola.

Ejemplo 1: Problema de dieta

El problema clásico de la dieta es minimizar el costo y, al mismo tiempo, satisfacer las necesidades nutricionales:

from pulp import *

foods = {
    'Oatmeal': {'cost': 0.50, 'calories': 110, 'protein': 4, 'vitamin': 2},
    'Chicken': {'cost': 2.50, 'calories': 250, 'protein': 30, 'vitamin': 0},
    'Eggs':    {'cost': 0.80, 'calories': 155, 'protein': 13, 'vitamin': 1},
    'Milk':    {'cost': 1.20, 'calories': 150, 'protein': 8, 'vitamin': 4},
    'Bread':   {'cost': 0.30, 'calories': 80, 'protein': 3, 'vitamin': 0}
}

min_calories, min_protein, min_vitamin = 2000, 50, 10

model = LpProblem("Diet_Optimization", LpMinimize)
servings = LpVariable.dicts("servings", foods.keys(), lowBound=0)

model += lpSum([foods[f]['cost'] * servings[f] for f in foods])
model += lpSum([foods[f]['calories'] * servings[f] for f in foods]) >= min_calories
model += lpSum([foods[f]['protein'] * servings[f] for f in foods]) >= min_protein
model += lpSum([foods[f]['vitamin'] * servings[f] for f in foods]) >= min_vitamin

model.solve()

print(f"Total cost: ${value(model.objective):.2f}")
for food in foods:
    if servings[food].varValue > 0.01:
        print(f"{food}: {servings[food].varValue:.2f} servings")

La fórmula anterior encuentra la combinación más económica de alimentos que satisfacen las necesidades nutricionales diarias. Esto demuestra que las soluciones óptimas de LP no siempre son prácticas sin restricciones adicionales en cuanto a variedad, gustos o preferencias alimentarias.

Este mismo marco también puede servir de base para tomar decisiones empresariales, como optimizar los calendarios de producción o asignar presupuestos de marketing.

Ejemplo 2: Planificación multipériodo

La planificación multipériodo tiene en cuenta cómo los niveles de inventario afectan a las necesidades futuras en varios períodos de tiempo:

days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday']

centers = {
    'North': {'daily_demand': [100, 80, 90, 110, 85], 'capacity': 250},
    'South': {'daily_demand': [120, 100, 95, 105, 130], 'capacity': 300},
}

delivery_cost = {'Monday': 50, 'Tuesday': 50, 'Wednesday': 50,
                 'Thursday': 50, 'Friday': 70}

model = LpProblem("Multiperiod_Routing", LpMinimize)

deliveries = LpVariable.dicts("deliver",
                              [(c, d) for c in centers for d in days],
                              lowBound=0)
inventory = LpVariable.dicts("inventory",
                            [(c, d) for c in centers for d in days],
                            lowBound=0)

model += lpSum([delivery_cost[d] * deliveries[c, d] 
                for c in centers for d in days])

for c in centers:
    for i, day in enumerate(days):
        if i == 0:
            model += inventory[c, day] == deliveries[c, day] - centers[c]['daily_demand'][i]
        else:
            prev_day = days[i-1]
            model += (inventory[c, day] == inventory[c, prev_day] + 
                     deliveries[c, day] - centers[c]['daily_demand'][i])
        model += inventory[c, day] <= centers[c]['capacity']

model.solve()

Los modelos multipériodo aumentan la complejidad del problema, pero permiten una optimización sofisticada. El modelo consolida las entregas en los días más económicos, utilizando la capacidad de almacenamiento para reducir los costes generales.

Programación mixta entera

Muchos problemas implican decisiones discretas: construir una instalación o no, asignar un trabajador o no. Esto requiere programación mixta entera (MIP), que amplía la programación lineal con variables enteras y binarias.

Introducción y método de ramificación y limitación

Los problemas de enrutamiento requieren decisiones enteras. La variable binaria « x[i][j] » indica si el vehículo « i » visita la ubicación « j ». Los vehículos no pueden realizar visitas fraccionadas.

La búsqueda por ramificación y límite explora sistemáticamente un espacio de soluciones discretas resolviendo relajaciones LP continuas:

from pulp import *

model_continuous = LpProblem("Continuous", LpMaximize)
x_cont = LpVariable("x", lowBound=0)
y_cont = LpVariable("y", lowBound=0)

model_continuous += 3*x_cont + 4*y_cont
model_continuous += x_cont + 2*y_cont <= 10
model_continuous += 2*x_cont + y_cont <= 12

model_continuous.solve()
print(f"Continuous: x={x_cont.varValue:.2f}, y={y_cont.varValue:.2f}")

model_integer = LpProblem("Integer", LpMaximize)
x_int = LpVariable("x", lowBound=0, cat='Integer')
y_int = LpVariable("y", lowBound=0, cat='Integer')

model_integer += 3*x_int + 4*y_int
model_integer += x_int + 2*y_int <= 10
model_integer += 2*x_int + y_int <= 12

model_integer.solve()
print(f"Integer: x={x_int.varValue:.0f}, y={y_int.varValue:.0f}")

La solución entera difiere del redondeo de la solución continua. El método Branch-and-bound encuentra la solución entera óptima, pero con un coste computacional significativamente mayor.

Cuándo utilizar la programación entera

Utiliza variables enteras cuando las decisiones sean intrínsecamente discretas: apertura de instalaciones, asignación de trabajadores, rutas de vehículos. Las optimizaciones en el mercado de bonos suelen requerir soluciones mixtas enteras. Las variables continuas pueden producir asignaciones fraccionarias sin sentido, mientras que las variables binarias producen soluciones implementables.

Sin embargo, la programación entera es mucho más costosa. Los problemas con cientos de variables enteras pueden tardar horas, frente a segundos en el caso de los LP continuos. Si las cantidades de producción son grandes, la integridad importa menos, ya que el redondeo apenas afecta a las soluciones. Resuelve siempre primero la relajación continua para comprobar los límites antes de pasar a la programación entera completa.

Conclusión

La programación lineal transforma la forma en que abordas los problemas de optimización. El mismo marco matemático se aplica en ámbitos muy diferentes, desde el enrutamiento hasta la planificación de la producción o la gestión de portafolio.

Comienza con problemas sencillos de dos variables que puedas visualizar geométricamente. Implementa el método simplex básico para comprender qué hacen los solucionadores comerciales entre bastidores. Trabaja con fórmulas reales, traduciendo los requisitos empresariales en restricciones matemáticas.

Para profundizar tus conocimientos, explora nuestros cursos Introducción a la optimización en Python y Álgebra lineal para la ciencia de datos, que te permitirán reforzar tus bases matemáticas. Nuestro programa profesional como científico de machine learning en Python es otra excelente opción.