Descomposición QR para el aprendizaje automático

La descomposición QR es una técnica fundamental de factorización de matrices muy utilizada en diversos campos de la ciencia de datos y el aprendizaje automático. Su capacidad para descomponer matrices complejas en piezas más sencillas lo convierte en un método muy necesario para resolver problemas de álgebra lineal y mejorar la estabilidad de los algoritmos.

Tanto si realizas una regresión lineal por mínimos cuadrados ordinarios como si construyes motores de recomendación en Python o PySpark, comprender la descomposición QR puede aumentar significativamente tu capacidad para trabajar con grandes conjuntos de datos y modelos matemáticos complejos. 

¿Qué es la descomposición QR?

Cuando factorizas, o descompones, una matriz, expresas esa matriz como el producto de dos o más matrices. En otras palabras, la factorización matricial te permite descomponer una matriz en componentes más simples, que, al multiplicarse entre sí mediante la multiplicación matricial, reconstruirán la matriz original. Nos interesa la factorización de matrices porque simplifica muchos problemas de álgebra lineal, haciéndolos más fáciles de resolver. 

La descomposición QR es un tipo específico de técnica de factorización matricial que se utiliza para factorizar una matriz en el producto de una matriz ortogonal Q y una matriz triangular superior R. La ecuación que vemos habitualmente es A = QR. 

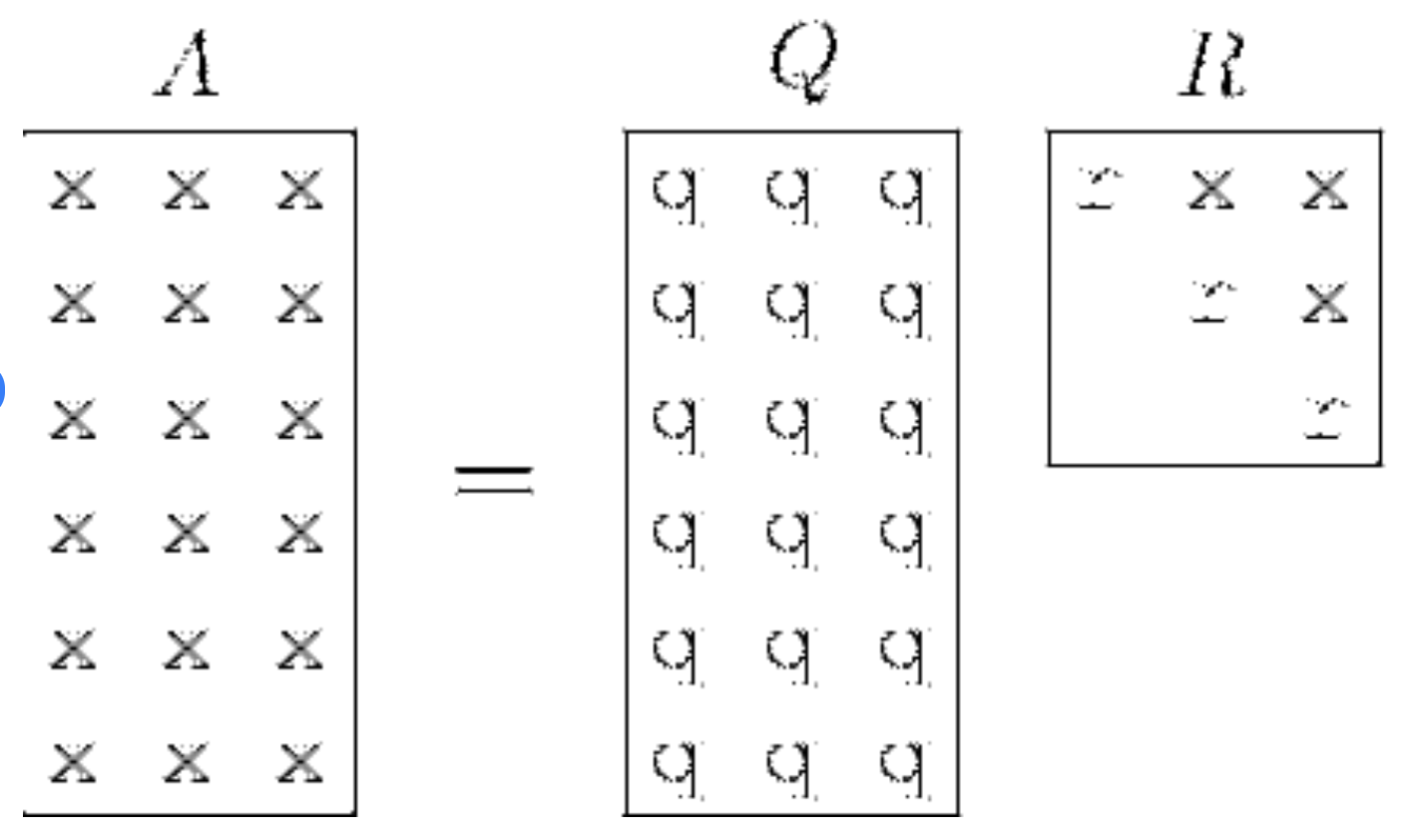
Descomposición QR visualizada. Fuente: ResearchGate

Para entender la descomposición QR, tienes que comprender que en álgebra lineal, la multiplicación de matrices no sigue las mismas reglas intuitivas que la multiplicación escalar. En concreto, la multiplicación de matrices no es conmutativa, es decir, AB ≠ BA en general, y por tanto, la noción de "inverso" es más compleja.

¿Qué son las Matrices Q y R?

Veamos las dos matrices importantes, Q y R.

Matriz ortogonal Q

Una matriz ortogonal Q se caracteriza por la propiedad de que su transpuesta es también su inversa, lo que se representa matemáticamente como ^QTQ= ^QQT = I , donde I es la matriz identidad. Transponer, por contexto, significa voltear la matriz sobre su diagonal.

Una matriz ortogonal también se caracteriza porque sus columnas forman una base ortonormal. Esto significa dos cosas: Por un lado, las columnas son ortogonales, es decir, el producto punto de cualquier par de columnas distintas de la matriz es cero. Y dos, cada columna tiene una magnitud, o unidad de longitud, de uno.

Es bueno trabajar con matrices ortogonales porque conservan las longitudes de los vectores y sus productos escalares. Así, si tienes un vector y lo multiplicas por una matriz ortogonal, la longitud de ese vector sigue siendo la misma. Además, si tienes dos vectores y los multiplicas a ambos por la misma matriz ortogonal, el producto punto entre ellos también sigue siendo el mismo. Por último, como las matrices ortogonales conservan las longitudes y los productos escalares, no distorsionan las propiedades geométricas de los vectores tras nuestra transformación. Es decir, si dos vectores son perpendiculares antes de la transformación, seguirán siendo perpendiculares después de aplicar la matriz ortogonal. 

Matriz triangular superior R

Una matriz triangular superior R es un tipo de matriz en la que todos los elementos por debajo de la diagonal principal son cero. Esta forma simplifica las ecuaciones matriciales y es especialmente útil para resolver sistemas de ecuaciones lineales mediante sustitución retrospectiva u otro método. También podríamos decir que, en la descomposición QR, R representa el componente que capta la magnitud y la orientación de la matriz original.

Formas de realizar la descomposición QR

Echemos un vistazo rápido a algunas de las distintas formas de realizar la descomposición QR.

El proceso de Gram-Schmidt 

El proceso de Gram-Schmidt es un algoritmo que se utiliza para convertir sistemáticamente un conjunto de vectores linealmente independientes en un conjunto ortonormal. Este proceso se utiliza específicamente para construir la matriz Q en nuestra descomposición QR y, después de tener Q, podemos derivar R. 

Rotaciones Givens

Las rotaciones Givens son otro método de ayuda a la descomposición QR. Con las rotaciones de Givens, se aplica una serie de rotaciones planas para introducir ceros por debajo de la diagonal de la matriz A. Cada rotación actúa sobre un par de coordenadas, conservando la longitud del vector y transformando la matriz en una forma triangular superior. Este método es eficaz para matrices dispersas, ya que sólo modifica una pequeña parte de la matriz en cada paso.

Reflexiones de los propietarios

Las reflexiones de Householder son una técnica más general que utiliza matrices de reflexión, conocidas como matrices de Householder, para eliminar sistemáticamente los elementos subdiagonales de la matriz A. Cada matriz Householder refleja un vector a través de un plano ortogonal al vector elegido para poner a cero una columna por debajo de la diagonal. El resultado es una matriz ortogonal Q, y una matriz triangular superior R. Las reflexiones de Householder son especialmente buenas para las matrices densas por su estabilidad numérica.

Implementación de la descomposición QR en R

En este apartado, practicaremos la descomposición QR en R utilizando tanto la función incorporada qr() para una implementación rápida, como recorriendo el proceso desde cero utilizando el proceso de Gram-Schmidt para construir nuestra intuición. Empecemos creando matrix_A, que utilizaremos en ambas secciones.  

matrix_A <- matrix(c(21, 21, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.2, 17.8, 16.4, 17.3, 15.2, 10.4, 10.4, 14.7, 32.4, 30.4, 33.9, 21.5, 15.5, 15.2, 13.3, 19.2, 27.3, 26, 30.4, 15.8, 19.7, 15, 21.4, 
              2.62, 2.875, 2.32, 3.215, 3.44, 3.46, 3.57, 3.19, 3.15, 3.44, 3.44, 4.07, 3.73, 3.78, 5.25, 5.424, 5.345, 2.2, 1.615, 1.835, 2.465, 3.52, 3.435, 3.84, 3.845, 1.935, 2.14, 1.513, 3.17, 2.77, 3.57, 2.78, 
              110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, 180, 180, 205, 215, 230, 66, 52, 65, 97, 150, 150, 245, 175, 66, 91, 113, 264, 175, 335, 109), 
            nrow = 32, ncol = 3, byrow = FALSE)

# Add column names
colnames(matrix_A) <- c("column_1", "column_2", "column_3")

Descomposición QR mediante la función qr()

Podemos hacer esta factorización en un solo paso con la función qr(). Asignamos el resultado a un objeto qr_decomp, que es una lista que contiene la descomposición QR. 

# Perform and Display the QR decomposition
(qr_decomp <- qr(matrix_A))

Cuando accedemos al componente de rango del objeto de descomposición QR, podemos ver el número de columnas linealmente independientes de nuestra matriz descompuesta. La salida indica que la matriz tiene un rango de tres, lo que significa que hay tres columnas linealmente independientes, que es lo que esperamos. Cuando accedemos al componente pivote, podemos ver información sobre la permutación de columnas utilizada durante el proceso de descomposición. La salida indica que las columnas de la matriz no se permutaron durante la descomposición, ya que los índices de los pivotes coinciden con el orden original de las columnas.

qr_decomp$rank
qr_decomp$pivot

[1] 3
[1] 1 2 3

Como paso siguiente, podemos acceder a la matriz Q y a la matriz R utilizando las funciones qr.Q() y qr.R(), respectivamente. Podemos ver en la salida que la matriz Q es rectangular y la matriz R es cuadrada con ceros debajo de la diagonal. 

# Extract and Display the Q and R matrices
(Q_matrix <- qr.Q(qr_decomp))
(R_matrix <- qr.R(qr_decomp))

           [,1]         [,2]         [,3]
 [1,] -0.17721481  0.023462372 -0.015872336
 [2,] -0.17721481 -0.001889138 -0.060272525
 [3,] -0.19240465  0.077625112 -0.019039920
 [4,] -0.18059033 -0.030282834 -0.118470211
 [5,] -0.15780557 -0.089157964  0.064671266
 [6,] -0.15274229 -0.099258795 -0.187022354
 [7,] -0.12067485 -0.161573766  0.277715036
 [8,] -0.20590673  0.012764996 -0.275768785
 [9,] -0.19240465 -0.004891570 -0.156509401
[10,] -0.16202497 -0.082397566 -0.117343880
[11,] -0.15021065 -0.101326680 -0.120852866
[12,] -0.13839633 -0.182888939 -0.033166125
[13,] -0.14599125 -0.136918208  0.028289904
[14,] -0.12826977 -0.170282764  0.014320506
[15,] -0.08776353 -0.381326588 -0.165554550
[16,] -0.08776353 -0.398625266 -0.160607236
[17,] -0.12405037 -0.332631845 -0.083208412
[18,] -0.27341714  0.219354877 -0.069242665
[19,] -0.25653954  0.250472633 -0.021737724
[20,] -0.28607534  0.275923528 -0.005454217
[21,] -0.18143421  0.045632512 -0.033447865
[22,] -0.13080141 -0.140377926 -0.045388530
[23,] -0.12826977 -0.135983661 -0.031340393
[24,] -0.11223605 -0.201937338  0.228196652
[25,] -0.16202497 -0.122661730 -0.004593473
[26,] -0.23037925  0.176744505 -0.035884026
[27,] -0.21940881  0.138786843  0.013273146
[28,] -0.25653954  0.260613237  0.211010230
[29,] -0.13333305 -0.101525496  0.418085457
[30,] -0.16624437 -0.009027316  0.183837006
[31,] -0.12658201 -0.152109209  0.596664759
[32,] -0.18059033  0.012963861 -0.046253102

      column_1  column_2  column_3
[1,] -118.5003 -16.11602 -711.9200
[2,]    0.0000 -10.05857 -496.9319
[3,]    0.0000   0.00000  283.7369

Como último paso, por curiosidad, podemos comprobar qué método utiliza la función qr() para la descomposición. 

?qr

Podemos ver lo siguiente como parte de la salida:  

The function computes the QR decomposition of a matrix using the LINPACK or LAPACK routine dgeqrf.

Si consultáramos la documentación de FORTRAN, veríamos que dgeqrf es una rutina LAPACK que utiliza transformaciones Householder. 

Descomposición QR desde cero

Intentemos comprender lo que ocurre con la función qr() recreando nosotros mismos, no la misma implementación, sino una idea similar, siguiendo el proceso y el pensamiento de Graham-Schmidt. El objetivo de este ejercicio no es recrear un método exacto, sino construir nuestra comprensión.

Construir la matriz Q

Para empezar a crear nuestra matriz Q mediante el proceso Graham-Schmidt, tenemos que normalizar la primera columna de los datos del subconjunto para obtener la primera columna de Q. El objetivo aquí es transformar nuestro conjunto de vectores de la matriz A en un nuevo conjunto de vectores de longitud unitaria uno, y asegurarnos de que estos vectores son ortogonales entre sí.

Para hallar la primera columna de Q, extraemos la primera columna de A, calculamos la norma euclídea y, a continuación, realizamos la normalización.

Para repasar, la norma euclídea es una medida de la longitud o magnitud de un vector en el espacio euclídeo. Consideramos la distancia desde el origen hasta el final del vector cuando consideramos cada elemento del vector como una coordenada en el espacio multidimensional. Para un vector v = [v1,v2,...,vn], su norma euclidiana se calcula de la siguiente manera:

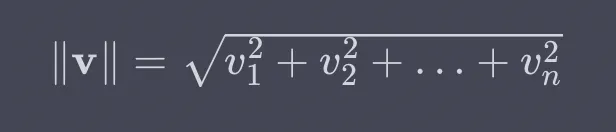
Así que, para implementarlo en R, elevamos al cuadrado cada columna, tomamos la suma, luego la raíz cuadrada y, por último, normalizamos.

# Extract the first column of the subset data
col_1 <- matrix_A[, 1]

# Calculate the Euclidean norm of the first column
norm_col_1 <- sqrt(sum(col_1^2))

# Normalize and display the first column to get the first column of Q
(q1 <- col_1 / norm_col_1)

Lo segundo que tenemos que repasar del álgebra lineal es el concepto de proyección. Una proyección es una operación matemática que proyecta un vector sobre un subespacio. El subespacio puede considerarse un espacio de menor dimensión dentro del espacio vectorial mayor. La proyección resultante es un vector que se encuentra dentro del subespacio y es el más próximo al vector original que se proyecta, que también es ortogonal al subespacio. 

Intentemos visualizarlo con la siguiente gráfica, donde la proyección p es el punto más cercano a a desde b, que debe ser perpendicular a b.

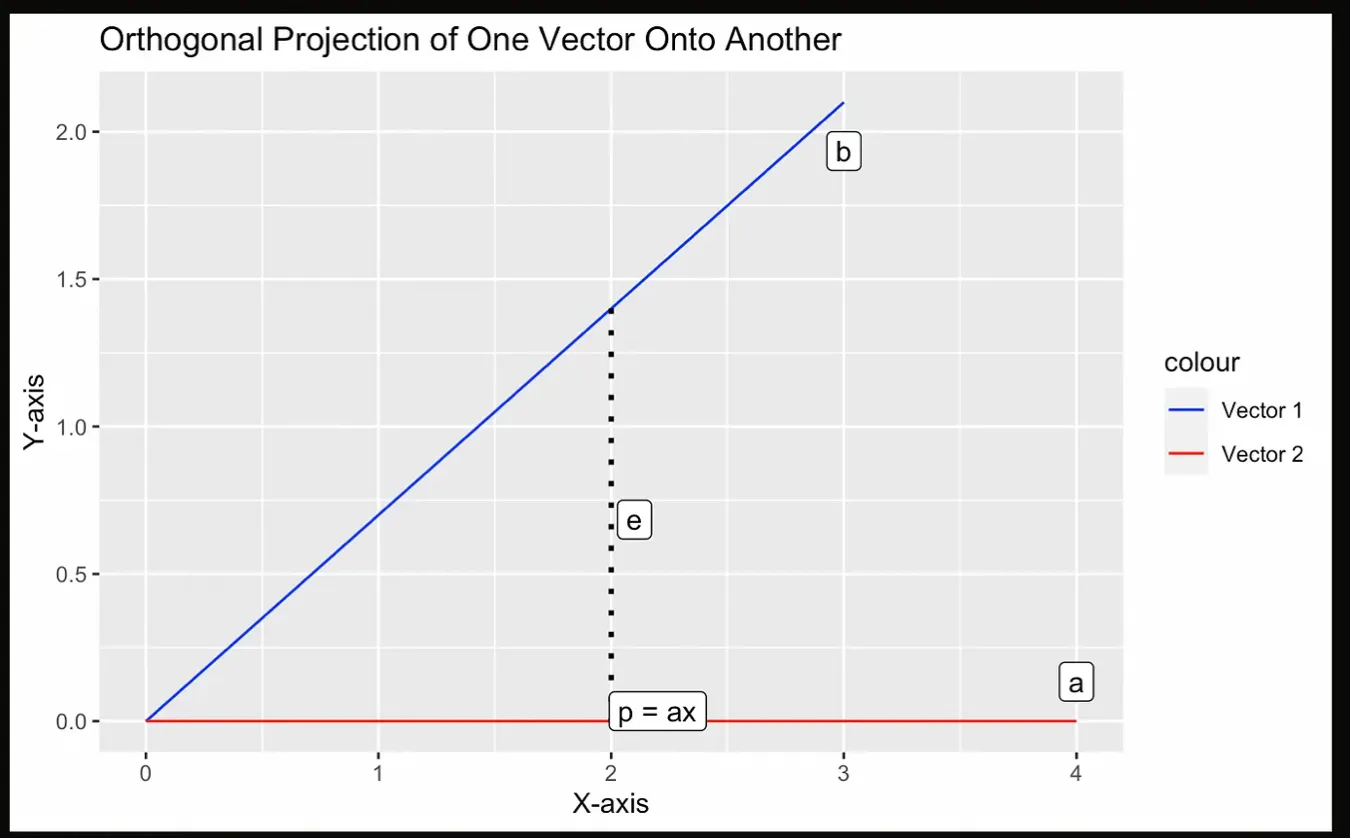
Ilustración de una proyección. Imagen del autor.

En el siguiente paso de la factorización QR, calculamos el segundo vector ortogonal calculando primero la proyección de la segunda columna de A sobre la primera columna de Q, y luego restando ese resultado de la segunda columna de A. El vector resultante será ortogonal al primer vector. Como paso final, normalizamos este vector para obtener la segunda columna de Q.

Repasemos la ecuación para una proyección. La proyección es la matriz que es a por a-transpuesta sobre el valor escalar que es a-transpuesta por a, multiplicado por b.

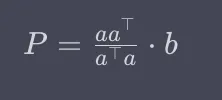
O, alternativamente:

Podríamos preguntarnos: ¿En qué se parecen estos dos métodos? Pues bien, si nos fijamos en la primera ecuación anterior, la parte situada a la izquierda de b calcula una matriz que captura esencialmente la dirección definida por el vector a y el factor de escala de esa dirección. Esto es similar al cálculo del vector unitario de a en el método del producto punto. 

El siguiente código R calcula la proyección del vector col_2 sobre el vector q1 utilizando el método del producto punto.

# Extract the second column of the subset data
col_2 <- matrix_A[, 2]

# Calculate the projection of col_2 onto q1
projection_col_2_q1 <- sum(col_2 * q1) * q1

# Calculate the second orthogonal vector
v2 <- col_2 - projection_col_2_q1

# Calculate the Euclidean norm of the second orthogonal vector
norm_v2 <- sqrt(sum(v2^2))

# Normalize the second orthogonal vector to get the second column of Q
q2 <- v2 / norm_v2

Como podemos ver en el código anterior, construir el segundo vector ortogonal y la columna correspondiente de la matriz Q implica un proceso de proyección, sustracción y normalización. Los pasos básicos son similares a los de la creación de la primera columna de Q, pero son un poco diferentes y algo más complicados: Primero extraemos la segunda columna de A; después creamos una proyección sobre el primer vector de Q; a continuación restamos la proyección de la segunda columna de A; después realizamos la normalización; por último, creamos la segunda columna de Q.

Podemos repetir este segundo paso para q3 hasta la última columna. En nuestro caso, los vectores ortogonales q1, q2, y q3 ​forman la base de la matriz ortogonal Q. Estos vectores son esenciales porque proporcionan la base para expresar los datos originales en un nuevo sistema de coordenadas.

Aquí vemos que el proceso de Gram-Schmidt es un proceso iterativo que garantiza que cada vector sucesivo es ortogonal a los anteriores. También recordamos que ortogonalidad significa que el producto punto de dos vectores es cero, lo que indica que son perpendiculares entre sí en el espacio vectorial. Confirmemos la ortogonalidad de q1 y q2 utilizando su producto punto:

# Calculate the dot product of q1 and q2
dot_product_q1_q2 <- sum(q1 * q2)

# Print the dot product to confirm orthogonality
print(dot_product_q1_q2)

[1] 2.43295e-16

Construir la matriz R

Ahora que tenemos nuestra matriz Q, tenemos que construir la matriz R. La matriz R de la descomposición QR contiene información sobre las relaciones entre las columnas de la matriz ortogonal Q y el conjunto de datos original. Es una matriz triangular superior, y cada elemento de la parte triangular superior de R se obtiene calculando el producto punto de las columnas correspondientes de Q y los datos originales.

Para construir la matriz triangular superior R, tenemos que calcular los productos punto de cada columna de Q con cada columna del conjunto de datos original. Esto dará como resultado una matriz que tiene el mismo número de filas que el número de columnas de Q, y será triangular superior debido a nuestro proceso anterior.

matrix_A <- matrix_A %>% as.matrix()

# Calculate and display the R matrix by multiplying Q^T and the subset data
R_matrix <- t(Q_matrix) %*% matrix_A

Vemos que la salida de nuestra matriz R tiene un aspecto un poco diferente esta vez. La razón es que la función qr() utiliza reflexiones de Householder con más estabilidad numérica que el proceso inspirado en Graham-Schmidt que creamos nosotros mismos.

         column_1      column_2  column_3
[1,] -1.185003e+02 -1.611602e+01 -711.9200
[2,]  5.814446e-16 -1.005857e+01 -496.9319
[3,]  7.633287e-15  1.338669e-15  283.7369

Podemos verificar la reconstrucción multiplicando Q y R y viendo que recuperamos matrix_A. Aquí, %*% es para la multiplicación de matrices en R.  

Q_matrix %*% R_matrix

   column_1 column_2 column_3
 [1,]     21.0    2.620      110
 [2,]     21.0    2.875      110
 [3,]     22.8    2.320       93
 [4,]     21.4    3.215      110
 [5,]     18.7    3.440      175
 [6,]     18.1    3.460      105
 [7,]     14.3    3.570      245
 [8,]     24.4    3.190       62
 [9,]     22.8    3.150       95
[10,]     19.2    3.440      123
[11,]     17.8    3.440      123
[12,]     16.4    4.070      180
[13,]     17.3    3.730      180
[14,]     15.2    3.780      180
[15,]     10.4    5.250      205
[16,]     10.4    5.424      215
[17,]     14.7    5.345      230
[18,]     32.4    2.200       66
[19,]     30.4    1.615       52
[20,]     33.9    1.835       65
[21,]     21.5    2.465       97
[22,]     15.5    3.520      150
[23,]     15.2    3.435      150
[24,]     13.3    3.840      245
[25,]     19.2    3.845      175
[26,]     27.3    1.935       66
[27,]     26.0    2.140       91
[28,]     30.4    1.513      113
[29,]     15.8    3.170      264
[30,]     19.7    2.770      175
[31,]     15.0    3.570      335
[32,]     21.4    2.780      109