Explicación de la distancia Hamming: Teoría y aplicaciones

Las métricas de distancia proporcionan formas esenciales de medir las diferencias entre objetos. Mientras que métricas como la distancia euclidiana o la distancia de Manhattan miden las diferencias espaciales, la distancia de Hamming adopta un enfoque diferente: Cuenta las posiciones en las que difieren dos secuencias. Esto la hace especialmente valiosa para la detección de errores, la validación de datos y la teoría de la información.

Desarrollada originalmente por Richard Hamming en 1950 mientras trabajaba en sistemas de verificación de códigos en los Laboratorios Bell, la distancia Hamming ha evolucionado más allá de sus raíces en las telecomunicaciones. Hoy en día, sirve como métrica clave en diversos campos, entre ellos:

• Validación de datos y comprobación de integridad
• Análisis de secuencias de ADN en bioinformática
• Concordancia de patrones en la recuperación de información
• Comparación de características en el aprendizaje automático

En esta guía, exploraremos cómo funciona la distancia de Hamming, examinaremos sus aplicaciones prácticas y la implementaremos en Python y R. Los conceptos e implementaciones que cubriremos mejorarán tu capacidad para resolver problemas de validación de datos, bioinformática y aprendizaje automático.

¿Qué es la distancia de Hamming?

La distancia de Hamming mide el número de posiciones en las que dos cadenas de igual longitud tienen símbolos diferentes. Piensa que se trata de contar el número mínimo de sustituciones necesarias para transformar una cadena en otra.

Por ejemplo, comparando dos cadenas binarias:

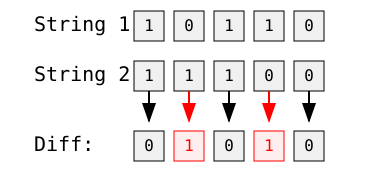
Imagen del autor

La distancia de Hamming aquí es 2 porque las cadenas difieren en dos posiciones: el segundo y el cuarto bits.

Matemáticamente, para dos cadenas x e y de igual longitud n, la distancia de Hamming D(x,y) se expresa como:

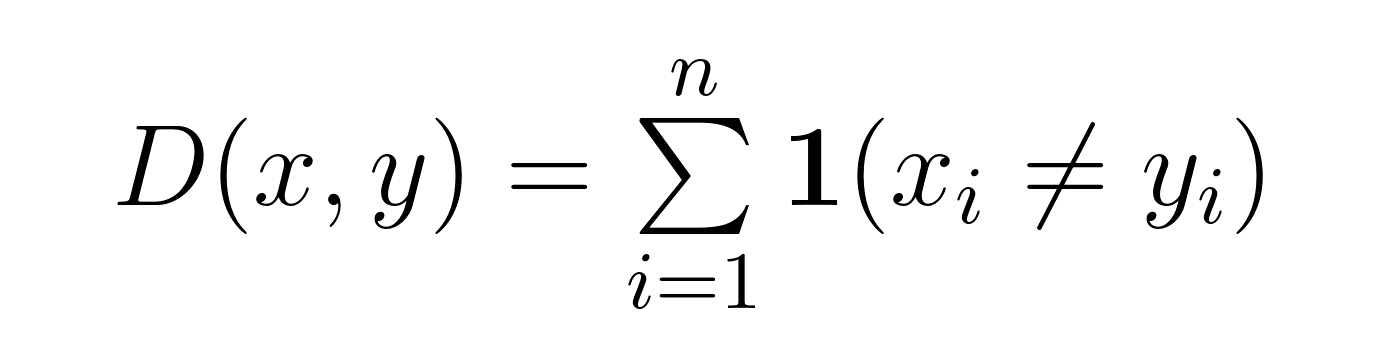
Esta fórmula cuenta las posiciones en las que xᵢ ≠ yᵢ. Para las cadenas binarias, esto se simplifica a contar dónde difieren los bits. Para otros tipos de secuencias (como ADN o texto), cuenta las posiciones con símbolos diferentes.

Dos propiedades clave a tener en cuenta:

1. Requiere cadenas de igual longitud.
2. Sólo cuenta las sustituciones, no las inserciones ni las supresiones.

Estas propiedades hacen que la distancia de Hamming sea ideal para escenarios en los que:

• Los datos consisten en códigos o secuencias de longitud fija.
• Sólo importan los errores de sustitución.
• Se necesitan comparaciones rápidas por posición.

Cómo funciona la distancia Hamming

Exploremos cómo calcular la distancia de Hamming a través de ejemplos, empezando con cadenas binarias sencillas y pasando a aplicaciones más complejas.

Ejemplo de cadena binaria

La aplicación más directa de la distancia de Hamming es la comparación de cadenas binarias. Analicemos dos cadenas de 8 bits:

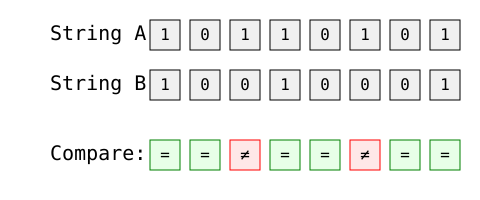
Imagen del autor

Cálculo paso a paso:

1. Posición 1: 1 = 1 (coincidencia)
2. Posición 2: 0 = 0 (coincidencia)
3. Posición 3: 1 ≠ 0 (diferencia)
4. Posición 4: 1 = 1 (coincidencia)
5. Posición 5: 0 = 0 (coincidencia)
6. Posición 6: 1 ≠ 0 (diferencia)
7. Posición 7: 0 = 0 (coincidencia)
8. Posición 8: 1 = 1 (coincidencia)

La distancia de Hamming es 2, ya que hay dos posiciones en las que las cadenas difieren (posiciones 3 y 6).

Ejemplo de secuencia de ADN

La distancia de Hamming se utiliza frecuentemente en bioinformática para comparar secuencias genéticas. Considera dos fragmentos de ADN:

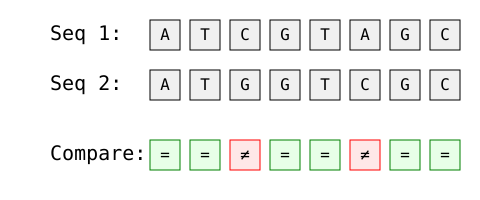
Imagen del autor

Análisis paso a paso:

1. Los pares de bases coinciden en las posiciones 1, 2, 4, 5, 7 y 8
2. Las diferencias se producen en las posiciones 3 (C→G) y 6 (A→C)
3. Distancia Hamming = 2 mutaciones

Esta comparación ayuda a los biólogos a cuantificar las mutaciones genéticas y a analizar la similitud del ADN.

Ejemplo de cadena de texto

La distancia de Hamming también funciona con cadenas de texto normales de igual longitud:

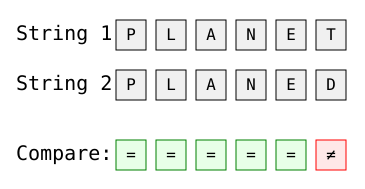
Imagen del autor

La distancia de Hamming aquí es 1, con la única diferencia en la última posición ("T" frente a "D").

Este tipo de comparación es útil en:

• Sistemas de corrección ortográfica
• Verificación OCR(Reconocimiento Óptico de Caracteres)
• Análisis de similitud de textos

Cada ejemplo demuestra cómo la distancia de Hamming proporciona una forma sencilla pero eficaz de cuantificar las diferencias entre secuencias, independientemente del tipo de datos que se comparen. La idea clave es que observa las diferencias en función de la posición e ignora la naturaleza específica de los cambios.

Aplicaciones de la distancia de Hamming

Detección y corrección de errores

La distancia de Hamming sentó las bases de los códigos de detección y corrección de errores en las comunicaciones digitales. Añadiendo estratégicamente bits de paridad para crear distancias mínimas entre las palabras clave válidas, los sistemas pueden detectar cuándo los datos recibidos no coinciden con los patrones válidos e incluso corregir los errores asignándolos a la palabra clave válida más próxima. Este principio impulsa tecnologías modernas como la memoria ECC (Código de Corrección de Errores) de los ordenadores, la corrección de errores de los códigos QR y los sistemas de comunicación del espacio profundo, donde la integridad de los datos es fundamental.

Teoría de la información

La teoría de la información utiliza la distancia de Hamming para diseñar sistemas de comunicación fiables. Al crear códigos de tratamiento de errores, los ingenieros se aseguran de que los mensajes válidos (codewords) difieran en un número mínimo específico de bits. Por ejemplo, si los mensajes válidos siempre difieren en al menos dos bits, el sistema puede detectar cuando un solo bit se corrompe durante la transmisión. Si los mensajes válidos difieren en al menos tres bits, el sistema puede incluso corregir errores de un solo bit identificando el mensaje válido más cercano. Estos principios ayudan a crear sistemas de comunicación robustos que se utilizan en todo, desde las comunicaciones por satélite hasta el almacenamiento de datos.

Bioinformática

Los investigadores genéticos utilizan la distancia de Hamming para analizar secuencias de ADN y cuantificar mutaciones. Comparando las secuencias genéticas posición por posición, los científicos pueden identificar mutaciones puntuales, seguir los cambios evolutivos y estudiar la diversidad genética. Esta aplicación resulta especialmente valiosa en el estudio de las mutaciones de las enfermedades, donde la comprensión de las posiciones exactas de los cambios genéticos ayuda a los investigadores a rastrear cómo evolucionan y se propagan las enfermedades en las poblaciones.

Aprendizaje automático

En el aprendizaje automático, la distancia de Hamming sirve como métrica de similitud para datos binarios o categóricos. Ayuda a comparar vectores de características en tareas de reconocimiento de patrones, medir la similitud en sistemas de recomendación y analizar datos categóricos en problemas de clasificación. La sencillez de la métrica y su cálculo eficiente la hacen especialmente valiosa cuando se trabaja con datos binarios de alta dimensión o cuando se necesitan cálculos rápidos de similitud para grandes conjuntos de datos.

Propiedades matemáticas

Propiedades del espacio métrico

La distancia de Hamming forma un espacio métrico matemático, lo que significa que sigue cuatro reglas fundamentales. En primer lugar, la distancia siempre es no negativa: no puedes tener un número negativo de posiciones en las que las cadenas difieran. En segundo lugar, la distancia entre dos secuencias es cero si y sólo si son idénticas. En tercer lugar, la distancia muestra simetría: comparar la secuencia A con la B da el mismo resultado que comparar la B con la A. Por último, satisface la desigualdad del triángulo: la distancia entre las secuencias A y C no puede ser mayor que la suma de las distancias de A a B y de B a C.

Propiedades de las cadenas binarias

Cuando se trabaja con cadenas binarias, la distancia de Hamming adquiere unas características especiales que la hacen especialmente útil para la detección de errores. Para dos cadenas binarias cualesquiera de longitud n, su distancia de Hamming no puede ser superior a n, sólo se produce cuando las cadenas son complementarias entre sí. La probabilidad de una determinada distancia de Hamming "d" entre dos cadenas binarias aleatorias sigue una distribución binomial, siendo la distancia más probable n/2. Esta propiedad ayuda a diseñar códigos de detección de errores que puedan reconocer cuándo se han volteado los bits durante la transmisión.

Distancia de Hamming en Python y R

Implementación en Python

Python ofrece tanto funciones de biblioteca incorporadas como implementaciones personalizadas para calcular la distancia de Hamming. La biblioteca SciPy proporciona la solución más eficaz gracias a sus funciones de distancia espacial:

from scipy.spatial.distance import hamming

# For working with strings
string1 = "1010101"
string2 = "1000101"

# Convert to list of integers for hamming function
arr1 = [int(bit) for bit in string1]
arr2 = [int(bit) for bit in string2]

# Calculate Hamming distance
distance = hamming(arr1, arr2) * len(arr1)  # Multiply by length because SciPy returns fraction
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

# For DNA sequences
sequence1 = "ATCGTACT"
sequence2 = "ATCGCACT"
distance = hamming(list(sequence1), list(sequence2)) * len(sequence1)
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

Para quienes prefieran una implementación personalizada:

def hamming_distance(str1: str, str2: str) -> int:
    """Calculate Hamming distance between two strings."""
    if len(str1) != len(str2):
        raise ValueError("Strings must be of equal length")
    return sum(c1 != c2 for c1, c2 in zip(str1, str2))

# Example usage
print(hamming_distance("1010101", "1000101"))  # Output: 1

Ejecución R

R proporciona una forma sencilla de calcular la distancia de Hamming utilizando funciones base:

hamming_distance <- function(str1, str2) {
    if (nchar(str1) != nchar(str2)) {
        stop("Strings must be equal length")
    }
    sum(strsplit(str1, "")[[1]] != strsplit(str2, "")[[1]])
}

# Example usage
hamming_distance("1010101", "1000101")
# [1] 1

# For DNA sequences
hamming_distance("ATCGTACT", "ATCGCACT")
# [1] 1

Para ampliar estos ejemplos de codificación y explorar más aplicaciones de las métricas de distancia en la práctica, consulta estos completos recursos:

• Diseño de flujos de trabajo de aprendizaje automático en Python - Aprende a implementar métricas de distancia en pipelines de aprendizaje automático y a integrarlas en tus flujos de trabajo de ML
• Análisis de conglomerados en R - Descubre cómo aplicar métodos basados en la distancia para agrupar y clasificar datos de forma eficaz

Estos cursos te ayudarán a ir más allá de las implementaciones básicas para comprender cómo afectan las métricas de distancia a las aplicaciones de aprendizaje automático, independientemente de tu lenguaje de programación preferido.

Hamming contra Otros enfoques

Imagen del autor

Distancia de Levenshtein (distancia de edición)

La distancia Levenshtein representa el número mínimo de ediciones de un solo carácter necesarias para cambiar una cadena por otra. A diferencia de la distancia de Hamming, puede manejar cadenas de longitudes diferentes al considerar las inserciones y supresiones junto con las sustituciones. Esta flexibilidad lo hace especialmente valioso para los correctores ortográficos, la alineación de secuencias de ADN y el emparejamiento difuso de cadenas, aunque esta versatilidad tiene el coste de una mayor complejidad computacional. Al comparar cadenas como "planeta" y "plan", la distancia de Levenshtein contaría la eliminación de 'e' y 't' como dos operaciones, mientras que la distancia de Hamming no podría hacer esta comparación en absoluto.

Distancia Damerau-Levenshtein

Basándose en la distancia Levenshtein estándar, la distancia Damerau-Levenshtein añade la transposición de caracteres adyacentes como operación válida. Esta adición lo hace especialmente eficaz para detectar errores tipográficos comunes en los que se intercambian caracteres accidentalmente. Por ejemplo, al comparar "forma" con "de", contaría esto como una única transposición en lugar de dos sustituciones separadas. Esta métrica se ha utilizado mucho en aplicaciones de procesamiento del lenguaje natural, sobre todo en sistemas automatizados de corrección ortográfica, en los que la transposición de caracteres es un error tipográfico frecuente.

Distancia Jaro-Winkler

La distancia Jaro-Winkler adopta un enfoque único al centrarse en los pesos de posición de los caracteres, favoreciendo especialmente las coincidencias al principio de las cadenas. En lugar de contar las operaciones de edición, produce una puntuación de similitud entre 0 y 1, donde 1 indica una coincidencia perfecta. Esta métrica destaca en la comparación de nombres propios y cadenas cortas, lo que la hace ideal para tareas de vinculación y deduplicación de registros. Por ejemplo, al comparar nombres como "Marta" y "Marhta", asignaría una puntuación de similitud más alta porque los caracteres que difieren aparecen más adelante en la cadena.

Elegir la métrica de distancia adecuada

Diferentes escenarios requieren diferentes métricas de distancia. Ten en cuenta estos factores clave a la hora de seleccionar tu enfoque:

Requisitos de velocidad y eficacia

• La distancia de Hamming ofrece el cálculo más rápido
• Levenshtein requiere más potencia de procesamiento
• Jaro-Winkler está entre los dos en cuanto a velocidad

Consideraciones sobre la longitud de la cadena

• Cadenas de longitud fija (datos binarios, códigos hash): Distancia Hamming
• Cadenas de longitud variable (entrada del usuario, texto natural): Distancia Levenshtein
• Cadenas cortas y nombres: Distancia Jaro-Winkler

Tipos de error a tratar 

• Sólo sustituciones: Distancia Hamming 
• Operaciones de edición completas: Distancia Levenshtein 
• Intercambio de personajes: Distancia Damerau-Levenshtein 
• Variaciones del nombre: Distancia Jaro-Winkler

Ámbito de aplicación

• Comunicación digital y detección de errores: Distancia Hamming
• Tratamiento de textos y corrección ortográfica: Distancia Levenshtein
• Deduplicación de bases de datos y correspondencia de registros: Distancia Jaro-Winkler
• Procesamiento del lenguaje natural: Distancia Damerau-Levenshtein

Esta comparación estructurada muestra cómo cada métrica de distancia sirve para fines distintos, siendo la distancia de Hamming especialmente valiosa en situaciones en las que su sencillez y velocidad se ajustan a los requisitos de comparación de longitud fija.

Conclusión

La elegancia de la distancia de Hamming reside en su sencillez. Al contar las posiciones en las que difieren las secuencias, proporciona una forma sólida de medir la disimilitud, tanto si detectas errores en los datos transmitidos como si analizas mutaciones genéticas. Esta métrica brilla especialmente en ámbitos en los que cada posición importa por igual y las sustituciones son la principal preocupación.

Cuando explores las métricas de distancia en tu propio trabajo, considera la distancia de Hamming cuando:

• Trabajar con secuencias de longitud fija
• Tratar con datos binarios o categóricos
• Construir sistemas de detección de errores
• Analizar secuencias genéticas
• Desarrollar algoritmos de concordancia de patrones

Para seguir desarrollando tu experiencia con las métricas de distancia y otros conceptos fundamentales de la ciencia de datos, explora nuestro programa de Certificación de Científico de Datos, disponible tanto en Python como en R.