Hamming Distance Explained: The Theory and Applications

Distance metrics provide essential ways to measure differences between objects. While metrics like Euclidean or Manhattan distance measure spatial differences, Hamming distance takes a different approach: It counts the positions where two sequences differ. This makes it particularly valuable for error detection, data validation, and information theory.

Originally developed by Richard Hamming in 1950 while working on code verification systems at Bell Labs, Hamming distance has evolved beyond its telecommunications roots. Today, it serves as a key metric in diverse fields including:

• Data validation and integrity checking
• DNA sequence analysis in bioinformatics
• Pattern matching in information retrieval
• Feature comparison in machine learning

In this guide, we'll explore how Hamming distance works, examine its practical applications, and implement it in Python and R. The concepts and implementations we'll cover will enhance your ability to solve problems in data validation, bioinformatics, and machine learning.

What is Hamming Distance?

Hamming distance measures the number of positions at which two strings of equal length have different symbols. Think of it as counting the minimum number of substitutions needed to transform one string into another.

For example, comparing two binary strings:

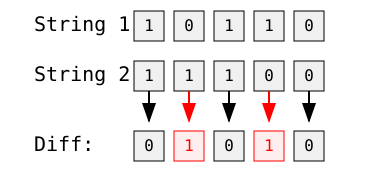
Image by Author

The Hamming distance here is 2 because the strings differ at two positions - the second and fourth bits.

Mathematically, for two strings x and y of equal length n, the Hamming distance D(x,y) is expressed as:

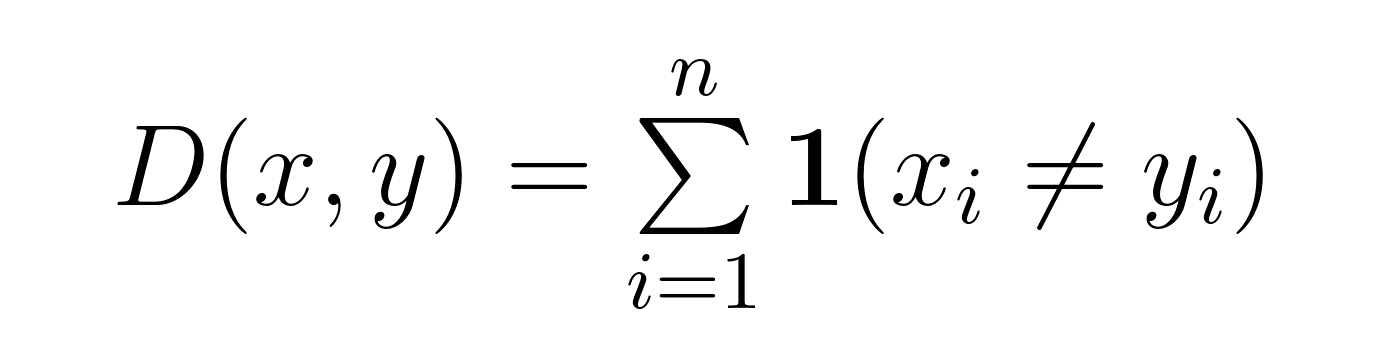
This formula counts positions where xᵢ ≠ yᵢ. For binary strings, this simplifies to counting where bits differ. For other types of sequences (like DNA or text), it counts positions with different symbols.

Two key properties to be aware of:

1. It requires strings of equal length.
2. It only counts substitutions, not insertions or deletions.

These properties make Hamming distance ideal for scenarios where:

• The data consists of fixed-length codes or sequences.
• Only substitution errors matter.
• Quick, position-wise comparisons are needed.

How Hamming Distance Works

Let's explore how to calculate Hamming distance through examples, starting with simple binary strings and moving to more complex applications.

Binary string example

The most straightforward application of Hamming distance is comparing binary strings. Let's analyze two 8-bit strings:

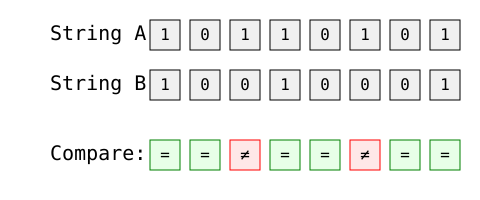
Image by Author

Step-by-step calculation:

1. Position 1: 1 = 1 (match)
2. Position 2: 0 = 0 (match)
3. Position 3: 1 ≠ 0 (difference)
4. Position 4: 1 = 1 (match)
5. Position 5: 0 = 0 (match)
6. Position 6: 1 ≠ 0 (difference)
7. Position 7: 0 = 0 (match)
8. Position 8: 1 = 1 (match)

The Hamming distance is 2, as there are two positions where the strings differ (positions 3 and 6).

DNA sequence example

Hamming distance is frequently used in bioinformatics to compare genetic sequences. Consider two DNA fragments:

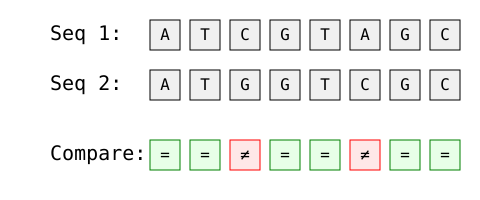
Image by Author

Step-by-step analysis:

1. Base pairs match at positions 1, 2, 4, 5, 7, and 8
2. Differences occur at positions 3 (C→G) and 6 (A→C)
3. Hamming distance = 2 mutations

This comparison helps biologists quantify genetic mutations and analyze DNA similarity.

Text string example

Hamming distance also works with regular text strings of equal length:

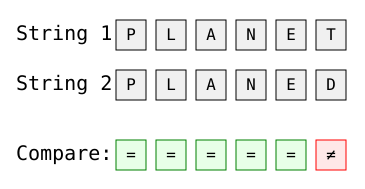
Image by Author

The Hamming distance here is 1, with the only difference at the last position ('T' vs 'D').

This type of comparison is useful in:

• Spell checking systems
• OCR (Optical Character Recognition) verification
• Text similarity analysis

Each example demonstrates how Hamming distance provides a simple yet effective way to quantify differences between sequences, regardless of the type of data being compared. The key insight is that it looks at position-wise differences while ignoring the specific nature of the changes.

Applications of Hamming Distance

Error detection and correction

Hamming distance laid the foundation for error-detecting and error-correcting codes in digital communications. By strategically adding parity bits to create minimum distances between valid codewords, systems can detect when received data doesn't match valid patterns and even correct errors by mapping to the nearest valid codeword. This principle powers modern technologies like ECC (Error-Correcting Code) memory in computers, QR code error correction, and deep space communication systems where data integrity is critical.

Information theory

Information theory uses Hamming distance to design reliable communication systems. When creating error-handling codes, engineers ensure valid messages (codewords) differ by specific minimum numbers of bits. For example, if valid messages always differ by at least two bits, the system can detect when a single bit gets corrupted during transmission. If valid messages differ by at least three bits, the system can even correct single-bit errors by identifying the closest valid message. These principles help create robust communication systems used in everything from satellite communications to data storage.

Bioinformatics

Genetic researchers use Hamming distance to analyze DNA sequences and quantify mutations. By comparing genetic sequences position by position, scientists can identify point mutations, track evolutionary changes, and study genetic diversity. This application proves particularly valuable in studying disease mutations, where understanding the exact positions of genetic changes helps researchers track how diseases evolve and spread through populations.

Machine learning

In machine learning, Hamming distance serves as a similarity metric for binary or categorical data. It helps compare feature vectors in pattern recognition tasks, measure similarity in recommendation systems, and analyze categorical data in classification problems. The metric's simplicity and efficient computation make it particularly valuable when working with high-dimensional binary data or when quick similarity calculations are needed for large datasets.

Mathematical Properties

Metric space properties

Hamming distance forms a mathematical metric space, which means it follows four fundamental rules. First, the distance is always non-negative - you can't have a negative number of positions where strings differ. Second, the distance between two sequences is zero if and only if they're identical. Third, the distance exhibits symmetry - comparing sequence A to B gives the same result as comparing B to A. Finally, it satisfies the triangle inequality: the distance between sequences A and C cannot be greater than the sum of distances from A to B and B to C.

Binary string properties

When working with binary strings, Hamming distance takes on special characteristics that make it particularly useful for error detection. For any two binary strings of length n, their Hamming distance can't exceed n, occurring only when the strings are complements of each other. The probability of a specific Hamming distance “d” between two random binary strings follows a binomial distribution, with the most likely distance being n/2. This property helps in designing error-detecting codes that can recognize when bits have been flipped during transmission.

Hamming Distance in Python and R

Python implementation

Python offers both built-in library functions and custom implementations for calculating Hamming distance. The SciPy library provides the most efficient solution through its spatial distance functions:

from scipy.spatial.distance import hamming

# For working with strings
string1 = "1010101"
string2 = "1000101"

# Convert to list of integers for hamming function
arr1 = [int(bit) for bit in string1]
arr2 = [int(bit) for bit in string2]

# Calculate Hamming distance
distance = hamming(arr1, arr2) * len(arr1)  # Multiply by length because SciPy returns fraction
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

# For DNA sequences
sequence1 = "ATCGTACT"
sequence2 = "ATCGCACT"
distance = hamming(list(sequence1), list(sequence2)) * len(sequence1)
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

For those who prefer a custom implementation:

def hamming_distance(str1: str, str2: str) -> int:
    """Calculate Hamming distance between two strings."""
    if len(str1) != len(str2):
        raise ValueError("Strings must be of equal length")
    return sum(c1 != c2 for c1, c2 in zip(str1, str2))

# Example usage
print(hamming_distance("1010101", "1000101"))  # Output: 1

R implementation

R provides a simple way to calculate Hamming distance using base functions:

hamming_distance <- function(str1, str2) {
    if (nchar(str1) != nchar(str2)) {
        stop("Strings must be equal length")
    }
    sum(strsplit(str1, "")[[1]] != strsplit(str2, "")[[1]])
}

# Example usage
hamming_distance("1010101", "1000101")
# [1] 1

# For DNA sequences
hamming_distance("ATCGTACT", "ATCGCACT")
# [1] 1

To build on these coding examples and explore more applications of distance metrics in practice, check out these comprehensive resources:

• Designing Machine Learning Workflows in Python - Learn how to implement distance metrics in machine learning pipelines and integrate them into your ML workflows
• Cluster Analysis in R - Discover how to apply distance-based methods for effective data clustering and classification

These courses will help you move beyond basic implementations to understand how distance metrics impact machine learning applications, regardless of your preferred programming language.

Hamming vs. Other Approaches

Image by Author

Levenshtein distance (edit distance)

The Levenshtein distance represents the minimum number of single-character edits required to change one string into another. Unlike Hamming distance, it can handle strings of different lengths by considering insertions and deletions alongside substitutions. This flexibility makes it particularly valuable for spell checkers, DNA sequence alignment, and fuzzy string matching, though this versatility comes at the cost of higher computational complexity. When comparing strings like "planet" and "plan", Levenshtein distance would count the deletion of 'e' and 't' as two operations, while Hamming distance couldn't make this comparison at all.

Damerau-Levenshtein distance

Building upon the standard Levenshtein distance, the Damerau-Levenshtein distance adds transposition of adjacent characters as a valid operation. This addition makes it especially effective at catching common typing errors where characters are accidentally swapped. For instance, in comparing "form" with "from", it would count this as a single transposition rather than two separate substitutions. This metric has found widespread use in natural language processing applications, particularly in automated spelling correction systems where character transposition is a common typing error.

Jaro-Winkler distance

The Jaro-Winkler distance takes a unique approach by focusing on character position weights, particularly favoring matches at the beginning of strings. Instead of counting edit operations, it produces a similarity score between 0 and 1, where 1 indicates a perfect match. This metric excels in comparing proper nouns and short strings, making it ideal for record linkage and deduplication tasks. For example, when comparing names like "Martha" and "Marhta", it would assign a higher similarity score because the differing characters appear later in the string.

Choosing the right distance metric

Different scenarios call for different distance metrics. Consider these key factors when selecting your approach:

Speed and efficiency requirements

• Hamming distance offers the fastest computation
• Levenshtein requires more processing power
• Jaro-Winkler falls between the two in terms of speed

String length considerations

• Fixed-length strings (binary data, hash codes): Hamming distance
• Variable-length strings (user input, natural text): Levenshtein distance
• Short strings and names: Jaro-Winkler distance

Error types to handle 

• Substitutions only: Hamming distance 
• Full edit operations: Levenshtein distance 
• Character swaps: Damerau-Levenshtein distance 
• Name variations: Jaro-Winkler distance

Application domain

• Digital communication and error detection: Hamming distance
• Text processing and spell checking: Levenshtein distance
• Database deduplication and record matching: Jaro-Winkler distance
• Natural language processing: Damerau-Levenshtein distance

This structured comparison shows how each distance metric serves distinct purposes, with Hamming distance particularly valuable in scenarios where its simplicity and speed align with fixed-length comparison requirements.

Conclusion

Hamming distance's elegance lies in its simplicity. By counting positions where sequences differ, it provides a robust way to measure dissimilarity, whether you're detecting errors in transmitted data or analyzing genetic mutations. This metric shines particularly bright in domains where every position matters equally and substitutions are the primary concern.

As you explore distance metrics in your own work, consider Hamming distance when:

• Working with fixed-length sequences
• Dealing with binary or categorical data
• Building error detection systems
• Analyzing genetic sequences
• Developing pattern matching algorithms

To continue building your expertise with distance metrics and other fundamental data science concepts, explore our Data Scientist Certification program, available in both Python and R.