La distance de Hamming expliquée : Théorie et applications

Les mesures de distance constituent des moyens essentiels pour mesurer les différences entre les objets. Alors que des mesures telles que la distance d' Euclide ou de Manhattan mesurent les différences spatiales, la distance de Hamming adopte une approche différente : Il compte les positions où deux séquences diffèrent. Elle est donc particulièrement utile pour la détection des erreurs, la validation des données et la théorie de l'information.

Développée à l'origine par Richard Hamming en 1950 alors qu'il travaillait sur des systèmes de vérification de code aux Bell Labs, la distance de Hamming a évolué au-delà de ses origines dans le domaine des télécommunications. Aujourd'hui, il sert de mesure clé dans divers domaines, notamment :

• Validation des données et contrôle de l'intégrité
• Analyse des séquences d'ADN en bio-informatique
• Correspondance de motifs dans la recherche d'informations
• Comparaison des caractéristiques dans l'apprentissage automatique

Dans ce guide, nous allons explorer le fonctionnement de la distance de Hamming, examiner ses applications pratiques et la mettre en œuvre en Python et en R. Les concepts et les mises en œuvre que nous allons couvrir amélioreront votre capacité à résoudre des problèmes de validation de données, de bio-informatique et d'apprentissage automatique.

Qu'est-ce que la distance de Hamming ?

La distance de Hamming mesure le nombre de positions où deux chaînes de même longueur ont des symboles différents. Il s'agit de compter le nombre minimum de substitutions nécessaires pour transformer une chaîne de caractères en une autre.

Par exemple, la comparaison de deux chaînes binaires :

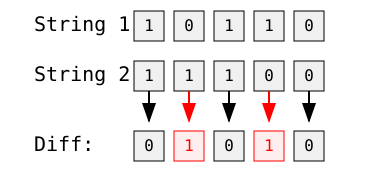
Image par l'auteur

La distance de Hamming est ici de 2 car les chaînes diffèrent à deux endroits : les deuxième et quatrième bits.

Mathématiquement, pour deux chaînes x et y de longueur égale n, la distance de Hamming D(x,y) est exprimée comme suit :

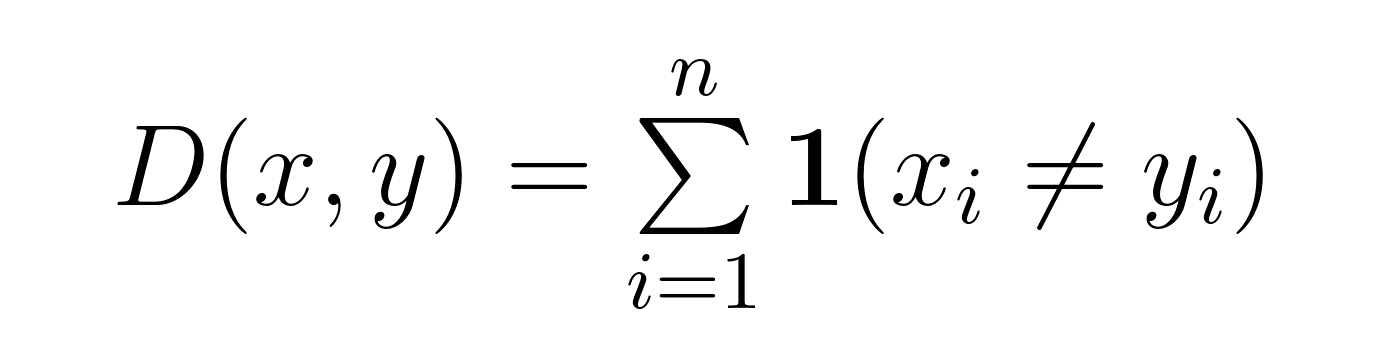
Cette formule compte les positions où xᵢ ≠ yᵢ. Pour les chaînes binaires, il suffit de compter les bits qui diffèrent. Pour d'autres types de séquences (comme l'ADN ou le texte), il compte les positions avec différents symboles.

Deux propriétés essentielles à connaître :

1. Il faut des chaînes de longueur égale.
2. Il ne compte que les substitutions, pas les insertions ou les suppressions.

Ces propriétés font de la distance de Hamming un outil idéal pour les scénarios dans lesquels :

• Les données sont constituées de codes ou de séquences de longueur fixe.
• Seules les erreurs de substitution comptent.
• Des comparaisons rapides entre les différentes positions sont nécessaires.

Comment fonctionne la distance de Hamming

Nous allons voir comment calculer la distance de Hamming à l'aide d'exemples, en commençant par de simples chaînes binaires et en passant à des applications plus complexes.

Exemple de chaîne binaire

L'application la plus simple de la distance de Hamming est la comparaison de chaînes binaires. Analysons deux chaînes de 8 bits :

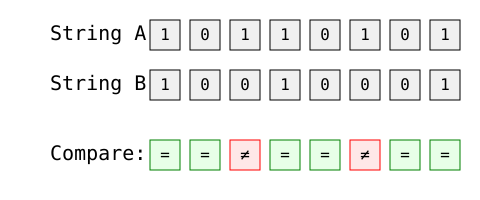
Image par l'auteur

Calcul étape par étape :

1. Position 1 : 1 = 1 (match)
2. Position 2 : 0 = 0 (match)
3. Position 3 : 1 ≠ 0 (différence)
4. Position 4 : 1 = 1 (match)
5. Position 5 : 0 = 0 (match)
6. Position 6 : 1 ≠ 0 (différence)
7. Position 7 : 0 = 0 (match)
8. Position 8 : 1 = 1 (match)

La distance de Hamming est de 2, car il y a deux positions où les cordes diffèrent (positions 3 et 6).

Exemple de séquence d'ADN

La distance de Hamming est fréquemment utilisée en bioinformatique pour comparer les séquences génétiques. Considérons deux fragments d'ADN :

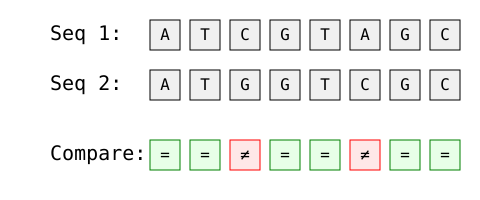
Image par l'auteur

Analyse étape par étape :

1. Les paires de bases correspondent aux positions 1, 2, 4, 5, 7 et 8.
2. Les différences se situent aux positions 3 (C→G) et 6 (A→C).
3. Distance de Hamming = 2 mutations

Cette comparaison aide les biologistes à quantifier les mutations génétiques et à analyser la similarité de l'ADN.

Exemple de chaîne de texte

La distance de Hamming fonctionne également avec des chaînes de texte normales de même longueur :

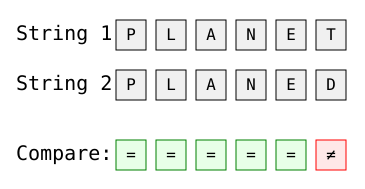
Image par l'auteur

La distance de Hamming est ici de 1, la seule différence se situant à la dernière position ("T" contre "D").

Ce type de comparaison est utile dans les cas suivants

• Systèmes de vérification orthographique
• Vérification OCR(reconnaissance optique de caractères)
• Analyse de la similarité des textes

Chaque exemple démontre que la distance de Hamming constitue un moyen simple et efficace de quantifier les différences entre les séquences, quel que soit le type de données comparées. L'idée maîtresse est qu'elle examine les différences entre les postes tout en ignorant la nature spécifique des changements.

Applications de la distance de Hamming

Détection et correction des erreurs

La distance de Hamming a jeté les bases des codes de détection et de correction d'erreurs dans les communications numériques. En ajoutant stratégiquement des bits de parité pour créer des distances minimales entre les mots de code valides, les systèmes peuvent détecter lorsque les données reçues ne correspondent pas à des modèles valides et même corriger les erreurs en les faisant correspondre au mot de code valide le plus proche. Ce principe est à la base de technologies modernes telles que la mémoire ECC (Error-Correcting Code) dans les ordinateurs, la correction d'erreurs des codes QR et les systèmes de communication dans l'espace lointain où l'intégrité des données est cruciale.

Théorie de l'information

La théorie de l'information utilise la distance de Hamming pour concevoir des systèmes de communication fiables. Lorsqu'ils créent des codes de traitement des erreurs, les ingénieurs veillent à ce que les messages valides (mots de code) diffèrent par un nombre minimum de bits. Par exemple, si les messages valides diffèrent toujours d'au moins deux bits, le système peut détecter si un seul bit est corrompu pendant la transmission. Si les messages valides diffèrent d'au moins trois bits, le système peut même corriger les erreurs d'un seul bit en identifiant le message valide le plus proche. Ces principes permettent de créer des systèmes de communication robustes utilisés dans tous les domaines, des communications par satellite au stockage de données.

Bioinformatique

Les chercheurs en génétique utilisent la distance de Hamming pour analyser les séquences d'ADN et quantifier les mutations. En comparant les séquences génétiques position par position, les scientifiques peuvent identifier les mutations ponctuelles, suivre les changements évolutifs et étudier la diversité génétique. Cette application s'avère particulièrement précieuse dans l'étude des mutations de maladies, où la compréhension des positions exactes des changements génétiques aide les chercheurs à suivre l'évolution des maladies et leur propagation au sein des populations.

Apprentissage automatique

Dans l'apprentissage automatique, la distance de Hamming sert de mesure de similarité pour les données binaires ou catégorielles. Il permet de comparer les vecteurs de caractéristiques dans les tâches de reconnaissance des formes, de mesurer la similarité dans les systèmes de recommandation et d'analyser les données catégorielles dans les problèmes de classification. La simplicité de la métrique et l'efficacité de son calcul la rendent particulièrement utile lorsque l'on travaille avec des données binaires de haute dimension ou lorsqu'il est nécessaire d'effectuer des calculs de similarité rapides pour de grands ensembles de données.

Propriétés mathématiques

Propriétés de l'espace métrique

La distance de Hamming forme un espace métrique mathématique, ce qui signifie qu'elle suit quatre règles fondamentales. Tout d'abord, la distance est toujours non négative - vous ne pouvez pas avoir un nombre négatif de positions où les chaînes diffèrent. Deuxièmement, la distance entre deux séquences est nulle si et seulement si elles sont identiques. Troisièmement, la distance présente une symétrie - comparer la séquence A à B donne le même résultat que comparer B à A. Enfin, elle satisfait à l'inégalité triangulaire : la distance entre les séquences A et C ne peut être supérieure à la somme des distances entre A et B et B et C.

Propriétés des chaînes binaires

Lorsque l'on travaille avec des chaînes binaires, la distance de Hamming présente des caractéristiques particulières qui la rendent particulièrement utile pour la détection des erreurs. Pour deux chaînes binaires de longueur n, leur distance de Hamming ne peut pas dépasser n, ne se produisant que lorsque les chaînes sont complémentaires l'une de l'autre. La probabilité d'une distance de Hamming spécifique "d" entre deux chaînes binaires aléatoires suit une distribution binomiale, la distance la plus probable étant n/2. Cette propriété permet de concevoir des codes de détection d'erreurs capables de reconnaître si des bits ont été retournés pendant la transmission.

Distance de Hamming en Python et R

Mise en œuvre de Python

Python propose à la fois des fonctions de bibliothèque intégrées et des implémentations personnalisées pour calculer la distance de Hamming. La bibliothèque SciPy offre la solution la plus efficace grâce à ses fonctions de distance spatiale :

from scipy.spatial.distance import hamming

# For working with strings
string1 = "1010101"
string2 = "1000101"

# Convert to list of integers for hamming function
arr1 = [int(bit) for bit in string1]
arr2 = [int(bit) for bit in string2]

# Calculate Hamming distance
distance = hamming(arr1, arr2) * len(arr1)  # Multiply by length because SciPy returns fraction
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

# For DNA sequences
sequence1 = "ATCGTACT"
sequence2 = "ATCGCACT"
distance = hamming(list(sequence1), list(sequence2)) * len(sequence1)
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

Pour ceux qui préfèrent une mise en œuvre personnalisée :

def hamming_distance(str1: str, str2: str) -> int:
    """Calculate Hamming distance between two strings."""
    if len(str1) != len(str2):
        raise ValueError("Strings must be of equal length")
    return sum(c1 != c2 for c1, c2 in zip(str1, str2))

# Example usage
print(hamming_distance("1010101", "1000101"))  # Output: 1

R mise en œuvre

R offre un moyen simple de calculer la distance de Hamming à l'aide de fonctions de base :

hamming_distance <- function(str1, str2) {
    if (nchar(str1) != nchar(str2)) {
        stop("Strings must be equal length")
    }
    sum(strsplit(str1, "")[[1]] != strsplit(str2, "")[[1]])
}

# Example usage
hamming_distance("1010101", "1000101")
# [1] 1

# For DNA sequences
hamming_distance("ATCGTACT", "ATCGCACT")
# [1] 1

Pour approfondir ces exemples de codage et explorer d'autres applications pratiques des mesures de distance, consultez ces ressources complètes :

• Conception de workflows d'apprentissage automatique en Python - Apprenez à mettre en œuvre des métriques de distance dans les pipelines d'apprentissage automatique et à les intégrer dans vos workflows de ML.
• Cluster Analysis in R - Découvrez comment appliquer des méthodes basées sur la distance pour une classification et un regroupement efficaces des données.

Ces cours vous aideront à aller au-delà des implémentations de base et à comprendre l'impact des mesures de distance sur les applications d'apprentissage automatique, quel que soit votre langage de programmation préféré.

Hamming vs. Autres approches

Image par l'auteur

Distance de Levenshtein (distance d'édition)

La distance de Levenshtein représente le nombre minimum de modifications d'un seul caractère nécessaires pour transformer une chaîne de caractères en une autre. Contrairement à la distance de Hamming, elle peut traiter des chaînes de différentes longueurs en tenant compte des insertions et des suppressions ainsi que des substitutions. Cette flexibilité le rend particulièrement utile pour les correcteurs orthographiques, l'alignement des séquences d'ADN et la correspondance de chaînes floues, bien que cette polyvalence se fasse au prix d'une plus grande complexité de calcul. Lors de la comparaison de chaînes de caractères telles que "planet" et "plan", la distance de Levenshtein compterait la suppression de "e" et de "t" comme deux opérations, alors que la distance de Hamming ne pourrait pas du tout effectuer cette comparaison.

Distance Damerau-Levenshtein

S'appuyant sur la distance standard de Levenshtein, la distance de Damerau-Levenshtein ajoute la transposition de caractères adjacents comme opération valide. Cet ajout le rend particulièrement efficace pour détecter les erreurs de frappe courantes où les caractères sont accidentellement intervertis. Par exemple, en comparant "form" à "from", il considère qu'il s'agit d'une seule transposition et non de deux substitutions distinctes. Cette métrique est largement utilisée dans les applications de traitement du langage naturel, en particulier dans les systèmes de correction automatique de l'orthographe où la transposition des caractères est une erreur de frappe courante.

Distance Jaro-Winkler

La distance de Jaro-Winkler adopte une approche unique en se concentrant sur la pondération de la position des caractères, favorisant particulièrement les correspondances au début des chaînes de caractères. Au lieu de compter les opérations d'édition, il produit un score de similarité entre 0 et 1, où 1 indique une correspondance parfaite. Cette métrique excelle dans la comparaison des noms propres et des chaînes courtes, ce qui la rend idéale pour les tâches de couplage et de dédoublonnage d'enregistrements. Par exemple, si vous comparez des noms tels que "Martha" et "Marhta", vous obtiendrez un score de similarité plus élevé car les caractères différents apparaissent plus loin dans la chaîne.

Choisir la bonne métrique de distance

Différents scénarios requièrent différentes mesures de distance. Tenez compte de ces facteurs clés lors du choix de votre approche :

Exigences en matière de vitesse et d'efficacité

• La distance de Hamming offre le calcul le plus rapide
• Levenshtein nécessite une plus grande puissance de traitement
• Jaro-Winkler se situe entre les deux en termes de vitesse

Considérations sur la longueur des chaînes de caractères

• Chaînes de longueur fixe (données binaires, codes de hachage) : Distance de Hamming
• Chaînes de longueur variable (entrée utilisateur, texte naturel) : Distance de Levenshtein
• Chaînes et noms courts : Jaro-Winkler distance

Types d'erreurs à traiter 

• Substitutions uniquement : Distance de Hamming 
• Opérations d'édition complètes : Distance de Levenshtein 
• Échange de personnages : Distance Damerau-Levenshtein 
• Variations de noms : Jaro-Winkler distance

Domaine d'application

• Communication numérique et détection des erreurs : Distance de Hamming
• Traitement de texte et vérification orthographique : Distance de Levenshtein
• Déduplication des bases de données et correspondance des enregistrements : Jaro-Winkler distance
• Traitement du langage naturel : Distance Damerau-Levenshtein

Cette comparaison structurée montre que chaque mesure de distance remplit des fonctions distinctes, la distance de Hamming étant particulièrement utile dans les scénarios où sa simplicité et sa rapidité correspondent aux exigences de comparaison de longueurs fixes.

Conclusion

L'élégance de la distance de Hamming réside dans sa simplicité. En comptant les positions où les séquences diffèrent, elle offre un moyen robuste de mesurer la dissimilarité, que ce soit pour détecter des erreurs dans des données transmises ou pour analyser des mutations génétiques. Cette mesure est particulièrement utile dans les domaines où chaque poste a la même importance et où les remplacements sont la principale préoccupation.

Lorsque vous explorerez les mesures de distance dans votre propre travail, considérez la distance de Hamming lorsque :

• Travailler avec des séquences de longueur fixe
• Traitement des données binaires ou catégorielles
• Construire des systèmes de détection d'erreurs
• Analyse des séquences génétiques
• Développement d'algorithmes de recherche de motifs

Pour continuer à développer votre expertise avec les métriques de distance et d'autres concepts fondamentaux de la science des données, explorez notre programme de certification Data Scientist, disponible en Python et en R.