Explicação da distância de Hamming: A teoria e os aplicativos

As métricas de distância fornecem maneiras essenciais de medir as diferenças entre os objetos. Enquanto métricas como a distância euclidiana ou de Manhattan medem as diferenças espaciais, a distância de Hamming adota uma abordagem diferente: Ele conta as posições em que duas sequências diferem. Isso o torna particularmente valioso para a detecção de erros, validação de dados e teoria da informação.

Originalmente desenvolvida por Richard Hamming em 1950, enquanto trabalhava em sistemas de verificação de código nos Laboratórios Bell, a distância de Hamming evoluiu para além de suas raízes nas telecomunicações. Atualmente, ele serve como uma métrica fundamental em diversos campos, incluindo:

• Validação de dados e verificação de integridade
• Análise de sequência de DNA em bioinformática
• Correspondência de padrões na recuperação de informações
• Comparação de recursos no machine learning

Neste guia, exploraremos como funciona a distância de Hamming, examinaremos suas aplicações práticas e a implementaremos em Python e R. Os conceitos e as implementações que abordaremos aumentarão sua capacidade de resolver problemas de validação de dados, bioinformática e machine learning.

O que é a distância de Hamming?

A distância de Hamming mede o número de posições em que duas cadeias de caracteres de igual comprimento têm símbolos diferentes. Pense nisso como a contagem do número mínimo de substituições necessárias para transformar uma string em outra.

Por exemplo, comparando duas cadeias de caracteres binárias:

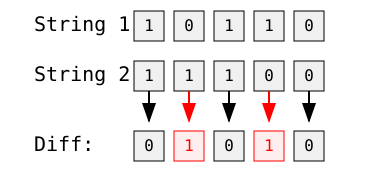
Imagem do autor

A distância de Hamming aqui é 2 porque as cadeias de caracteres diferem em duas posições - o segundo e o quarto bits.

Matematicamente, para duas cadeias de caracteres x e y de igual comprimento n, a distância de Hamming D(x,y) é expressa como:

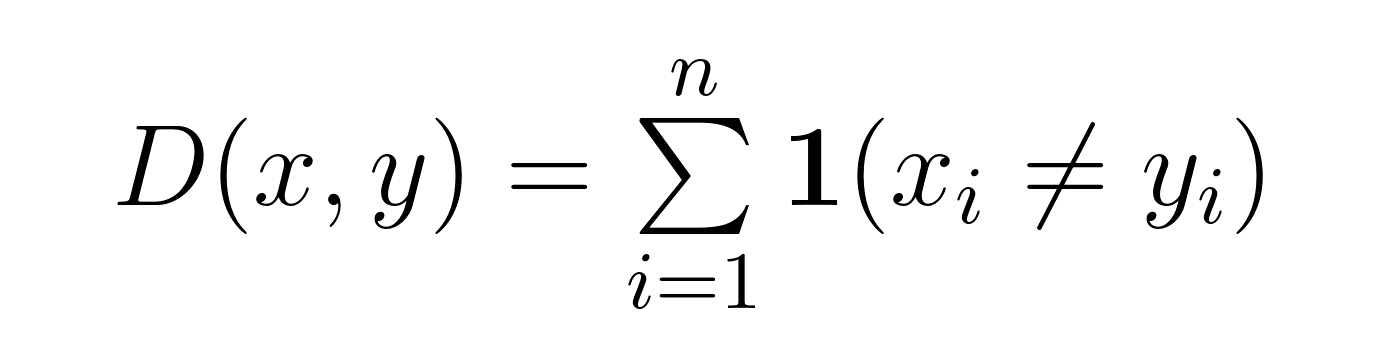
Essa fórmula conta as posições em que xᵢ ≠ yᵢ. Para cadeias de caracteres binárias, isso simplifica a contagem de onde os bits diferem. Para outros tipos de sequências (como DNA ou texto), ele conta as posições com símbolos diferentes.

Você deve estar ciente de duas propriedades importantes:

1. Ele requer cadeias de caracteres de igual comprimento.
2. Ele conta apenas as substituições, não as inserções ou exclusões.

Essas propriedades tornam a distância de Hamming ideal para cenários em que:

• Os dados consistem em códigos ou sequências de comprimento fixo.
• Somente os erros de substituição são importantes.
• São necessárias comparações rápidas e por posição.

Como funciona a distância de Hamming

Vamos explorar como calcular a distância de Hamming por meio de exemplos, começando com cadeias binárias simples e passando para aplicações mais complexas.

Exemplo de string binária

A aplicação mais direta da distância de Hamming é a comparação de strings binárias. Vamos analisar duas cadeias de caracteres de 8 bits:

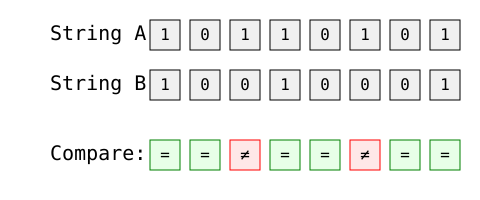
Imagem do autor

Cálculo passo a passo:

1. Posição 1: 1 = 1 (correspondência)
2. Posição 2: 0 = 0 (correspondência)
3. Posição 3: 1 ≠ 0 (diferença)
4. Posição 4: 1 = 1 (correspondência)
5. Posição 5: 0 = 0 (correspondência)
6. Posição 6: 1 ≠ 0 (diferença)
7. Posição 7: 0 = 0 (correspondência)
8. Posição 8: 1 = 1 (correspondência)

A distância de Hamming é 2, pois há duas posições em que as cadeias de caracteres são diferentes (posições 3 e 6).

Exemplo de sequência de DNA

A distância de Hamming é usada com frequência na bioinformática para comparar sequências genéticas. Considere dois fragmentos de DNA:

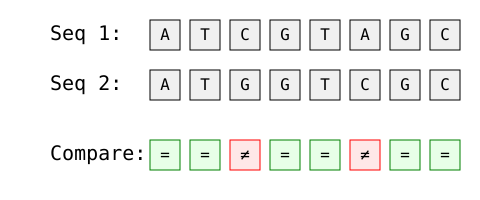
Imagem do autor

Análise passo a passo:

1. Os pares de bases coincidem nas posições 1, 2, 4, 5, 7 e 8
2. As diferenças ocorrem nas posições 3 (C→G) e 6 (A→C)
3. Distância de Hamming = 2 mutações

Essa comparação ajuda os biólogos a quantificar as mutações genéticas e analisar a similaridade do DNA.

Exemplo de string de texto

A distância de Hamming também funciona com sequências de texto regulares de igual comprimento:

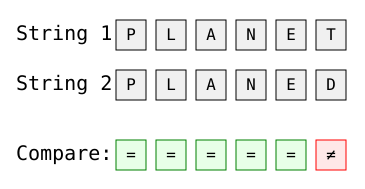
Imagem do autor

A distância de Hamming aqui é 1, com a única diferença na última posição ('T' vs. 'D').

Esse tipo de comparação é útil para você:

• Sistemas de verificação ortográfica
• Verificação de OCR(reconhecimento óptico de caracteres)
• Análise de similaridade de texto

Cada exemplo demonstra como a distância de Hamming oferece uma maneira simples, porém eficaz, de quantificar as diferenças entre as sequências, independentemente do tipo de dados que estão sendo comparados. A principal percepção é que ele analisa as diferenças por posição, ignorando a natureza específica das mudanças.

Aplicações da distância de Hamming

Detecção e correção de erros

A distância de Hamming estabeleceu a base para códigos de detecção e correção de erros em comunicações digitais. Ao adicionar estrategicamente bits de paridade para criar distâncias mínimas entre palavras-código válidas, os sistemas podem detectar quando os dados recebidos não correspondem a padrões válidos e até mesmo corrigir erros mapeando para a palavra-código válida mais próxima. Esse princípio impulsiona as tecnologias modernas, como a memória ECC (Código de Correção de Erros) em computadores, a correção de erros de código QR e os sistemas de comunicação espacial profunda, em que a integridade dos dados é fundamental.

Teoria da informação

A teoria da informação usa a distância de Hamming para projetar sistemas de comunicação confiáveis. Ao criar códigos de tratamento de erros, os engenheiros garantem que as mensagens válidas (palavras de código) diferem em um número mínimo específico de bits. Por exemplo, se as mensagens válidas sempre diferem em pelo menos dois bits, o sistema pode detectar quando um único bit é corrompido durante a transmissão. Se as mensagens válidas diferirem em pelo menos três bits, o sistema poderá até mesmo corrigir erros de um único bit identificando a mensagem válida mais próxima. Esses princípios ajudam a criar sistemas de comunicação robustos usados em tudo, desde comunicações via satélite até armazenamento de dados.

Bioinformática

Os pesquisadores de genética usam a distância de Hamming para analisar sequências de DNA e quantificar mutações. Ao comparar as sequências genéticas posição por posição, os cientistas podem identificar mutações pontuais, rastrear mudanças evolutivas e estudar a diversidade genética. Esse aplicativo se mostra particularmente valioso no estudo de mutações de doenças, em que a compreensão das posições exatas das alterações genéticas ajuda os pesquisadores a rastrear como as doenças evoluem e se espalham pelas populações.

Machine learning

No machine learning, a distância de Hamming serve como uma métrica de similaridade para dados binários ou categóricos. Ele ajuda a comparar vetores de recursos em tarefas de reconhecimento de padrões, medir a similaridade em sistemas de recomendação e analisar dados categóricos em problemas de classificação. A simplicidade e a eficiência do cálculo da métrica a tornam particularmente valiosa ao trabalhar com dados binários de alta dimensão ou quando são necessários cálculos rápidos de similaridade para grandes conjuntos de dados.

Propriedades matemáticas

Propriedades do espaço métrico

A distância de Hamming forma um espaço métrico matemático, o que significa que ela segue quatro regras fundamentais. Primeiro, a distância é sempre não negativa - você não pode ter um número negativo de posições em que as cadeias de caracteres sejam diferentes. Segundo, a distância entre duas sequências é zero se e somente se elas forem idênticas. Em terceiro lugar, a distância apresenta simetria - a comparação da sequência A com B dá o mesmo resultado que a comparação de B com A. Por fim, ela satisfaz a desigualdade triangular: a distância entre as sequências A e C não pode ser maior que a soma das distâncias de A para B e de B para C.

Propriedades da cadeia binária

Ao trabalhar com cadeias binárias, a distância de Hamming assume características especiais que a tornam particularmente útil para a detecção de erros. Para quaisquer duas cadeias binárias de comprimento n, sua distância de Hamming não pode exceder n, ocorrendo somente quando as cadeias são complementos uma da outra. A probabilidade de uma distância de Hamming específica "d" entre duas cadeias binárias aleatórias segue uma distribuição binomial, com a distância mais provável sendo n/2. Essa propriedade ajuda a projetar códigos de detecção de erros que podem reconhecer quando os bits foram invertidos durante a transmissão.

Distância de Hamming em Python e R

Implementação do Python

O Python oferece funções de biblioteca integradas e implementações personalizadas para que você calcule a distância de Hamming. A biblioteca SciPy oferece a solução mais eficiente por meio de suas funções de distância espacial:

from scipy.spatial.distance import hamming

# For working with strings
string1 = "1010101"
string2 = "1000101"

# Convert to list of integers for hamming function
arr1 = [int(bit) for bit in string1]
arr2 = [int(bit) for bit in string2]

# Calculate Hamming distance
distance = hamming(arr1, arr2) * len(arr1)  # Multiply by length because SciPy returns fraction
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

# For DNA sequences
sequence1 = "ATCGTACT"
sequence2 = "ATCGCACT"
distance = hamming(list(sequence1), list(sequence2)) * len(sequence1)
print(f"Hamming distance: {int(distance)}")  # Output: Hamming distance: 1

Para aqueles que preferem uma implementação personalizada:

def hamming_distance(str1: str, str2: str) -> int:
    """Calculate Hamming distance between two strings."""
    if len(str1) != len(str2):
        raise ValueError("Strings must be of equal length")
    return sum(c1 != c2 for c1, c2 in zip(str1, str2))

# Example usage
print(hamming_distance("1010101", "1000101"))  # Output: 1

Implementação da R

O R oferece uma maneira simples de calcular a distância de Hamming usando funções básicas:

hamming_distance <- function(str1, str2) {
    if (nchar(str1) != nchar(str2)) {
        stop("Strings must be equal length")
    }
    sum(strsplit(str1, "")[[1]] != strsplit(str2, "")[[1]])
}

# Example usage
hamming_distance("1010101", "1000101")
# [1] 1

# For DNA sequences
hamming_distance("ATCGTACT", "ATCGCACT")
# [1] 1

Para se basear nesses exemplos de codificação e explorar mais aplicações de métricas de distância na prática, confira estes recursos abrangentes:

• Projetando fluxos de trabalho de aprendizado de máquina em Python - Aprenda a implementar métricas de distância em pipelines de machine learning e a integrá-las aos seus fluxos de trabalho de ML
• Análise de clusters em R - Descubra como aplicar métodos baseados em distância para agrupamento e classificação eficazes de dados

Esses cursos ajudarão você a ir além das implementações básicas para entender como as métricas de distância afetam os aplicativos de machine learning, independentemente da sua linguagem de programação preferida.

Hamming vs. Outras abordagens

Imagem do autor

Distância de Levenshtein (distância de edição)

A distância de Levenshtein representa o número mínimo de edições de um único caractere necessárias para transformar uma string em outra. Ao contrário da distância de Hamming, ela pode lidar com cadeias de caracteres de diferentes comprimentos, considerando inserções e exclusões juntamente com substituições. Essa flexibilidade o torna particularmente valioso para corretores ortográficos, alinhamento de sequências de DNA e correspondência de sequências difusas, embora essa versatilidade tenha o custo de uma maior complexidade computacional. Ao comparar cadeias de caracteres como "planet" e "plan", a distância de Levenshtein contaria a exclusão de 'e' e 't' como duas operações, enquanto a distância de Hamming não poderia fazer essa comparação.

Distância Damerau-Levenshtein

Com base na distância padrão de Levenshtein, a distância Damerau-Levenshtein acrescenta a transposição de caracteres adjacentes como uma operação válida. Esse acréscimo o torna especialmente eficaz na detecção de erros comuns de digitação em que os caracteres são acidentalmente trocados. Por exemplo, ao comparar "form" com "from", isso seria considerado uma única transposição em vez de duas substituições separadas. Essa métrica foi amplamente utilizada em aplicativos de processamento de linguagem natural, especialmente em sistemas automatizados de correção ortográfica, em que a transposição de caracteres é um erro comum de digitação.

Distância Jaro-Winkler

A distância Jaro-Winkler adota uma abordagem exclusiva, concentrando-se nos pesos da posição do caractere, favorecendo particularmente as correspondências no início das cadeias de caracteres. Em vez de contar as operações de edição, ele produz uma pontuação de similaridade entre 0 e 1, em que 1 indica uma correspondência perfeita. Essa métrica é excelente na comparação de nomes próprios e cadeias curtas, o que a torna ideal para tarefas de vinculação de registros e deduplicação. Por exemplo, ao comparar nomes como "Martha" e "Marhta", ele atribuiria uma pontuação de similaridade mais alta porque os caracteres diferentes aparecem mais tarde na cadeia de caracteres.

Escolhendo a métrica de distância correta

Cenários diferentes exigem métricas de distância diferentes. Considere estes fatores-chave ao selecionar sua abordagem:

Requisitos de velocidade e eficiência

• A distância de Hamming oferece o cálculo mais rápido
• Levenshtein requer mais poder de processamento
• Jaro-Winkler fica entre os dois em termos de velocidade

Considerações sobre o comprimento da cadeia de caracteres

• Cadeias de caracteres de comprimento fixo (dados binários, códigos de hash): Distância de Hamming
• Cadeias de caracteres de comprimento variável (entrada do usuário, texto natural): Distância de Levenshtein
• Cadeias de caracteres e nomes curtos: Distância Jaro-Winkler

Tipos de erro a serem tratados 

• Somente substituições: Distância de Hamming 
• Operações de edição completa: Distância de Levenshtein 
• Troca de personagens: Distância Damerau-Levenshtein 
• Variações do nome: Distância Jaro-Winkler

Domínio do aplicativo

• Comunicação digital e detecção de erros: Distância de Hamming
• Processamento de texto e verificação ortográfica: Distância de Levenshtein
• Desduplicação de banco de dados e correspondência de registros: Distância Jaro-Winkler
• Processamento de linguagem natural: Distância Damerau-Levenshtein

Essa comparação estruturada mostra como cada métrica de distância serve a propósitos distintos, sendo a distância de Hamming particularmente valiosa em cenários em que sua simplicidade e velocidade se alinham aos requisitos de comparação de comprimento fixo.

Conclusão

A elegância da distância de Hamming está em sua simplicidade. Ao contar as posições em que as sequências diferem, ele fornece uma maneira robusta de medir a dissimilaridade, quer você esteja detectando erros em dados transmitidos ou analisando mutações genéticas. Essa métrica é particularmente brilhante em domínios em que cada posição é igualmente importante e as substituições são a principal preocupação.

À medida que você explorar as métricas de distância em seu próprio trabalho, considere a distância de Hamming quando:

• Trabalhar com sequências de comprimento fixo
• Lidar com dados binários ou categóricos
• Criação de sistemas de detecção de erros
• Análise de sequências genéticas
• Desenvolvimento de algoritmos de correspondência de padrões

Para continuar a desenvolver sua experiência com métricas de distância e outros conceitos fundamentais de ciência de dados, explore nosso programa de Certificação de Cientista de Dados, disponível em Python e R.