Redes de Kolmogorov-Arnold (KAN): Guía de aplicación

¿Qué son las redes de Kolmogorov-Arnold (KAN)?

Las Redes de Kolmogorov-Arnold (KAN) se basan en el teorema de representación de Kolmogorov-Arnold, que les sirve de fundamento matemático. El teorema afirma que cualquier función continua multivariable puede descomponerse en una suma de funciones más sencillas de una sola variable.

Sin embargo, aunque el teorema garantiza que estas funciones univariantes existen, no nos dice cómo encontrarlas. Aquí es donde entran en juego las KAN.

En lugar de aproximar directamente toda una función compleja, como hacen la mayoría de los demás modelos, los KAN se centran en aprender estas funciones univariantes más sencillas. Este enfoque da como resultado un modelo que no sólo es flexible, sino también muy interpretable, sobre todo cuando se trata de relaciones no lineales en los datos.

Redes de Kolmogorov-Arnold (KAN) vs. Redes de Kolmogorov-Arnold (KAN) vs. Redes de Kolmogorov-Arnold. Perceptrones multicapa (MLP)

La principal diferencia entre las KAN y los Perceptrones Multicapa (MLP) tradicionales radica en cómo se produce el aprendizaje.

En los MLP, las neuronas se activan mediante funciones fijas como ReLU o sigmoide, y estas activaciones se pasan a través de matrices de pesos lineales. En cambio, las KAN colocan funciones de activación aprendibles en los bordes (conexiones) entre neuronas, en lugar de en las neuronas mismas. En la implementación original, estas funciones están parametrizadas como B-splines, aunque los autores mencionan que también se pueden utilizar otros tipos de funciones, como los polinomios de Chebyshev, dependiendo del problema.

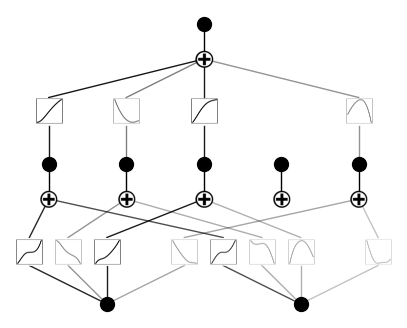
Tanto las KAN superficiales como las profundas descomponen las funciones complejas en una serie de funciones univariantes más sencillas. La figura siguiente pone de manifiesto esta diferencia de arquitectura: Los MLP utilizan activaciones fijas dentro de las neuronas, mientras que los KAN implementan funciones aprendibles a lo largo de las aristas y las suman en los nodos. Este cambio arquitectónico permite a las KAN adaptarse dinámicamente a los datos, consiguiendo potencialmente una mayor precisión con menos parámetros que los MLP. Además, tras el entrenamiento, el modelo puede hacerse más pequeño si no se utilizan todas las aristas para la aproximación.

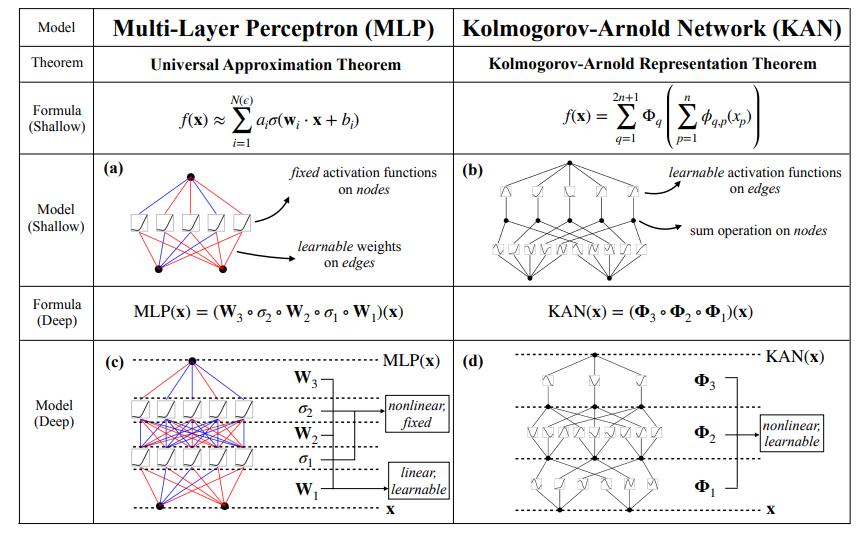
Fuente: Liu et al., 2024

Además, tras el entrenamiento, los KAN nos permiten extraer las funciones univariables aprendidas, lo que hace posible reconstruir la función multivariable resultante. Esta característica es especialmente útil cuando la interpretabilidad es crucial. Mostraremos este proceso en la sección de ejemplos más adelante.

pip install git+https://github.com/KindXiaoming/pykan.git

Utilización

Tras instalar pykan, podemos empezar a importar los módulos necesarios y definir un KAN sencillo:

from kan import *
model = KAN(width=[2,5,1])

Aquí, especificamos las dimensiones del modelo en el parámetro width. En este caso concreto, estamos haciendo un modelo con 2 entradas, 1 salida y una capa de 5 neuronas ocultas.Ahora, vamos a crear un conjunto de datos para nuestro experimento. Utilizaré un polinomio aleatorio de 2 variables que se me acaba de ocurrir sobre la marcha:

from kan.utils import create_dataset
f = lambda x: 3*x[:,[0]]**3+2*x[:,[0]]+4 + 2 * x[:,[0]] * x[:,[1]] ** 2 + 3 * x[:,[1]] ** 3
dataset = create_dataset(f, n_var=2)

Aquí utilizo una función lambda para definir un polinomio. La biblioteca parece utilizar la biblioteca numpy bajo el capó, de ahí la sintaxis. Ahora podemos cargar el conjunto de datos en un modelo y visualizarlo:

model(dataset['train_input']);
model.plot()

Éste es el aspecto del resultado:

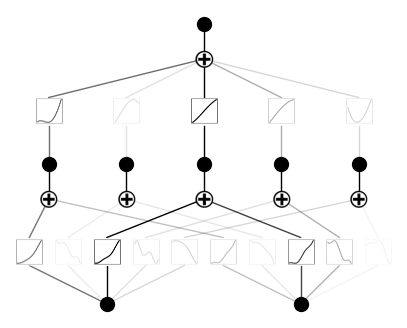
Formación

Para ejecutar el entrenamiento, necesitamos utilizar el método .fit():

model.fit(dataset, steps=1000);

Después de la formación, éste es el aspecto de nuestra KAN:

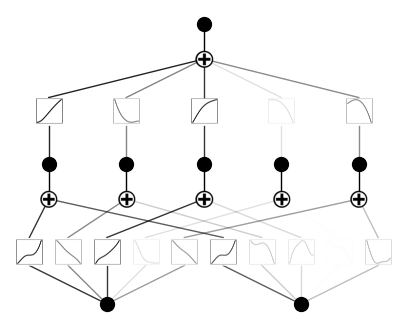
Ahora, vamos a podar y trazar de nuevo el modelo:

model = model.prune()
model.plot()

Éste es el aspecto actual del modelo. Como puedes ver, hemos podado una función de activación:

Esto tiene sentido, porque nuestro polinomio no utiliza cinco combinaciones diferentes de potencias de variables de entrada.

Casos de uso de las KAN

Las redes de Kolmogorov-Arnold (KAN) se han mostrado prometedoras en diversos campos debido a su capacidad para modelar relaciones complejas y no lineales con menos parámetros que las redes neuronales tradicionales. He aquí algunos casos de uso clave:

• Modelización científica y ajuste de datos: Las KAN son especialmente eficaces para los problemas científicos que requieren un modelado preciso de funciones complejas. Como las KAN aproximan funciones multivariables aprendiendo otras univariables más sencillas, pueden captar eficazmente patrones intrincados en los datos científicos. Para tareas como el ajuste de curvas, los KAN suelen superar a los MLP tradicionales gracias a su arquitectura flexible.
• Resolución de ecuaciones diferenciales parciales (EDP): Las KAN han demostrado un gran potencial en la resolución de EDP, que se utilizan habitualmente en física e ingeniería para modelizar procesos como la transferencia de calor y la dinámica de fluidos. Su capacidad para manejar problemas no lineales de alta dimensión los hace especialmente útiles en este ámbito, superando a los MLP en precisión e interpretabilidad.
• Regresión simbólica: Las KAN destacan en la regresión simbólica, donde el objetivo es descubrir las expresiones matemáticas que mejor describen un conjunto de datos. Su capacidad para aprender estructuras compositivas las convierte en una herramienta ideal para redescubrir leyes físicas y matemáticas directamente a partir de los datos.

Ventajas y desventajas de las KAN

Exploremos algunas de las formas en que las KAN mejoran las limitaciones de las redes neuronales convencionales:

• Interpretabilidad: A diferencia de los modelos tradicionales de aprendizaje profundo, los KAN proporcionan una estructura más interpretable. Las funciones aprendibles pueden visualizarse y analizarse, ofreciendo información sobre el proceso de toma de decisiones del modelo. Esta característica es especialmente valiosa en los campos científicos, donde comprender el funcionamiento del modelo es tan crucial como lograr una gran precisión.
• Flexibilidad: Las KAN no se limitan a un único tipo de función de activación. Aunque suelen utilizar B-splines, pueden emplearse otras funciones de base, como los polinomios de Chebyshev, en función de la tarea específica. Esta flexibilidad hace que la arquitectura sea versátil y adaptable a diversas aplicaciones.

Las KAN presentan un nuevo y prometedor enfoque del aprendizaje profundo, pero como cualquier tecnología, vienen con sus propias debilidades:

• Complejidad computacional: Uno de los retos de las KAN es su intensidad computacional durante la fase de entrenamiento. Como los KAN utilizan funciones de activación aprendibles en los bordes, la complejidad de la evaluación de estas funciones puede ralentizar considerablemente el proceso de entrenamiento en comparación con los MLP tradicionales. Esta complejidad se amplifica aún más en tareas que requieren arquitecturas KAN profundas o funciones base muy detalladas.
• Necesidad de experiencia: Implementar y ajustar las KAN puede ser más complejo que trabajar con MLP tradicionales. La selección de las funciones de base adecuadas (por ejemplo, B-splines, polinomios de Chebyshev) y la configuración del modelo para una tarea específica requieren una comprensión matemática más profunda y una mayor interacción entre el ser humano y el modelo. Esto puede hacer que las KAN sean menos accesibles para los profesionales sin conocimientos especializados.

Interacción Humano-KAN

Un aspecto único de las Redes de Kolmogorov-Arnold (KAN) es su capacidad para facilitar una interacción significativa entre el modelo y la intuición humana. El artículo original describe cómo los investigadores pueden participar en el aprendizaje del modelo de formas que no son posibles con las redes neuronales tradicionales.

Tras entrenar una KAN en un problema concreto, los investigadores pueden extraer las funciones univariantes aprendidas que el modelo utiliza para aproximar la función multivariable compleja. Al estudiar estas funciones aprendidas, los investigadores obtienen información sobre las relaciones subyacentes en los datos.

Además, los conocimientos obtenidos de esta interacción permiten un perfeccionamiento iterativo. Los investigadores pueden ajustar la arquitectura del KAN, modificar los tipos de funciones de base (por ejemplo, pasar de B-splines a polinomios de Chebyshev) o ajustar el proceso de entrenamiento basándose en las funciones extraídas. Este enfoque humano en el bucle permite un proceso de modelado a medida, lo que hace que las KAN sean adaptables a distintos problemas científicos o matemáticos.

De este modo, las KAN facilitan una interacción bidireccional: aprenden de los datos para formar funciones complejas, y los humanos pueden guiar e interpretar este aprendizaje para perfeccionar el modelo o incluso descubrir nuevos conocimientos. Esta interacción es lo que hace que las KAN destaquen, transformando el aprendizaje automático en un esfuerzo más colaborativo y exploratorio.

Conclusión

En general, las Redes de Kolmogorov-Arnold (KAN) representan un avance emocionante y prometedor en la arquitectura de las redes neuronales. Su diseño único ofrece una alternativa flexible e interpretable a los MLP, con potencial para superar a los modelos tradicionales en diversas tareas.

A medida que la comunidad siga explorando las KAN mediante colaboraciones de código abierto y diversas aplicaciones, estas redes y sus extensiones podrían evolucionar hasta convertirse en potentes herramientas de última generación.