Kolmogorow-Arnold-Netzwerke (KANs): Ein Leitfaden mit Umsetzung

Was sind Kolmogorow-Arnold-Netzwerke (KANs)?

Kolmogorov-Arnold-Netzwerke (KANs) basieren auf dem Kolmogorov-Arnold-Repräsentationstheorem, das als mathematische Grundlage dient. Das Theorem besagt, dass jede kontinuierliche, multivariable Funktion in eine Summe von einfacheren, einvariablen Funktionen zerlegt werden kann.

Das Theorem garantiert zwar, dass diese univariaten Funktionen existieren, aber es sagt uns nicht, wie wir sie finden können. An dieser Stelle kommen die KANs ins Spiel.

Anstatt direkt eine ganze komplexe Funktion zu approximieren, wie es die meisten anderen Modelle tun, konzentrieren sich KANs auf das Lernen dieser einfacheren univariaten Funktionen. Dieser Ansatz führt zu einem Modell, das nicht nur flexibel, sondern auch sehr gut interpretierbar ist, insbesondere wenn es um nichtlineare Beziehungen in den Daten geht.

Kolmogorov-Arnold-Netzwerke (KANs) vs. Mehrschichtige Perceptrons (MLPs)

Der Hauptunterschied zwischen KANs und herkömmlichen Multi-Layer Perceptrons (MLPs) liegt in der Art und Weise, wie das Lernen erfolgt.

Bei MLPs werden die Neuronen mit festen Funktionen wie ReLU oder Sigmoid aktiviert, und diese Aktivierungen werden durch lineare Gewichtsmatrizen geleitet. Im Gegensatz dazu platzieren KANs lernbare Aktivierungsfunktionen an den Kanten (Verbindungen) zwischen den Neuronen und nicht an den Neuronen selbst. In der Originalimplementierung sind diese Funktionen als B-Splines parametrisiert, obwohl die Autoren erwähnen, dass je nach Problemstellung auch andere Arten von Funktionen, wie Tschebyscheff-Polynome, verwendet werden können.

Sowohl flache als auch tiefe KANs zerlegen komplexe Funktionen in eine Reihe von einfacheren, univariaten Funktionen. Die folgende Abbildung verdeutlicht diesen Unterschied in der Architektur: MLPs verwenden feste Aktivierungen innerhalb der Neuronen, während KANs lernbare Funktionen entlang der Kanten implementieren und diese auf den Knoten summieren. Durch diese architektonische Veränderung können sich KANs dynamisch an die Daten anpassen und mit weniger Parametern eine höhere Genauigkeit erreichen als MLPs. Außerdem kann das Modell nach dem Training verkleinert werden, wenn nicht alle Kanten zur Annäherung verwendet werden.

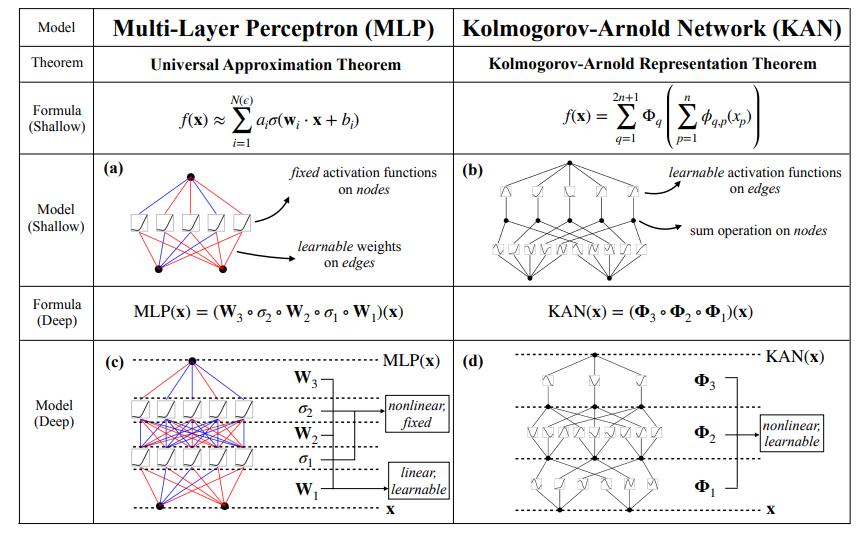
Quelle: Liu et al., 2024

Außerdem können wir mit KANs nach dem Training die gelernten univariaten Funktionen extrahieren und so die resultierende multivariable Funktion rekonstruieren. Diese Funktion ist besonders nützlich, wenn die Interpretierbarkeit entscheidend ist. Wir werden diesen Prozess später in den Beispielen erläutern.

pip install git+https://github.com/KindXiaoming/pykan.git

Verwendung

Nachdem wir pykan installiert haben, können wir damit beginnen, die notwendigen Module zu importieren und ein einfaches KAN zu definieren:

from kan import *
model = KAN(width=[2,5,1])

Hier geben wir die Dimensionen des Modells in dem Parameter width an. In diesem Fall erstellen wir ein Modell mit 2 Eingängen, 1 Ausgang und einer Schicht mit 5 versteckten Neuronen.Erstellen wir nun einen Datensatz für unser Experiment. Ich werde ein zufälliges Polynom mit zwei Variablen verwenden, das ich mir gerade ausgedacht habe:

from kan.utils import create_dataset
f = lambda x: 3*x[:,[0]]**3+2*x[:,[0]]+4 + 2 * x[:,[0]] * x[:,[1]] ** 2 + 3 * x[:,[1]] ** 3
dataset = create_dataset(f, n_var=2)

Hier verwende ich eine Lambda-Funktion, um ein Polynom zu definieren. Die Bibliothek scheint die numpy Bibliothek unter der Haube zu verwenden - daher die Syntax. Jetzt können wir den Datensatz in ein Modell laden und ihn visualisieren:

model(dataset['train_input']);
model.plot()

So sieht die Ausgabe aus:

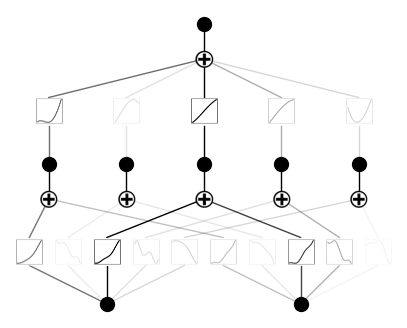
Ausbildung

Um ein Training durchzuführen, müssen wir die Methode .fit() verwenden:

model.fit(dataset, steps=1000);

Nach der Schulung sieht unsere KAN so aus:

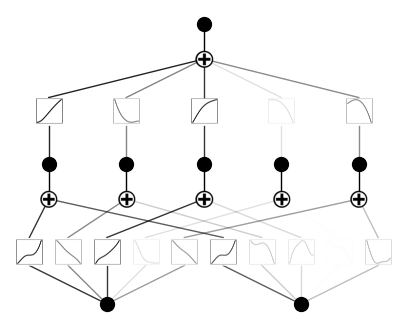
Jetzt beschneiden wir das Modell und zeichnen es erneut auf:

model = model.prune()
model.plot()

So sieht das Modell jetzt aus. Wie du siehst, haben wir eine Aktivierungsfunktion gestrichen:

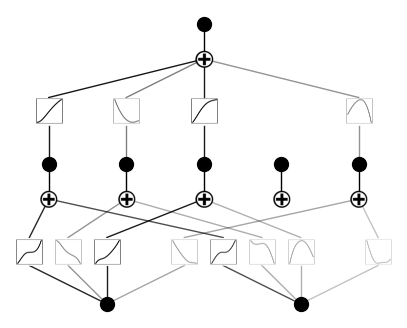
Das macht Sinn, weil unser Polynom nicht fünf verschiedene Kombinationen von Potenzen der Eingangsvariablen verwendet.

Anwendungsfälle von KANs

Kolmogorov-Arnold-Netzwerke (KANs) haben sich in verschiedenen Bereichen als vielversprechend erwiesen, da sie komplexe, nicht-lineare Beziehungen mit weniger Parametern modellieren können als herkömmliche neuronale Netze. Hier sind einige wichtige Anwendungsfälle:

• Wissenschaftliche Modellierung und Datenanpassung: KANs sind besonders effektiv für wissenschaftliche Probleme, die eine genaue Modellierung von komplexen Funktionen erfordern. Da KANs multivariable Funktionen durch das Lernen von einfacheren univariaten Funktionen approximieren, können sie komplexe Muster in wissenschaftlichen Daten effizient erfassen. Bei Aufgaben wie der Kurvenanpassung sind KANs aufgrund ihrer flexiblen Architektur oft besser als traditionelle MLPs.
• Lösen von partiellen Differentialgleichungen (PDEs): KANs haben ihr großes Potenzial bei der Lösung von PDEs bewiesen, die in der Physik und im Ingenieurwesen häufig zur Modellierung von Prozessen wie Wärmeübertragung und Flüssigkeitsdynamik verwendet werden. Ihre Fähigkeit, hochdimensionale, nichtlineare Probleme zu bewältigen, macht sie in diesem Bereich besonders nützlich und übertrifft MLPs an Genauigkeit und Interpretierbarkeit.
• Symbolische Regression: KANs eignen sich hervorragend für symbolische Regressionen, bei denen es darum geht, mathematische Ausdrücke zu finden, die einen Datensatz am besten beschreiben. Ihre Fähigkeit, kompositorische Strukturen zu erlernen, macht sie zu einem idealen Werkzeug, um physikalische und mathematische Gesetze direkt aus Daten wiederzuentdecken.

Vorteile und Nachteile von KANs

Wir wollen einige der Möglichkeiten erkunden, wie KANs die Einschränkungen herkömmlicher neuronaler Netze verbessern:

• Interpretierbarkeit: Im Gegensatz zu traditionellen Deep-Learning-Modellen bieten KANs eine besser interpretierbare Struktur. Die erlernbaren Funktionen können visualisiert und analysiert werden und bieten Einblicke in den Entscheidungsprozess des Modells. Diese Eigenschaft ist besonders in wissenschaftlichen Bereichen wertvoll, wo das Verständnis der Funktionsweise des Modells ebenso wichtig ist wie eine hohe Genauigkeit.
• Flexibilität: KANs sind nicht auf einen einzigen Typ von Aktivierungsfunktion beschränkt. Häufig werden B-Splines verwendet, aber je nach Aufgabenstellung können auch andere Basisfunktionen wie Tschebyscheff-Polynome eingesetzt werden. Diese Flexibilität macht die Architektur vielseitig und anpassungsfähig an eine Reihe von Anwendungen.

KANs sind ein vielversprechender neuer Ansatz für Deep Learning, aber wie jede Technologie haben auch sie ihre Schwächen:

• Computerkomplexität: Eine der Herausforderungen bei KANs ist ihre Rechenintensität während der Trainingsphase. Da KANs lernfähige Aktivierungsfunktionen an den Kanten verwenden, kann die Komplexität der Auswertung dieser Funktionen den Trainingsprozess im Vergleich zu traditionellen MLPs erheblich verlangsamen. Diese Komplexität wird bei Aufgaben, die tiefe KAN-Architekturen oder sehr detaillierte Basisfunktionen erfordern, noch verstärkt.
• Bedarf an Fachwissen: Die Implementierung und Abstimmung von KANs kann komplexer sein als die Arbeit mit traditionellen MLPs. Die Auswahl der geeigneten Basisfunktionen (z. B. B-Splines, Tschebyscheff-Polynome) und die Konfiguration des Modells für eine bestimmte Aufgabe erfordern ein tieferes mathematisches Verständnis und mehr Interaktion zwischen Mensch und Modell. Das kann dazu führen, dass KANs für Praktiker/innen ohne Spezialwissen weniger zugänglich sind.

Mensch-KAN-Interaktion

Ein einzigartiger Aspekt von Kolmogorov-Arnold-Netzwerken (KANs) ist ihre Fähigkeit, eine sinnvolle Interaktion zwischen dem Modell und der menschlichen Intuition zu ermöglichen. In der Originalarbeit wird beschrieben, wie Forscherinnen und Forscher das Lernen des Modells auf eine Weise beeinflussen können, die mit herkömmlichen neuronalen Netzen nicht möglich ist.

Nachdem ein KAN für ein bestimmtes Problem trainiert wurde, können Forscher die gelernten univariaten Funktionen extrahieren, die das Modell zur Annäherung an die komplexe multivariable Funktion verwendet. Durch die Untersuchung dieser gelernten Funktionen erhalten die Forscher Einblicke in die zugrunde liegenden Beziehungen in den Daten.

Außerdem ermöglichen die aus dieser Interaktion gewonnenen Erkenntnisse eine iterative Weiterentwicklung. Forscherinnen und Forscher können die Architektur des KAN optimieren, die Art der Basisfunktionen ändern (z. B. von B-Splines zu Tschebyscheff-Polynomen wechseln) oder den Trainingsprozess auf der Grundlage der extrahierten Funktionen anpassen. Dieser "Human-in-the-Loop"-Ansatz ermöglicht einen maßgeschneiderten Modellierungsprozess, der die KANs an verschiedene wissenschaftliche oder mathematische Probleme anpassbar macht.

Auf diese Weise ermöglichen KANs eine wechselseitige Interaktion: Sie lernen aus Daten, um komplexe Funktionen zu bilden, und Menschen können dieses Lernen anleiten und interpretieren, um das Modell zu verfeinern oder sogar neues Wissen zu entdecken. Dieses Zusammenspiel ist es, was die KANs auszeichnet und das maschinelle Lernen zu einem kollaborativen und explorativen Unterfangen macht.

Fazit

Insgesamt stellen Kolmogorov-Arnold-Netzwerke (KANs) einen spannenden und vielversprechenden Fortschritt in der Architektur neuronaler Netzwerke dar. Ihr einzigartiges Design bietet eine flexible und interpretierbare Alternative zu MLPs, die das Potenzial hat, traditionelle Modelle bei verschiedenen Aufgaben zu übertreffen.

Wenn die Community die KANs durch Open-Source-Kooperationen und verschiedene Anwendungen weiter erforscht, könnten sich diese Netzwerke und ihre Erweiterungen zu leistungsstarken, hochmodernen Tools entwickeln.