Redes Kolmogorov-Arnold (KANs): Um guia com implementação

O que são redes de Kolmogorov-Arnold (KANs)?

As redes de Kolmogorov-Arnold (KANs) são baseadas no teorema de representação de Kolmogorov-Arnold, que serve como base matemática. O teorema afirma que qualquer função contínua multivariável pode ser decomposta em uma soma de funções mais simples, de variável única.

Entretanto, embora o teorema garanta que essas funções univariadas existam, ele não nos diz como encontrá-las. É nesse ponto que os KANs entram em ação.

Em vez de aproximar diretamente uma função complexa inteira, como faz a maioria dos outros modelos, os KANs se concentram no aprendizado dessas funções univariadas mais simples. Essa abordagem resulta em um modelo que não é apenas flexível, mas também altamente interpretável, especialmente ao lidar com relações não lineares nos dados.

Redes de Kolmogorov-Arnold (KANs) vs. Redes de Kolmogorov-Arnold. Perceptrons de várias camadas (MLPs)

A principal diferença entre os KANs e os MLPs (Multi-Layer Perceptrons, perceptrons de várias camadas) tradicionais está na forma como o aprendizado ocorre.

Nas MLPs, os neurônios são ativados usando funções fixas como ReLU ou sigmoide, e essas ativações são passadas por meio de matrizes de peso linear. Por outro lado, os KANs colocam funções de ativação que podem ser aprendidas nas bordas (conexões) entre os neurônios, e não nos próprios neurônios. Na implementação original, essas funções são parametrizadas como B-splines, embora os autores mencionem que outros tipos de funções, como os polinômios de Chebyshev, também podem ser usados, dependendo do problema.

Os KANs superficiais e profundos dividem as funções complexas em uma série de funções mais simples e univariadas. A figura abaixo destaca essa diferença na arquitetura: Os MLPs usam ativações fixas dentro dos neurônios, enquanto os KANs implementam funções que podem ser aprendidas ao longo das bordas e as somam nos nós. Essa mudança arquitetônica permite que os KANs se adaptem dinamicamente aos dados, podendo alcançar maior precisão com menos parâmetros do que os MLPs. Além disso, após o treinamento, o modelo pode ser reduzido quando nem todas as bordas são usadas para aproximação.

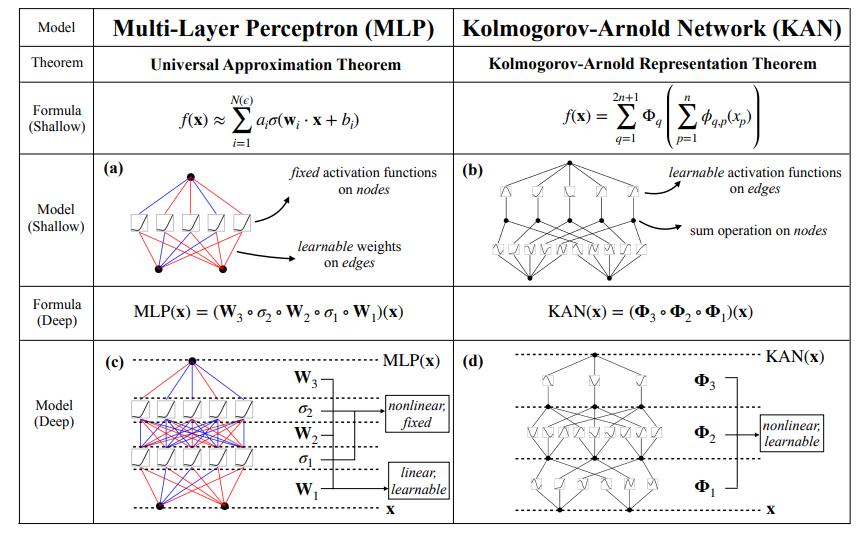
Fonte: Liu et al., 2024

Além disso, após o treinamento, os KANs nos permitem extrair as funções univariadas aprendidas, possibilitando a reconstrução da função multivariável resultante. Esse recurso é particularmente útil quando a interpretabilidade é crucial. Mais adiante, mostraremos esse processo na seção de exemplos.

pip install git+https://github.com/KindXiaoming/pykan.git

Uso

Depois de instalar o pykan, podemos começar a importar os módulos necessários e definir um KAN simples:

from kan import *
model = KAN(width=[2,5,1])

Aqui, especificamos as dimensões do modelo no parâmetro width. Nesse caso específico, estamos criando um modelo com 2 entradas, 1 saída e uma camada de 5 neurônios ocultos.Agora, vamos criar um conjunto de dados para o nosso experimento. Usarei um polinômio aleatório de duas variáveis que acabei de inventar na hora:

from kan.utils import create_dataset
f = lambda x: 3*x[:,[0]]**3+2*x[:,[0]]+4 + 2 * x[:,[0]] * x[:,[1]] ** 2 + 3 * x[:,[1]] ** 3
dataset = create_dataset(f, n_var=2)

Aqui, eu uso uma função lambda para definir um polinômio. A biblioteca parece usar a biblioteca numpy sob o capô - daí a sintaxe. Agora, podemos carregar o conjunto de dados em um modelo e visualizá-lo:

model(dataset['train_input']);
model.plot()

Aqui está a aparência do resultado:

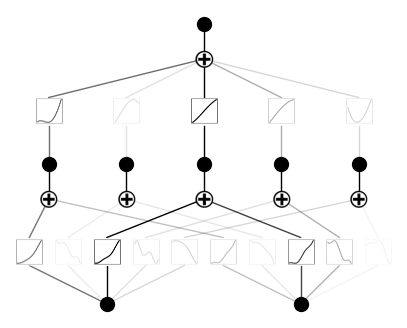
Treinamento

Para executar o treinamento, precisamos usar o método .fit():

model.fit(dataset, steps=1000);

Após o treinamento, este é o aspecto do nosso KAN:

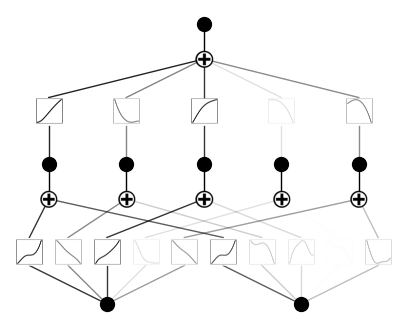
Agora, vamos podar e plotar o modelo novamente:

model = model.prune()
model.plot()

Aqui está a aparência do modelo agora. Como você pode ver, podamos uma função de ativação:

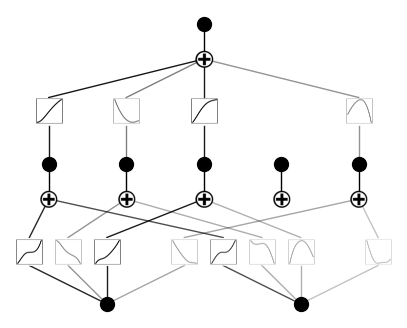
Isso faz sentido, pois nosso polinômio não usa cinco combinações diferentes de potências de variáveis de entrada.

Casos de uso de KANs

As redes de Kolmogorov-Arnold (KANs) têm se mostrado promissoras em vários campos devido à sua capacidade de modelar relações complexas e não lineares com menos parâmetros do que as redes neurais tradicionais. Aqui estão alguns casos de uso importantes:

• Modelagem científica e ajuste de dados: Os KANs são particularmente eficazes para problemas científicos que exigem modelagem precisa de funções complexas. Como os KANs aproximam funções multivariáveis por meio do aprendizado de funções univariadas mais simples, eles podem capturar com eficiência padrões complexos em dados científicos. Para tarefas como ajuste de curvas, os KANs geralmente superam os MLPs tradicionais devido à sua arquitetura flexível.
• Solução de equações diferenciais parciais (PDEs): Os KANs demonstraram grande potencial na solução de PDEs, que são comumente usados em física e engenharia para modelar processos como transferência de calor e dinâmica de fluidos. Sua capacidade de lidar com problemas não lineares e de alta dimensão os torna particularmente úteis nesse domínio, superando os MLPs em termos de precisão e interpretabilidade.
• Regressão simbólica: Os KANs são excelentes em regressão simbólica, em que o objetivo é descobrir expressões matemáticas que melhor descrevam um conjunto de dados. Sua capacidade de aprender estruturas de composição os torna uma ferramenta ideal para redescobrir leis físicas e matemáticas diretamente dos dados.

Vantagens e desvantagens das KANs

Vamos explorar algumas das maneiras pelas quais as KANs melhoram as limitações das redes neurais convencionais:

• Interpretabilidade: Diferentemente dos modelos tradicionais de aprendizagem profunda, os KANs oferecem uma estrutura mais interpretável. As funções aprendidas podem ser visualizadas e analisadas, oferecendo insights sobre o processo de tomada de decisão do modelo. Essa característica é particularmente valiosa em campos científicos, nos quais compreender o funcionamento do modelo é tão crucial quanto obter alta precisão.
• Flexibilidade: Os KANs não se limitam a um único tipo de função de ativação. Embora eles geralmente usem B-splines, outras funções de base, como polinômios de Chebyshev, podem ser empregadas com base na tarefa específica. Essa flexibilidade torna a arquitetura versátil e adaptável a uma variedade de aplicações.

Os KANs apresentam uma nova abordagem promissora para a aprendizagem profunda, mas, como qualquer tecnologia, eles têm seus próprios pontos fracos:

• Complexidade computacional: Um dos desafios dos KANs é sua intensidade computacional durante a fase de treinamento. Como os KANs usam funções de ativação que podem ser aprendidas nas bordas, a complexidade da avaliação dessas funções pode retardar significativamente o processo de treinamento em comparação com os MLPs tradicionais. Essa complexidade é ampliada ainda mais em tarefas que exigem arquiteturas KAN profundas ou funções de base altamente detalhadas.
• Necessidade de conhecimento especializado: A implementação e o ajuste dos KANs podem ser mais complexos do que trabalhar com MLPs tradicionais. A seleção das funções de base apropriadas (por exemplo, B-splines, polinômios de Chebyshev) e a configuração do modelo para uma tarefa específica exigem um entendimento matemático mais profundo e mais interação entre homem e modelo. Isso pode tornar as KANs menos acessíveis aos profissionais sem conhecimento especializado.

Interação humano-KAN

Um aspecto exclusivo das redes de Kolmogorov-Arnold (KANs) é sua capacidade de facilitar a interação significativa entre o modelo e a intuição humana. O artigo original descreve como os pesquisadores podem se envolver com o aprendizado do modelo de maneiras que não são possíveis com as redes neurais tradicionais.

Depois de treinar um KAN em um problema específico, os pesquisadores podem extrair as funções univariadas aprendidas que o modelo usa para aproximar a função multivariável complexa. Ao estudar essas funções aprendidas, os pesquisadores obtêm insights sobre as relações subjacentes nos dados.

Além disso, as percepções obtidas com essa interação permitem o refinamento iterativo. Os pesquisadores podem ajustar a arquitetura do KAN, modificar os tipos de funções básicas (por exemplo, mudar de B-splines para polinômios Chebyshev) ou ajustar o processo de treinamento com base nas funções extraídas. Essa abordagem humana no circuito permite um processo de modelagem personalizado, tornando os KANs adaptáveis a diferentes problemas científicos ou matemáticos.

Dessa forma, os KANs facilitam uma interação bidirecional: eles aprendem com os dados para formar funções complexas, e os humanos podem orientar e interpretar esse aprendizado para refinar o modelo ou até mesmo descobrir novos conhecimentos. Essa interação é o que faz com que os KANs se destaquem, transformando o aprendizado de máquina em um empreendimento mais colaborativo e exploratório.

Conclusão

De modo geral, as redes Kolmogorov-Arnold (KANs) representam um avanço empolgante e promissor na arquitetura de redes neurais. Seu design exclusivo oferece uma alternativa flexível e interpretável aos MLPs, com o potencial de superar os modelos tradicionais em várias tarefas.

À medida que a comunidade continua a explorar as KANs por meio de colaborações de código aberto e aplicativos diversos, essas redes e suas extensões podem evoluir para ferramentas avançadas e de última geração.