Réseaux Kolmogorov-Arnold (KAN) : Un guide avec mise en œuvre

Que sont les réseaux de Kolmogorov-Arnold (KAN) ?

Les réseaux de Kolmogorov-Arnold (KAN) reposent sur le théorème de représentation de Kolmogorov-Arnold, qui constitue leur fondement mathématique. Le théorème stipule que toute fonction continue à plusieurs variables peut être décomposée en une somme de fonctions plus simples à une seule variable.

Cependant, si le théorème garantit l'existence de ces fonctions univariées, il ne nous dit pas comment les trouver. C'est là que les KAN entrent en jeu.

Au lieu d'approximer directement une fonction complexe entière, comme le font la plupart des autres modèles, les KAN se concentrent sur l'apprentissage de ces fonctions univariées plus simples. Cette approche permet d'obtenir un modèle qui est non seulement flexible, mais aussi très facile à interpréter, en particulier lorsqu'il s'agit de traiter des relations non linéaires dans les données.

Réseaux de Kolmogorov-Arnold (KAN) vs. Perceptrons multicouches (MLP)

La principale différence entre les KAN et les perceptrons multicouches (MLP) traditionnels réside dans le mode d'apprentissage.

Dans les MLP, les neurones sont activés à l'aide de fonctions fixes telles que ReLU ou sigmoïde, et ces activations sont transmises à des matrices de poids linéaires. En revanche, les KAN placent les fonctions d'activation apprenables sur les bords (connexions) entre les neurones plutôt qu'au niveau des neurones eux-mêmes. Dans l'implémentation originale, ces fonctions sont paramétrées comme des B-splines, bien que les auteurs mentionnent que d'autres types de fonctions, telles que les polynômes de Chebyshev, peuvent également être utilisés en fonction du problème.

Les KAN, qu'elles soient profondes ou peu profondes, décomposent les fonctions complexes en une série de fonctions univariées plus simples. La figure ci-dessous illustre cette différence d'architecture : Les MLP utilisent des activations fixes dans les neurones, tandis que les KAN mettent en œuvre des fonctions apprenables le long des arêtes et les additionnent sur les nœuds. Ce changement d'architecture permet aux KAN de s'adapter dynamiquement aux données et d'atteindre potentiellement une plus grande précision avec moins de paramètres que les MLP. En outre, après l'apprentissage, le modèle peut être réduit si toutes les arêtes ne sont pas utilisées pour l'approximation.

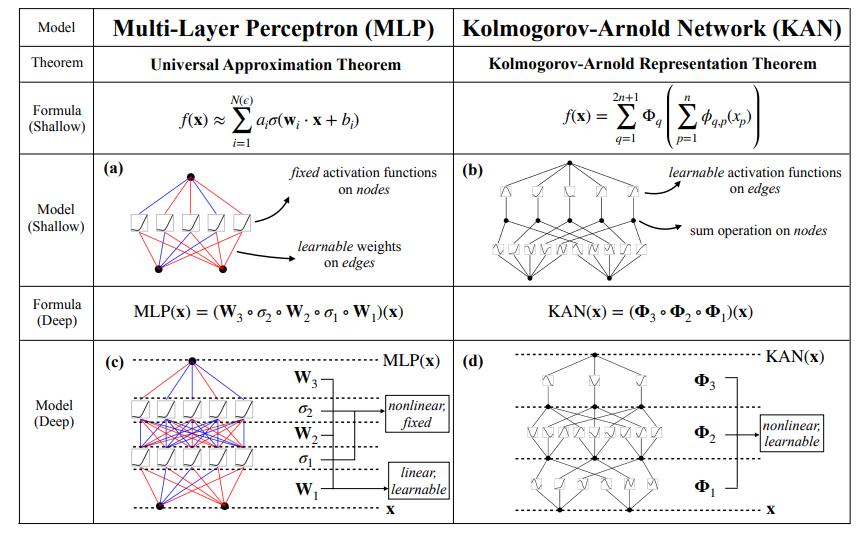
Source : Liu et al., 2024

En outre, après l'apprentissage, les KAN nous permettent d'extraire les fonctions univariées apprises, ce qui permet de reconstruire la fonction multivariable résultante. Cette caractéristique est particulièrement utile lorsque l'interprétabilité est cruciale. Nous présenterons ce processus dans la section des exemples plus loin.

pip install git+https://github.com/KindXiaoming/pykan.git

Utilisation

Après avoir installé pykan, nous pouvons commencer à importer les modules nécessaires et à définir un KAN simple :

from kan import *
model = KAN(width=[2,5,1])

Ici, nous spécifions les dimensions du modèle dans le paramètre width. Dans ce cas particulier, nous créons un modèle avec 2 entrées, 1 sortie et une couche de 5 neurones cachés.Créons maintenant un ensemble de données pour notre expérience. J'utiliserai un polynôme aléatoire à 2 variables que j'ai inventé à la volée :

from kan.utils import create_dataset
f = lambda x: 3*x[:,[0]]**3+2*x[:,[0]]+4 + 2 * x[:,[0]] * x[:,[1]] ** 2 + 3 * x[:,[1]] ** 3
dataset = create_dataset(f, n_var=2)

Ici, j'utilise une fonction lambda pour définir un polynôme. La bibliothèque semble utiliser la bibliothèque numpy sous le manteau, d'où la syntaxe. Nous pouvons maintenant charger l'ensemble de données dans un modèle et le visualiser :

model(dataset['train_input']);
model.plot()

Voici à quoi ressemble le résultat :

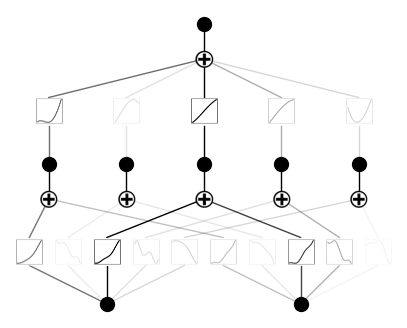
Formation

Afin d'exécuter la formation, nous devons utiliser la méthode .fit():

model.fit(dataset, steps=1000);

Après la formation, voici à quoi ressemble notre KAN :

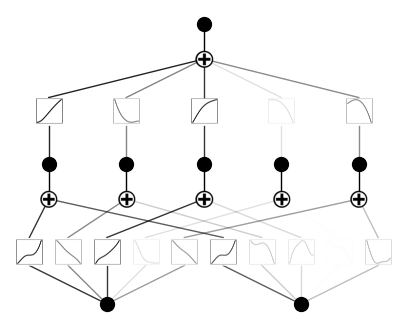
Maintenant, élaguons et traçons à nouveau le modèle :

model = model.prune()
model.plot()

Voici à quoi ressemble maintenant le modèle. Comme vous pouvez le constater, nous avons élagué une fonction d'activation :

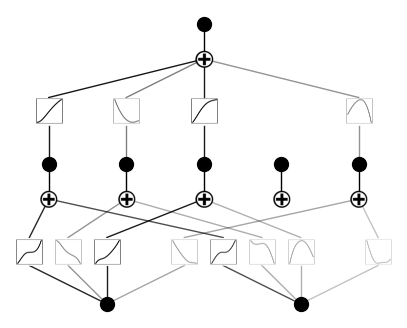
C'est logique, car notre polynôme n'utilise pas cinq combinaisons différentes de puissances de variables d'entrée.

Cas d'utilisation des KAN

Les réseaux Kolmogorov-Arnold (KAN) se sont révélés prometteurs dans divers domaines en raison de leur capacité à modéliser des relations complexes et non linéaires avec moins de paramètres que les réseaux neuronaux traditionnels. Voici quelques cas d'utilisation clés :

• Modélisation scientifique et ajustement des données: Les KAN sont particulièrement efficaces pour les problèmes scientifiques qui nécessitent une modélisation précise de fonctions complexes. Comme les KAN se rapprochent des fonctions multivariables en apprenant des fonctions univariées plus simples, ils peuvent capturer efficacement des modèles complexes dans les données scientifiques. Pour des tâches telles que l'ajustement de courbes, les KAN sont souvent plus performants que les MLP traditionnels en raison de la souplesse de leur architecture.
• Résolution d'équations aux dérivées partielles (EDP): Les KAN ont démontré un fort potentiel dans la résolution des EDP, qui sont couramment utilisées en physique et en ingénierie pour modéliser des processus tels que le transfert de chaleur et la dynamique des fluides. Leur capacité à traiter des problèmes non linéaires de haute dimension les rend particulièrement utiles dans ce domaine, surpassant les MLP en termes de précision et d'interprétabilité.
• Régression symbolique: Les KAN excellent dans la régression symbolique, où l'objectif est de découvrir les expressions mathématiques qui décrivent le mieux un ensemble de données. Leur capacité à apprendre des structures de composition en fait un outil idéal pour redécouvrir des lois physiques et mathématiques directement à partir de données.

Avantages et inconvénients des KAN

Examinons quelques-unes des améliorations apportées par les KAN aux limites des réseaux neuronaux conventionnels :

• Interprétabilité: Contrairement aux modèles d'apprentissage profond traditionnels, les KAN offrent une structure plus facile à interpréter. Les fonctions pouvant être apprises peuvent être visualisées et analysées, ce qui permet de mieux comprendre le processus de prise de décision du modèle. Cette caractéristique est particulièrement précieuse dans les domaines scientifiques, où la compréhension du fonctionnement du modèle est tout aussi cruciale que l'obtention d'une grande précision.
• Flexibilité: Les KAN ne sont pas limités à un seul type de fonction d'activation. Bien qu'ils utilisent souvent des B-splines, d'autres fonctions de base, telles que les polynômes de Chebyshev, peuvent être employées en fonction de la tâche spécifique. Cette flexibilité rend l'architecture polyvalente et adaptable à toute une série d'applications.

Les KAN constituent une nouvelle approche prometteuse de l'apprentissage en profondeur, mais comme toute technologie, ils présentent leurs propres faiblesses :

• Complexité calculatoire: L'un des défis posés par les KAN est leur intensité de calcul pendant la phase de formation. Étant donné que les KAN utilisent des fonctions d'activation apprenables sur les arêtes, la complexité de l'évaluation de ces fonctions peut ralentir considérablement le processus d'apprentissage par rapport aux MLP traditionnels. Cette complexité est encore amplifiée dans les tâches qui nécessitent des architectures KAN profondes ou des fonctions de base très détaillées.
• Besoin d'expertise: La mise en œuvre et le réglage des KAN peuvent s'avérer plus complexes que l'utilisation des MLP traditionnels. La sélection des fonctions de base appropriées (par exemple, B-splines, polynômes de Chebyshev) et la configuration du modèle pour une tâche spécifique nécessitent une compréhension mathématique plus approfondie et une interaction plus importante entre l'homme et le modèle. Cela peut rendre les KAN moins accessibles aux praticiens qui n'ont pas de connaissances spécialisées.

Interaction entre l'homme et le réseau KAN

Un aspect unique des réseaux de Kolmogorov-Arnold (KAN) est leur capacité à faciliter une interaction significative entre le modèle et l'intuition humaine. L'article original décrit comment les chercheurs peuvent s'impliquer dans l'apprentissage du modèle d'une manière qui n'est pas possible avec les réseaux neuronaux traditionnels.

Après avoir formé un KAN à un problème spécifique, les chercheurs peuvent extraire les fonctions univariées apprises que le modèle utilise pour approximer la fonction multivariable complexe. L'étude de ces fonctions apprises permet aux chercheurs de mieux comprendre les relations sous-jacentes dans les données.

En outre, les connaissances acquises grâce à cette interaction permettent de procéder à des améliorations itératives. Les chercheurs peuvent adapter l'architecture du KAN, modifier les types de fonctions de base (par exemple, passer des B-splines aux polynômes de Chebyshev) ou ajuster le processus d'apprentissage sur la base des fonctions extraites. Cette approche humaine dans la boucle permet un processus de modélisation sur mesure, rendant les KAN adaptables à différents problèmes scientifiques ou mathématiques.

De cette manière, les KAN facilitent une interaction à double sens : ils apprennent à partir des données pour former des fonctions complexes, et les humains peuvent guider et interpréter cet apprentissage pour affiner le modèle ou même découvrir de nouvelles connaissances. C'est cette interaction qui permet aux KAN de se démarquer, en transformant l'apprentissage automatique en une entreprise plus collaborative et exploratoire.

Conclusion

Dans l'ensemble, les réseaux de Kolmogorov-Arnold (KAN) représentent une avancée passionnante et prometteuse dans l'architecture des réseaux neuronaux. Leur conception unique offre une alternative flexible et interprétable aux MLP, avec le potentiel de surpasser les modèles traditionnels dans diverses tâches.

Alors que la communauté continue d'explorer les KAN par le biais de collaborations à code source ouvert et d'applications diverses, ces réseaux et leurs extensions pourraient devenir de puissants outils de pointe.