Curso
En mi viaje de una década por las finanzas cuantitativas, me he encontrado con numerosas distribuciones estadísticas, pero pocas han demostrado tener un nombre tan intrigante y a la vez tan valioso en la práctica como la distribución binomial negativa. Mientras analizaba patrones de negociación y modelos de riesgo, descubrí que esta distribución, a pesar de su nombre aparentemente pesimista, ofrece una visión de los procesos de recuento que muchos modelos más sencillos no consiguen captar.
La distribución binomial negativa proporciona un marco sofisticado para modelizar tales escenarios, ofreciendo mayor flexibilidad que sus homólogas más sencillas, como la distribución de Poisson. Sirve como extensión natural de la distribución binomial, adaptándose a situaciones en las que necesitamos modelizar el número de ensayos hasta que se produzca un determinado número de sucesos, en lugar del número de sucesos en un número fijo de ensayos.
En esta completa guía, exploraremos los fundamentos matemáticos de la distribución binomial negativa, sus aplicaciones prácticas y su implementación en Python y R. Partiendo de sus propiedades básicas y llegando hasta las aplicaciones avanzadas, construiremos un conocimiento profundo de esta potente herramienta estadística.
¿Qué es la Distribución Binomial Negativa?
La distribución binomial negativa se originó en el siglo XVIII mediante el estudio de la probabilidad en los juegos de azar. Esta distribución de probabilidad discreta modela el número de fallos en una secuencia de ensayos Bernoulli independientes antes de alcanzar un número predeterminado de éxitos. Cada ensayo debe ser independiente y tener la misma probabilidad de éxito.
Para comprender intuitivamente esta distribución, considera un experimento sencillo: entrevistar a candidatos hasta encontrar tres cualificados para un puesto. La distribución modelaría el número de entrevistas fallidas (fracasos) necesarias antes de encontrar a esos tres candidatos cualificados (éxitos). Esto difiere fundamentalmente de la distribución binomial, que en cambio modela el número de aciertos en un número fijo de ensayos, como el número de candidatos cualificados encontrados en exactamente 20 entrevistas.
Como ves, aunque el nombre "binomio negativo" pueda hacer que te sorprendas, no implica nada negativo en el sentido convencional. El aspecto "negativo" proviene de su derivación histórica con exponentes negativos.
Dónde se utiliza la Distribución Binomial Negativa
La distribución binomial negativa se utiliza de muchas formas distintas. Se utiliza en finanzas, que es donde más lo sitúo, donde modela escenarios como el número de días de negociación hasta alcanzar un nivel de beneficios objetivo, o el número de solicitudes de crédito revisadas antes de encontrar un determinado número de prestatarios cualificados.
De forma más general, la distribución binomial negativa también ha demostrado ser valiosa para modelar datos de recuento cuando la varianza supera a la media, fenómeno conocido como sobredispersión. Aunque la distribución de Poisson supone que la media es igual a la varianza, los datos de recuento del mundo real suelen mostrar una mayor variabilidad. Por ejemplo, en epidemiología, el número de casos de enfermedad suele variar más de lo que predeciría un modelo de Poisson, lo que hace que la distribución binomial negativa sea más apropiada para modelizar la propagación de la enfermedad.
Los genetistas se basan en esta distribución cuando analizan los datos de secuenciación. En los experimentos de secuenciación del ARN, los genes muestran distintos niveles de expresión con una gran variabilidad. La binomial negativa modela el número de lecturas de secuencias asignadas a cada gen, teniendo en cuenta tanto la variación técnica como la biológica. Esto ayuda a identificar los genes expresados diferencialmente con más precisión que los métodos que suponen una varianza constante.
En los estudios ecológicos, los investigadores lo utilizan para modelizar la abundancia de especies. Considera el estudio de las poblaciones de aves: algunas zonas pueden tener pocas aves mientras que otras tienen grandes grupos, lo que crea una varianza mayor de la esperada. La binomial negativa modela eficazmente estas distribuciones agrupadas, ayudando a los ecólogos a comprender la dinámica de las poblaciones y a planificar los esfuerzos de conservación.
Características de la distribución binomial negativa
La distribución binomial negativa se caracteriza por dos parámetros clave que determinan su forma y comportamiento. Comprender estos parámetros y la representación matemática nos ayuda a entender cómo esta distribución modela los fenómenos del mundo real. Exploremos sistemáticamente estas características.
Representación matemática y parámetros
La distribución binomial negativa tiene dos parámetros fundamentales:
- r - El número objetivo de aciertos (un número entero positivo)
- p - La probabilidad de éxito en cada ensayo (entre 0 y 1)
Estos parámetros determinan el comportamiento de la distribución. Considera la posibilidad de hacer un seguimiento del número de llamadas de ventas necesarias para conseguir cinco nuevos clientes (r = 5) cuando cada llamada tiene un 20% de probabilidades de éxito (p = 0,2). El valor de r determina nuestro punto de parada, mientras que p influye en cuánto tiempo podemos esperar seguir haciendo llamadas.
Cuando aumentamos r manteniendo p constante, la distribución se desplaza hacia la derecha y se vuelve más dispersa, lo que refleja que necesitamos más ensayos para conseguir más éxitos. Por el contrario, cuando aumentamos p manteniendo r constante, la distribución se desplaza hacia la izquierda y se concentra más, lo que indica que normalmente se necesitan menos ensayos cuando el éxito es más probable.
Función de masa de probabilidad (FMP) y función de distribución acumulativa (FDA)
La función de masa de probabilidad nos da la probabilidad de necesitar exactamente k fracasos antes de conseguir r éxitos. Para la distribución binomial negativa, la PMF es:
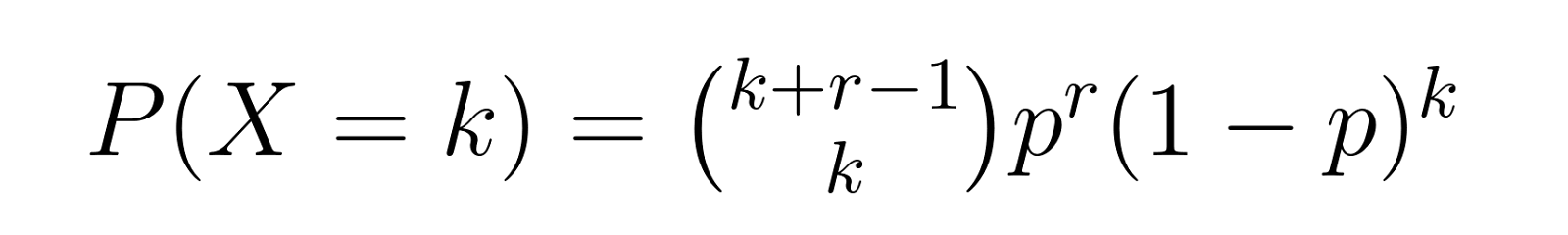
Dónde:
- X representa el número de fracasos antes de conseguir r éxitos
- (k+r-1 elige k) es el coeficiente binomial, que representa el número de formas de disponer k fallos y r-1 aciertos
- p es la probabilidad de éxito
- r es el número deseado de aciertos
- K es el número de fallos
Ejemplo: En control de calidad, si necesitamos 3 unidades defectuosas (r = 3) y cada unidad tiene un 10% de probabilidades de ser defectuosa (p = 0,1), podemos calcular probabilidades específicas. Por ejemplo, la probabilidad de obtener exactamente 5 unidades no defectuosas (k = 5) antes de encontrar la tercera defectuosa es:
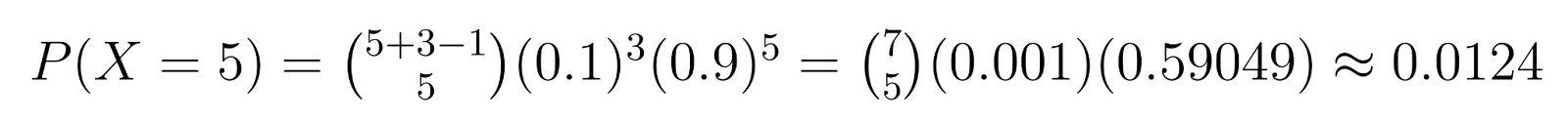
Este cálculo muestra aproximadamente un 1,24% de probabilidades de necesitar exactamente 5 unidades no defectuosas antes de encontrar la tercera defectuosa.
La función de distribución acumulativa (FDC) se basa en la FMP, y nos da la probabilidad de necesitar k o menos fallos antes de alcanzar nuestro número objetivo de éxitos:
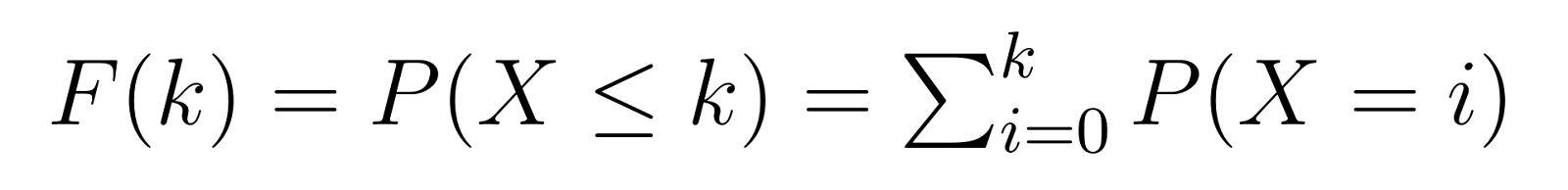
Esto significa que F(k) nos da la probabilidad de necesitar como máximo k unidades no defectuosas antes de encontrar la tercera defectuosa. Por ejemplo, F(5) nos daría la probabilidad de necesitar 5 o menos unidades no defectuosas.
Media y varianza
La media (valor esperado) y la varianza de la distribución binomial negativa tienen fórmulas elegantes que revelan propiedades importantes sobre la media (μ) y la varianza (σ²).
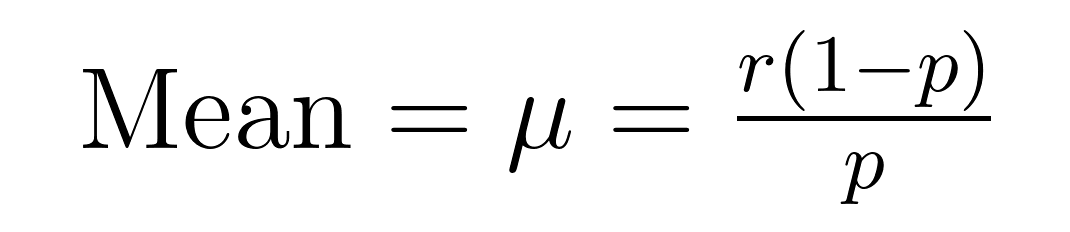
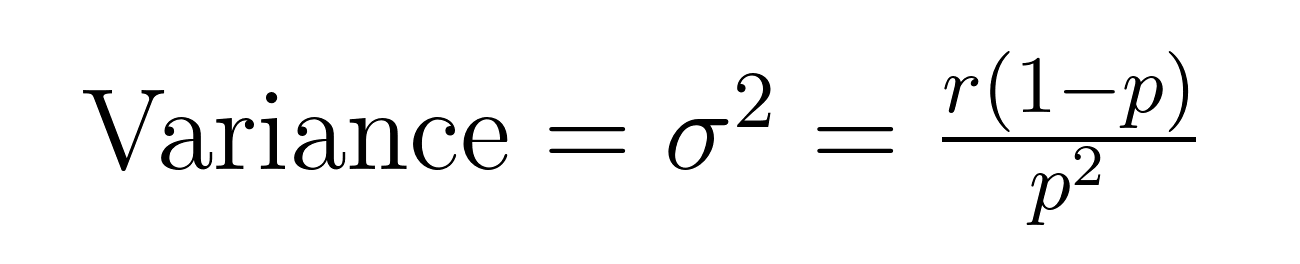
Estas fórmulas demuestran por qué esta distribución destaca en el modelado de datos sobredispersos. Observa que la varianza siempre es mayor que la media por un factor de 1/p. Esta propiedad incorporada la hace naturalmente adecuada para conjuntos de datos en los que la variabilidad supera a la media.
Por ejemplo, si estamos modelando llamadas de atención al cliente en las que esperamos resolver 5 casos (r = 5) con una tasa de éxito del 20% por intento (p = 0,2), el número esperado de intentos fallidos sería:
- Media = 5(1-0,2)/0,2 = 20 fallos
- Varianza = 5(1-0,2)/0,2² = 100
Esta mayor varianza tiene en cuenta la realidad de que algunos casos pueden resolverse rápidamente mientras que otros requieren muchos más intentos, un patrón que se observa a menudo en escenarios del mundo real.
Comprender estas características nos ayuda a reconocer cuándo aplicar la distribución binomial negativa y cómo interpretar sus resultados con eficacia. Estos fundamentos matemáticos sientan las bases para las aplicaciones prácticas y la implementación, que exploraremos en secciones posteriores.
Implementación en Python y R
Validemos nuestro ejemplo anterior: calculando la probabilidad de obtener exactamente 5 unidades no defectuosas antes de encontrar la tercera defectuosa (r=3, p=0,1).
Implementación de Python
import scipy.stats as stats
import math
def calculate_nb_pmf(k, r, p):
# Calculate binomial coefficient (k+r-1 choose k)
binom_coef = math.comb(k + r - 1, k)
# Calculate p^r * (1-p)^k
prob = (p ** r) * ((1 - p) ** k)
return binom_coef * prob
# Our example parameters
k = 5 # failures (non-defective units)
r = 3 # successes (defective units)
p = 0.1 # probability of success (defective)
# Calculate using our function
prob_manual = calculate_nb_pmf(k, r, p)
print(f"Manual calculation: {prob_manual:.4f}")
# Verify using scipy
prob_scipy = stats.nbinom.pmf(k, r, p)
print(f"SciPy calculation: {prob_scipy:.4f}")El fragmento de código anterior debería mostrar lo siguiente:
Manual calculation: 0.0124
SciPy calculation: 0.0124Ejecución R
# Calculate probability mass function
k <- 5 # failures (non-defective units)
r <- 3 # successes (defective units)
p <- 0.1 # probability of success (defective)
# Using dnbinom
prob_r <- dnbinom(k, size = r, prob = p)
print(sprintf("R calculation: %.4f", prob_r))
# Manual calculation for verification
manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k
print(sprintf("Manual calculation: %.4f", manual_calc))El fragmento de código anterior debería arrojar los mismos números que nuestro ejemplo de Python:
R calculation: 0.0124
Manual Calculation: 0.0124Ambas implementaciones confirman nuestra anterior probabilidad calculada de aproximadamente 0,0124 o 1,24%.
Relación con otras distribuciones
Comprender cómo se relaciona la distribución binomial negativa con otras distribuciones de probabilidad ayuda a aclarar cuándo utilizar cada una de ellas. La distribución binomial negativa tiene conexiones únicas con varias distribuciones importantes en estadística.
Distribución binomial negativa vs. distribución binomial
La distribución binomial sirve como punto de partida fundacional. Mientras que la distribución binomial cuenta los aciertos en un número fijo de ensayos, la binomial negativa invierte este concepto contando los ensayos necesarios para un número fijo de aciertos. Estas distribuciones son complementarias: si necesitas exactamente 3 aciertos y quieres saber la probabilidad de conseguirlo en exactamente 8 ensayos, utiliza la distribución binomial. Si quieres saber la probabilidad de necesitar exactamente 8 ensayos para obtener 3 aciertos, utiliza la binomial negativa.
Distribución binomial negativa vs. Distribución de Poisson
La distribución de Poisson se compara a menudo con la binomial negativa cuando se modelan datos de recuento. Ambos manejan eventos discretos, pero difieren en sus supuestos de varianza. La característica que define a la distribución de Poisson es que su media es igual a su varianza. Sin embargo, los datos de recuento del mundo real presentan con frecuencia una dispersión excesiva, en la que la varianza supera a la media. La distribución binomial negativa acomoda de forma natural esta variabilidad extra, lo que la hace más adecuada para fenómenos como:
- Patrones de brotes de enfermedades en los que algunos casos conducen a muchas más infecciones
- Datos de reclamaciones de clientes en los que algunos problemas desencadenan múltiples reclamaciones relacionadas
- Picos de tráfico en el sitio web cuando determinados acontecimientos provocan niveles de actividad elevados
Distribución binomial negativa vs. distribución geométrica
La distribución geométrica surge como un caso especial de la binomial negativa cuando fijamos r=1, lo que significa que esperamos un solo éxito. Esto lo hace perfecto para modelar escenarios como:
- Número de intentos hasta el primer éxito
- Tiempo hasta el primer fallo en las pruebas de fiabilidad
- Número de ensayos hasta el primer avance en la investigación
Distribución binomial negativa como mezcla Gamma-Poisson
Por último, la binomial negativa puede derivarse como una mezcla Gamma-Poisson, lo que proporciona un fundamento teórico para su capacidad de manejar la sobredispersión. Esta relación ayuda a explicar por qué la distribución binomial negativa funciona bien en modelos jerárquicos en los que las tasas individuales de ocurrencia varían según una distribución gamma.
Ventajas y limitaciones
La distribución binomial negativa ofrece distintas ventajas que la hacen valiosa para modelar fenómenos del mundo real, aunque también tiene importantes limitaciones que los científicos de datos deben tener en cuenta.
| Ventajas | Limitaciones |
|---|---|
| Maneja con flexibilidad los datos sobredispersos cuando la varianza supera a la media | Requiere independencia entre juicios/eventos |
| Los parámetros tienen interpretaciones claras para su uso práctico | La estimación de parámetros se vuelve poco fiable con muestras pequeñas |
| Acomoda tanto recuentos como proporciones | Computacionalmente más intensiva que las distribuciones más simples |
| Modela naturalmente la agrupación en datos de recuento | Puede sobreajustarse cuando los datos no están realmente sobredispersos |
| Funciona bien con series temporales y datos longitudinales | Supone una probabilidad constante de éxito en todos los ensayos |
Regresión Binomial Negativa
La regresión binomial negativa amplía la regresión tradicional a los datos de recuento, sobre todo cuando los datos muestran sobredispersión. Mientras que la regresión de Poisson supone que la media es igual a la varianza, la regresión binomial negativa relaja esta restricción, lo que la hace más adecuada para las aplicaciones del mundo real.
Considera un escenario de centro de llamadas: Queremos predecir el número de llamadas de atención al cliente por hora. Nuestros predictores podrían incluir:
- Hora del día
- Día de la semana
- Estado de vacaciones
- Actividad de la campaña de marketing
- Condiciones meteorológicas
La regresión de Poisson estándar podría subestimar la variación del volumen de llamadas, sobre todo en horas punta o eventos especiales. La regresión binomial negativa tiene en cuenta esta variabilidad adicional, proporcionando predicciones e intervalos de confianza más realistas.
Conclusión
Gracias a su capacidad para modelizar datos de recuento complejos y manejar la sobredispersión, la distribución binomial negativa sigue siendo una herramienta esencial para comprender y predecir los fenómenos del mundo real. Como has visto, destaca en el modelado de datos sobredispersos, proporciona flexibilidad para modelar un gran número de escenarios diferentes, e incluso se extiende de forma natural al análisis de regresión.
Si te interesa profundizar en el conocimiento de las distribuciones de probabilidad y sus aplicaciones, nuestros cursos de Probabilidad y Estadística ofrecen una cobertura completa de estos temas. Nuestros cursos incluyen ejercicios prácticos con conjuntos de datos del mundo real, que te ayudarán a dominar tanto los conceptos teóricos como las implementaciones prácticas en Python y R. Considera también nuestro itinerario profesional de Científico de Aprendizaje Automático en Python. Te prometo que aprenderás mucho.
Como profesional experto en Ciencia de Datos, Aprendizaje Automático e IA Generativa, Vinod se dedica a compartir conocimientos y a capacitar a los aspirantes a científicos de datos para que tengan éxito en este dinámico campo.
Preguntas y respuestas sobre la distribución binomial negativa
¿Qué es la distribución binomial negativa?
La distribución binomial negativa modela el número de ensayos necesarios para conseguir un número determinado de aciertos en una secuencia de ensayos Bernoulli independientes e idénticamente distribuidos.
¿En qué se diferencia la distribución binomial negativa de la distribución de Poisson?
La distribución binomial negativa tiene en cuenta la sobredispersión en los datos de recuento, a diferencia de la distribución de Poisson, que asume igual media y varianza.
¿Cuáles son los parámetros de la distribución binomial negativa?
Los parámetros clave son el número de aciertos (r) y la probabilidad de acierto (p) en cada ensayo.
¿Cuándo debo utilizar la distribución binomial negativa?
Utilízalo cuando modelices datos de recuento con sobredispersión, en los que la varianza supera a la media.
¿Cuál es la función de masa de probabilidad de la distribución binomial negativa?
La PMF da la probabilidad de conseguir un número determinado de aciertos en un número dado de ensayos.
¿Cómo calculo probabilidades utilizando la distribución binomial negativa?
Utiliza la fórmula PMF o un programa estadístico para calcular las probabilidades en función de los parámetros de la distribución.
¿Qué es la dispersión excesiva en los datos de recuento?
La sobredispersión se produce cuando la varianza de los datos de recuento supera la media, a menudo abordada por la distribución binomial negativa.


