Curso
Em minha jornada de uma década em finanças quantitativas, encontrei várias distribuições estatísticas, mas poucas tiveram um nome tão intrigante e valioso na prática quanto a distribuição binomial negativa. Ao analisar padrões de negociação e modelos de risco, descobri que essa distribuição, apesar de seu nome aparentemente pessimista, oferece insights sobre processos de contagem que muitos modelos mais simples não conseguem captar.
A distribuição binomial negativa fornece uma estrutura sofisticada para modelar esses cenários, oferecendo maior flexibilidade do que suas contrapartes mais simples, como a distribuição de Poisson. Ela serve como uma extensão natural da distribuição binomial, adaptando-se a situações em que precisamos modelar o número de tentativas até que um determinado número de eventos ocorra, em vez do número de eventos em um número fixo de tentativas.
Neste guia abrangente, exploraremos os fundamentos matemáticos, as aplicações práticas e a implementação da distribuição binomial negativa em Python e R. Começando por suas propriedades básicas e passando para as aplicações avançadas, desenvolveremos uma compreensão completa dessa poderosa ferramenta estatística.
O que é distribuição binomial negativa?
A distribuição binomial negativa teve origem no século 18 com o estudo da probabilidade em jogos de azar. Essa distribuição de probabilidade discreta modela o número de falhas em uma sequência de tentativas independentes de Bernoulli antes de atingir um número predeterminado de sucessos. Cada tentativa deve ser independente e ter a mesma probabilidade de sucesso.
Para entender essa distribuição intuitivamente, considere um experimento simples: entrevistar candidatos até encontrar três qualificados para um cargo. A distribuição modelaria o número de entrevistas malsucedidas (falhas) necessárias antes de encontrar esses três candidatos qualificados (sucessos). Isso difere fundamentalmente da distribuição binomial, que, em vez disso, modela o número de sucessos em um número fixo de tentativas, como o número de candidatos qualificados encontrados em exatamente 20 entrevistas.
Assim, você pode ver que, embora o nome "binômio negativo" possa causar estranheza, ele não implica nada negativo no sentido convencional. O aspecto "negativo" decorre de sua derivação histórica envolvendo expoentes negativos.
Onde a distribuição binomial negativa é usada
A distribuição binomial negativa é usada de muitas maneiras diferentes. Ele é usado em finanças, que é onde eu mais o coloco, onde modela cenários como o número de dias de negociação até atingir um nível de lucro desejado ou o número de solicitações de crédito analisadas antes de encontrar um determinado número de mutuários qualificados.
De modo mais geral, a distribuição binomial negativa também se mostrou valiosa para modelar dados de contagem quando a variação excede a média, um fenômeno conhecido como dispersão excessiva. Embora a distribuição de Poisson pressuponha que a média seja igual à variância, os dados de contagem do mundo real geralmente apresentam maior variabilidade. Por exemplo, na epidemiologia, o número de casos de doenças geralmente varia mais do que um modelo de Poisson poderia prever, tornando a distribuição binomial negativa mais apropriada para modelar a propagação de doenças.
Os geneticistas se baseiam nessa distribuição ao analisar dados de sequenciamento. Em experimentos de sequenciamento de RNA, os genes apresentam níveis de expressão variáveis com alta variabilidade. O binômio negativo modela o número de leituras de sequência mapeadas para cada gene, levando em conta a variação técnica e biológica. Isso ajuda a identificar genes expressos diferencialmente com mais precisão do que os métodos que pressupõem uma variação constante.
Em estudos ecológicos, os pesquisadores o utilizam para modelar a abundância de espécies. Considere o estudo de populações de aves: algumas áreas podem ter poucas aves, enquanto outras têm grandes grupos, criando uma variação maior do que a esperada. O binômio negativo modela com eficácia essas distribuições agrupadas, ajudando os ecologistas a entender a dinâmica da população e a planejar os esforços de conservação.
Características da distribuição binomial negativa
A distribuição binomial negativa é caracterizada por dois parâmetros-chave que determinam sua forma e comportamento. A compreensão desses parâmetros e da representação matemática nos ajuda a entender como essa distribuição modela os fenômenos do mundo real. Vamos explorar essas características de forma sistemática.
Representação matemática e parâmetros
A distribuição binomial negativa tem dois parâmetros fundamentais:
- r - O número alvo de sucessos (um número inteiro positivo)
- p - A probabilidade de sucesso em cada tentativa (entre 0 e 1)
Esses parâmetros definem como a distribuição se comporta. Considere acompanhar o número de chamadas de vendas necessárias para garantir cinco novos clientes (r = 5) quando cada chamada tem 20% de chance de sucesso (p = 0,2). O valor de r determina nosso ponto de parada, enquanto p influencia o tempo que podemos esperar para continuar fazendo chamadas.
Quando aumentamos r mantendo p constante, a distribuição se desloca para a direita e se torna mais espalhada, refletindo que precisamos de mais tentativas para obter mais sucessos. Por outro lado, quando aumentamos p e mantemos r constante, a distribuição se desloca para a esquerda e se torna mais concentrada, indicando que normalmente são necessárias menos tentativas quando o sucesso é mais provável.
Função de massa de probabilidade (PMF) e função de distribuição cumulativa (CDF)
A função de massa de probabilidade nos dá a probabilidade de exigir exatamente k falhas antes de obter r sucessos. Para a distribuição binomial negativa, o PMF é:
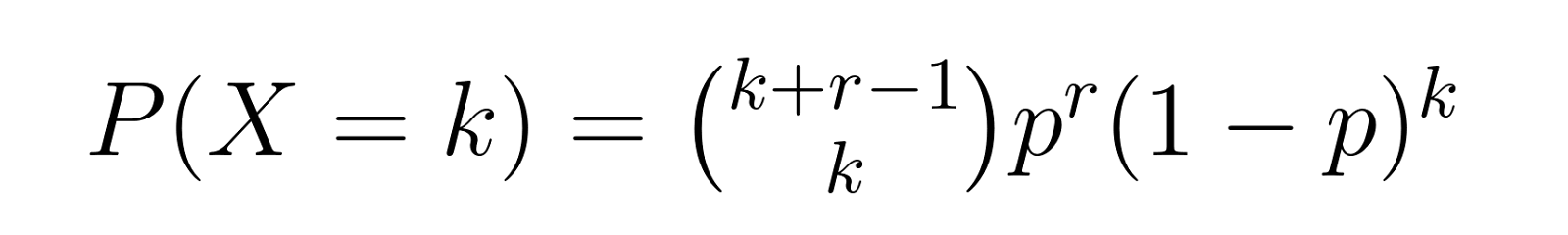
Onde:
- X representa o número de falhas antes de obter r sucessos
- (k+r-1 escolha k) é o coeficiente binomial, representando o número de maneiras de organizar k falhas e r-1 sucessos
- p é a probabilidade de sucesso
- r é o número desejado de sucessos
- K é o número de falhas
Exemplo: No controle de qualidade, se precisarmos de 3 unidades defeituosas (r = 3) e cada unidade tiver 10% de chance de ser defeituosa (p = 0,1), poderemos calcular probabilidades específicas. Por exemplo, a probabilidade de obter exatamente 5 unidades não defeituosas (k = 5) antes de encontrar a terceira defeituosa é:
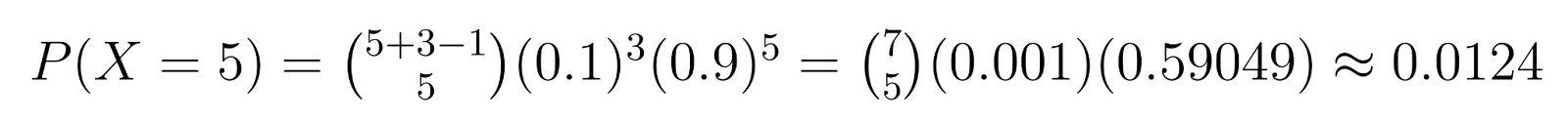
Esse cálculo mostra uma chance de 1,24% de precisar de exatamente 5 unidades não defeituosas antes de encontrar a terceira defeituosa.
A função de distribuição cumulativa (CDF) baseia-se na PMF, fornecendo a probabilidade de você precisar de k ou menos falhas antes de atingir a meta de número de sucessos:
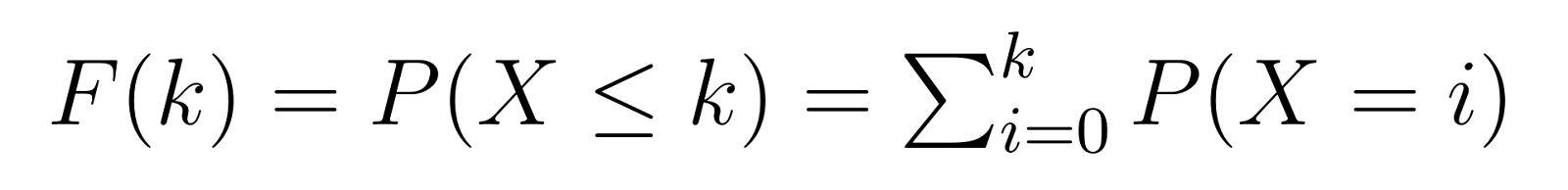
Isso significa que F(k) nos dá a probabilidade de precisarmos de, no máximo, k unidades não defeituosas antes de encontrarmos a terceira defeituosa. Por exemplo, F(5) nos daria a probabilidade de precisarmos de 5 ou menos unidades não defeituosas.
Média e variância
A média (valor esperado) e a variação da distribuição binomial negativa têm fórmulas elegantes que revelam propriedades importantes sobre a média (μ) e a variação (σ²).
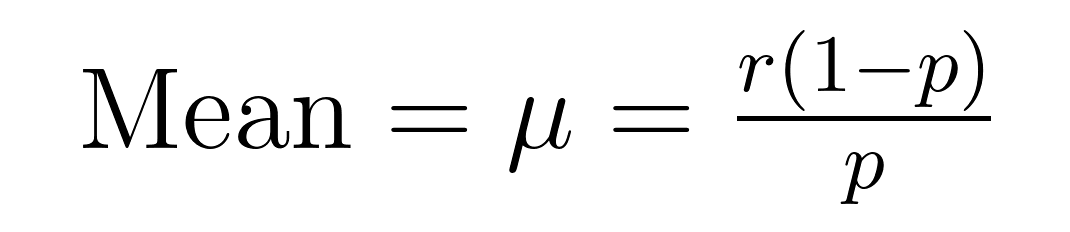
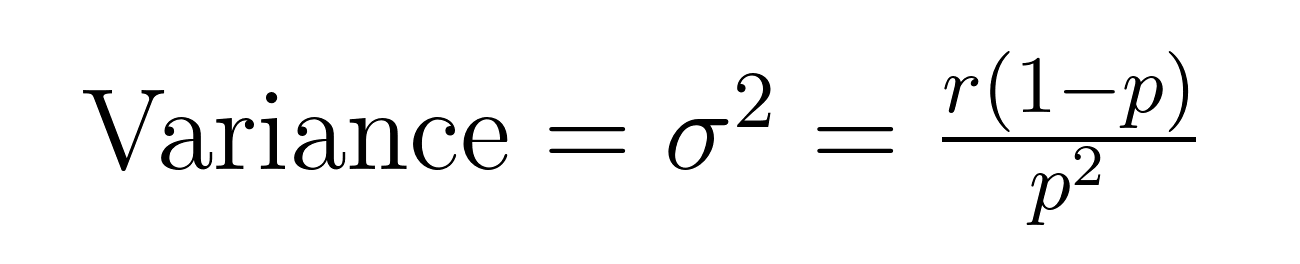
Essas fórmulas demonstram por que essa distribuição é excelente na modelagem de dados superdispersos. Observe que a variação é sempre maior do que a média por um fator de 1/p. Essa propriedade integrada o torna naturalmente adequado para conjuntos de dados em que a variabilidade excede a média.
Por exemplo, se estivermos modelando chamadas de atendimento ao cliente em que esperamos resolver 5 casos (r = 5) com uma taxa de sucesso de 20% por tentativa (p = 0,2), o número esperado de tentativas fracassadas seria:
- Média = 5(1-0,2)/0,2 = 20 falhas
- Variância = 5(1-0,2)/0,2² = 100
Essa variação maior leva em conta o fato de que alguns casos podem ser resolvidos rapidamente, enquanto outros exigem muito mais tentativas, um padrão frequentemente observado em cenários do mundo real.
A compreensão dessas características nos ajuda a reconhecer quando aplicar a distribuição binomial negativa e como interpretar seus resultados de forma eficaz. Esses fundamentos matemáticos preparam o terreno para aplicações práticas e implementação, que exploraremos nas seções seguintes.
Implementação em Python e R
Vamos validar nosso exemplo anterior: calcular a probabilidade de obter exatamente 5 unidades não defeituosas antes de encontrar a terceira defeituosa (r=3, p=0,1).
Implementação do Python
import scipy.stats as stats
import math
def calculate_nb_pmf(k, r, p):
# Calculate binomial coefficient (k+r-1 choose k)
binom_coef = math.comb(k + r - 1, k)
# Calculate p^r * (1-p)^k
prob = (p ** r) * ((1 - p) ** k)
return binom_coef * prob
# Our example parameters
k = 5 # failures (non-defective units)
r = 3 # successes (defective units)
p = 0.1 # probability of success (defective)
# Calculate using our function
prob_manual = calculate_nb_pmf(k, r, p)
print(f"Manual calculation: {prob_manual:.4f}")
# Verify using scipy
prob_scipy = stats.nbinom.pmf(k, r, p)
print(f"SciPy calculation: {prob_scipy:.4f}")O trecho de código acima deve produzir o seguinte:
Manual calculation: 0.0124
SciPy calculation: 0.0124Implementação da R
# Calculate probability mass function
k <- 5 # failures (non-defective units)
r <- 3 # successes (defective units)
p <- 0.1 # probability of success (defective)
# Using dnbinom
prob_r <- dnbinom(k, size = r, prob = p)
print(sprintf("R calculation: %.4f", prob_r))
# Manual calculation for verification
manual_calc <- choose(k + r - 1, k) * p^r * (1-p)^k
print(sprintf("Manual calculation: %.4f", manual_calc))O trecho de código acima deve gerar os mesmos números do nosso exemplo em Python:
R calculation: 0.0124
Manual Calculation: 0.0124Ambas as implementações confirmam nossa probabilidade calculada anteriormente de aproximadamente 0,0124 ou 1,24%.
Relação com outras distribuições
Entender como a distribuição binomial negativa se relaciona com outras distribuições de probabilidade ajuda a esclarecer quando você deve usar cada uma delas. A distribuição binomial negativa tem conexões exclusivas com várias distribuições importantes em estatística.
Distribuição binomial negativa vs. distribuição binomial
A distribuição binomial serve como um ponto de partida fundamental. Enquanto a distribuição binomial conta os sucessos em um número fixo de tentativas, a binomial negativa inverte esse conceito ao contar as tentativas necessárias para um número fixo de sucessos. Essas distribuições são complementares - se você precisar de exatamente 3 sucessos e quiser saber a probabilidade de conseguir isso em exatamente 8 tentativas, use a distribuição binomial. Se você quiser saber a probabilidade de precisar de exatamente 8 tentativas para obter 3 sucessos, use o binômio negativo.
Distribuição binomial negativa versus distribuição binomial negativa. Distribuição de Poisson
A distribuição de Poisson é frequentemente comparada à binomial negativa ao modelar dados de contagem. Ambos lidam com eventos discretos, mas diferem em suas suposições de variação. A característica que define a distribuição de Poisson é que sua média é igual à sua variância. No entanto, os dados de contagem do mundo real frequentemente apresentam dispersão excessiva, em que a variação excede a média. A distribuição binomial negativa acomoda naturalmente essa variabilidade extra, tornando-a mais adequada para fenômenos como:
- Padrões de surtos de doenças em que alguns casos levam a muitas outras infecções
- Dados de reclamações de clientes em que alguns problemas geram várias reclamações relacionadas
- Picos de tráfego no site em que determinados eventos causam níveis elevados de atividade
Distribuição binomial negativa vs. distribuição geométrica
A distribuição geométrica surge como um caso especial da binomial negativa quando definimos r=1, o que significa que estamos esperando por apenas um sucesso. Isso o torna perfeito para modelar cenários como:
- Número de tentativas até o primeiro sucesso
- Tempo até a primeira falha no teste de confiabilidade
- Número de testes até o primeiro avanço na pesquisa
Distribuição binomial negativa como uma mistura Gamma-Poisson
Por fim, a binomial negativa pode ser derivada como uma mistura Gamma-Poisson, fornecendo uma base teórica para sua capacidade de lidar com a superdispersão. Essa relação ajuda a explicar por que a distribuição binomial negativa funciona bem em modelos hierárquicos em que as taxas de ocorrência individuais variam de acordo com uma distribuição gama.
Vantagens e limitações
A distribuição binomial negativa oferece vantagens distintas que a tornam valiosa para modelar fenômenos do mundo real, além de ter limitações importantes que os cientistas de dados devem considerar.
| Vantagens | Limitações |
|---|---|
| Lida de forma flexível com dados superdispersos quando a variação excede a média | Requer independência entre testes/eventos |
| Os parâmetros têm interpretações claras para uso prático | A estimativa de parâmetros não é confiável com amostras pequenas |
| Acomoda contagens e proporções | Computacionalmente mais intensivo do que as distribuições mais simples |
| Modela naturalmente o agrupamento em dados de contagem | Pode ter um ajuste excessivo quando os dados não estão realmente dispersos |
| Funciona bem com séries temporais e dados longitudinais | Pressupõe uma probabilidade constante de sucesso em todas as tentativas |
Regressão binomial negativa
A regressão binomial negativa amplia a regressão tradicional para dados de contagem, especialmente quando os dados apresentam dispersão excessiva. Enquanto a regressão de Poisson pressupõe que a média é igual à variância, a regressão binomial negativa relaxa essa restrição, tornando-a mais adequada para aplicações no mundo real.
Considere um cenário de call center: Queremos prever o número de chamadas de atendimento ao cliente por hora. Nossos preditores podem incluir:
- Hora do dia
- Dia da semana
- Status do feriado
- Atividade de campanha de marketing
- Condições climáticas
A regressão de Poisson padrão pode subestimar a variação nos volumes de chamadas, especialmente durante os horários de pico ou eventos especiais. A regressão binomial negativa leva em conta essa variabilidade extra, fornecendo previsões e intervalos de confiança mais realistas.
Conclusão
Por sua capacidade de modelar dados de contagem complexos e lidar com a dispersão excessiva, a distribuição binomial negativa continua sendo uma ferramenta essencial para entender e prever fenômenos do mundo real. Como você viu, ele é excelente na modelagem de dados superdispersos, oferece flexibilidade para modelar um grande número de cenários diferentes e se estende naturalmente até a análise de regressão.
Se você estiver interessado em aprofundar seu conhecimento sobre distribuições de probabilidade e suas aplicações, nossos cursos de Probabilidade e Estatística oferecem uma cobertura abrangente desses tópicos. Nossos cursos incluem exercícios práticos com conjuntos de dados do mundo real, ajudando você a dominar os conceitos teóricos e as implementações práticas em Python e R. Além disso, considere nosso curso de carreira de Cientista de Aprendizado de Máquina em Python. Prometo que você aprenderá muito.
Como um profissional experiente em ciência de dados, machine learning e IA generativa, Vinod se dedica a compartilhar conhecimento e capacitar aspirantes a cientistas de dados para que tenham sucesso nesse campo dinâmico.
Perguntas e respostas sobre a distribuição binomial negativa
O que é a distribuição binomial negativa?
A distribuição binomial negativa modela o número de tentativas necessárias para obter um número específico de sucessos em uma sequência de tentativas Bernoulli independentes e identicamente distribuídas.
Como a distribuição binomial negativa difere da distribuição de Poisson?
A distribuição binomial negativa leva em conta a dispersão excessiva em dados de contagem, ao contrário da distribuição de Poisson, que pressupõe média e variação iguais.
Quais são os parâmetros da distribuição binomial negativa?
Os principais parâmetros são o número de sucessos (r) e a probabilidade de sucesso (p) em cada tentativa.
Quando devo usar a distribuição binomial negativa?
Use-o ao modelar dados de contagem com dispersão excessiva, em que a variação excede a média.
Qual é a função de massa de probabilidade da distribuição binomial negativa?
O PMF fornece a probabilidade de você obter um número específico de sucessos em um determinado número de tentativas.
Como faço para calcular as probabilidades usando a distribuição binomial negativa?
Use a fórmula PMF ou um software estatístico para calcular as probabilidades com base nos parâmetros da distribuição.
O que é superdispersão em dados de contagem?
A superdispersão ocorre quando a variância dos dados de contagem excede a média, geralmente abordada pela distribuição binomial negativa.



