Árboles de decisión en aprendizaje automático con R

Imagínese navegando por un laberinto. A cada paso, te enfrentas a una decisión que te acerca a la salida o te adentra más en el laberinto. Se trata de un algoritmo similar a un árbol de decisión, un método de aprendizaje automático potente e intuitivo que nos ayuda a dar sentido a datos complejos y a elegir el mejor curso de acción.

Un algoritmo de árbol de decisión descompone un conjunto de datos en subconjuntos cada vez más pequeños en función de determinadas condiciones. Como un árbol ramificado con hojas y nodos, comienza con un único nodo raíz y se expande en múltiples ramas, cada una de las cuales representa una decisión basada en el valor de una característica. Las hojas finales del árbol son los posibles resultados o predicciones.

Este artículo le introducirá en el mundo de los árboles de decisión utilizando el lenguaje de programación R. Discutiremos los conceptos básicos, nos sumergiremos en los tipos más populares de algoritmos de árboles de decisión, exploraremos métodos basados en árboles y le guiaremos a través de un ejemplo paso a paso. Al final, será capaz de aprovechar el poder de los árboles de decisión para tomar mejores decisiones basadas en datos.

¿Qué es un árbol de decisión en el aprendizaje automático?

Los árboles de decisión son especiales en el aprendizaje automático debido a su simplicidad, interpretabilidad y versatilidad.

Se trata de un algoritmo de aprendizaje automático supervisado que puede utilizarse tanto para problemas de regresión (predicción de valores continuos) como de clasificación (predicción de valores categóricos). Además, sirven de base para técnicas más avanzadas, como bagging, boosting y bosques aleatorios.

Este diagrama ilustra la terminología de los árboles de decisión:

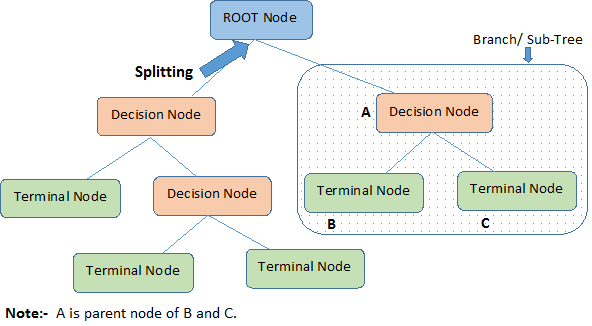
Un árbol de decisión comienza con un nodo raíz que significa toda la población o muestra, que luego se separa en dos o más grupos uniformes mediante un método denominado división. Cuando los subnodos sufren una nueva división, se identifican como nodos de decisión, mientras que los que no se dividen se denominan nodos terminales u hojas. Un segmento de un árbol completo se denomina rama.

Establecimos que los árboles de decisión podían utilizarse tanto para tareas de regresión como de clasificación; por lo tanto, entendamos el algoritmo que hay detrás de los tipos de árboles de decisión.

Tipos populares de algoritmos de árboles de decisión

Comprendamos intuitivamente los árboles de decisión de regresión y de clasificación, en qué se parecen y en qué se diferencian, y las funciones de error.

Árboles de regresión

Veamos la imagen siguiente, que ayuda a visualizar la naturaleza de la partición realizada por un Árbol de Regresión. Muestra un árbol sin podar y un árbol de regresión ajustado a un conjunto de datos aleatorio. Ambas visualizaciones muestran una serie de reglas de división, empezando por la parte superior del árbol. Observe que cada división del dominio está alineada con uno de los ejes de características. El concepto de división paralela al eje se generaliza directamente a dimensiones superiores a dos. Para un espacio de características de tamaño $p$, un subconjunto de $\mathbb{R}^p$, el espacio se divide en $M$ regiones, $R_{m}$, cada una de las cuales es un "hiperbloque" de dimensión $p$.

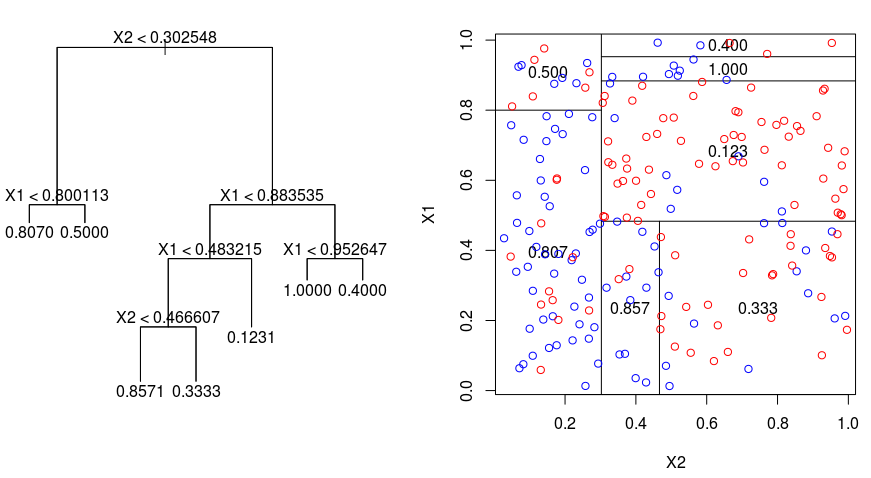
Para construir un árbol de regresión, primero se utiliza la división binaria recursiva para hacer crecer un árbol grande en los datos de entrenamiento, deteniéndose sólo cuando cada nodo terminal tiene menos de un número mínimo de observaciones. La división binaria recursiva es un algoritmo codicioso y descendente utilizado para minimizar la suma residual de cuadrados (RSS), una medida de error también utilizada en entornos de regresión lineal. El RSS, en el caso de un espacio de características particionado con M particiones, viene dado por:

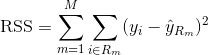
Comenzando en la parte superior del árbol, lo divides en 2 ramas, creando una partición de 2 espacios. A continuación, realice esta división concreta en la parte superior del árbol varias veces y elija la división de las características que minimice el RSS (actual).

A continuación, se aplica la poda de complejidad de costes al árbol grande para obtener una secuencia de los mejores subárboles, en función de $\alpha$. La idea básica aquí es introducir un parámetro de ajuste adicional, denotado por $\alpha$ que equilibra la profundidad del árbol y su bondad de ajuste a los datos de entrenamiento.

Puede utilizar la validación cruzada K-fold para elegir $\alpha$. Esta técnica consiste simplemente en dividir las observaciones de entrenamiento en K pliegues para estimar la tasa de error de prueba de los subárboles. Su objetivo es seleccionar el que conduzca a la tasa de error más baja.

Árboles de clasificación

Un árbol de clasificación es muy similar a un árbol de regresión, salvo que se utiliza para predecir una respuesta cualitativa en lugar de una cuantitativa.

Recordemos que para un árbol de regresión, la respuesta prevista para una observación viene dada por la respuesta media de las observaciones de entrenamiento que pertenecen al mismo nodo terminal. En cambio, en un árbol de clasificación, se predice que cada observación pertenece a la clase más frecuente de las observaciones de entrenamiento en la región a la que pertenece.

Al interpretar los resultados de un árbol de clasificación, a menudo se está interesado no sólo en la predicción de clase correspondiente a una región de nodo terminal en particular, sino también en las proporciones de clase entre las observaciones de entrenamiento que caen en esa región.

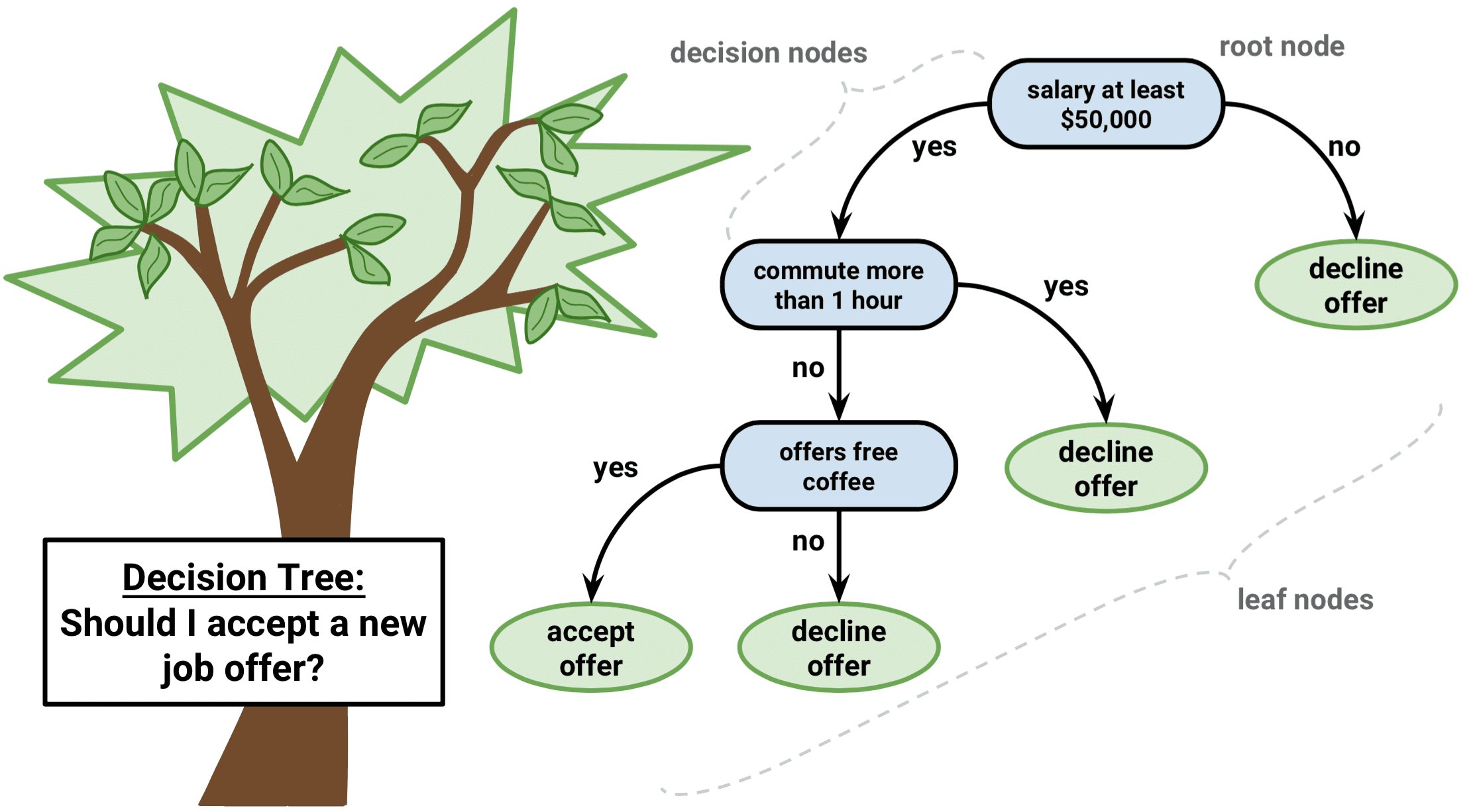
La tarea de hacer crecer un árbol de clasificación es bastante similar a la tarea de hacer crecer un árbol de regresión. Al igual que en la configuración de regresión, se utiliza la división binaria recursiva para hacer crecer un árbol de clasificación. Sin embargo, en el ámbito de la clasificación, la suma residual de cuadrados no puede utilizarse como criterio para realizar las divisiones binarias. En su lugar, puede utilizar cualquiera de estos 3 métodos que se indican a continuación:

• Tasa de error de clasificación: En lugar de ver cuánto se aleja una respuesta numérica del valor medio, como en la configuración de regresión, puede definir la "tasa de aciertos" como la fracción de observaciones de entrenamiento en una región concreta que no pertenece a la clase más frecuente. El error viene dado por esta ecuación:

E = 1 - argmax_c($\hat{\pi}_{mc}$)

en la que $\hat{\pi}_{mc}$ representa la fracción de datos de entrenamiento en la región _Rm que pertenecen a la clase c.

• Gini Index: El Índice de Gini es una métrica de error alternativa diseñada para mostrar lo "pura" que es una región. En este caso, "pureza" significa cuántos de los datos de entrenamiento de una región concreta pertenecen a una única clase. Si una región _Rm contiene datos que proceden mayoritariamente de una única clase c, el valor del Índice de Gini será pequeño:

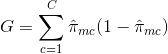
• Entropía cruzada: Una tercera alternativa, similar al índice de Gini, se conoce como entropía cruzada o desviación:

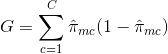
La entropía cruzada tomará un valor cercano a cero si los $\hat{\pi}_{mc}$ son todos cercanos a 0 o cercanos a 1. Por lo tanto, al igual que el índice de Gini, la entropía cruzada tomará un valor pequeño si el m-ésimo nodo es puro. De hecho, resulta que el índice de Gini y la entropía cruzada son bastante similares numéricamente.

Cuando se construye un árbol de clasificación, se suele utilizar el índice de Gini o la entropía cruzada para evaluar la calidad de una división concreta, ya que son más sensibles a la pureza de los nodos que la tasa de error de clasificación. Cualquiera de estos 3 enfoques podría utilizarse al podar el árbol, pero la tasa de error de clasificación es preferible si el objetivo es la precisión de predicción del árbol podado final.

Ventajas y desventajas de los árboles de decisión

Por mucho que nos gustaría entender el algoritmo y sus puntos fuertes, es crucial comprender sus defectos. La verdad es que los árboles de decisión no son los más adecuados para todos los tipos de algoritmos de aprendizaje automático, lo que también ocurre con todos los algoritmos de aprendizaje automático.

He aquí las ventajas y los inconvenientes:

Advantages

1. Fácil de entender e interpretar. Los árboles de decisión son muy intuitivos y pueden visualizarse fácilmente. Su estructura jerárquica se asemeja a la toma de decisiones humana, lo que las hace accesibles incluso a los no expertos. Esta interpretabilidad es crucial en situaciones en las que comprender el proceso de decisión es tan importante como la propia predicción.
2. Puede manejar tanto variables continuas como categóricas. Los árboles de decisión son versátiles y pueden gestionar conjuntos de datos con una mezcla de características continuas y categóricas, así como variables objetivo de ambos tipos. Esta flexibilidad permite aplicar los árboles de decisión a una amplia gama de problemas.
3. Se requiere un preprocesamiento mínimo de los datos. Los árboles de decisión no requieren escalado o normalización de características, ya que son invariables a las transformaciones monotónicas. También pueden manejar fácilmente valores perdidos y valores atípicos, por lo que son adecuados para datos brutos y ruidosos.
4. Puede utilizarse para seleccionar características e identificar variables importantes. Los árboles de decisión realizan de forma natural la selección de características eligiendo las más informativas para dividir los datos. La importancia de una característica puede determinarse en función de lo pronto que aparezca en el árbol y de la frecuencia con que se utilice para la división.

Disadvantages

1. Propenso al sobreajuste. Los árboles de decisión pueden volverse demasiado complejos cuando crecen en profundidad, lo que lleva a sobreajustar los datos de entrenamiento. El resultado es una mala generalización de los datos no vistos. Técnicas como la poda o el establecimiento de una profundidad máxima pueden ayudar a mitigar este problema.
2. Sensible a pequeños cambios en los datos. Un pequeño cambio en los datos de entrenamiento puede dar lugar a una estructura de árbol completamente diferente, lo que hace que los árboles de decisión sean inestables. Esta sensibilidad puede reducirse mediante métodos de conjunto, como bagging, boosting o random forests, que construyen múltiples árboles y agregan sus resultados.
3. Los modelos de árboles de decisión no suelen ser tan precisos como otros métodos de aprendizaje automático. Debido a su simplicidad y a la naturaleza codiciosa de su construcción, los árboles de decisión no siempre producen los modelos más precisos. Sin embargo, pueden servir como buen punto de partida o modelo de referencia para comparar con métodos más sofisticados.
4. Sesgo hacia las clases dominantes. Los árboles de decisión pueden estar sesgados hacia la clase mayoritaria en conjuntos de datos desequilibrados, lo que conduce a divisiones subóptimas y a la clasificación errónea de instancias minoritarias. Técnicas como el sobremuestreo, el submuestreo o el aprendizaje sensible a los costes pueden ayudar a resolver este problema.

A pesar de estas desventajas, los árboles de decisión siguen siendo una opción popular en muchas aplicaciones debido a su simplicidad, interpretabilidad y versatilidad.

Algoritmos avanzados de aprendizaje automático basado en árboles

Exploremos los métodos ensemble basados en árboles que aprovechan los puntos fuertes de los árboles de decisión al tiempo que abordan algunas de sus limitaciones: bagging, boosting y bosques aleatorios.

Embolsado

Los árboles de decisión mencionados anteriormente presentan una varianza elevada, lo que significa que si se dividen los datos de entrenamiento en dos partes al azar y se aplica un árbol de decisión a ambas mitades, los resultados obtenidos pueden ser muy diferentes. Por el contrario, un procedimiento con baja varianza arrojará resultados similares si se aplica repetidamente a un conjunto de datos distinto.

El ensacado, o agregación bootstrap, es una técnica utilizada para reducir la varianza de sus predicciones combinando el resultado de múltiples clasificadores modelados en diferentes submuestras del mismo conjunto de datos. He aquí la ecuación para el embolsado:

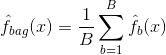
en el que se generan $B$ conjuntos de datos de entrenamiento bootstrapped diferentes. A continuación, entrenar su método en el $bth$ bootstrapped conjunto de entrenamiento con el fin de obtener $\hat{f}_{b}(x)$, y, finalmente, el promedio de las predicciones.

El siguiente gráfico muestra las tres fases del embolsado:

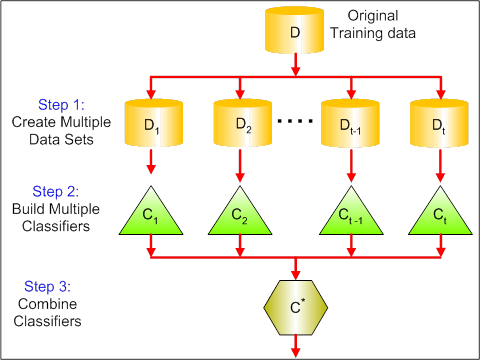
• Paso 1: Aquí se sustituyen los datos originales por otros nuevos. Los nuevos datos suelen tener una fracción de las columnas y filas de los datos originales, que luego pueden utilizarse como hiperparámetros en el modelo de bagging.

• Segundo paso: Se construyen clasificadores en cada conjunto de datos. Por lo general, se puede utilizar el mismo clasificador para realizar modelos y predicciones.

• Tercer paso: Por último, se utiliza un valor medio para combinar las predicciones de todos los clasificadores, en función del problema. En general, estos valores combinados son más sólidos que un modelo único.

Aunque el ensacado puede mejorar las predicciones de muchos métodos de regresión y clasificación, es especialmente útil para los árboles de decisión. Para aplicar bagging a árboles de regresión/clasificación, simplemente se construyen $B$ árboles de regresión/clasificación utilizando $B$ conjuntos de entrenamiento bootstrapped, y se promedian las predicciones resultantes. Estos árboles crecen en profundidad y no se podan. De ahí que cada árbol individual tenga una varianza alta, pero un sesgo bajo. El promedio de estos árboles $B$ reduce la varianza.

En términos generales, se ha demostrado que el ensacado proporciona impresionantes mejoras de precisión al combinar cientos o incluso miles de árboles en un único procedimiento.

Bosques aleatorios

Los bosques aleatorios son un método versátil de aprendizaje automático capaz de realizar tareas tanto de regresión como de clasificación. También lleva a cabo métodos de reducción dimensional, trata los valores perdidos, los valores atípicos y otros pasos esenciales de la exploración de datos, y hace un trabajo bastante bueno.

Los bosques aleatorios mejoran los árboles empaquetados mediante un pequeño ajuste que decorrelaciona los árboles. Como en el bagging, se construyen varios árboles de decisión a partir de muestras de entrenamiento bootstrapped. Pero cuando se construyen estos árboles de decisión, cada vez que se considera una división en un árbol, se elige una muestra aleatoria de m pred ictores como candidatos a la división del conjunto completo de $p$ predictores. La división sólo puede utilizar uno de esos $m$ predictores. Esta es la principal diferencia entre los bosques aleatorios y el ensacado; porque como en el ensacado, la elección del predictor $m = p$.

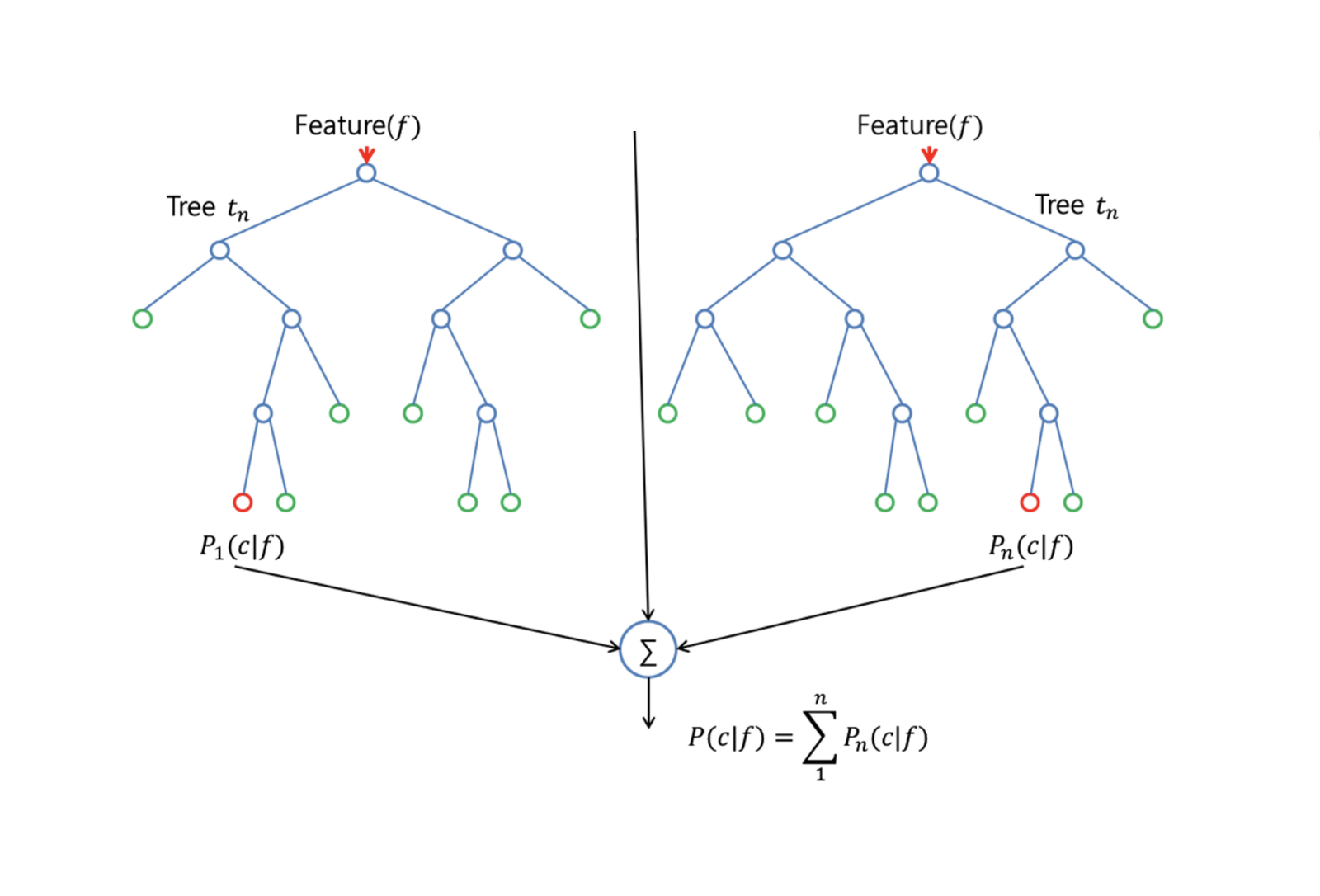
Para hacer crecer un bosque aleatorio, debes:

• En primer lugar, supongamos que el número de casos del conjunto de entrenamiento es K. A continuación, tomemos una muestra aleatoria de estos K casos y utilicemos esta muestra como conjunto de entrenamiento para hacer crecer el árbol.

• Si hay $p$ variables de entrada, especifique un número $m < p$ tal que en cada nodo pueda seleccionar $m$ variables aleatorias de entre las $p$. La mejor división en estos $m$ se utiliza para dividir el nodo.

• Posteriormente, cada árbol crece lo máximo posible y no es necesario podarlo.

• Por último, agrega las predicciones de los árboles objetivo para predecir nuevos datos.

Random Forests es muy eficaz para estimar los datos que faltan y mantener la precisión cuando falta una gran proporción de los datos. También puede equilibrar errores en conjuntos de datos en los que las clases están desequilibradas. Y lo que es más importante, puede manejar conjuntos de datos masivos con una gran dimensionalidad. Sin embargo, una de las desventajas de los bosques aleatorios es que pueden sobreajustarse fácilmente conjuntos de datos ruidosos, especialmente en el caso de la regresión.

Impulsar

El refuerzo es otro método para mejorar las predicciones resultantes de un árbol de decisión. Al igual que el bagging y los bosques aleatorios, es un enfoque general que puede aplicarse a muchos métodos de aprendizaje estadístico para la regresión o la clasificación. Recordemos que el bagging consiste en crear múltiples copias del conjunto de datos de entrenamiento original utilizando el bootstrap, ajustar un árbol de decisión distinto a cada copia y, a continuación, combinar todos los árboles para crear un único modelo predictivo. En particular, cada árbol se construye a partir de un conjunto de datos bootstrapped, independiente de los demás árboles.

El refuerzo funciona de forma similar, salvo que los árboles crecen secuencialmente: cada árbol crece utilizando la información de los árboles crecidos anteriormente. El refuerzo no implica un muestreo bootstrap, sino que cada árbol se ajusta a una versión modificada del conjunto de datos original.

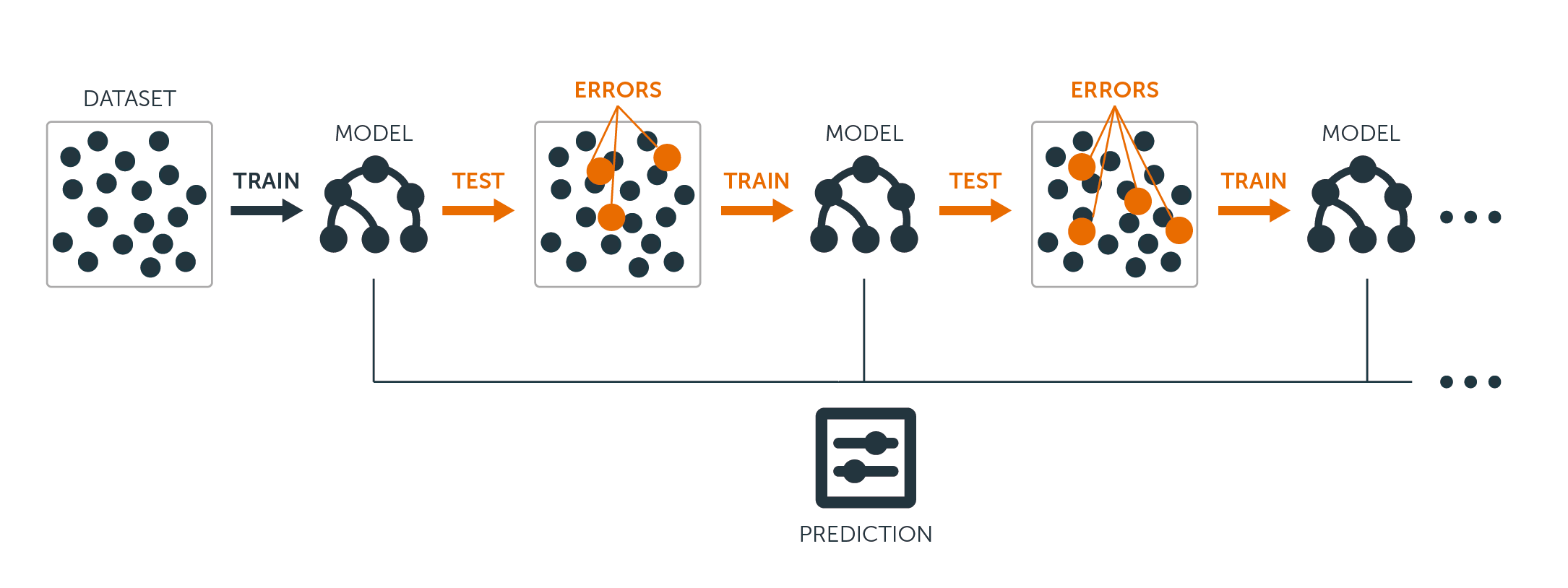
Tanto para los árboles de regresión como para los de clasificación, el boosting funciona así:

• A diferencia de ajustar un único árbol de decisión de gran tamaño a los datos, lo que equivale a ajustar los datos al máximo y potencialmente sobreajustarlos, el enfoque de refuerzo aprende lentamente.

• Dado el modelo actual, se ajusta un árbol de decisión a los residuos del modelo. Es decir, se ajusta un árbol utilizando los residuos actuales, en lugar del resultado $Y$, como respuesta.

• A continuación, añada este nuevo árbol de decisión a la función ajustada para actualizar los residuos. Cada uno de estos árboles puede ser bastante pequeño, con sólo unos pocos nodos terminales, determinados por el parámetro $d$ del algoritmo. Ajustando pequeños árboles a los residuos, se mejora lentamente $\hat{f}$ en las áreas donde no funciona bien.

• El parámetro de contracción $\nu$ ralentiza aún más el proceso, permitiendo que más árboles y de formas diferentes ataquen a los residuos.

El refuerzo es muy útil cuando se dispone de muchos datos y se espera que los árboles de decisión sean muy complejos. El boosting se ha utilizado para resolver muchos problemas de clasificación y regresión, como el análisis de riesgos, el análisis de sentimientos, la publicidad predictiva, la modelización de precios, la estimación de ventas y el diagnóstico de pacientes, entre otros.

Básicamente, estos algoritmos combinan las predicciones de varios árboles de decisión para mejorar el rendimiento y la estabilidad generales. Una vez comprendidos los algoritmos avanzados, para el ámbito de este tutorial, procederemos con los modelos de árboles de decisión sencillos.

Creación de modelos de árbol de decisión paso a paso en R

Hemos aprendido mucha teoría y la intuición que hay detrás de los modelos de árboles de decisión y sus variaciones, pero no hay nada como ponerse manos a la obra y construir esos modelos, evaluando su rendimiento paso a paso.

Preparación de los datos para la modelización

Para los siguientes ejemplos, utilizaremos el popular Boston Housing Dataset.

El conjunto de datos Boston Housing contiene información sobre el mercado de la vivienda en Boston, Massachusetts, en la década de 1970. Cuenta con 506 observaciones y 14 variables, entre ellas 13 características y 1 variable objetivo.

Las características del conjunto de datos Boston Housing son:

• CRIM: Índice de delincuencia per cápita por ciudad
• ZN: Proporción de suelo residencial zonificado para lotes de más de 25.000 pies cuadrados.
• INDUS: Proporción de acres comerciales no minoristas por ciudad
• CHAS: Variable ficticia Charles River (= 1 si el tramo linda con el río; 0 en caso contrario)
• NOX: Concentración de óxido nítrico (partes por 10 millones)
• RM: Número medio de habitaciones por vivienda
• AGE: Proporción de unidades ocupadas por sus propietarios construidas antes de 1940
• DIS: Distancias ponderadas a cinco centros de empleo de Boston
• RAD: Índice de accesibilidad a las autopistas radiales
• TAX: Tipo del impuesto sobre bienes inmuebles de valor íntegro por 10.000 dólares
• PTRATIO: Ratio alumnos-profesor por ciudad
• Negros: proporción de población negra por ciudad
• LSTAT: Porcentaje de la población de estatus más bajo

La variable objetivo es el MEDV, que representa el valor medio de las viviendas ocupadas por sus propietarios en miles de dólares.

El objetivo es predecir el valor medio de las viviendas ocupadas por sus propietarios (en miles de dólares) basándose en las características dadas.

En R, los datos se proporcionan en un paquete llamado "MASS". Tendrás que instalar varios paquetes para este tutorial y cargarlos. Como esto sería una repetición, vamos a demostrar este proceso con el paquete MASS una vez, y lo repetirás cada vez que veas un nuevo paquete utilizado en esta guía.

# install the package
install.packages("MASS")

# Load the MASS package
library(MASS)

# Load the Boston Housing dataset
data(Boston)

A menudo es necesario explorar los datos mediante visualizaciones y realizar pasos de preprocesamiento de datos antes de pasar a la modelización. Veamos la distribución de las variables mediante histogramas.

Aquí está el código para crearlos:

# Load the library
library(tidymodels)
library(tidyr)

# Prepare the dataset for ggplot2
boston_data_long <- Boston %>%
 pivot_longer(cols = everything(),
              names_to = "variable",
              values_to = "value")

# Create a histogram for all numeric variables in one plot
boston_histograms <- ggplot(boston_data_long, aes(x = value)) +
 geom_histogram(bins = 30, color = "black", fill = "lightblue") +
 facet_wrap(~variable, scales = "free", ncol = 4) +
 labs(title = "Histograms of Numeric Variables in the Boston Housing Dataset",
      x = "Value",
      y = "Frequency") +
 theme_minimal()

# Plot the histograms
print(boston_histograms)

Y la salida tiene este aspecto:

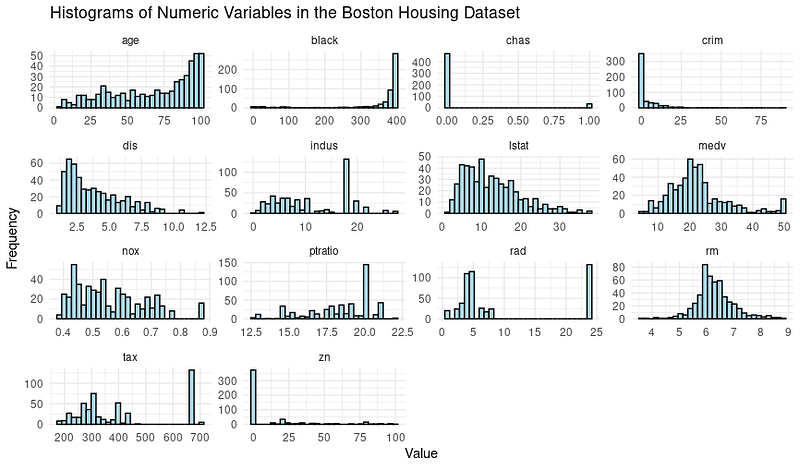
Observamos algunos valores atípicos, especialmente en columnas como RAD, TAX y NOX. Nuestro objetivo en este tutorial es centrarnos en la fase de modelado del árbol de decisión, por lo que vamos a dividir el conjunto de datos en conjuntos de entrenamiento y de prueba.

# Split the data into training and testing sets

set.seed(123)
data_split <- initial_split(Boston, prop = 0.75)
train_data <- training(data_split)
test_data <- testing(data_split)

Pasemos ahora a la modelización y la evaluación del rendimiento del modelo.

Árbol de decisión simple

Utilizando la función decision_tree() del paquete Tidymodels en R, resulta sencillo crear primero la especificación de un modelo de árbol de decisión y, a continuación, ajustar el modelo a los datos de entrenamiento.

# Create a decision tree model specification
tree_spec <- decision_tree() %>%
 set_engine("rpart") %>%
 set_mode("regression")

# Fit the model to the training data
tree_fit <- tree_spec %>%
 fit(medv ~ ., data = train_data)

Aquí utilizamos el modelo de "regresión", y para un árbol de decisión de clasificación, tendríamos que utilizar el modo de "clasificación".

Evaluación del rendimiento del modelo Decision Treel

Para evaluar el rendimiento del modelo, utilizaremos el paquete Tidymodels para calcular el error cuadrático medio (RMSE) y el valor R-cuadrado de nuestro modelo de árbol de decisión en los datos de prueba.

# Make predictions on the testing data
predictions <- tree_fit %>%
 predict(test_data) %>%
 pull(.pred)

# Calculate RMSE and R-squared
metrics <- metric_set(rmse, rsq)
model_performance <- test_data %>%
 mutate(predictions = predictions) %>%
 metrics(truth = medv, estimate = predictions)

print(model_performance)

Obtendrás una salida que presenta dos métricas de rendimiento: Error cuadrático medio (RMSE) y R cuadrado (R²).

 .metric .estimator .estimate
 <chr>   <chr>          <dbl>
1 rmse    standard       5.22
2 rsq     standard       0.689

Análisis de los resultados del modelo

Entonces, ¿son suficientemente buenos los resultados de nuestro modelo?

• RMSE (error cuadrático medio): Mide la diferencia media entre los valores previstos y los reales. En su caso, el RMSE es de 5,22, lo que significa que, de media, las predicciones realizadas por el modelo de árbol de decisión se alejan aproximadamente 5,22 unidades de los valores reales. Un valor de RMSE más bajo suele ser mejor, ya que indica menores errores de predicción.
• R-cuadrado (R²): Mide hasta qué punto el modelo explica la varianza de la variable objetivo. Oscila entre 0 y 1, y un valor más alto indica un mejor ajuste. En su caso, la R² es de 0,689, lo que significa que el modelo explica aproximadamente el 68,9% de la varianza de la variable objetivo (MEDV).

También podemos optimizar los hiperparámetros para exprimir el rendimiento o apostar por modelos más complejos como Random Forests y XGBoost a costa de la interpretabilidad del modelo.

Predicción de resultados mediante el modelo de árbol de decisión

Una vez que estés satisfecho con el modelo, es hora de dejar que haga predicciones.

Esto es lo mismo que hicimos con los datos de prueba utilizando la función predict(), pero tendremos que proporcionar un nuevo conjunto de datos que imiten la información sobre una casa nueva en Boston. Es un escenario posible cuando el modelo se ponga en marcha en un entorno de producción.

# Make predictions on new data
new_data <- tribble(
 ~crim, ~zn, ~indus, ~chas, ~nox, ~rm, ~age, ~dis, ~rad, ~tax, ~ptratio, ~black, ~lstat,
 0.03237, 0, 2.18, 0, 0.458, 6.998, 45.8, 6.0622, 3, 222, 18.7, 394.63, 2.94
)
predictions <- predict(tree_fit, new_data)
print(predictions)

Y obtendrás el valor medio previsto (en miles de dólares) de esta casa en concreto:

# A tibble: 1 × 1
 .pred
 <dbl>
1  37.8

Ahora vamos a centrarnos en cómo podemos interpretar lo que ocurre dentro del modelo para nosotros mismos y para las partes interesadas que utilizan la solución que acabamos de crear.

Interpretación del árbol de decisión

La ventaja más significativa, como ya hemos dicho, es la interpretabilidad de los modelos de árbol de decisión. Visualicemos el árbol de decisión para comprender mejor el modelo:

# Load the library
library(rpart.plot)

# Plot the decision tree
rpart.plot(tree_fit$fit, type = 4, extra = 101, under = TRUE, cex = 0.8, box.palette = "auto")

Verás una trama como ésta:

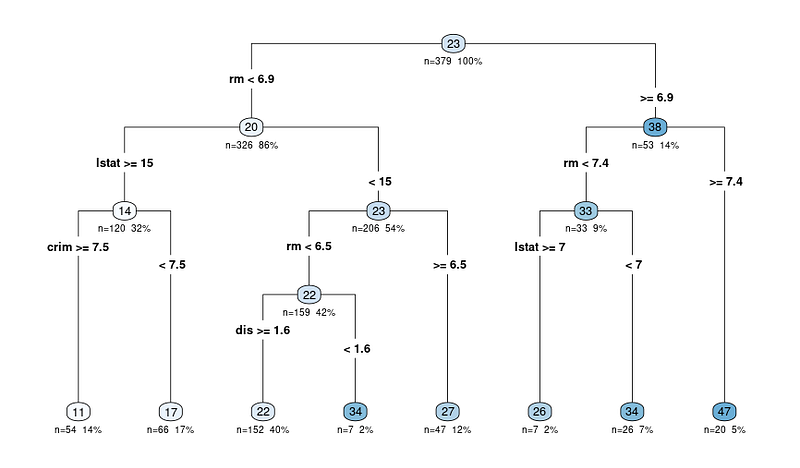
El diagrama de salida de la función rpart.plot muestra una representación del modelo en forma de árbol de decisión. En este diagrama, cada nodo representa una división en el árbol de decisión basada en las variables predictoras. El diagrama de salida incluye varios datos que pueden ayudarnos a interpretar el árbol de decisión:

Los diagramas de árbol comienzan con el nodo

Los nodos están representados por círculos y conectados por líneas, lo que muestra la estructura jerárquica del árbol de decisión. El árbol comienza con un nodo raíz en la parte superior y se ramifica en nodos internos que, en última instancia, conducen a los nodos terminales u hojas en la parte inferior.

Los criterios de división de cada nodo interno

Cada nodo interno muestra el criterio de división, que es la variable de predicción y el valor utilizado para dividir los datos en dos subconjuntos.

Por ejemplo, un nodo puede mostrar "RM < 6,8", lo que indica que las observaciones con un número medio de habitaciones por vivienda (RM) inferior a 6,8 seguirán la rama izquierda, mientras que las observaciones con RM igual o superior a 6,8 seguirán la rama derecha.

N: Número de observaciones después de la división

El valor n de cada nodo representa el número de observaciones del conjunto de datos que entran en ese nodo concreto. Por ejemplo, si un nodo muestra "n = 100", significa que 100 observaciones del conjunto de datos cumplen los criterios de los nodos padre de ese nodo.

X%: Proporción de las observaciones totales del conjunto de datos que llegaron al nodo en cuestión.

El valor porcentual le ayuda a comprender el tamaño relativo de cada nodo en comparación con el conjunto de datos completo, mostrando cómo se están dividiendo y distribuyendo los datos en el árbol. Un porcentaje más alto significa que una mayor proporción de los datos ha seguido la ruta de decisión que lleva al nodo específico, mientras que un porcentaje más bajo indica una menor proporción de los datos que llegan a ese nodo.

El valor previsto para cada nodo

El valor previsto en cada nodo se muestra como un número dentro de un círculo de color (nodo). En un árbol de regresión, es el valor medio de la variable objetivo para todas las observaciones que entran en ese nodo.

Por ejemplo, el último nodo principal que muestra 47 significa que el valor medio de la variable objetivo (en nuestro caso, el valor medio de las viviendas ocupadas por sus propietarios) para todas las observaciones de ese nodo es 47.

Empieza en el nodo raíz y sigue las ramas

Por tanto, al interpretar cualquier resultado, se empieza en el nodo raíz y se siguen las ramas en función de los criterios de división hasta llegar a un nodo terminal. El valor predicho en el nodo terminal da la predicción del modelo para una observación dada y la justificación de la decisión.

Extracción de las reglas del árbol de decisión

Si aún así prefiere extraer las reglas en forma de texto (en lugar de recorrer el diagrama), también puede hacerlo utilizando la misma biblioteca que utilizamos para trazar el diagrama.

Aquí está el código para hacerlo:

rules <- rpart.rules(tree_fit$fit)
print(rules)

Y verás una salida con los valores predichos y las reglas que sigue para llegar a ese valor, como se indica a continuación:

medv                                                              
  11 when rm <  6.9        & lstat >= 15 & crim >= 7.5            
  17 when rm <  6.9        & lstat >= 15 & crim <  7.5            
  22 when rm <  6.5        & lstat <  15               & dis >= 1.6
  26 when rm is 6.9 to 7.4 & lstat >=  7                          
  27 when rm is 6.5 to 6.9 & lstat <  15                          
  34 when rm <  6.5        & lstat <  15               & dis <  1.6
  34 when rm is 6.9 to 7.4 & lstat <   7                          
  47 when rm >=        7.4

Ahora que ve las reglas, puede que se pregunte cómo se puede tomar la decisión con 3-4 variables cuando introducimos muchas más variables en el árbol de decisión.

Bueno, resulta que algunas variables son más importantes que el resto. Entendamos mejor este concepto.

Comprender las variables importantes de los árboles de decisión

Ya hemos desvelado el diagrama de árbol y cómo funciona el modelo. Un último aspecto de la interpretación es comprender las variables importantes del conjunto de datos.

He aquí por qué es crucial:

• Selección de características. Identificar las variables importantes puede ayudarle a centrarse en las características relevantes y a eliminar potencialmente las menos importantes, simplificando su modelo y reduciendo el ruido.
• Conocimiento del ámbito. Conocer qué características son las más importantes puede ayudarle a comprender mejor las relaciones entre las variables y la variable objetivo en el contexto de su problema específico.
• Interpretación del modelo. Comprender las características clave que determinan las predicciones del modelo puede aportar información valiosa para el proceso de toma de decisiones.

En los árboles de decisión, la importancia de las variables suele venir determinada por las características utilizadas para la división en los nodos. Las características que se utilizan para dividir más arriba en el árbol o que se utilizan con más frecuencia pueden considerarse más importantes.

La importancia de una variable puede cuantificarse por la reducción de la medida de impureza (por ejemplo, el índice de Gini o el error cuadrático medio) que aporta cuando se utiliza para la división. El paquete "VIP" de R ha eliminado todas las complejidades, y el gráfico puede obtenerse mediante el código siguiente:

# Load the necessary library
library(vip)

# Create a variable importance plot
var_importance <- vip::vip(tree_fit, num_features = 10)
print(var_importance)

Y obtendrás el gráfico de importancia variable que aparece a continuación:

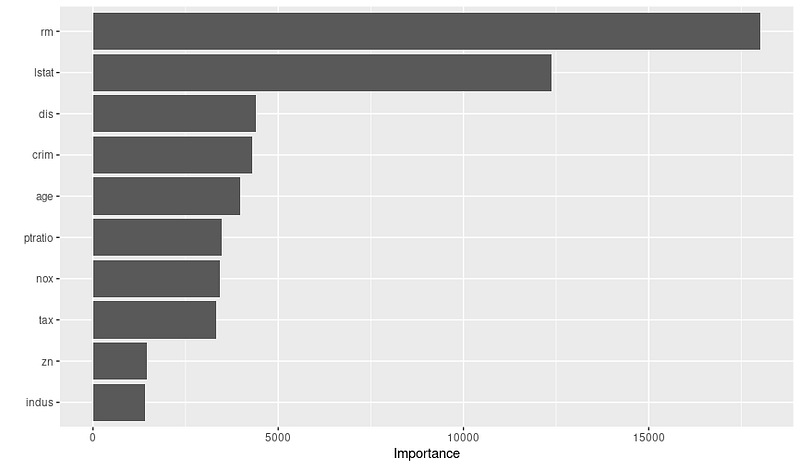
Una vez que veas el gráfico, podrías investigar más a fondo por qué son importantes estas variables, colaborando con expertos en la materia. Por ejemplo, basándonos en el gráfico anterior, podemos deducir las 3 variables más importantes y su justificación:

1. RM: El número medio de habitaciones por vivienda es una característica muy crucial, ya que sugiere que las casas con más habitaciones tienden a tener valores medios más altos.
2. LSTAT: El porcentaje de la población con un estatus socioeconómico más bajo es otra variable significativa, lo que indica que los barrios con un estatus más bajo probablemente tengan valores medios de la vivienda más bajos.
3. DIS: La distancia ponderada a los centros de empleo es una variable vital, que muestra que las viviendas más cercanas a los principales centros de empleo tienen más probabilidades de tener valores medios más altos.

Así que recuerde comprobar el gráfico de importancia de las variables antes de finalizar su modelo; esto puede ayudarle a crear y seleccionar mejores características para optimizar el rendimiento.

Conclusión

En este tutorial, hemos explorado los conceptos fundamentales de los árboles de decisión y abordado no sólo la construcción de modelos, sino también su interpretación. Los árboles de decisión son modelos potentes e interpretables tanto para tareas de clasificación como de regresión, lo que los convierte en una herramienta esencial en el arsenal de un científico de datos.

A medida que continúe desarrollando sus habilidades, le animamos a profundizar en el mundo de los árboles de decisión, explorar algoritmos alternativos y mejorar sus habilidades de programación en R. Aquí tienes algunos recursos para dar el siguiente paso:

• Fundamentos de aprendizaje automático en R
• Introducción a la ingeniería de características en R
• Modelización con Tidymodels en R
• Aprendizaje automático con modelos basados en árboles en R

Sin duda, ampliar sus conocimientos y experimentar con nuevas herramientas y técnicas le permitirá afrontar diversos retos y aportará valiosas perspectivas a sus proyectos.