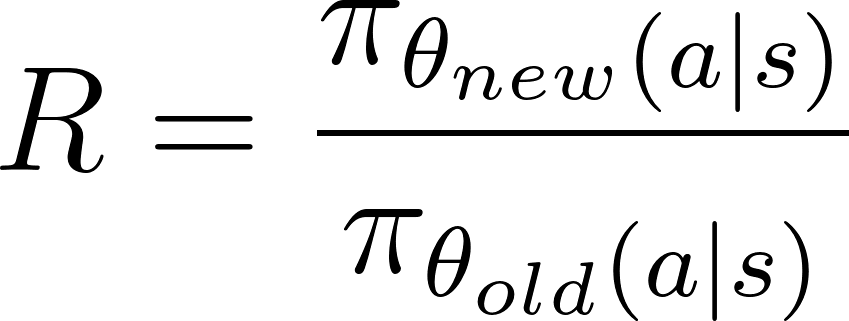Optimización de políticas proximales con PyTorch y Gymnasium

1. Configurar el entorno 

Antes de aplicar la PPO, tenemos que instalar las bibliotecas de software necesarias y elegir un entorno adecuado para aplicar la política. 

Instalar PyTorch y las librerías necesarias 

Necesitamos instalar el siguiente software: 

• PyTorch y otras bibliotecas de software, como numpy (para funciones matemáticas y estadísticas) y matplotlib (para trazar gráficos).
• El paquete de software de código abierto Gym de OpenAI, una biblioteca de Python que simula diferentes entornos y juegos, que pueden resolverse mediante el aprendizaje por refuerzo. Puedes utilizar la API Gimnasio para que tu algoritmo interactúe con el entorno. Como la funcionalidad de gym a veces cambia durante el proceso de actualización, en este ejemplo, congelamos su versión a 0.25.2.

Para instalarlo en un servidor o en una máquina local, ejecuta 

$ pip install torch numpy matplotlib gym==0.25.2

Para instalarlo utilizando un bloc de notas como Google Colabo DataLab, utiliza 

!pip install torch numpy matplotlib gym==0.25.2

Crea el/los entorno/s CartPole

Utiliza OpenAI Gym para crear dos instancias (una para entrenamiento y otra para pruebas) del entorno CartPole:

env_train = gym.make('CartPole-v1')
env_test = gym.make('CartPole-v1')

2. Implementar PPO en PyTorch

Ahora, vamos a implementar PPO utilizando PyTorch.

Definir la red política

Como ya se ha explicado, la OPP se aplica como un modelo actor-crítico. El actor aplica la política, y el crítico predice su valor estimado. Tanto las redes neuronales de actores como las de críticos toman la misma entrada: el estado en cada paso temporal. Así, los modelos de actor y de crítico pueden compartir una red neuronal común, que se denomina arquitectura troncal. El actor y el crítico pueden ampliar la arquitectura troncal con capas adicionales. 

Definir la red troncal

Los siguientes pasos describen la red troncal:

• Implementa una red con 3 capas: una de entrada, una oculta y una de salida. 
• Después de las capas de entrada y oculta, utilizamos una función de activación. En este tutorial, elegimos ReLU porque es computacionalmente eficiente. 
• También imponemos una función de abandono tras las capas de entrada y oculta para obtener una red robusta. La función de abandono pone a cero aleatoriamente algunas neuronas. Esto reduce la dependencia de neuronas concretas y evita el sobreajuste, con lo que la red es más robusta. 

El código siguiente implementa la columna vertebral:

class BackboneNetwork(nn.Module):
    def __init__(self, in_features, hidden_dimensions, out_features, dropout):
        super().__init__()
        self.layer1 = nn.Linear(in_features, hidden_dimensions)
        self.layer2 = nn.Linear(hidden_dimensions, hidden_dimensions)
        self.layer3 = nn.Linear(hidden_dimensions, out_features)
        self.dropout = nn.Dropout(dropout)
    def forward(self, x):
        x = self.layer1(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer2(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer3(x)
        return x

Definir la red actor-crítica

Ahora podemos utilizar esta red para definir la clase actor-crítico, ActorCritic. El actor modela la política y predice la acción. El crítico modela la función de valor y predice el valor. Ambos toman el estado como entrada. 

class ActorCritic(nn.Module):
    def __init__(self, actor, critic):
        super().__init__()
        self.actor = actor
        self.critic = critic
    def forward(self, state):
        action_pred = self.actor(state)
        value_pred = self.critic(state)
        return action_pred, value_pred

Instanciar las redes de actores y críticos

Utilizaremos las redes definidas anteriormente para crear un actor y un crítico. A continuación, crearemos un agente, que incluirá al actor y al crítico. 

Antes de crear el agente, inicializa los parámetros de la red:

• Las dimensiones de la capa oculta, H, que es un parámetro configurable. El tamaño y el número de capas ocultas dependen de la complejidad del problema. Utilizaremos una capa oculta de dimensiones 64 X 64. 
• Características de entrada, N, donde N es el tamaño de la matriz de estados. La capa de entrada tiene dimensiones N X H. En el entorno CartPole, el estado es una matriz de 4 elementos. Entonces N es 4. 
• Características de salida de la red de actores, O, donde O es el número de acciones en el entorno. La capa de salida del actor tiene unas dimensiones H x O. El entorno de CartPole tiene 2 acciones. 
• Características de salida de la red crítica. Como la red crítica sólo predice el valor esperado (dado un estado de entrada), el número de características de salida es 1. 
• Abandono escolar como fracción.

El código siguiente muestra cómo declarar las redes de actores y críticos en función de la red troncal:

def create_agent(hidden_dimensions, dropout):
    INPUT_FEATURES = env_train.observation_space.shape[0]
    HIDDEN_DIMENSIONS = hidden_dimensions
    ACTOR_OUTPUT_FEATURES = env_train.action_space.n
    CRITIC_OUTPUT_FEATURES = 1
    DROPOUT = dropout
    actor = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, ACTOR_OUTPUT_FEATURES, DROPOUT)
    critic = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, CRITIC_OUTPUT_FEATURES, DROPOUT)
    agent = ActorCritic(actor, critic)
    return agent

Cálculo de los rendimientos

El entorno da una recompensa que va de cada paso al siguiente, en función de la acción del agente. La recompensa, R, se expresa como

El rendimiento se define como el valor acumulado de las recompensas futuras esperadas. Las recompensas de pasos temporales más lejanos en el futuro son menos valiosas que las recompensas inmediatas. Así, la rentabilidad se calcula comúnmente como la rentabilidad descontada, G, definida como:

En este tutorial (y en muchas otras referencias), rendimiento se refiere al rendimiento descontado. 

Para calcular el rendimiento:

• Empieza con las recompensas esperadas de todos los estados futuros.
• Multiplica cada recompensa futura por un exponente del factor de descuento, . Por ejemplo, la recompensa esperada tras 2 pasos temporales (desde el presente) se multiplica por 2. 
• Suma todas las recompensas futuras descontadas para calcular el rendimiento. 
• Normaliza el valor de la devolución. 

La función calculate_returns() realiza estos cálculos, como se muestra a continuación:

def calculate_returns(rewards, discount_factor):
    returns = []
    cumulative_reward = 0
    for r in reversed(rewards):
        cumulative_reward = r + cumulative_reward * discount_factor
        returns.insert(0, cumulative_reward)
    returns = torch.tensor(returns)
    # normalize the return
    returns = (returns - returns.mean()) / returns.std()
    return returns

Implementar la función de ventaja

La ventaja se calcula como la diferencia entre el valor predicho por el crítico y el rendimiento esperado de las acciones elegidas por el actor según la política. Para una acción determinada, la ventaja expresa el beneficio de realizar esa acción concreta frente a una acción arbitraria (media). 

En el documento PPO original (ecuación 10), la ventaja, mirando hacia adelante hasta el paso temporal T se expresa como:

Al codificar el algoritmo, la restricción de mirar hacia delante hasta un número determinado de pasos de tiempo se aplica mediante el tamaño del lote. Así pues, la ecuación anterior puede simplificarse como la diferencia entre el valor y los rendimientos esperados. Los rendimientos esperados se cuantifican en la función de valor estado-acción, Q. 

Así pues, la fórmula simplificada que figura a continuación expresa la ventaja de elegir: 

• una acción concreta 
• en un estado determinado 
• con una política determinada 
• en un determinado paso temporal 

Esto se expresa como 

OpenAI también utiliza esta fórmula para aplicar la RL. La función calculate_advantages() que se muestra a continuación calcula la ventaja:

def calculate_advantages(returns, values):
    advantages = returns - values
    # Normalize the advantage
    advantages = (advantages - advantages.mean()) / advantages.std()
    return advantages

Pérdida sustitutiva y mecanismo de recorte

La pérdida de la póliza sería la pérdida estándar del gradiente de la póliza, sin técnicas especiales como la PPO. La pérdida de gradiente de la política estándar se calcula como el producto de:

• Las probabilidades de acción política 
• La función de ventaja, que se calcula como la diferencia entre:
• La política de devolución 
• El valor esperado

La pérdida de gradiente de la política estándar no puede hacer correcciones por cambios bruscos de política. La pérdida sustitutiva modifica la pérdida estándar para restringir la cantidad que puede cambiar la política en cada iteración. Es el mínimo de dos cantidades:

• El producto de:
• La ratio política. Esta proporción expresa la diferencia entre las probabilidades de acción antiguas y las nuevas.  
• La función de ventaja 
• El producto de:
• El valor fijado de la relación de la política. Esta relación se recorta de forma que la política actualizada esté dentro de un determinado porcentaje de la política antigua. 
• La función de ventaja 

Para el proceso de optimización, la pérdida sustitutiva se utiliza como sustituto de la pérdida real. 

El mecanismo de recorte

La ratio de la política, Res la diferencia entre la política nueva y la antigua, y viene dada por el cociente de las probabilidades logarítmicas de la política con los parámetros nuevos y antiguos:

La ratio de la política recortada, R'se limita de modo que

Dada la ventaja, Atcomo se ha indicado en el apartado anterior, y el coeficiente de la política, como se ha indicado anteriormente, la pérdida sustitutiva se calcula como:

El código siguiente muestra cómo aplicar el mecanismo de recorte y la pérdida sustitutiva. 

def calculate_surrogate_loss(
        actions_log_probability_old,
        actions_log_probability_new,
        epsilon,
        advantages):
    advantages = advantages.detach()
    policy_ratio = (
            actions_log_probability_new - actions_log_probability_old
            ).exp()
    surrogate_loss_1 = policy_ratio * advantages
    surrogate_loss_2 = torch.clamp(
            policy_ratio, min=1.0-epsilon, max=1.0+epsilon
            ) * advantages
    surrogate_loss = torch.min(surrogate_loss_1, surrogate_loss_2)
    return surrogate_loss

3. Formación del Agente

Ahora, vamos a entrenar al agente.

Cálculo de la pérdida de póliza y de valor 

Ahora estamos preparados para calcular las pérdidas de la póliza y del valor: 

• La pérdida de la póliza es la suma de la pérdida sustitutiva y la prima de entropía. 
• Lapérdida de valorse basa en la diferencia entre el valor previsto por el crítico y los rendimientos (recompensa acumulada) generados por la póliza. El cálculo de la pérdida de valor utiliza la función de Pérdida Suave L1. Esto ayuda a suavizar la función de pérdida y la hace menos sensible a los valores atípicos.

Ambas pérdidas, tal como se han calculado anteriormente, son tensores. El descenso gradual se basa en valores escalares. Para obtener un único valor escalar que represente la pérdida, utiliza la función .sum() para sumar los elementos del tensor. La siguiente función muestra cómo hacerlo: 

def calculate_losses(
        surrogate_loss, entropy, entropy_coefficient, returns, value_pred):
    entropy_bonus = entropy_coefficient * entropy
    policy_loss = -(surrogate_loss + entropy_bonus).sum()
    value_loss = f.smooth_l1_loss(returns, value_pred).sum()
    return policy_loss, value_loss

Definir el bucle de entrenamiento

Antes de iniciar el proceso de entrenamiento, crea un conjunto de buffers como matrices vacías. El algoritmo de entrenamiento utilizará estos búferes para almacenar información sobre las acciones del agente, los estados del entorno y las recompensas en cada paso temporal. La siguiente función inicializa estos búferes: 

def init_training():
    states = []
    actions = []
    actions_log_probability = []
    values = []
    rewards = []
    done = False
    episode_reward = 0
    return states, actions, actions_log_probability, values, rewards, done, episode_reward

Cada iteración de entrenamiento ejecuta el agente con los parámetros de la política para esa iteración. El agente interactúa con el entorno en pasos de tiempo en un bucle hasta que alcanza una condición terminal. 

Después de cada paso temporal, la acción, la recompensa y el valor del agente se añaden a los búferes respectivos. Cuando termina el episodio, la función devuelve el conjunto actualizado de buffers, que resumen los resultados del episodio. 

Antes de ejecutar el bucle de entrenamiento:

• Pon el modelo en modo entrenamiento utilizando agent.train(). 
• Restablece el entorno a un estado aleatorio utilizando env.reset(). Este es el estado inicial para esta iteración de entrenamiento. 

Los pasos siguientes explican lo que ocurre en cada paso temporal del bucle de entrenamiento: 

• Pasa el estado al agente. 
• Vuelve el agente:
• La acción prevista dado el estado, en función de la política (actor). Pasa este tensor de acciones predichas por la función softmax para obtener el conjunto de probabilidades de acción.  
• El valor previsto del estado, basado en el crítico.
• El agente selecciona la acción a realizar:
• Utiliza las probabilidades de acción para estimar la distribución de probabilidad. 
• Selecciona aleatoriamente una acción escogiendo una muestra de esta distribución. La función dist.sample() lo hace. 
• Utiliza la función env.step() para pasar esta acción al entorno y simular la respuesta del entorno para este paso de tiempo. En función de la acción del agente, el entorno genera:
• El nuevo Estado
• La recompensa
• El valor booleano de retorno done (indica si el entorno ha alcanzado un estado terminal)
• Añade a los búferes respectivos los valores de la acción del agente, las recompensas, los valores predichos y el nuevo estado. 

El episodio de entrenamiento termina cuando la función env.step() devuelve true para el valor booleano de retorno de done. 

Una vez finalizado el episodio, utiliza los valores acumulados de cada paso temporal para calcular los rendimientos acumulados de este episodio sumando las recompensas de cada paso temporal. Para ello utilizamos la función calculate_returns() descrita anteriormente. Las entradas de esta función son el factor de descuento y el búfer que contiene las recompensas de cada paso temporal. Utilizamos estos rendimientos y los valores acumulados de cada paso temporal para calcular las ventajas mediante la función calculate_advantages(). 

La siguiente función de Python muestra cómo llevar a cabo estos pasos:

def forward_pass(env, agent, optimizer, discount_factor):
    states, actions, actions_log_probability, values, rewards, done, episode_reward = init_training()
    state = env.reset()
    agent.train()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        states.append(state)
        action_pred, value_pred = agent(state)
        action_prob = f.softmax(action_pred, dim=-1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)
        state, reward, done, _ = env.step(action.item())
        actions.append(action)
        actions_log_probability.append(log_prob_action)
        values.append(value_pred)
        rewards.append(reward)
        episode_reward += reward
    states = torch.cat(states)
    actions = torch.cat(actions)
    actions_log_probability = torch.cat(actions_log_probability)
    values = torch.cat(values).squeeze(-1)
    returns = calculate_returns(rewards, discount_factor)
    advantages = calculate_advantages(returns, values)
    return episode_reward, states, actions, actions_log_probability, advantages, returns

Actualizar los parámetros del modelo

Cada iteración de entrenamiento ejecuta el modelo a través de un episodio completo que consta de muchos pasos temporales (hasta que alcanza una condición terminal). En cada paso temporal, almacenamos los parámetros de la política, la acción del agente, los rendimientos y las ventajas. Después de cada iteración, actualizamos el modelo basándonos en el rendimiento de la política en todos los pasos temporales de esa iteración. 

El número máximo de pasos de tiempo en el entorno CartPole es 500. En entornos más complejos, hay más pasos temporales, incluso millones. En tales casos, el conjunto de datos de los resultados del entrenamiento debe dividirse en lotes. El número de pasos de tiempo de cada lote se denomina tamaño del lote de optimización. 

Así, los pasos para actualizar los parámetros del modelo son:

• Divide el conjunto de datos de los resultados del entrenamiento en lotes. 
• Para cada lote:
• Obtén la acción del agente y el valor previsto para cada estado.
• Utiliza estas acciones previstas para estimar la nueva distribución de probabilidad de acción. 
• Utiliza esta distribución para calcular la entropía. 
• Utiliza esta distribución para obtener la probabilidad logarítmica de las acciones en el conjunto de datos de resultados del entrenamiento. Es el nuevo conjunto de probabilidades logarítmicas de las acciones del conjunto de datos de resultados del entrenamiento. El antiguo conjunto de probabilidades logarítmicas de estas mismas acciones se calculó en el bucle de entrenamiento explicado en la sección anterior. 
• Calcula la pérdida sustitutiva utilizando las distribuciones de probabilidad antigua y nueva de las acciones. 
• Calcula la pérdida política y la pérdida de valor utilizando la pérdida sustitutiva, la entropía y las ventajas. 
• Ejecuta .backward() por separado en la póliza y valora las pérdidas. Así se actualizan los gradientes de las funciones de pérdida. 
• Ejecuta .step() en el optimizador para actualizar los parámetros de la política. En este caso, utilizamos el optimizador Adam para equilibrar velocidad y robustez. 
• Acumula la póliza y valora las pérdidas. 
• Repite el paso hacia atrás (las operaciones anteriores) en cada lote unas cuantas veces, en función del valor del parámetro PPO_STEPS. Repetir el paso hacia atrás en cada lote es eficiente desde el punto de vista informático, porque aumenta efectivamente el tamaño del conjunto de datos de entrenamiento sin tener que ejecutar pases hacia delante adicionales. El número de pasos del entorno en cada alternancia entre muestreo y optimización se denomina tamaño del lote de iteración. 
• Devuelve la pérdida media de la póliza y la pérdida de valor.

El código siguiente implementa estos pasos:

def update_policy(
        agent,
        states,
        actions,
        actions_log_probability_old,
        advantages,
        returns,
        optimizer,
        ppo_steps,
        epsilon,
        entropy_coefficient):
    BATCH_SIZE = 128
    total_policy_loss = 0
    total_value_loss = 0
    actions_log_probability_old = actions_log_probability_old.detach()
    actions = actions.detach()
    training_results_dataset = TensorDataset(
            states,
            actions,
            actions_log_probability_old,
            advantages,
            returns)
    batch_dataset = DataLoader(
            training_results_dataset,
            batch_size=BATCH_SIZE,
            shuffle=False)
    for _ in range(ppo_steps):
        for batch_idx, (states, actions, actions_log_probability_old, advantages, returns) in enumerate(batch_dataset):
            # get new log prob of actions for all input states
            action_pred, value_pred = agent(states)
            value_pred = value_pred.squeeze(-1)
            action_prob = f.softmax(action_pred, dim=-1)
            probability_distribution_new = distributions.Categorical(
                    action_prob)
            entropy = probability_distribution_new.entropy()
            # estimate new log probabilities using old actions
            actions_log_probability_new = probability_distribution_new.log_prob(actions)
            surrogate_loss = calculate_surrogate_loss(
                    actions_log_probability_old,
                    actions_log_probability_new,
                    epsilon,
                    advantages)
            policy_loss, value_loss = calculate_losses(
                    surrogate_loss,
                    entropy,
                    entropy_coefficient,
                    returns,
                    value_pred)
            optimizer.zero_grad()
            policy_loss.backward()
            value_loss.backward()
            optimizer.step()
            total_policy_loss += policy_loss.item()
            total_value_loss += value_loss.item()
    return total_policy_loss / ppo_steps, total_value_loss / ppo_steps

4. Ejecutar el Agente PPO 

Por último, pongamos en marcha al agente PPO.

Evaluar el rendimiento 

Para evaluar el rendimiento del agente, crea un nuevo entorno y calcula las recompensas acumuladas al ejecutar el agente en este nuevo entorno. Tienes que poner al agente en modo evaluación utilizando la función .eval(). Los pasos son los mismos que para el bucle de entrenamiento. El fragmento de código siguiente implementa la función de evaluación: 

def evaluate(env, agent):
    agent.eval()
    rewards = []
    done = False
    episode_reward = 0
    state = env.reset()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        with torch.no_grad():
            action_pred, _ = agent(state)
            action_prob = f.softmax(action_pred, dim=-1)
        action = torch.argmax(action_prob, dim=-1)
        state, reward, done, _ = env.step(action.item())
        episode_reward += reward
    return episode_reward

Visualizar los resultados del entrenamiento

Utilizaremos la biblioteca Matplotlib para visualizar el progreso del proceso de entrenamiento. La función siguiente muestra cómo trazar las recompensas de los bucles de entrenamiento y de prueba:

def plot_train_rewards(train_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(train_rewards, label='Training Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Training Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(train_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

def plot_test_rewards(test_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(test_rewards, label='Testing Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Testing Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(test_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

En los gráficos de ejemplo que aparecen a continuación, mostramos las recompensas de entrenamiento y de prueba, obtenidas al aplicar la política en los entornos de entrenamiento y de prueba, respectivamente. Ten en cuenta que la forma de estos gráficos será diferente cada vez que ejecutes el código. Esto se debe a la aleatoriedad inherente al proceso de entrenamiento. 

Recompensas de entrenamiento (obtenidas aplicando la política en el entorno de entrenamiento). Imagen del autor.

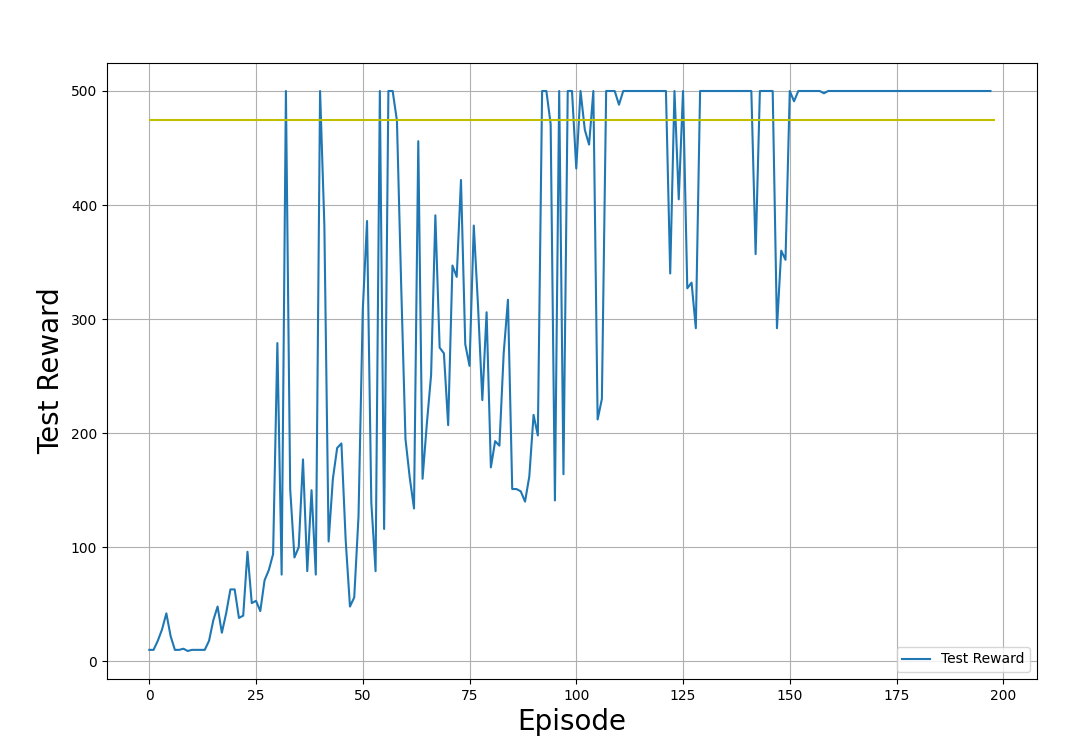
Recompensas de prueba (obtenidas aplicando la política en el entorno de prueba). Imagen del autor. 

En los gráficos de salida mostrados arriba, observa el progreso del proceso de entrenamiento:

• La recompensa parte de valores bajos. A medida que avanza el entrenamiento, aumentan las recompensas. 
• Las recompensas fluctúan aleatoriamente mientras aumentan. Esto se debe a que el agente explora el espacio político. 
• El entrenamiento termina, y las recompensas de las pruebas se han estabilizado en torno al umbral (475) durante muchas iteraciones. 
• Las recompensas tienen un límite de 500. Son restricciones impuestas por el entorno (Gimnasio CartPole v1). 

Del mismo modo, puedes trazar el valor y las pérdidas de la póliza a través de las iteraciones:

def plot_losses(policy_losses, value_losses):
    plt.figure(figsize=(12, 8))
    plt.plot(value_losses, label='Value Losses')
    plt.plot(policy_losses, label='Policy Losses')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Loss', fontsize=20)
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

El gráfico de ejemplo de abajo muestra las pérdidas seguidas a lo largo de los episodios de entrenamiento:

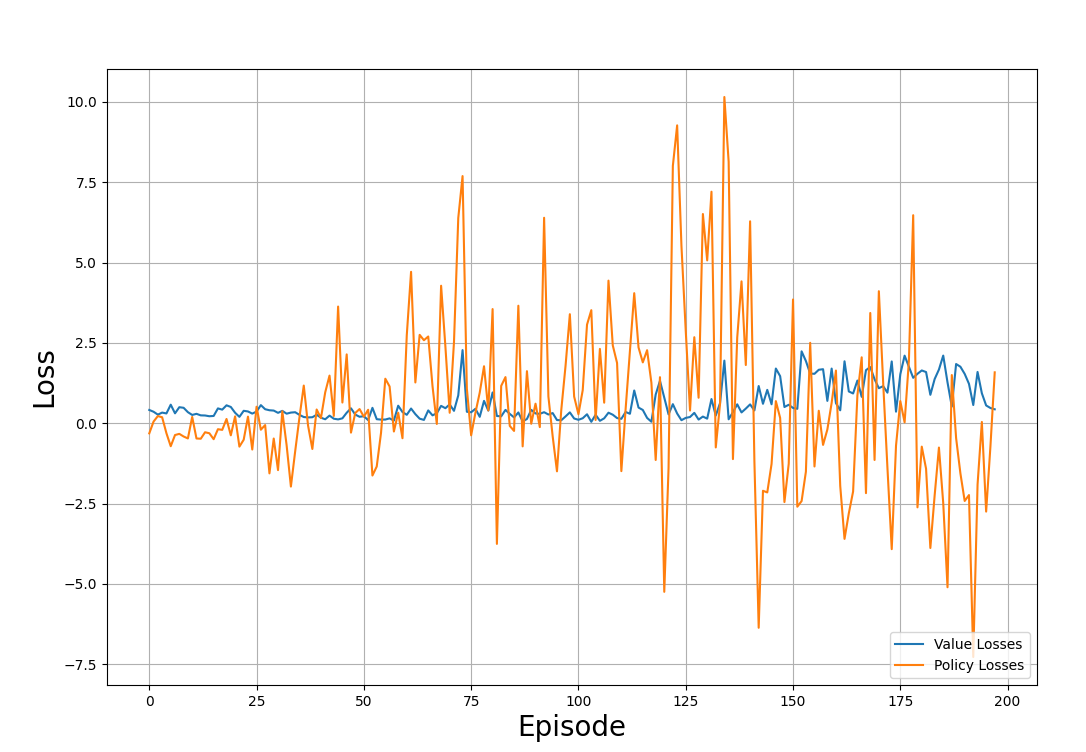
Valor y pérdidas de pólizas a través del proceso de formación. Imagen del autor

Observa la trama y date cuenta:

• Las pérdidas parecen estar distribuidas aleatoriamente y no siguen ningún patrón. 
• Esto es típico del entrenamiento RL, en el que el objetivo no es minimizar la pérdida, sino maximizar las recompensas. 

Ejecuta el algoritmo PPO

Ahora tienes todos los componentes para formar al agente mediante PPO. Para ponerlo todo junto, necesitas

• Declara hiperparámetros como el factor de descuento, el tamaño del lote, la tasa de aprendizaje, etc. 
• Instala buffers como matrices nulas para almacenar las recompensas y pérdidas de cada iteración. 
• Crea una instancia de agente utilizando la función create_agent().
• Ejecuta iterativamente pasadas hacia delante y hacia atrás utilizando las funciones forward_pass() y update_policy(). 
• Comprueba el funcionamiento de la política utilizando la función evaluate(). 
• Añade la política, las pérdidas de valor y las recompensas de las funciones de entrenamiento y evaluación a los búferes respectivos. 
• Calcula la media de las recompensas y pérdidas de los últimos pasos temporales. El ejemplo siguiente promedia las recompensas y las pérdidas de los últimos 40 pasos temporales. 
• Imprime los resultados de la evaluación cada pocos pasos. El ejemplo siguiente imprime cada 10 pasos. 
• Finaliza el proceso cuando la recompensa media supere un determinado umbral. 

El código siguiente muestra cómo declarar una función que haga esto en Python:

def run_ppo():
    MAX_EPISODES = 500
    DISCOUNT_FACTOR = 0.99
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    PPO_STEPS = 8
    N_TRIALS = 100
    EPSILON = 0.2
    ENTROPY_COEFFICIENT = 0.01
    HIDDEN_DIMENSIONS = 64
    DROPOUT = 0.2
    LEARNING_RATE = 0.001
    train_rewards = []
    test_rewards = []
    policy_losses = []
    value_losses = []
    agent = create_agent(HIDDEN_DIMENSIONS, DROPOUT)
    optimizer = optim.Adam(agent.parameters(), lr=LEARNING_RATE)
    for episode in range(1, MAX_EPISODES+1):
        train_reward, states, actions, actions_log_probability, advantages, returns = forward_pass(
                env_train,
                agent,
                optimizer,
                DISCOUNT_FACTOR)
        policy_loss, value_loss = update_policy(
                agent,
                states,
                actions,
                actions_log_probability,
                advantages,
                returns,
                optimizer,
                PPO_STEPS,
                EPSILON,
                ENTROPY_COEFFICIENT)
        test_reward = evaluate(env_test, agent)
        policy_losses.append(policy_loss)
        value_losses.append(value_loss)
        train_rewards.append(train_reward)
        test_rewards.append(test_reward)
        mean_train_rewards = np.mean(train_rewards[-N_TRIALS:])
        mean_test_rewards = np.mean(test_rewards[-N_TRIALS:])
        mean_abs_policy_loss = np.mean(np.abs(policy_losses[-N_TRIALS:]))
        mean_abs_value_loss = np.mean(np.abs(value_losses[-N_TRIALS:]))
        if episode % PRINT_INTERVAL == 0:
            print(f'Episode: {episode:3} | \
                  Mean Train Rewards: {mean_train_rewards:3.1f} \
                  | Mean Test Rewards: {mean_test_rewards:3.1f} \
                  | Mean Abs Policy Loss: {mean_abs_policy_loss:2.2f} \
                  | Mean Abs Value Loss: {mean_abs_value_loss:2.2f}')
        if mean_test_rewards >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break
    plot_train_rewards(train_rewards, REWARD_THRESHOLD)
    plot_test_rewards(test_rewards, REWARD_THRESHOLD)
    plot_losses(policy_losses, value_losses)

Ejecuta el programa: 

run_ppo()

El resultado debe parecerse a la muestra de abajo: 

Episode:  10 | Mean Train Rewards: 22.3 | Mean Test Rewards: 30.4 | Mean Abs Policy Loss: 0.37 | Mean Abs Value Loss: 0.39 
Episode:  20 | Mean Train Rewards: 38.6 | Mean Test Rewards: 69.8 | Mean Abs Policy Loss: 0.46 | Mean Abs Value Loss: 0.37 
.
.
.
Episode: 100 | Mean Train Rewards: 289.5 | Mean Test Rewards: 427.3 | Mean Abs Policy Loss: 1.73 | Mean Abs Value Loss: 0.21 
Episode: 110 | Mean Train Rewards: 357.7 | Mean Test Rewards: 461.4 | Mean Abs Policy Loss: 1.86 | Mean Abs Value Loss: 0.22 
Reached reward threshold in 116 episodes

¡Puedes ver y ejecutar elprograma de trabajo en este cuaderno DataLab!

5. Ajuste y optimización de hiperparámetros

En el aprendizaje automático, los hiperparámetros controlan el proceso de entrenamiento. A continuación, explico algunos de los hiperparámetros importantes utilizados en la OPP: 

• Ritmo de aprendizaje: La tasa de aprendizaje decide cuánto pueden variar los parámetros de la política en cada iteración. En el descenso por gradiente estocástico, la cantidad en que se actualizan los parámetros de la política en cada iteración se decide por el producto de la tasa de aprendizaje y el gradiente. 
• Parámetro de recorte: También se denomina épsilon, ε. Decide hasta qué punto se recorta el ratio de la política. Se permite que la relación entre las pólizas nueva y antigua varíe en el intervalo [1-ε, 1+ε]. Cuando está fuera de este intervalo, se recorta artificialmente para que quede dentro del intervalo. 
• Tamaño del lote: Se refiere al número de pasos a considerar para cada actualización del gradiente. En la PPO, el tamaño del lote es el número de pasos temporales necesarios para aplicar la política y calcular la pérdida sustitutiva para actualizar los parámetros de la política. En este artículo, hemos utilizado un tamaño de lote de 64. 
• Pasos de iteración: Es el número de veces que se reutiliza cada lote para ejecutar la pasada hacia atrás. El código de este artículo se refiere a esto como PPO_STEPS. En entornos complejos, ejecutar el pase hacia delante muchas veces es costoso desde el punto de vista informático. Una alternativa más eficaz es volver a ejecutar cada lote varias veces. Normalmente se recomienda utilizar un valor entre 5 y 10. 
• Factor de descuento: También se denomina gamma, γ. Expresa hasta qué punto las recompensas inmediatas son más valiosas que las recompensas futuras. Esto es similar al concepto de tipos de interés en el cálculo del valor temporal del dinero. Cuando está más cerca de 0, significa que las recompensas futuras son menos valiosas y que el agente debe dar prioridad a las recompensas inmediatas. Cuando está más cerca de 1, significa que las recompensas futuras son importantes .
• Coeficiente de entropía: El coeficiente de entropía decide la prima de entropía, que se calcula como el producto del coeficiente de entropía y la entropía de la distribución. La función de la prima de entropía es introducir más aleatoriedad en la política. Esto anima al agente a explorar el espacio político. Sin embargo, el entrenamiento no consigue converger a una política óptima cuando esta aleatoriedad es demasiado alta. 
• Criterios de éxito de la formación: Tienes que establecer los criterios para decidir cuándo la formación ha tenido éxito. Una forma habitual de hacerlo es poner como condición que la recompensa media de los últimos N ensayos (episodios) esté por encima de un determinado umbral. En el código de ejemplo anterior, esto se expresa con la variable N_TRIALS. Cuando se ajusta a un valor más alto, el entrenamiento lleva más tiempo porque la política tiene que alcanzar el umbral de recompensa en más episodios. También da lugar a una política más robusta, aunque es computacionalmente más cara. Ten en cuenta que la PPO es una política estocástica, y habrá episodios en los que el agente no cruce el umbral. Por tanto, si el valor de N_TRIALS es demasiado alto, puede que tu entrenamiento no termine.

Estrategias para optimizar el rendimiento de la OPP

Optimizar el rendimiento de los algoritmos PPO de entrenamiento implica ensayo y error y experimentar con distintos valores de hiperparámetros. Sin embargo, existen algunas directrices generales: 

• Factor de descuento: Cuando las recompensas a largo plazo son importantes, como en el entorno CartPole, donde el polo debe permanecer estable a lo largo del tiempo, empieza con un valor gamma moderado, como 0,99. 
• Bonificación por entropía: En entornos complejos, el agente debe explorar el espacio de acción para encontrar la política óptima. La bonificación de entropía fomenta la exploración. La prima de entropía se añade a la pérdida de sustituto. Comprueba la magnitud de la pérdida sustitutiva y la entropía de la distribución antes de decidir el coeficiente de entropía. En este artículo, hemos utilizado un coeficiente de entropía de 0,01.
• Parámetro de recorte: El parámetro de recorte decide lo diferente que puede ser la política actualizada de la política actual. Un valor grande del parámetro de recorte favorece una mejor exploración del entorno, pero corre el riesgo de desestabilizar el entrenamiento. Quieres un parámetro de recorte que permita una exploración gradual, evitando al mismo tiempo actualizaciones desestabilizadoras. En este artículo, hemos utilizado un parámetro de recorte de 0,2.
• Ritmo de aprendizaje: Cuando la tasa de aprendizaje es demasiado alta, la política se actualiza en grandes pasos, y cada iteración y el proceso de entrenamiento pueden volverse inestables. Cuando es demasiado bajo, el entrenamiento dura demasiado.  Este tutorial utilizó una tasa de aprendizaje de 0,001, que funciona bien para el entorno. En muchos casos, se recomienda utilizar una tasa de aprendizaje de 1e-5. 

Retos y buenas prácticas en la OPP

Tras explicar los conceptos de la PPO y los detalles de su implantación, vamos a hablar de los retos y las mejores prácticas. 

Desafíos comunes en la formación de PPO

Aunque la OPP se utiliza ampliamente, debes ser consciente de los retos potenciales para resolver problemas del mundo real utilizando esta técnica con éxito. Algunos de estos retos son:

• Convergencia lenta: En entornos complejos, la OPP puede ser ineficiente desde el punto de vista muestral y necesita muchas interacciones con el entorno para converger en la política óptima. Esto hace que su formación sea lenta y costosa. 
• Sensibilidad a los hiperparámetros: La OPP se basa en la exploración eficaz del espacio político. La estabilidad del proceso de entrenamiento y la velocidad de convergencia son sensibles a los valores de los hiperparámetros. A menudo, los valores óptimos de estos hiperparámetros sólo pueden determinarse por ensayo y error. 
• Sobreajuste:  Los entornos RL suelen inicializarse con parámetros aleatorios. El entrenamiento PPO se basa en encontrar la política óptima en función del entorno del agente. A veces, el proceso de entrenamiento converge a un conjunto de parámetros óptimos para un entorno concreto, pero no para cualquier entorno aleatorio. Esto se suele solucionar teniendo muchas iteraciones, cada una con un entorno de entrenamiento aleatorio diferente. 
• Entornos dinámicos: Los entornos de RL sencillos, como el de CartPole, son estáticos: las reglas son las mismas a lo largo del tiempo. Muchos otros entornos, como un robot que aprende a caminar sobre una superficie móvil inestable, son dinámicos: las reglas del entorno cambian con el tiempo. Para funcionar bien en esos entornos, la OPP a menudo necesita un ajuste adicional. 
• Exploración frente a explotación: El mecanismo de recorte de la OPP garantiza que las actualizaciones de las políticas estén dentro de una región de confianza. Sin embargo, también impide que el agente explore el espacio de acción. Esto puede llevar a la convergencia a óptimos locales, sobre todo en entornos complejos. Por otra parte, permitir que el agente explore demasiado puede impedirle converger hacia cualquier política óptima. 

Buenas prácticas para la formación de modelos PPO

Para obtener buenos resultados utilizando PPO, recomiendo algunas prácticas recomendadas, como:

• Normaliza las características de entrada: Normalizar los valores de rendimientos y ventajas reduce la variabilidad de los datos y conduce a actualizaciones estables del gradiente. Normalizar los datos lleva todos los valores a un rango numérico coherente. Ayuda a reducir el efecto de los valores atípicos y extremos, que de otro modo podrían distorsionar las actualizaciones del gradiente y ralentizar la convergencia. 
• Utiliza lotes de tamaño adecuado: Los lotes pequeños permiten actualizaciones y entrenamientos más rápidos, pero pueden conducir a la convergencia a óptimos locales y a la inestabilidad en el proceso de entrenamiento. Los lotes de mayor tamaño permiten al agente aprender políticas sólidas, lo que conduce a un proceso de entrenamiento estable. Sin embargo, los tamaños de lote demasiado grandes tampoco son óptimos. Además de aumentar los costes computacionales, hacen que las actualizaciones de las políticas respondan menos a la función de valor, porque las actualizaciones del gradiente se basan en medias estimadas sobre grandes lotes. Además, puede llevar a sobreajustar las actualizaciones a ese lote concreto. 
• Pasos de iteración: En general, es aconsejable reutilizar cada lote durante 5-10 iteraciones. Esto hace que el proceso de formación sea más eficaz. Reutilizar el mismo lote demasiadas veces conduce a un sobreajuste. El código se refiere a este hiperparámetro como PPO_STEPS. 
• Realiza una evaluación periódica: Para detectar el sobreajuste, es esencial controlar periódicamente la eficacia de la política. Si la política resulta ineficaz en determinadas situaciones, puede que sea necesario seguir formándola o afinarla. 
• Ajusta los hiperparámetros: Como ya se ha explicado, el entrenamiento de la PPO es sensible a los valores de los hiperparámetros. Experimenta con varios valores de hiperparámetros para determinar el conjunto de valores adecuado para tu problema concreto. 
• Red troncal compartida: Como se ilustra en este artículo, utilizar una red troncal compartida evita desequilibrios entre las redes de actores y críticos. Compartir una red troncal entre el actor y el crítico ayuda a la extracción de características compartidas y a una comprensión común del entorno. Esto hace que el proceso de aprendizaje sea más eficaz y estable. También ayuda a reducir el espacio computacional y la complejidad temporal del algoritmo. 
• Número y tamaño de las capas ocultas: Aumenta el número de capas ocultas y dimensiones para entornos más complejos. Los problemas más sencillos, como CartPole, pueden resolverse con una sola capa oculta. La capa oculta utilizada en este artículo tiene 64 dimensiones. Hacer la red mucho más grande de lo necesario es un derroche computacional y puede hacerla inestable. 
• Parada anticipada: Detener el entrenamiento cuando se cumplen las métricas de evaluación ayuda a prevenir el sobreentrenamiento y evita el despilfarro de recursos. Una métrica de evaluación habitual es cuando el agente supera el umbral de recompensas en los últimos N eventos. 

Conclusión

En este artículo hablamos de la OPP como forma de resolver los problemas de RL. A continuación, detallamos los pasos para poner en práctica la OPP utilizando PyTorch. Por último, presentamos algunos consejos de rendimiento y buenas prácticas para la PPO. 

La mejor forma de aprender es aplicar tú mismo el código. También puedes modificar el código para que funcione con otros entornos de control clásicos en Gym. Para aprender a implementar agentes de RL utilizando Python y Gymnasium de OpenAI, ¡sigue el curso Aprendizaje por Refuerzo con Gymnasium en Python!