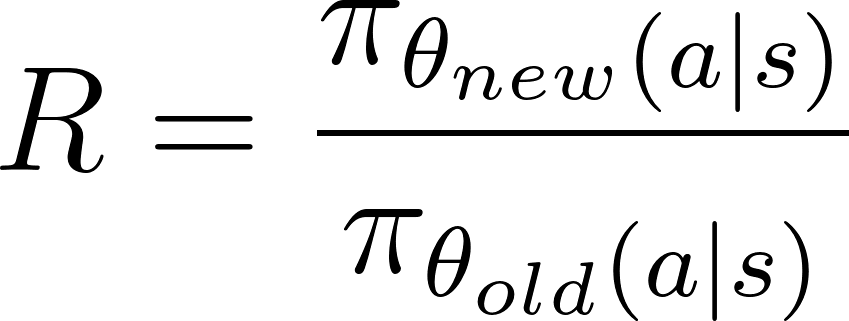Proximale Optimierung von Richtlinien mit PyTorch und Gymnasium

1. Einrichten der Umgebung 

Bevor wir PPO implementieren, müssen wir die erforderlichen Softwarebibliotheken installieren und eine geeignete Umgebung für die Anwendung der Richtlinie auswählen. 

Installation von PyTorch und den erforderlichen Bibliotheken 

Wir müssen die folgende Software installieren: 

• PyTorch und andere Softwarebibliotheken wie numpy (für mathematische und statistische Funktionen) und matplotlib (zum Plotten von Diagrammen).
• Das Open-Source-Softwarepaket Gym von OpenAI, eine Python-Bibliothek, die verschiedene Umgebungen und Spiele simuliert, die mit Reinforcement Learning gelöst werden können. Du kannst die Gym-API nutzen, um deinen Algorithmus mit der Umgebung interagieren zu lassen. Da sich die Funktionalität von gym durch den Upgrade-Prozess manchmal ändert, frieren wir in diesem Beispiel die Version auf 0.25.2.

Um auf einem Server oder einem lokalen Rechner zu installieren, führe aus: 

$ pip install torch numpy matplotlib gym==0.25.2

Für die Installation mit einem Notebook wie Google Colaboder DataLab verwendest du: 

!pip install torch numpy matplotlib gym==0.25.2

Erstelle die CartPole Umgebung(en)

Verwende OpenAI Gym, um zwei Instanzen der CartPole-Umgebung zu erstellen (eine zum Trainieren und eine zum Testen):

env_train = gym.make('CartPole-v1')
env_test = gym.make('CartPole-v1')

2. PPO in PyTorch implementieren

Jetzt wollen wir PPO mit PyTorch implementieren.

Definition des Politiknetzwerks

Wie bereits erläutert, wird das PPO als akteurskritisches Modell umgesetzt. Der Akteur setzt die Politik um, und der Kritiker sagt ihren geschätzten Wert voraus. Neuronale Netze von Akteuren und Kritikern nehmen den gleichen Input - den Zustand in jedem Zeitschritt. So können sich das Akteurs- und das Kritikermodell ein gemeinsames neuronales Netz teilen, das als Backbone-Architektur bezeichnet wird. Der Akteur und der Kritiker können die Backbone-Architektur mit zusätzlichen Schichten erweitern. 

Definiere das Backbone-Netzwerk

Die folgenden Schritte beschreiben das Backbone-Netzwerk:

• Implementiere ein Netzwerk mit 3 Schichten - einer Eingabe-, einer versteckten und einer Ausgabeschicht. 
• Nach der Eingabe- und der versteckten Schicht verwenden wir eine Aktivierungsfunktion. In diesem Lernprogramm wählen wir ReLU, weil es rechenintensiv ist. 
• Um ein robustes Netz zu erhalten, setzen wir außerdem eine Dropout-Funktion nach der Eingabe- und der versteckten Schicht ein. Die Dropout-Funktion setzt einige Neuronen nach dem Zufallsprinzip auf Null. Dies verringert die Abhängigkeit von bestimmten Neuronen und verhindert eine Überanpassung, wodurch das Netz robuster wird. 

Der folgende Code implementiert das Backbone:

class BackboneNetwork(nn.Module):
    def __init__(self, in_features, hidden_dimensions, out_features, dropout):
        super().__init__()
        self.layer1 = nn.Linear(in_features, hidden_dimensions)
        self.layer2 = nn.Linear(hidden_dimensions, hidden_dimensions)
        self.layer3 = nn.Linear(hidden_dimensions, out_features)
        self.dropout = nn.Dropout(dropout)
    def forward(self, x):
        x = self.layer1(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer2(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer3(x)
        return x

Definiere das Akteur-Kritik-Netzwerk

Nun können wir dieses Netzwerk nutzen, um die Akteur-Kritik-Klasse ActorCritic zu definieren. Der Akteur modelliert die Politik und sagt die Handlung voraus. Der Kritiker modelliert die Wertfunktion und sagt den Wert voraus. Sie nehmen beide den Zustand als Input. 

class ActorCritic(nn.Module):
    def __init__(self, actor, critic):
        super().__init__()
        self.actor = actor
        self.critic = critic
    def forward(self, state):
        action_pred = self.actor(state)
        value_pred = self.critic(state)
        return action_pred, value_pred

Instanziere die Netzwerke der Akteure und Kritiker

Wir verwenden die oben definierten Netzwerke, um einen Schauspieler und einen Kritiker zu erstellen. Dann erstellen wir einen Agenten, der den Schauspieler und den Kritiker enthält. 

Bevor du den Agenten erstellst, musst du die Parameter des Netzwerks initialisieren:

• Die Größe der versteckten Schicht, H, ist ein konfigurierbarer Parameter. Die Größe und Anzahl der verborgenen Schichten hängt von der Komplexität des Problems ab. Wir verwenden eine versteckte Schicht mit 64 x 64 Dimensionen. 
• Eingabe von Merkmalen, N, wobei N die Größe des Zustandsfeldes ist. Die Eingabeschicht hat N X H Dimensionen. In der CartPole Umgebung ist der Zustand ein Array mit 4 Elementen. N ist also 4. 
• Ausgangsmerkmale des Akteursnetzwerks, O, wobei O die Anzahl der Aktionen in der Umgebung ist. Die Ausgangsschicht des Akteurs hat die Dimensionen H x O. Die CartPole Umgebung hat 2 Aktionen. 
• Ausgangsmerkmale des kritischen Netzwerks. Da das kritische Netz nur den erwarteten Wert (bei einem Eingangszustand) vorhersagt, ist die Anzahl der Ausgangsmerkmale 1. 
• Schulabbruch als Anteil.

Der folgende Code zeigt, wie du die Akteurs- und Kritiker-Netzwerke auf der Grundlage des Backbone-Netzwerks deklarierst:

def create_agent(hidden_dimensions, dropout):
    INPUT_FEATURES = env_train.observation_space.shape[0]
    HIDDEN_DIMENSIONS = hidden_dimensions
    ACTOR_OUTPUT_FEATURES = env_train.action_space.n
    CRITIC_OUTPUT_FEATURES = 1
    DROPOUT = dropout
    actor = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, ACTOR_OUTPUT_FEATURES, DROPOUT)
    critic = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, CRITIC_OUTPUT_FEATURES, DROPOUT)
    agent = ActorCritic(actor, critic)
    return agent

Die Berechnung der Rendite

Die Umgebung gibt eine Belohnung, die von jedem Schritt zum nächsten geht, abhängig von der Aktion des Agenten. Die Belohnung, R, wird wie folgt ausgedrückt:

Die Rendite ist definiert als der kumulierte Wert der erwarteten zukünftigen Erträge. Belohnungen aus Zeitschritten, die weiter in der Zukunft liegen, sind weniger wertvoll als unmittelbare Belohnungen. Daher wird die Rendite in der Regel als diskontierte Rendite G berechnet, die wie folgt definiert ist:

In diesem Tutorial (und in vielen anderen Referenzen) bezieht sich der Begriff Rendite auf die abgezinste Rendite. 

So berechnest du die Rendite:

• Beginne mit den erwarteten Belohnungen aus allen zukünftigen Zuständen.
• Multipliziere jede zukünftige Belohnung mit einem Exponenten des Diskontierungsfaktors, . Zum Beispiel wird die erwartete Belohnung nach 2 Zeitschritten (von jetzt an) mit 2 multipliziert. 
• Addiere alle abgezinsten zukünftigen Erträge, um die Rendite zu berechnen. 
• Normalisiere den Wert der Rückgabe. 

Die Funktion calculate_returns() führt diese Berechnungen durch, wie unten gezeigt:

def calculate_returns(rewards, discount_factor):
    returns = []
    cumulative_reward = 0
    for r in reversed(rewards):
        cumulative_reward = r + cumulative_reward * discount_factor
        returns.insert(0, cumulative_reward)
    returns = torch.tensor(returns)
    # normalize the return
    returns = (returns - returns.mean()) / returns.std()
    return returns

Implementierung der Vorteilsfunktion

Der Vorteil errechnet sich aus der Differenz zwischen dem vom Kritiker vorhergesagten Wert und dem erwarteten Ertrag aus den Handlungen, die der Akteur gemäß der Strategie gewählt hat. Für eine bestimmte Handlung drückt der Vorteil den Nutzen aus, den diese spezifische Handlung gegenüber einer beliebigen (durchschnittlichen) Handlung hat. 

In dem ursprünglichen PPO-Papier (Gleichung 10) wird der Vorteil mit Blick auf den Zeitschritt T wie folgt ausgedrückt:

Bei der Codierung des Algorithmus wird die Bedingung, bis zu einer bestimmten Anzahl von Zeitschritten in die Zukunft zu blicken, durch die Stapelgröße erzwungen. Die obige Gleichung lässt sich also vereinfacht als die Differenz zwischen dem Wert und den erwarteten Erträgen darstellen. Die erwarteten Renditen werden in der State-Action-Value-Funktion, Q, quantifiziert. 

Die folgende vereinfachte Formel drückt also den Vorteil der Wahl aus: 

• eine bestimmte Aktion 
• in einem bestimmten Zustand 
• unter einer bestimmten Police 
• zu einem bestimmten Zeitschritt 

Dies wird ausgedrückt als: 

Auch OpenAI nutzt diese Formel , um RL zu implementieren. Dieunten abgebildete Funktion calculate_advantages() berechnet den Vorteil:

def calculate_advantages(returns, values):
    advantages = returns - values
    # Normalize the advantage
    advantages = (advantages - advantages.mean()) / advantages.std()
    return advantages

Ersatzverlust und Begrenzungsmechanismus

Der Versicherungsverlust wäre der normale Gradientenverlust ohne spezielle Techniken wie PPO. Der Standard-Gradientenverlust wird berechnet als das Produkt aus:

• Die Wahrscheinlichkeiten für politische Maßnahmen 
• Die Vorteilsfunktion, die sich aus der Differenz zwischen:
• Die Rückgabe der Police 
• Der erwartete Wert

Der Standard-Gradientenverlust kann keine Korrekturen für abrupte Änderungen der Politik vornehmen. Der Ersatzverlust modifiziert den Standardverlust, um den Betrag zu begrenzen, den die Police in jeder Iteration ändern kann. Es ist das Minimum von zwei Mengen:

• Das Produkt von:
• Die Politikquote. Dieses Verhältnis drückt den Unterschied zwischen der alten und der neuen Handlungswahrscheinlichkeit aus.  
• Die Vorteilsfunktion 
• Das Produkt von:
• Der geklemmte Wert der Politikquote. Dieses Verhältnis wird so beschnitten, dass die aktualisierte Police innerhalb eines bestimmten Prozentsatzes der alten Police liegt. 
• Die Vorteilsfunktion 

Für den Optimierungsprozess wird der Surrogatverlust als Ersatz für den tatsächlichen Verlust verwendet. 

Der Clipping-Mechanismus

Die Politikquote, Rist der Unterschied zwischen der neuen und der alten Politik und wird als Verhältnis der logarithmischen Wahrscheinlichkeiten der Politik unter den neuen und alten Parametern angegeben:

Das abgeschnittene Politikverhältnis, R'ist so begrenzt, dass:

Wenn du den Vorteil hast, Atwie im vorangegangenen Abschnitt gezeigt, und der Politikquote, wie oben gezeigt, wird der Ersatzverlust wie folgt berechnet:

Der folgende Code zeigt, wie der Clipping-Mechanismus und der Surrogatverlust implementiert werden. 

def calculate_surrogate_loss(
        actions_log_probability_old,
        actions_log_probability_new,
        epsilon,
        advantages):
    advantages = advantages.detach()
    policy_ratio = (
            actions_log_probability_new - actions_log_probability_old
            ).exp()
    surrogate_loss_1 = policy_ratio * advantages
    surrogate_loss_2 = torch.clamp(
            policy_ratio, min=1.0-epsilon, max=1.0+epsilon
            ) * advantages
    surrogate_loss = torch.min(surrogate_loss_1, surrogate_loss_2)
    return surrogate_loss

3. Ausbildung des Agenten

Jetzt wollen wir den Agenten trainieren.

Berechnung von Police und Wertverlust 

Jetzt können wir die Verluste aus der Police und den Wert berechnen: 

• Der Versicherungsschaden ist die Summe aus dem Ersatzschaden und dem Entropie-Bonus. 
• Der Wertverlustbasiert auf der Differenz zwischen dem vom Kritiker vorhergesagten Wert und den durch die Police erzielten Erträgen (kumulative Belohnung). Für die Berechnung des Wertverlustes wird die Funktion Smooth L1 Loss verwendet. Dies hilft, die Verlustfunktion zu glätten und macht sie weniger empfindlich gegenüber Ausreißern.

Beide Verluste, die oben berechnet wurden, sind Tensoren. Der Gradientenabstieg basiert auf skalaren Werten. Um einen einzelnen skalaren Wert zu erhalten, der den Verlust darstellt, benutze die Funktion .sum(), um die Tensorelemente zu summieren. Die folgende Funktion zeigt, wie man das macht: 

def calculate_losses(
        surrogate_loss, entropy, entropy_coefficient, returns, value_pred):
    entropy_bonus = entropy_coefficient * entropy
    policy_loss = -(surrogate_loss + entropy_bonus).sum()
    value_loss = f.smooth_l1_loss(returns, value_pred).sum()
    return policy_loss, value_loss

Definieren der Ausbildungsschleife

Bevor du mit dem Training beginnst, erstelle eine Reihe von Puffern als leere Arrays. Der Trainingsalgorithmus verwendet diese Puffer, um Informationen über die Aktionen des Agenten, die Zustände der Umgebung und die Belohnungen in jedem Zeitschritt zu speichern. Die folgende Funktion initialisiert diese Puffer: 

def init_training():
    states = []
    actions = []
    actions_log_probability = []
    values = []
    rewards = []
    done = False
    episode_reward = 0
    return states, actions, actions_log_probability, values, rewards, done, episode_reward

Bei jeder Trainingsiteration wird der Agent mit den Parametern für die jeweilige Iteration ausgeführt. Der Agent interagiert mit der Umwelt in Zeitschritten in einer Schleife, bis er einen Endzustand erreicht. 

Nach jedem Zeitschritt werden die Aktion, die Belohnung und der Wert des Agenten an die jeweiligen Puffer angehängt. Wenn die Episode beendet ist, gibt die Funktion den aktualisierten Satz von Puffern zurück, der die Ergebnisse der Episode zusammenfasst. 

Bevor du die Trainingsschleife ausführst:

• Versetze das Modell mit agent.train() in den Trainingsmodus. 
• Setze die Umgebung mit env.reset() in einen zufälligen Zustand zurück. Dies ist der Ausgangszustand für diese Trainingsiteration. 

Die folgenden Schritte erklären, was in den einzelnen Zeitschritten der Trainingsschleife passiert: 

• Gib den Status an den Agenten weiter. 
• Der Agent kehrt zurück:
• Die vorhergesagte Aktion im gegebenen Zustand, basierend auf der Politik (Akteur). Führe diesen vorausgesagten Handlungstensor durch die Softmax-Funktion, um die Menge der Handlungswahrscheinlichkeiten zu erhalten.  
• Der vorhergesagte Wert des Zustands, basierend auf der Kritik.
• Der Agent wählt die zu ergreifende Aktion aus:
• Nutze die Aktionswahrscheinlichkeiten, um die Wahrscheinlichkeitsverteilung zu schätzen. 
• Wähle eine Aktion nach dem Zufallsprinzip aus, indem du eine Stichprobe aus dieser Verteilung ziehst. Dies geschieht mit der Funktion dist.sample(). 
• Verwende die Funktion env.step(), um diese Aktion an die Umgebung zu übergeben und die Reaktion der Umgebung für diesen Zeitschritt zu simulieren. Basierend auf der Aktion des Agenten erzeugt die Umgebung:
• Der neue Staat
• Die Belohnung
• Der boolesche Rückgabewert done (dieser zeigt an, ob die Umgebung einen Endzustand erreicht hat)
• Füge die Werte der Aktionen des Agenten, die Belohnungen, die vorhergesagten Werte und den neuen Zustand an die jeweiligen Puffer an. 

Die Trainingsepisode endet, wenn die Funktion env.step() für den booleschen Rückgabewert von done den Wert true zurückgibt. 

Nach Beendigung der Episode berechnest du anhand der kumulierten Werte aus jedem Zeitschritt den kumulativen Ertrag dieser Episode, indem du die Belohnungen aus jedem Zeitschritt addierst. Dazu verwenden wir die bereits beschriebene Funktion calculate_returns(). Die Eingaben dieser Funktion sind der Diskontierungsfaktor und der Puffer, der die Belohnungen aus jedem Zeitschritt enthält. Wir verwenden diese Renditen und die kumulierten Werte aus jedem Zeitschritt, um die Vorteile mithilfe der Funktion calculate_advantages() zu berechnen. 

Die folgende Python-Funktion zeigt, wie man diese Schritte umsetzt:

def forward_pass(env, agent, optimizer, discount_factor):
    states, actions, actions_log_probability, values, rewards, done, episode_reward = init_training()
    state = env.reset()
    agent.train()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        states.append(state)
        action_pred, value_pred = agent(state)
        action_prob = f.softmax(action_pred, dim=-1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)
        state, reward, done, _ = env.step(action.item())
        actions.append(action)
        actions_log_probability.append(log_prob_action)
        values.append(value_pred)
        rewards.append(reward)
        episode_reward += reward
    states = torch.cat(states)
    actions = torch.cat(actions)
    actions_log_probability = torch.cat(actions_log_probability)
    values = torch.cat(values).squeeze(-1)
    returns = calculate_returns(rewards, discount_factor)
    advantages = calculate_advantages(returns, values)
    return episode_reward, states, actions, actions_log_probability, advantages, returns

Aktualisieren der Modellparameter

Bei jeder Trainingsiteration durchläuft das Modell eine komplette Episode, die aus vielen Zeitschritten besteht (bis es einen Endzustand erreicht). In jedem Zeitschritt speichern wir die Politikparameter, die Aktionen des Agenten, die Erträge und die Vorteile. Nach jeder Iteration aktualisieren wir das Modell auf der Grundlage der Leistung der Politik in allen Zeitschritten dieser Iteration. 

Die maximale Anzahl von Zeitschritten in der CartPole Umgebung beträgt 500. In komplexeren Umgebungen gibt es mehr Zeitabschnitte, sogar Millionen. In solchen Fällen muss der Datensatz mit den Trainingsergebnissen in Stapel aufgeteilt werden. Die Anzahl der Zeitschritte in jedem Stapel wird als Optimierungsstapelgröße bezeichnet. 

Die Schritte zur Aktualisierung der Modellparameter sind also folgende:

• Teile den Datensatz mit den Trainingsergebnissen in Stapel auf. 
• Für jede Charge:
• Erhalte die Aktion des Agenten und den vorhergesagten Wert für jeden Zustand.
• Nutze diese vorhergesagten Aktionen, um die neue Aktionswahrscheinlichkeitsverteilung zu schätzen. 
• Verwende diese Verteilung, um die Entropie zu berechnen. 
• Verwende diese Verteilung, um die logarithmische Wahrscheinlichkeit der Aktionen im Trainingsdatensatz zu ermitteln. Dies ist der neue Satz logarithmischer Wahrscheinlichkeiten für die Aktionen im Datensatz der Trainingsergebnisse. Der alte Satz logarithmischer Wahrscheinlichkeiten für dieselben Handlungen wurde in der im vorherigen Abschnitt erläuterten Trainingsschleife berechnet. 
• Berechne den Ersatzverlust anhand der alten und neuen Wahrscheinlichkeitsverteilungen der Aktionen. 
• Berechne den Policenverlust und den Wertverlust anhand des Ersatzverlustes, der Entropie und der Vorteile. 
• Führe .backward() separat für die Police aus und bewerte die Verluste. Dadurch werden die Gradienten der Verlustfunktionen aktualisiert. 
• Führe .step() für den Optimierer aus, um die Richtlinienparameter zu aktualisieren. In diesem Fall verwenden wir den Adam-Optimierer, um ein Gleichgewicht zwischen Geschwindigkeit und Robustheit herzustellen. 
• Kumulieren Sie die Police und bewerten Sie Verluste. 
• Wiederhole den Rückwärtsdurchlauf (die oben genannten Vorgänge) für jede Charge ein paar Mal, je nach Wert des Parameters PPO_STEPS. Die Wiederholung des Rückwärtsdurchlaufs bei jedem Stapel ist rechnerisch effizient, weil dadurch die Größe des Trainingsdatensatzes effektiv erhöht wird, ohne dass zusätzliche Vorwärtsdurchläufe erforderlich sind. Die Anzahl der Umgebungsschritte bei jedem Wechsel zwischen Probenahme und Optimierung wird als Iterationsgröße bezeichnet. 
• Gib den durchschnittlichen Versicherungsschaden und den Wertverlust zurück.

Der folgende Code setzt diese Schritte um:

def update_policy(
        agent,
        states,
        actions,
        actions_log_probability_old,
        advantages,
        returns,
        optimizer,
        ppo_steps,
        epsilon,
        entropy_coefficient):
    BATCH_SIZE = 128
    total_policy_loss = 0
    total_value_loss = 0
    actions_log_probability_old = actions_log_probability_old.detach()
    actions = actions.detach()
    training_results_dataset = TensorDataset(
            states,
            actions,
            actions_log_probability_old,
            advantages,
            returns)
    batch_dataset = DataLoader(
            training_results_dataset,
            batch_size=BATCH_SIZE,
            shuffle=False)
    for _ in range(ppo_steps):
        for batch_idx, (states, actions, actions_log_probability_old, advantages, returns) in enumerate(batch_dataset):
            # get new log prob of actions for all input states
            action_pred, value_pred = agent(states)
            value_pred = value_pred.squeeze(-1)
            action_prob = f.softmax(action_pred, dim=-1)
            probability_distribution_new = distributions.Categorical(
                    action_prob)
            entropy = probability_distribution_new.entropy()
            # estimate new log probabilities using old actions
            actions_log_probability_new = probability_distribution_new.log_prob(actions)
            surrogate_loss = calculate_surrogate_loss(
                    actions_log_probability_old,
                    actions_log_probability_new,
                    epsilon,
                    advantages)
            policy_loss, value_loss = calculate_losses(
                    surrogate_loss,
                    entropy,
                    entropy_coefficient,
                    returns,
                    value_pred)
            optimizer.zero_grad()
            policy_loss.backward()
            value_loss.backward()
            optimizer.step()
            total_policy_loss += policy_loss.item()
            total_value_loss += value_loss.item()
    return total_policy_loss / ppo_steps, total_value_loss / ppo_steps

4. Den PPO-Agenten ausführen 

Lass uns endlich den PPO-Agenten testen.

Bewertung der Leistung 

Um die Leistung des Agenten zu bewerten, erstellst du eine neue Umgebung und berechnest die kumulierten Belohnungen aus dem Betrieb des Agenten in dieser neuen Umgebung. Du musst den Agenten mit der Funktion .eval() in den Evaluierungsmodus versetzen. Die Schritte sind die gleichen wie bei der Trainingsschleife. Der folgende Codeschnipsel implementiert die Bewertungsfunktion: 

def evaluate(env, agent):
    agent.eval()
    rewards = []
    done = False
    episode_reward = 0
    state = env.reset()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        with torch.no_grad():
            action_pred, _ = agent(state)
            action_prob = f.softmax(action_pred, dim=-1)
        action = torch.argmax(action_prob, dim=-1)
        state, reward, done, _ = env.step(action.item())
        episode_reward += reward
    return episode_reward

Trainingsergebnisse visualisieren

Wir werden die Matplotlib-Bibliothek verwenden, um den Fortschritt des Trainingsprozesses zu visualisieren. Die folgende Funktion zeigt, wie du die Belohnungen aus der Trainings- und der Testschleife aufzeichnen kannst:

def plot_train_rewards(train_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(train_rewards, label='Training Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Training Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(train_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

def plot_test_rewards(test_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(test_rewards, label='Testing Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Testing Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(test_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

In den Beispielgrafiken unten zeigen wir die Trainings- und Testbelohnungen, die sich aus der Anwendung der Richtlinie in der Trainings- bzw. Testumgebung ergeben. Beachte, dass die Form dieser Diagramme jedes Mal anders aussehen wird, wenn du den Code ausführst. Das liegt an der Zufälligkeit, die dem Trainingsprozess innewohnt. 

Trainingsbelohnungen (die durch die Anwendung der Strategie in der Trainingsumgebung erzielt werden). Bild vom Autor.

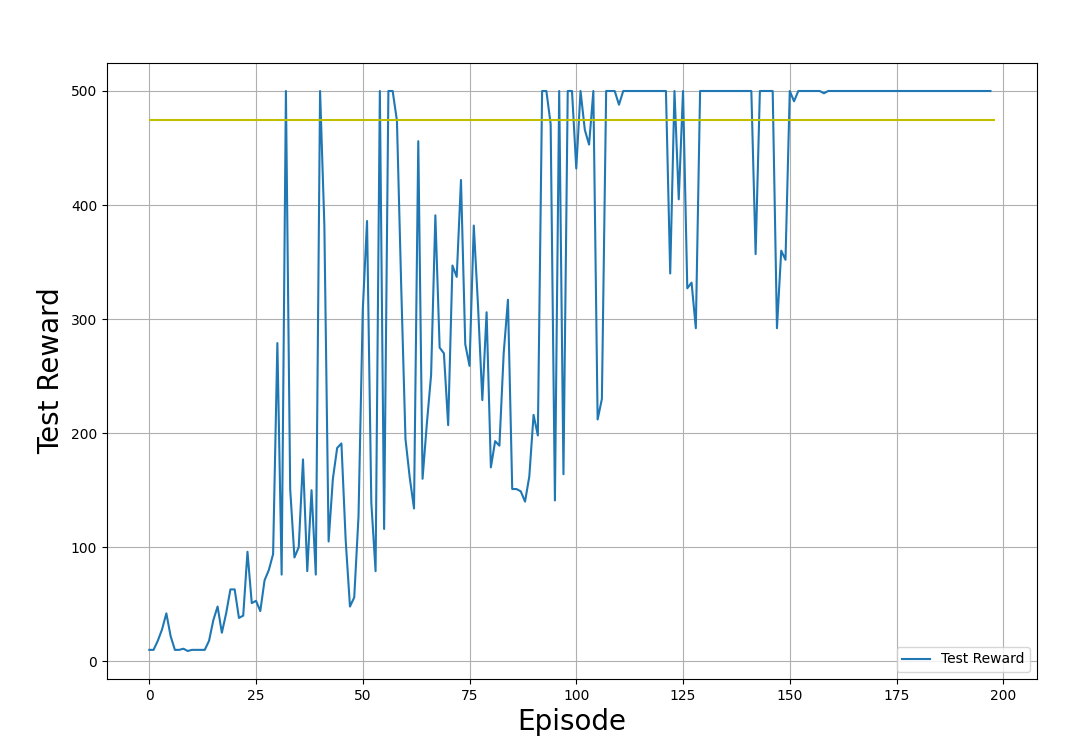
Testbelohnungen (die durch die Anwendung der Richtlinie in der Testumgebung erzielt werden). Bild vom Autor. 

In den oben gezeigten Ausgabegrafiken kannst du den Fortschritt des Trainingsprozesses beobachten:

• Die Belohnung beginnt bei niedrigen Werten. Je weiter das Training fortschreitet, desto größer werden die Belohnungen. 
• Die Belohnungen schwanken zufällig, während sie steigen. Das liegt daran, dass der Agent den Politikraum erkundet. 
• Das Training ist beendet, und die Testbelohnungen haben sich über viele Iterationen hinweg um den Schwellenwert (475) stabilisiert. 
• Die Belohnungen sind auf 500 begrenzt. Dies sind Einschränkungen, die von der Umgebung auferlegt werden (Gym CartPole v1). 

Ebenso kannst du den Wert und die Versicherungsverluste durch die Iterationen darstellen:

def plot_losses(policy_losses, value_losses):
    plt.figure(figsize=(12, 8))
    plt.plot(value_losses, label='Value Losses')
    plt.plot(policy_losses, label='Policy Losses')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Loss', fontsize=20)
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

Die folgende Beispielgrafik zeigt die Verluste, die durch die Lernpfade entstanden sind:

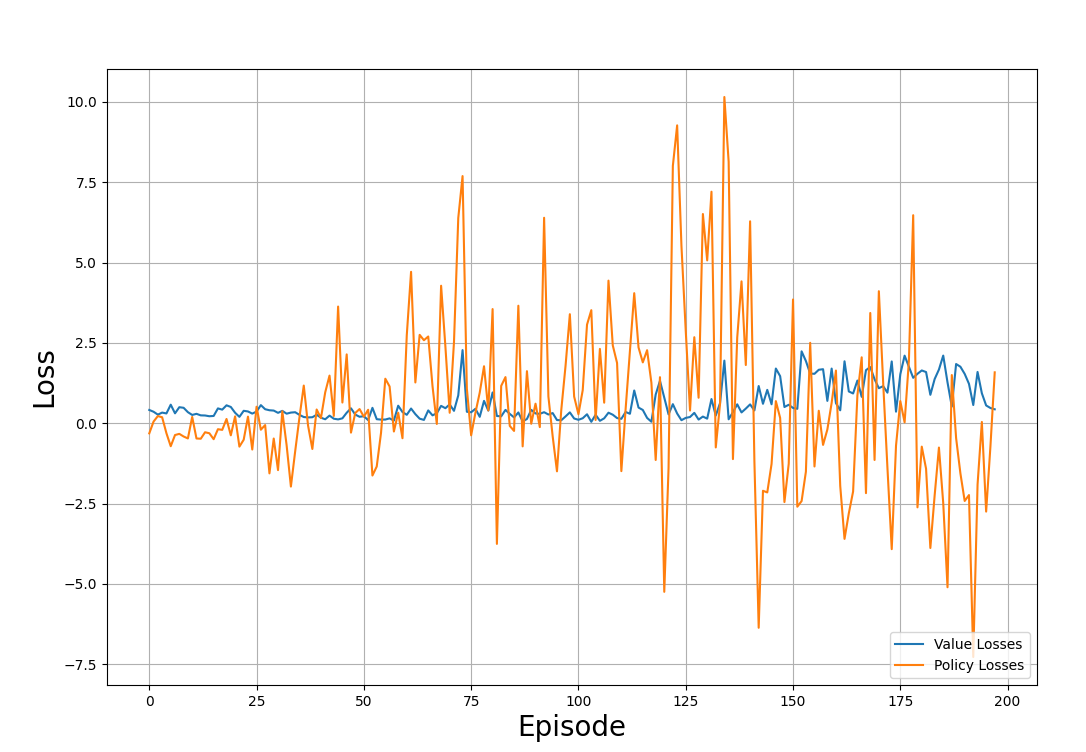
Wert- und Politikverluste durch den Ausbildungsprozess. Bild vom Autor

Beobachte die Handlung und beachte sie:

• Die Verluste scheinen zufällig verteilt zu sein und keinem Muster zu folgen. 
• Das ist typisch für das RL-Training, bei dem es nicht darum geht, den Verlust zu minimieren, sondern die Belohnung zu maximieren. 

Führe den PPO-Algorithmus aus

Du hast jetzt alle Komponenten, um den Agenten mit PPO zu schulen. Um das alles zusammenzufügen, musst du:

• Deklariere Hyperparameter wie Diskontierungsfaktor, Stapelgröße, Lernrate usw. 
• Instanziere Puffer als Null-Arrays, um die Belohnungen und Verluste aus jeder Iteration zu speichern. 
• Erstelle eine Agenteninstanz mit der Funktion create_agent().
• Führe iterativ Vorwärts- und Rückwärtsdurchläufe durch, indem du die Funktionen forward_pass() und update_policy() verwendest. 
• Teste die Leistung der Richtlinie mit der Funktion evaluate(). 
• Füge die Richtlinien, Wertverluste und Belohnungen aus den Trainings- und Bewertungsfunktionen zu den jeweiligen Puffern hinzu. 
• Berechne den Durchschnitt der Belohnungen und Verluste in den letzten paar Zeitschritten. Im folgenden Beispiel werden die Gewinne und Verluste der letzten 40 Zeitschritte gemittelt. 
• Drucke die Ergebnisse der Auswertung alle paar Schritte aus. Das folgende Beispiel druckt alle 10 Schritte. 
• Beende den Prozess, wenn die durchschnittliche Belohnung einen bestimmten Schwellenwert überschreitet. 

Der folgende Code zeigt, wie man in Python eine Funktion deklariert, die dies tut:

def run_ppo():
    MAX_EPISODES = 500
    DISCOUNT_FACTOR = 0.99
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    PPO_STEPS = 8
    N_TRIALS = 100
    EPSILON = 0.2
    ENTROPY_COEFFICIENT = 0.01
    HIDDEN_DIMENSIONS = 64
    DROPOUT = 0.2
    LEARNING_RATE = 0.001
    train_rewards = []
    test_rewards = []
    policy_losses = []
    value_losses = []
    agent = create_agent(HIDDEN_DIMENSIONS, DROPOUT)
    optimizer = optim.Adam(agent.parameters(), lr=LEARNING_RATE)
    for episode in range(1, MAX_EPISODES+1):
        train_reward, states, actions, actions_log_probability, advantages, returns = forward_pass(
                env_train,
                agent,
                optimizer,
                DISCOUNT_FACTOR)
        policy_loss, value_loss = update_policy(
                agent,
                states,
                actions,
                actions_log_probability,
                advantages,
                returns,
                optimizer,
                PPO_STEPS,
                EPSILON,
                ENTROPY_COEFFICIENT)
        test_reward = evaluate(env_test, agent)
        policy_losses.append(policy_loss)
        value_losses.append(value_loss)
        train_rewards.append(train_reward)
        test_rewards.append(test_reward)
        mean_train_rewards = np.mean(train_rewards[-N_TRIALS:])
        mean_test_rewards = np.mean(test_rewards[-N_TRIALS:])
        mean_abs_policy_loss = np.mean(np.abs(policy_losses[-N_TRIALS:]))
        mean_abs_value_loss = np.mean(np.abs(value_losses[-N_TRIALS:]))
        if episode % PRINT_INTERVAL == 0:
            print(f'Episode: {episode:3} | \
                  Mean Train Rewards: {mean_train_rewards:3.1f} \
                  | Mean Test Rewards: {mean_test_rewards:3.1f} \
                  | Mean Abs Policy Loss: {mean_abs_policy_loss:2.2f} \
                  | Mean Abs Value Loss: {mean_abs_value_loss:2.2f}')
        if mean_test_rewards >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break
    plot_train_rewards(train_rewards, REWARD_THRESHOLD)
    plot_test_rewards(test_rewards, REWARD_THRESHOLD)
    plot_losses(policy_losses, value_losses)

Führe das Programm aus: 

run_ppo()

Die Ausgabe sollte dem unten stehenden Beispiel ähneln: 

Episode:  10 | Mean Train Rewards: 22.3 | Mean Test Rewards: 30.4 | Mean Abs Policy Loss: 0.37 | Mean Abs Value Loss: 0.39 
Episode:  20 | Mean Train Rewards: 38.6 | Mean Test Rewards: 69.8 | Mean Abs Policy Loss: 0.46 | Mean Abs Value Loss: 0.37 
.
.
.
Episode: 100 | Mean Train Rewards: 289.5 | Mean Test Rewards: 427.3 | Mean Abs Policy Loss: 1.73 | Mean Abs Value Loss: 0.21 
Episode: 110 | Mean Train Rewards: 357.7 | Mean Test Rewards: 461.4 | Mean Abs Policy Loss: 1.86 | Mean Abs Value Loss: 0.22 
Reached reward threshold in 116 episodes

Du kannst das funktionierendeProgramm auf diesem DataLab-Notebookansehen und ausführen!

5. Hyperparameter-Abstimmung und -Optimierung

Beim maschinellen Lernen steuern die Hyperparameter den Trainingsprozess. Im Folgenden erkläre ich einige der wichtigen Hyperparameter, die im PPO verwendet werden: 

• Lernrate: Die Lernrate entscheidet darüber, wie stark die Parameter der Politik in jeder Iteration variieren können. Beim stochastischen Gradientenabstieg wird der Betrag, um den die Strategieparameter in jeder Iteration aktualisiert werden, durch das Produkt aus der Lernrate und dem Gradienten bestimmt. 
• Clipping-Parameter: Dies wird auch als Epsilon, ε, bezeichnet. Sie entscheidet darüber, in welchem Umfang die Politikquote gekappt wird. Das Verhältnis zwischen den neuen und den alten Policen darf in dem Bereich variieren [1-ε, 1+ε]. Wenn er außerhalb dieses Bereichs liegt, wird er künstlich beschnitten, damit er innerhalb des Bereichs liegt. 
• Chargengröße: Dies bezieht sich auf die Anzahl der Schritte, die für jede Gradientenaktualisierung berücksichtigt werden. In PPO ist die Losgröße die Anzahl der Zeitschritte, die benötigt werden, um die Politik anzuwenden und den Ersatzverlust zu berechnen, um die Politikparameter zu aktualisieren. In diesem Artikel haben wir eine Losgröße von 64 verwendet. 
• Iterationsschritte: Das ist die Anzahl, wie oft jeder Batch wiederverwendet wird, um den Rückwärtsdurchlauf durchzuführen. Der Code in diesem Artikel bezeichnet dies als PPO_STEPS. In komplexen Umgebungen ist es rechenintensiv, den Vorwärtsdurchlauf viele Male durchzuführen. Eine effizientere Alternative ist es, jeden Batch ein paar Mal zu wiederholen. In der Regel wird empfohlen, einen Wert zwischen 5 und 10 zu verwenden. 
• Rabattfaktor: Dies wird auch als Gamma, γ, bezeichnet. Er drückt aus, inwieweit unmittelbare Belohnungen wertvoller sind als zukünftige Belohnungen. Das ist ähnlich wie das Konzept der Zinssätze bei der Berechnung des Zeitwerts des Geldes. Wenn näher bei 0 liegt, bedeutet das, dass zukünftige Belohnungen weniger wertvoll sind und der Agent sofortige Belohnungen bevorzugen sollte. Wenn näher an 1 liegt, bedeutet das, dass zukünftige Belohnungen wichtig sind .
• Entropiekoeffizient: Der Entropiekoeffizient entscheidet über den Entropiebonus, der als Produkt aus dem Entropiekoeffizienten und der Entropie der Verteilung berechnet wird. Die Aufgabe des Entropie-Bonus ist es, mehr Zufälligkeit in die Politik zu bringen. Das ermutigt den Agenten, den Handlungsspielraum zu erkunden. Allerdings konvergiert das Training nicht zu einer optimalen Strategie, wenn diese Zufälligkeit zu hoch ist. 
• Erfolgskriterien für die Ausbildung: Du musst die Kriterien festlegen, anhand derer du entscheidest, wann das Training erfolgreich ist. Eine gängige Methode, dies zu tun, ist die Bedingung, dass die durchschnittlichen Belohnungen der letzten N Versuche (Episoden) über einem bestimmten Schwellenwert liegen. Im obigen Beispielcode wird dies durch die Variable N_TRIALS ausgedrückt. Wenn dieser Wert höher ist, dauert das Training länger, weil die Strategie den Schwellenwert für die Belohnung in mehr Episoden erreichen muss. Es führt auch zu einer robusteren Politik, ist aber rechenintensiver. Beachte, dass PPO eine stochastische Politik ist und es Episoden geben wird, in denen der Agent die Schwelle nicht überschreitet. Wenn also der Wert von N_TRIALS zu hoch ist, kann es sein, dass dein Training nicht beendet wird.

Strategien zur Optimierung der PPO-Leistung

Um die Leistung von PPO-Algorithmen zu optimieren, muss man mit verschiedenen Hyperparametern experimentieren und Fehler machen. Es gibt jedoch einige allgemeine Richtlinien: 

• Rabattfaktor: Wenn langfristige Belohnungen wichtig sind, wie in der CartPole-Umgebung, in der die Stange über einen längeren Zeitraum stabil bleiben muss, solltest du mit einem moderaten Gamma-Wert beginnen, z.B. mit 0,99. 
• Entropie-Bonus: In komplexen Umgebungen muss der Agent den Aktionsraum erkunden, um die optimale Strategie zu finden. Der Entropie-Bonus fördert die Erkundung. Der Entropie-Bonus wird zum Surrogatverlust addiert. Überprüfe die Höhe des Ersatzverlustes und die Entropie der Verteilung, bevor du den Entropiekoeffizienten festlegst. In diesem Artikel haben wir einen Entropiekoeffizienten von 0,01 verwendet.
• Clipping-Parameter: Der Clipping-Parameter bestimmt, wie sehr sich die aktualisierte Richtlinie von der aktuellen Richtlinie unterscheiden darf. Ein großer Wert des Clipping-Parameters fördert eine bessere Erkundung der Umgebung, birgt aber die Gefahr, dass das Training destabilisiert wird. Du willst einen Begrenzungsparameter, der eine schrittweise Erkundung ermöglicht und gleichzeitig destabilisierende Aktualisierungen verhindert. In diesem Artikel haben wir einen Clipping-Parameter von 0,2 verwendet.
• Lernrate: Wenn die Lernrate zu hoch ist, wird die Richtlinie in großen Schritten aktualisiert, und jede Iteration und der Trainingsprozess können instabil werden. Wenn er zu niedrig ist, dauert die Ausbildung zu lange.  In diesem Tutorium wurde eine Lernrate von 0,001 verwendet, was für die Umgebung gut funktioniert. In vielen Fällen ist es empfehlenswert, eine Lernrate von 1e-5 zu verwenden. 

Herausforderungen und bewährte Praktiken im PPO

Nachdem wir die Konzepte und die Einzelheiten der Umsetzung von PPO erläutert haben, wollen wir die Herausforderungen und die besten Praktiken diskutieren. 

Gemeinsame Herausforderungen bei der Ausbildung von PPO

Auch wenn PPO weit verbreitet ist, musst du dir der potenziellen Herausforderungen bewusst sein, um reale Probleme mit dieser Technik erfolgreich zu lösen. Einige dieser Herausforderungen sind:

• Langsame Konvergenz: In komplexen Umgebungen kann PPO stichprobenineffizient sein und benötigt viele Interaktionen mit der Umwelt, um zur optimalen Politik zu konvergieren. Das macht die Ausbildung langsam und teuer. 
• Empfindlichkeit gegenüber Hyperparametern: PPO beruht auf der effizienten Erkundung des politischen Raums. Die Stabilität des Trainingsprozesses und die Geschwindigkeit der Konvergenz hängen von den Werten der Hyperparameter ab. Die optimalen Werte dieser Hyperparameter können oft nur durch Versuch und Irrtum ermittelt werden. 
• Überanpassung:  RL-Umgebungen werden normalerweise mit zufälligen Parametern initialisiert. Beim PPO-Training geht es darum, die optimale Strategie auf der Grundlage der Umgebung des Agenten zu finden. Manchmal konvergiert der Trainingsprozess zu einem Satz optimaler Parameter für eine bestimmte Umgebung, aber nicht für eine zufällig ausgewählte Umgebung. Diesem Problem wird in der Regel durch viele Iterationen begegnet, bei denen jeweils eine andere Trainingsumgebung zufällig ausgewählt wird. 
• Dynamische Umgebungen: Einfache RL-Umgebungen, wie die CartPole-Umgebung, sind statisch - die Regeln sind immer dieselben. Viele andere Umgebungen, wie zum Beispiel ein Roboter, der lernt, auf einer instabilen Oberfläche zu laufen, sind dynamisch - die Regeln der Umgebung ändern sich mit der Zeit. Um in solchen Umgebungen gut abzuschneiden, muss das PPO oft noch feiner abgestimmt werden. 
• Erkundung vs. Ausbeutung: Der Clipping-Mechanismus von PPO stellt sicher, dass die Richtlinienaktualisierungen innerhalb einer vertrauenswürdigen Region stattfinden. Allerdings hindert es den Agenten auch daran, den Aktionsraum zu erkunden. Dies kann zu einer Konvergenz zu lokalen Optima führen, besonders in komplexen Umgebungen. Andererseits kann eine zu große Erkundungstiefe verhindern, dass der Agent zu einer optimalen Strategie konvergiert. 

Bewährte Praktiken für die Ausbildung von PPO-Modellen

Um mit PPO gute Ergebnisse zu erzielen, empfehle ich dir einige bewährte Methoden, wie zum Beispiel:

• Normalisiere die Eingangsmerkmale: Die Normalisierung der Werte von Renditen und Vorteilen reduziert die Variabilität der Daten und führt zu stabilen Gradientenaktualisierungen. Die Normalisierung der Daten bringt alle Werte in einen einheitlichen Zahlenbereich. Sie hilft, die Auswirkungen von Ausreißern und Extremwerten zu reduzieren, die andernfalls die Gradientenaktualisierungen verzerren und die Konvergenz verlangsamen könnten. 
• Verwende entsprechend große Chargengrößen: Kleine Stapel ermöglichen schnellere Aktualisierungen und Trainings, können aber zu einer Konvergenz zu lokalen Optima und Instabilität im Trainingsprozess führen. Größere Losgrößen ermöglichen es dem Agenten, robuste Richtlinien zu lernen, was zu einem stabilen Trainingsprozess führt. Zu große Losgrößen sind jedoch ebenfalls suboptimal. Sie erhöhen nicht nur die Rechenkosten, sondern führen auch dazu, dass die Aktualisierungen der Richtlinien weniger stark auf die Wertfunktion reagieren, da die Gradientenaktualisierungen auf Durchschnittswerten beruhen, die über große Stapel hinweg geschätzt werden. Außerdem kann es zu einer Überanpassung der Aktualisierungen an diese spezielle Charge führen. 
• Iterationsschritte: Es ist in der Regel ratsam, jeden Batch für 5-10 Iterationen zu verwenden. Das macht den Ausbildungsprozess effizienter. Wenn du denselben Stapel zu oft wiederholst, führt das zu einer Überanpassung. Im Code wird dieser Hyperparameter als PPO_STEPS bezeichnet. 
• Führe eine regelmäßige Bewertung durch: Um eine Überanpassung zu erkennen, ist es wichtig, die Wirksamkeit der Politik regelmäßig zu überprüfen. Wenn sich die Richtlinie in bestimmten Szenarien als unwirksam erweist, sind möglicherweise weitere Schulungen oder eine Feinabstimmung erforderlich. 
• Stimme die Hyperparameterab: Wie bereits erläutert, reagiert das PPO-Training empfindlich auf die Werte der Hyperparameter. Experimentiere mit verschiedenen Hyperparametern, um die richtigen Werte für dein spezielles Problem zu finden. 
• Gemeinsames Backbone-Netzwerk: Wie in diesem Artikel dargestellt, verhindert die Verwendung eines gemeinsamen Backbones Ungleichgewichte zwischen den Netzwerken der Akteure und der Kritiker. Die gemeinsame Nutzung eines Backbone-Netzwerks zwischen dem Akteur und dem Kritiker hilft bei der gemeinsamen Merkmalsextraktion und einem gemeinsamen Verständnis der Umgebung. Das macht den Lernprozess effizienter und stabiler. Außerdem hilft es, den Platz- und Zeitaufwand für den Algorithmus zu reduzieren. 
• Anzahl und Größe der versteckten Schichten: Erhöhe die Anzahl der versteckten Schichten und Dimensionen für komplexere Umgebungen. Einfachere Probleme wie CartPole können mit einer einzigen versteckten Schicht gelöst werden. Die in diesem Artikel verwendete versteckte Schicht hat 64 Dimensionen. Das Netzwerk viel größer als nötig zu machen, ist rechenaufwendig und kann es instabil machen. 
• Frühes Aufhören: Das Training wird gestoppt, wenn die Evaluierungskriterien erfüllt sind, um ein Übertraining zu verhindern und Ressourcenverschwendung zu vermeiden. Ein gängiger Bewertungsmaßstab ist, wenn der Agent die Schwellenwerte für die Belohnungen der letzten N Ereignisse überschreitet. 

Fazit

In diesem Artikel haben wir über PPO als eine Möglichkeit zur Lösung von RL-Problemen gesprochen. Anschließend haben wir die Schritte zur Implementierung von PPO mit PyTorch beschrieben. Zum Schluss haben wir noch einige Tipps und Best Practices für PPO vorgestellt. 

Am besten lernst du, indem du den Code selbst implementierst. Du kannst den Code auch so anpassen, dass er mit anderen klassischen Kontrollumgebungen in Gym funktioniert. Um zu lernen, wie man RL-Agenten mit Python und OpenAIs Gymnasium implementiert, besuche den Kurs Reinforcement Learning with Gymnasium in Python!