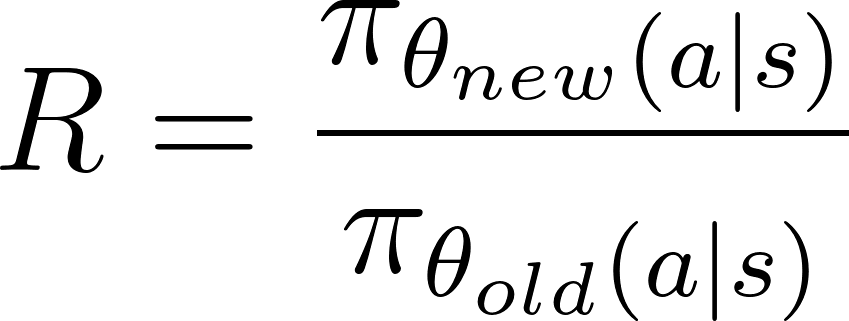Otimização de políticas proximais com PyTorch e Gymnasium

1. Configuração do ambiente 

Antes de implementar a PPO, precisamos instalar as bibliotecas de software de pré-requisito e escolher um ambiente adequado para aplicar a política. 

Instalação do PyTorch e das bibliotecas necessárias 

Precisamos instalar o seguinte software: 

• PyTorch e outras bibliotecas de software, como numpy (para funções matemáticas e estatísticas) e matplotlib (para plotagem de gráficos).
• O pacote de software de código aberto Gym da OpenAI, uma biblioteca Python que simula diferentes ambientes e jogos, que podem ser resolvidos usando o aprendizado por reforço. Você pode usar a API Gym para fazer com que seu algoritmo interaja com o ambiente. Como a funcionalidade do gym às vezes muda durante o processo de atualização, neste exemplo, congelamos sua versão para 0.25.2.

Para instalar em um servidor ou máquina local, execute: 

$ pip install torch numpy matplotlib gym==0.25.2

Para instalar usando um Notebook como o Google Colabou o DataLab, use: 

!pip install torch numpy matplotlib gym==0.25.2

Criar o(s) ambiente(s) do CartPole

Use o OpenAI Gym para criar duas instâncias (uma para treinamento e outra para teste) do ambiente do CartPole:

env_train = gym.make('CartPole-v1')
env_test = gym.make('CartPole-v1')

2. Implementação do PPO no PyTorch

Agora, vamos implementar o PPO usando o PyTorch.

Definição da rede de políticas

Conforme explicado anteriormente, o PPO é implementado como um modelo crítico de ator. O ator implementa a política, e o crítico prevê seu valor estimado. As redes neurais de ator e de crítico recebem a mesma entrada - o estado em cada intervalo de tempo. Assim, os modelos de ator e crítico podem compartilhar uma rede neural comum, que é chamada de arquitetura de backbone. O ator e o crítico podem estender a arquitetura de backbone com camadas adicionais. 

Definir a rede de backbone

As etapas a seguir descrevem a rede de backbone:

• Implemente uma rede com 3 camadas - uma de entrada, uma oculta e uma de saída. 
• Após as camadas de entrada e oculta, usamos uma função de ativação. Neste tutorial, escolhemos o ReLU porque ele é computacionalmente eficiente. 
• Também impomos uma função de abandono após as camadas de entrada e oculta para obter uma rede robusta. A função de abandono zera aleatoriamente alguns neurônios. Isso reduz a dependência de neurônios específicos e evita o ajuste excessivo, tornando a rede mais robusta. 

O código abaixo implementa o backbone:

class BackboneNetwork(nn.Module):
    def __init__(self, in_features, hidden_dimensions, out_features, dropout):
        super().__init__()
        self.layer1 = nn.Linear(in_features, hidden_dimensions)
        self.layer2 = nn.Linear(hidden_dimensions, hidden_dimensions)
        self.layer3 = nn.Linear(hidden_dimensions, out_features)
        self.dropout = nn.Dropout(dropout)
    def forward(self, x):
        x = self.layer1(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer2(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer3(x)
        return x

Definir a rede de atores-críticos

Agora, podemos usar essa rede para definir a classe de ator-crítico, ActorCritic. O ator modela a política e prevê a ação. O crítico modela a função de valor e prevê o valor. Ambos usam o estado como entrada. 

class ActorCritic(nn.Module):
    def __init__(self, actor, critic):
        super().__init__()
        self.actor = actor
        self.critic = critic
    def forward(self, state):
        action_pred = self.actor(state)
        value_pred = self.critic(state)
        return action_pred, value_pred

Instanciar as redes de atores e críticos

Usaremos as redes definidas acima para criar um ator e um crítico. Em seguida, criaremos um agente, incluindo o ator e o crítico. 

Antes de criar o agente, inicialize os parâmetros da rede:

• As dimensões da camada oculta, H, que é um parâmetro configurável. O tamanho e o número de camadas ocultas dependem da complexidade do problema. Usaremos uma camada oculta com dimensões de 64 x 64. 
• Recursos de entrada, N, em que N é o tamanho da matriz de estados. A camada de entrada tem dimensões N X H. No ambiente CartPole, o estado é uma matriz de 4 elementos. Portanto, N é 4. 
• Recursos de saída da rede de atores, O, em que O é o número de ações no ambiente. A camada de saída do ator tem dimensões H x O. O ambiente do CartPole tem 2 ações. 
• Recursos de saída da rede crítica. Como a rede crítica prevê apenas o valor esperado (dado um estado de entrada), o número de recursos de saída é 1. 
• Desistência como uma fração.

O código a seguir mostra como declarar o ator e as redes críticas com base na rede de backbone:

def create_agent(hidden_dimensions, dropout):
    INPUT_FEATURES = env_train.observation_space.shape[0]
    HIDDEN_DIMENSIONS = hidden_dimensions
    ACTOR_OUTPUT_FEATURES = env_train.action_space.n
    CRITIC_OUTPUT_FEATURES = 1
    DROPOUT = dropout
    actor = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, ACTOR_OUTPUT_FEATURES, DROPOUT)
    critic = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, CRITIC_OUTPUT_FEATURES, DROPOUT)
    agent = ActorCritic(actor, critic)
    return agent

Cálculo dos retornos

O ambiente oferece uma recompensa de cada etapa para a próxima, dependendo da ação do agente. A recompensa, R, é expressa como:

O retorno é definido como o valor acumulado das recompensas futuras esperadas. As recompensas de etapas de tempo mais distantes no futuro são menos valiosas do que as recompensas imediatas. Assim, o retorno é normalmente calculado como o retorno descontado, G, definido como:

Neste tutorial (e em muitas outras referências), retorno refere-se ao retorno descontado. 

Para calcular o retorno:

• Comece com as recompensas esperadas de todos os estados futuros.
• Multiplique cada recompensa futura por um expoente do fator de desconto, . Por exemplo, a recompensa esperada após 2 etapas de tempo (a partir do presente) é multiplicada por 2. 
• Some todas as recompensas futuras descontadas para calcular o retorno. 
• Normalize o valor do retorno. 

A função calculate_returns() realiza esses cálculos, conforme mostrado abaixo:

def calculate_returns(rewards, discount_factor):
    returns = []
    cumulative_reward = 0
    for r in reversed(rewards):
        cumulative_reward = r + cumulative_reward * discount_factor
        returns.insert(0, cumulative_reward)
    returns = torch.tensor(returns)
    # normalize the return
    returns = (returns - returns.mean()) / returns.std()
    return returns

Implementação da função de vantagem

A vantagem é calculada como a diferença entre o valor previsto pelo crítico e o retorno esperado das ações escolhidas pelo ator de acordo com a política. Para uma determinada ação, a vantagem expressa o benefício de realizar essa ação específica em relação a uma ação arbitrária (média). 

No documento original do PPO (equação 10), a vantagem, olhando para frente até o intervalo de tempo T, é expressa como:

Durante a codificação do algoritmo, a restrição de olhar para a frente até um número definido de passos de tempo é imposta por meio do tamanho do lote. Portanto, a equação acima pode ser simplificada como a diferença entre o valor e os retornos esperados. Os retornos esperados são quantificados na função de valor da ação do estado, Q. 

Assim, a fórmula simplificada abaixo expressa a vantagem da escolha: 

• uma ação específica 
• em um determinado estado 
• em uma determinada apólice 
• em um determinado intervalo de tempo 

Isso é expresso como: 

A OpenAI também usa essa fórmula para implementar a RL. Afunção calculate_advantages() mostrada abaixo calcula a vantagem:

def calculate_advantages(returns, values):
    advantages = returns - values
    # Normalize the advantage
    advantages = (advantages - advantages.mean()) / advantages.std()
    return advantages

Perda substituta e mecanismo de corte

A perda da apólice seria a perda padrão do gradiente da apólice sem técnicas especiais como PPO. A perda de gradiente da política padrão é calculada como o produto de:

• As probabilidades de ação da política 
• A função de vantagem, que é calculada como a diferença entre:
• A política de retorno 
• O valor esperado

A perda de gradiente de política padrão não pode fazer correções para mudanças abruptas de política. A perda substituta modifica a perda padrão para restringir o valor que a apólice pode alterar em cada iteração. É o mínimo de duas quantidades:

• O produto de:
• O índice de política. Essa proporção expressa a diferença entre as probabilidades de ação antiga e nova.  
• A função de vantagem 
• O produto de:
• O valor fixado do índice da política. Essa proporção é cortada de forma que a política atualizada esteja dentro de uma determinada porcentagem da política antiga. 
• A função de vantagem 

Para o processo de otimização, a perda substituta é usada como um substituto para a perda real. 

O mecanismo de recorte

O índice de política, Ré a diferença entre as políticas novas e antigas e é dada como a razão das probabilidades logarítmicas da política sob os parâmetros novos e antigos:

A taxa de política cortada, R'é limitado de forma que:

Dada a vantagem, Atconforme mostrado na seção anterior, e o índice de política, conforme mostrado acima, a perda substituta é calculada como:

O código abaixo mostra como implementar o mecanismo de recorte e a perda substituta. 

def calculate_surrogate_loss(
        actions_log_probability_old,
        actions_log_probability_new,
        epsilon,
        advantages):
    advantages = advantages.detach()
    policy_ratio = (
            actions_log_probability_new - actions_log_probability_old
            ).exp()
    surrogate_loss_1 = policy_ratio * advantages
    surrogate_loss_2 = torch.clamp(
            policy_ratio, min=1.0-epsilon, max=1.0+epsilon
            ) * advantages
    surrogate_loss = torch.min(surrogate_loss_1, surrogate_loss_2)
    return surrogate_loss

3. Treinamento do agente

Agora, vamos treinar o agente.

Cálculo da perda de valor e da apólice 

Agora estamos prontos para calcular a apólice e o valor das perdas: 

• A perda da apólice é a soma da perda substituta e do bônus de entropia. 
• Aperda de valoré baseada na diferença entre o valor previsto pelo crítico e os retornos (recompensa cumulativa) gerados pela apólice. O cálculo da perda de valor usa a função Smooth L1 Loss. Isso ajuda a suavizar a função de perda e a torna menos sensível a valores discrepantes.

Ambas as perdas, conforme computadas acima, são tensores. A descida de gradiente é baseada em valores escalares. Para obter um único valor escalar que represente a perda, use a função .sum() para somar os elementos do tensor. A função abaixo mostra como você pode fazer isso: 

def calculate_losses(
        surrogate_loss, entropy, entropy_coefficient, returns, value_pred):
    entropy_bonus = entropy_coefficient * entropy
    policy_loss = -(surrogate_loss + entropy_bonus).sum()
    value_loss = f.smooth_l1_loss(returns, value_pred).sum()
    return policy_loss, value_loss

Definição do loop de treinamento

Antes de iniciar o processo de treinamento, crie um conjunto de buffers como matrizes vazias. O algoritmo de treinamento usará esses buffers para armazenar informações sobre as ações do agente, os estados do ambiente e as recompensas em cada etapa de tempo. A função abaixo inicializa esses buffers: 

def init_training():
    states = []
    actions = []
    actions_log_probability = []
    values = []
    rewards = []
    done = False
    episode_reward = 0
    return states, actions, actions_log_probability, values, rewards, done, episode_reward

Cada iteração de treinamento executa o agente com os parâmetros de política para essa iteração. O agente interage com o ambiente em intervalos de tempo em um loop até atingir uma condição terminal. 

Após cada intervalo de tempo, a ação, a recompensa e o valor do agente são anexados aos respectivos buffers. Quando o episódio termina, a função retorna o conjunto atualizado de buffers, que resume os resultados do episódio. 

Antes de executar o loop de treinamento:

• Coloque o modelo no modo de treinamento usando agent.train(). 
• Redefina o ambiente para um estado aleatório usando env.reset(). Esse é o estado inicial para essa iteração de treinamento. 

As etapas a seguir explicam o que acontece em cada intervalo de tempo no loop de treinamento: 

• Passar o estado para o agente. 
• O agente retorna:
• A ação prevista, dado o estado, com base na política (ator). Passe esse tensor de ação previsto pela função softmax para obter o conjunto de probabilidades de ação.  
• O valor previsto do estado, com base no crítico.
• O agente seleciona a ação a ser tomada:
• Use as probabilidades de ação para estimar a distribuição de probabilidade. 
• Selecione aleatoriamente uma ação escolhendo uma amostra dessa distribuição. A função dist.sample() faz isso. 
• Use a função env.step() para passar essa ação para o ambiente e simular a resposta do ambiente para esse intervalo de tempo. Com base na ação do agente, o ambiente é gerado:
• O novo estado
• O prêmio
• O valor de retorno booleano done (isso indica se o ambiente atingiu um estado terminal)
• Anexe aos respectivos buffers os valores da ação do agente, as recompensas, os valores previstos e o novo estado. 

O episódio de treinamento termina quando a função env.step() retorna true para o valor de retorno booleano de done. 

Após o término do episódio, use os valores acumulados de cada etapa do tempo para calcular os retornos acumulados desse episódio, somando as recompensas de cada etapa do tempo. Para isso, usamos a função calculate_returns() descrita anteriormente. As entradas dessa função são o fator de desconto e o buffer que contém as recompensas de cada intervalo de tempo. Usamos esses retornos e os valores acumulados de cada intervalo de tempo para calcular as vantagens usando a função calculate_advantages(). 

A função Python a seguir mostra como você pode implementar essas etapas:

def forward_pass(env, agent, optimizer, discount_factor):
    states, actions, actions_log_probability, values, rewards, done, episode_reward = init_training()
    state = env.reset()
    agent.train()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        states.append(state)
        action_pred, value_pred = agent(state)
        action_prob = f.softmax(action_pred, dim=-1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)
        state, reward, done, _ = env.step(action.item())
        actions.append(action)
        actions_log_probability.append(log_prob_action)
        values.append(value_pred)
        rewards.append(reward)
        episode_reward += reward
    states = torch.cat(states)
    actions = torch.cat(actions)
    actions_log_probability = torch.cat(actions_log_probability)
    values = torch.cat(values).squeeze(-1)
    returns = calculate_returns(rewards, discount_factor)
    advantages = calculate_advantages(returns, values)
    return episode_reward, states, actions, actions_log_probability, advantages, returns

Atualização dos parâmetros do modelo

Cada iteração de treinamento executa o modelo por meio de um episódio completo que consiste em várias etapas de tempo (até atingir uma condição terminal). Em cada intervalo de tempo, armazenamos os parâmetros da política, a ação do agente, os retornos e as vantagens. Após cada iteração, atualizamos o modelo com base no desempenho da política em todos os intervalos de tempo dessa iteração. 

O número máximo de intervalos de tempo no ambiente do CartPole é 500. Em ambientes mais complexos, há mais etapas de tempo, até mesmo milhões. Nesses casos, o conjunto de dados dos resultados do treinamento deve ser dividido em lotes. O número de passos de tempo em cada lote é chamado de tamanho do lote de otimização. 

Assim, as etapas para atualizar os parâmetros do modelo são:

• Divida o conjunto de dados dos resultados do treinamento em lotes. 
• Para cada lote:
• Obtenha a ação do agente e o valor previsto para cada estado.
• Use essas ações previstas para estimar a nova distribuição de probabilidade de ação. 
• Use essa distribuição para calcular a entropia. 
• Use essa distribuição para obter a probabilidade de log das ações no conjunto de dados de resultados de treinamento. Esse é o novo conjunto de probabilidades de registro das ações no conjunto de dados de resultados de treinamento. O conjunto antigo de probabilidades de log dessas mesmas ações foi calculado no loop de treinamento explicado na seção anterior. 
• Calcule a perda substituta usando as distribuições de probabilidade antigas e novas das ações. 
• Calcule a perda da política e a perda de valor usando a perda substituta, a entropia e as vantagens. 
• Execute o site .backward() separadamente na apólice e avalie as perdas. Isso atualiza os gradientes das funções de perda. 
• Execute .step() no otimizador para atualizar os parâmetros da política. Nesse caso, usamos o otimizador Adam para equilibrar velocidade e robustez. 
• Acumular a apólice e valorizar as perdas. 
• Repita a passagem para trás (as operações acima) em cada lote algumas vezes, dependendo do valor do parâmetro PPO_STEPS. A repetição da passagem para trás em cada lote é computacionalmente eficiente porque aumenta efetivamente o tamanho do conjunto de dados de treinamento sem a necessidade de executar passagens para frente adicionais. O número de etapas do ambiente em cada alternância entre amostragem e otimização é chamado de tamanho do lote de iteração. 
• Retorne a perda média da apólice e a perda de valor.

O código abaixo implementa essas etapas:

def update_policy(
        agent,
        states,
        actions,
        actions_log_probability_old,
        advantages,
        returns,
        optimizer,
        ppo_steps,
        epsilon,
        entropy_coefficient):
    BATCH_SIZE = 128
    total_policy_loss = 0
    total_value_loss = 0
    actions_log_probability_old = actions_log_probability_old.detach()
    actions = actions.detach()
    training_results_dataset = TensorDataset(
            states,
            actions,
            actions_log_probability_old,
            advantages,
            returns)
    batch_dataset = DataLoader(
            training_results_dataset,
            batch_size=BATCH_SIZE,
            shuffle=False)
    for _ in range(ppo_steps):
        for batch_idx, (states, actions, actions_log_probability_old, advantages, returns) in enumerate(batch_dataset):
            # get new log prob of actions for all input states
            action_pred, value_pred = agent(states)
            value_pred = value_pred.squeeze(-1)
            action_prob = f.softmax(action_pred, dim=-1)
            probability_distribution_new = distributions.Categorical(
                    action_prob)
            entropy = probability_distribution_new.entropy()
            # estimate new log probabilities using old actions
            actions_log_probability_new = probability_distribution_new.log_prob(actions)
            surrogate_loss = calculate_surrogate_loss(
                    actions_log_probability_old,
                    actions_log_probability_new,
                    epsilon,
                    advantages)
            policy_loss, value_loss = calculate_losses(
                    surrogate_loss,
                    entropy,
                    entropy_coefficient,
                    returns,
                    value_pred)
            optimizer.zero_grad()
            policy_loss.backward()
            value_loss.backward()
            optimizer.step()
            total_policy_loss += policy_loss.item()
            total_value_loss += value_loss.item()
    return total_policy_loss / ppo_steps, total_value_loss / ppo_steps

4. Execução do agente PPO 

Finalmente, vamos executar o agente PPO.

Avaliação do desempenho 

Para avaliar o desempenho do agente, crie um novo ambiente e calcule as recompensas cumulativas da execução do agente nesse novo ambiente. Você precisa definir o agente para o modo de avaliação usando a função .eval(). As etapas são as mesmas do loop de treinamento. O trecho de código abaixo implementa a função de avaliação: 

def evaluate(env, agent):
    agent.eval()
    rewards = []
    done = False
    episode_reward = 0
    state = env.reset()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        with torch.no_grad():
            action_pred, _ = agent(state)
            action_prob = f.softmax(action_pred, dim=-1)
        action = torch.argmax(action_prob, dim=-1)
        state, reward, done, _ = env.step(action.item())
        episode_reward += reward
    return episode_reward

Visualização dos resultados do treinamento

Usaremos a biblioteca Matplotlib para visualizar o progresso do processo de treinamento. A função abaixo mostra como plotar as recompensas dos loops de treinamento e teste:

def plot_train_rewards(train_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(train_rewards, label='Training Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Training Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(train_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

def plot_test_rewards(test_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(test_rewards, label='Testing Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Testing Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(test_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

Nos gráficos de exemplo abaixo, mostramos as recompensas de treinamento e teste, obtidas pela aplicação da política nos ambientes de treinamento e teste, respectivamente. Observe que a forma desses gráficos parecerá diferente toda vez que você executar o código. Isso se deve à aleatoriedade inerente ao processo de treinamento. 

Recompensas de treinamento (obtidas pela aplicação da política no ambiente de treinamento). Imagem do autor.

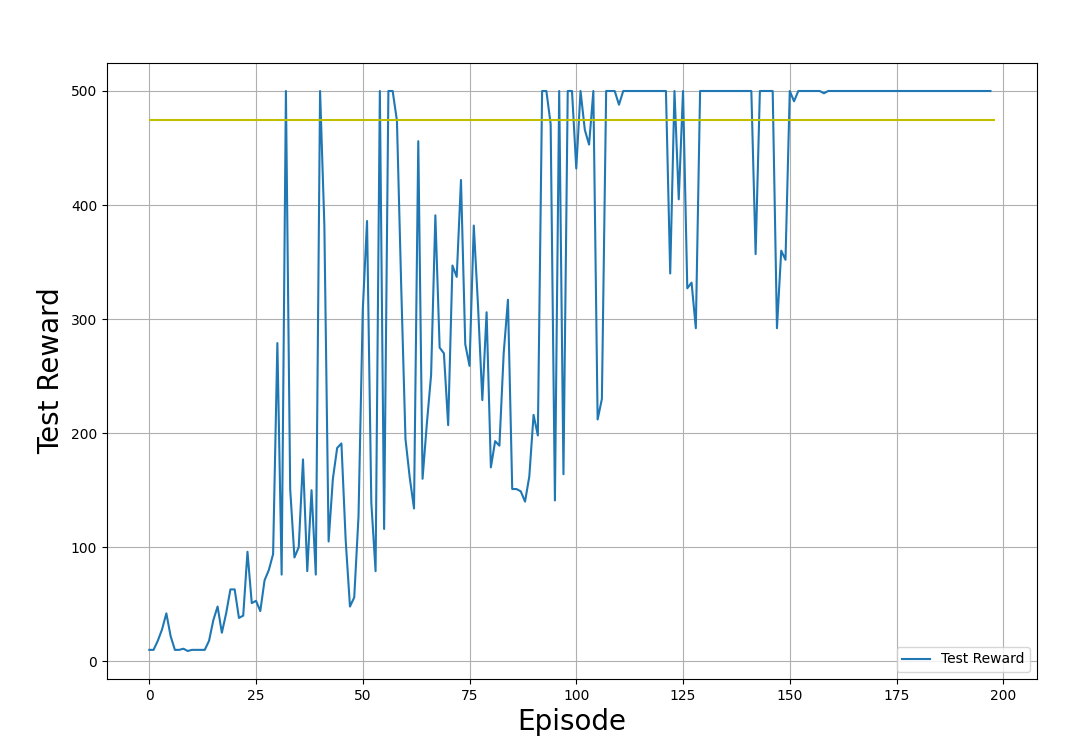
Recompensas de teste (obtidas pela aplicação da política no ambiente de teste). Imagem do autor. 

Nos gráficos de saída mostrados acima, observe o progresso do processo de treinamento:

• A recompensa começa com valores baixos. À medida que o treinamento avança, as recompensas aumentam. 
• As recompensas flutuam aleatoriamente enquanto aumentam. Isso se deve ao fato de o agente explorar o espaço da política. 
• O treinamento termina e as recompensas do teste se estabilizaram em torno do limite (475) por muitas iterações. 
• As recompensas são limitadas a 500. Essas são restrições impostas pelo ambiente (Gym CartPole v1). 

Da mesma forma, você pode traçar o valor e as perdas da apólice por meio das iterações:

def plot_losses(policy_losses, value_losses):
    plt.figure(figsize=(12, 8))
    plt.plot(value_losses, label='Value Losses')
    plt.plot(policy_losses, label='Policy Losses')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Loss', fontsize=20)
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

O gráfico de exemplo abaixo mostra as perdas rastreadas nos episódios de treinamento:

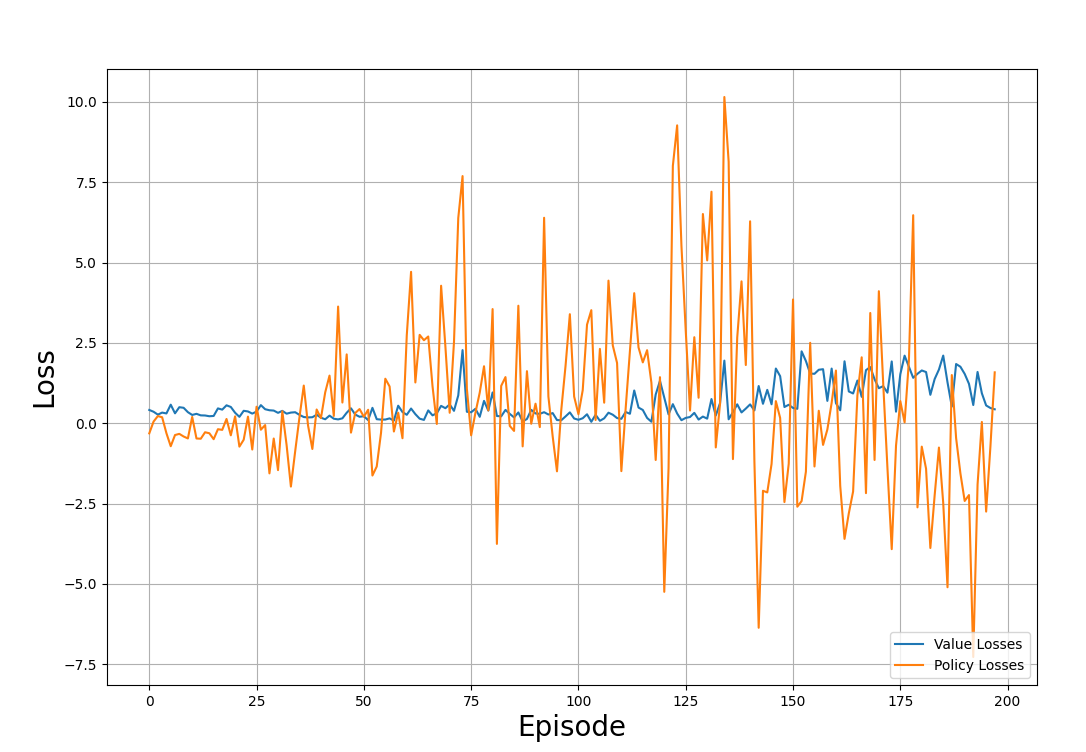
Perdas de valor e de política por meio do processo de treinamento. Imagem do autor

Observe o enredo e perceba:

• As perdas parecem ser distribuídas aleatoriamente e não seguem nenhum padrão. 
• Isso é típico do treinamento de RL, em que o objetivo não é minimizar a perda, mas maximizar as recompensas. 

Executar o algoritmo PPO

Agora você tem todos os componentes para treinar o agente usando o PPO. Para juntar tudo isso, você precisa:

• Declare os hiperparâmetros, como fator de desconto, tamanho do lote, taxa de aprendizado, etc. 
• Instanciar buffers como matrizes nulas para armazenar as recompensas e perdas de cada iteração. 
• Crie uma instância de agente usando a função create_agent().
• Execute iterativamente passagens para frente e para trás usando as funções forward_pass() e update_policy(). 
• Teste o desempenho da política usando a função evaluate(). 
• Anexe a política, as perdas de valor e as recompensas das funções de treinamento e avaliação aos respectivos buffers. 
• Calcule a média das recompensas e perdas nas últimas etapas de tempo. O exemplo abaixo calcula a média dos prêmios e perdas nas últimas 40 etapas de tempo. 
• Imprima os resultados da avaliação a cada poucas etapas. O exemplo abaixo imprime a cada 10 etapas. 
• Encerre o processo quando a recompensa média ultrapassar um determinado limite. 

O código abaixo mostra como você pode declarar uma função que faz isso no Python:

def run_ppo():
    MAX_EPISODES = 500
    DISCOUNT_FACTOR = 0.99
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    PPO_STEPS = 8
    N_TRIALS = 100
    EPSILON = 0.2
    ENTROPY_COEFFICIENT = 0.01
    HIDDEN_DIMENSIONS = 64
    DROPOUT = 0.2
    LEARNING_RATE = 0.001
    train_rewards = []
    test_rewards = []
    policy_losses = []
    value_losses = []
    agent = create_agent(HIDDEN_DIMENSIONS, DROPOUT)
    optimizer = optim.Adam(agent.parameters(), lr=LEARNING_RATE)
    for episode in range(1, MAX_EPISODES+1):
        train_reward, states, actions, actions_log_probability, advantages, returns = forward_pass(
                env_train,
                agent,
                optimizer,
                DISCOUNT_FACTOR)
        policy_loss, value_loss = update_policy(
                agent,
                states,
                actions,
                actions_log_probability,
                advantages,
                returns,
                optimizer,
                PPO_STEPS,
                EPSILON,
                ENTROPY_COEFFICIENT)
        test_reward = evaluate(env_test, agent)
        policy_losses.append(policy_loss)
        value_losses.append(value_loss)
        train_rewards.append(train_reward)
        test_rewards.append(test_reward)
        mean_train_rewards = np.mean(train_rewards[-N_TRIALS:])
        mean_test_rewards = np.mean(test_rewards[-N_TRIALS:])
        mean_abs_policy_loss = np.mean(np.abs(policy_losses[-N_TRIALS:]))
        mean_abs_value_loss = np.mean(np.abs(value_losses[-N_TRIALS:]))
        if episode % PRINT_INTERVAL == 0:
            print(f'Episode: {episode:3} | \
                  Mean Train Rewards: {mean_train_rewards:3.1f} \
                  | Mean Test Rewards: {mean_test_rewards:3.1f} \
                  | Mean Abs Policy Loss: {mean_abs_policy_loss:2.2f} \
                  | Mean Abs Value Loss: {mean_abs_value_loss:2.2f}')
        if mean_test_rewards >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break
    plot_train_rewards(train_rewards, REWARD_THRESHOLD)
    plot_test_rewards(test_rewards, REWARD_THRESHOLD)
    plot_losses(policy_losses, value_losses)

Execute o programa: 

run_ppo()

O resultado deve ser semelhante ao exemplo abaixo: 

Episode:  10 | Mean Train Rewards: 22.3 | Mean Test Rewards: 30.4 | Mean Abs Policy Loss: 0.37 | Mean Abs Value Loss: 0.39 
Episode:  20 | Mean Train Rewards: 38.6 | Mean Test Rewards: 69.8 | Mean Abs Policy Loss: 0.46 | Mean Abs Value Loss: 0.37 
.
.
.
Episode: 100 | Mean Train Rewards: 289.5 | Mean Test Rewards: 427.3 | Mean Abs Policy Loss: 1.73 | Mean Abs Value Loss: 0.21 
Episode: 110 | Mean Train Rewards: 357.7 | Mean Test Rewards: 461.4 | Mean Abs Policy Loss: 1.86 | Mean Abs Value Loss: 0.22 
Reached reward threshold in 116 episodes

Você pode visualizar e executar oprograma em funcionamento neste notebook do DataLab!

5. Ajuste e otimização de hiperparâmetros

No aprendizado de máquina, os hiperparâmetros controlam o processo de treinamento. A seguir, explico alguns dos hiperparâmetros importantes usados no PPO: 

• Taxa de aprendizado: A taxa de aprendizado decide o quanto os parâmetros da política podem variar em cada iteração. Na descida gradiente estocástica, o valor pelo qual os parâmetros da política são atualizados em cada iteração é decidido pelo produto da taxa de aprendizado e do gradiente. 
• Parâmetro de recorte: Isso também é chamado de épsilon, ε. Ele decide até que ponto o índice da política é cortado. É permitido que a proporção das apólices novas e antigas varie no intervalo [1-ε, 1+ε]. Quando está além desse intervalo, ele é artificialmente cortado para ficar dentro do intervalo. 
• Tamanho do lote: Refere-se ao número de etapas a serem consideradas para cada atualização de gradiente. Na PPO, o tamanho do lote é o número de etapas de tempo necessárias para aplicar a política e calcular a perda substituta para atualizar os parâmetros da política. Neste artigo, usamos um tamanho de lote de 64. 
• Etapas de iteração: Esse é o número de vezes que cada lote é reutilizado para executar a passagem para trás. O código neste artigo se refere a isso como PPO_STEPS. Em ambientes complexos, a execução da passagem direta várias vezes é computacionalmente cara. Uma alternativa mais eficiente é executar novamente cada lote algumas vezes. Normalmente, recomenda-se que você use um valor entre 5 e 10. 
• Fator de desconto: Isso também é chamado de gama, γ. Ele expressa o grau em que as recompensas imediatas são mais valiosas do que as recompensas futuras. Isso é semelhante ao conceito de taxas de juros no cálculo do valor do dinheiro no tempo. Quando está mais próximo de 0, isso significa que as recompensas futuras são menos valiosas e o agente deve priorizar as recompensas imediatas. Quando está mais próximo de 1, significa que as recompensas futuras são importantes .
• Coeficiente de entropia: O coeficiente de entropia decide o bônus de entropia, que é calculado como o produto do coeficiente de entropia e a entropia da distribuição. A função do bônus de entropia é introduzir mais aleatoriedade na política. Isso incentiva o agente a explorar o espaço da política. No entanto, o treinamento não converge para uma política ideal quando essa aleatoriedade é muito alta. 
• Critérios de sucesso para o treinamento: Você precisa definir os critérios para decidir quando o treinamento é bem-sucedido. Uma maneira comum de fazer isso é colocar a condição de que as recompensas médias das últimas N tentativas (episódios) estejam acima de um determinado limite. No código de exemplo acima, isso é expresso com a variável N_TRIALS. Quando esse valor é definido como mais alto, o treinamento é mais demorado porque a política precisa atingir a recompensa limite em mais episódios. Isso também resulta em uma política mais robusta, embora seja computacionalmente mais cara. Observe que a PPO é uma política estocástica, e haverá episódios em que o agente não ultrapassará o limite. Portanto, se o valor de N_TRIALS for muito alto, o treinamento poderá não terminar.

Estratégias para otimizar o desempenho da PPO

A otimização do desempenho dos algoritmos de PPO de treinamento envolve tentativa e erro e experimentos com diferentes valores de hiperparâmetro. No entanto, existem algumas diretrizes gerais: 

• Fator de desconto: Quando as recompensas de longo prazo forem importantes, como no ambiente do CartPole, em que o polo precisa permanecer estável ao longo do tempo, comece com um valor de gama moderado, como 0,99. 
• Bônus de entropia: Em ambientes complexos, o agente deve explorar o espaço de ação para encontrar a política ideal. O bônus de entropia promove a exploração. O bônus de entropia é adicionado à perda substituta. Verifique a magnitude da perda substituta e a entropia da distribuição antes de decidir o coeficiente de entropia. Neste artigo, usamos um coeficiente de entropia de 0,01.
• Parâmetro de recorte: O parâmetro de recorte decide o quanto a política atualizada pode ser diferente da política atual. Um valor grande do parâmetro de recorte incentiva uma melhor exploração do ambiente, mas corre o risco de desestabilizar o treinamento. Você deseja um parâmetro de recorte que permita a exploração gradual e, ao mesmo tempo, evite atualizações desestabilizadoras. Neste artigo, usamos um parâmetro de recorte de 0,2.
• Taxa de aprendizado: Quando a taxa de aprendizado é muito alta, a política é atualizada em etapas grandes, e cada iteração e o processo de treinamento podem se tornar instáveis. Quando o valor é muito baixo, o treinamento demora muito.  Este tutorial usou uma taxa de aprendizado de 0,001, que funciona bem para o ambiente. Em muitos casos, é recomendável usar uma taxa de aprendizado de 1e-5. 

Desafios e práticas recomendadas em PPO

Depois de explicar os conceitos da PPO e os detalhes da implementação, vamos discutir os desafios e as práticas recomendadas. 

Desafios comuns no treinamento de PPO

Embora a PPO seja amplamente usada, você precisa estar ciente dos possíveis desafios para resolver problemas do mundo real usando essa técnica com sucesso. Alguns desses desafios são:

• Convergência lenta: Em ambientes complexos, a PPO pode ser ineficiente em termos de amostragem e precisa de muitas interações com o ambiente para convergir para a política ideal. Isso torna o treinamento lento e caro. 
• Sensibilidade aos hiperparâmetros: A PPO se baseia na exploração eficiente do espaço da política. A estabilidade do processo de treinamento e a velocidade de convergência são sensíveis aos valores dos hiperparâmetros. Os valores ideais desses hiperparâmetros geralmente só podem ser determinados por tentativa e erro. 
• Ajuste excessivo:  Em geral, os ambientes de RL são inicializados com parâmetros aleatórios. O treinamento de PPO baseia-se em encontrar a política ideal com base no ambiente do agente. Às vezes, o processo de treinamento converge para um conjunto de parâmetros ideais para um ambiente específico, mas não para qualquer ambiente aleatório. Normalmente, isso é resolvido por meio de várias iterações, cada uma com um ambiente de treinamento diferente e aleatório. 
• Ambientes dinâmicos: Ambientes simples de RL, como o ambiente do CartPole, são estáticos - as regras são as mesmas ao longo do tempo. Muitos outros ambientes, como um robô que aprende a andar em uma superfície móvel instável, são dinâmicos - as regras do ambiente mudam com o tempo. Para ter um bom desempenho em tais ambientes, o PPO geralmente precisa de um ajuste fino adicional. 
• Exploração vs. exploração: O mecanismo de recorte do PPO garante que as atualizações de política estejam dentro de uma região confiável. No entanto, isso também impede que o agente explore o espaço de ação. Isso pode levar à convergência para ótimos locais, especialmente em ambientes complexos. Por outro lado, permitir que o agente explore demais pode impedi-lo de convergir para uma política ótima. 

Práticas recomendadas para treinamento de modelos de PPO

Para que você obtenha bons resultados usando o PPO, recomendo algumas práticas recomendadas, como

• Normalize os recursos de entrada: A normalização dos valores de retornos e vantagens reduz a variabilidade dos dados e leva a atualizações estáveis do gradiente. A normalização dos dados coloca todos os valores em um intervalo numérico consistente. Isso ajuda a reduzir o efeito de valores extremos e discrepantes, que poderiam distorcer as atualizações de gradiente e retardar a convergência. 
• Use tamanhos de lote adequadamente grandes: Pequenos lotes permitem atualizações e treinamento mais rápidos, mas podem levar à convergência para ótimos locais e à instabilidade no processo de treinamento. Os lotes maiores permitem que o agente aprenda políticas robustas, o que leva a um processo de treinamento estável. No entanto, tamanhos de lote muito grandes também não são ideais. Além de aumentar os custos de computação, eles tornam as atualizações de política menos sensíveis à função de valor porque as atualizações de gradiente são baseadas em médias estimadas em grandes lotes. Além disso, isso pode levar ao ajuste excessivo das atualizações a esse lote específico. 
• Etapas de iteração: Em geral, é recomendável reutilizar cada lote para 5 a 10 iterações. Isso torna o processo de treinamento mais eficiente. A reutilização do mesmo lote muitas vezes leva a um ajuste excessivo. O código se refere a esse hiperparâmetro como PPO_STEPS. 
• Faça avaliações regulares: Para detectar o ajuste excessivo, é essencial monitorar periodicamente a eficácia da política. Se a política se mostrar ineficaz em determinados cenários, poderá ser necessário um treinamento adicional ou um ajuste fino. 
• Ajuste os hiperparâmetros: Conforme explicado anteriormente, o treinamento do PPO é sensível aos valores dos hiperparâmetros. Faça experiências com vários valores de hiperparâmetros para determinar o conjunto certo de valores para seu problema específico. 
• Rede de backbone compartilhada: Conforme ilustrado neste artigo, o uso de um backbone compartilhado evita desequilíbrios entre as redes de atores e de críticos. O compartilhamento de uma rede de backbone entre o ator e o crítico ajuda na extração de recursos compartilhados e em um entendimento comum do ambiente. Isso torna o processo de aprendizado mais eficiente e estável. Isso também ajuda a reduzir o espaço computacional e a complexidade de tempo do algoritmo. 
• Número e tamanho das camadas ocultas: Aumente o número de camadas e dimensões ocultas para ambientes mais complexos. Problemas mais simples, como o CartPole, podem ser resolvidos com uma única camada oculta. A camada oculta usada neste artigo tem 64 dimensões. Tornar a rede muito maior do que o necessário é um desperdício computacional e pode torná-la instável. 
• Parada precoce: Interromper o treinamento quando as métricas de avaliação são atendidas ajuda a evitar o excesso de treinamento e evita o desperdício de recursos. Uma métrica de avaliação comum é quando o agente excede o limite de recompensas nos últimos N eventos. 

Conclusão

Neste artigo, discutimos a PPO como uma forma de resolver problemas de RL. Em seguida, detalhamos as etapas para implementar o PPO usando o PyTorch. Por fim, apresentamos algumas dicas de desempenho e práticas recomendadas para PPO. 

A melhor maneira de aprender é você mesmo implementar o código. Você também pode modificar o código para trabalhar com outros ambientes de controle clássicos no Gym. Para saber como implementar agentes de RL usando Python e o Gymnasium da OpenAI, siga o curso Reinforcement Learning with Gymnasium in Python!