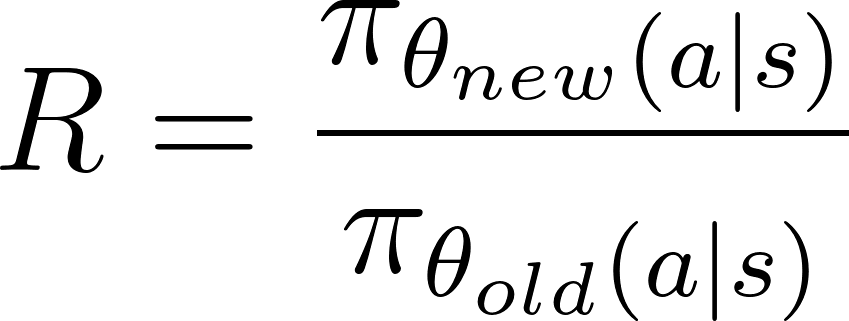Proximal Policy Optimization with PyTorch and Gymnasium

1. Setting Up the Environment 

Before implementing PPO, we need to install the prerequisite software libraries and choose a suitable environment to apply the policy. 

Installing PyTorch and required libraries 

We need to install the following software: 

• PyTorch and other software libraries, such as numpy (for mathematical and statistical functions) and matplotlib (for plotting graphs).
• The open-source Gym software package from OpenAI, a Python library that simulates different environments and games, which can be solved using Reinforcement learning. You can use the Gym API to get your algorithm to interact with the environment. Since the functionality of gym sometimes changes through the upgrade process, in this example, we freeze its version to 0.25.2.

To install on a server or local machine, run: 

$ pip install torch numpy matplotlib gym==0.25.2

To install using a Notebook like Google Colab or DataLab, use: 

!pip install torch numpy matplotlib gym==0.25.2

Create the CartPole environment(s)

Use OpenAI Gym to create two instances (one for training and another for testing) of the CartPole environment:

env_train = gym.make('CartPole-v1')
env_test = gym.make('CartPole-v1')

2. Implementing PPO in PyTorch

Now, let’s implement PPO using PyTorch.

Defining the policy network

As explained earlier, PPO is implemented as an actor-critic model. The actor implements the policy, and the critic predicts its estimated value. Both actor and critic neural networks take the same input—the state at each timestep. Thus, the actor and critic models can share a common neural network, which is referred to as the backbone architecture. The actor and critic can extend the backbone architecture with additional layers. 

Define the backbone network

The following steps describe the backbone network:

• Implement a network with 3 layers - an input, a hidden, and an output layer. 
• After the input and hidden layers, we use an activation function. In this tutorial, we choose ReLU because it is computationally efficient. 
• We also impose a dropout function after the input and hidden layers to obtain a robust network. The dropout function randomly zeros some neurons. This reduces reliance on specific neurons and prevents overfitting, thus making the network more robust. 

The code below implements the backbone:

class BackboneNetwork(nn.Module):
    def __init__(self, in_features, hidden_dimensions, out_features, dropout):
        super().__init__()
        self.layer1 = nn.Linear(in_features, hidden_dimensions)
        self.layer2 = nn.Linear(hidden_dimensions, hidden_dimensions)
        self.layer3 = nn.Linear(hidden_dimensions, out_features)
        self.dropout = nn.Dropout(dropout)
    def forward(self, x):
        x = self.layer1(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer2(x)
        x = f.relu(x)
        x = self.dropout(x)
        x = self.layer3(x)
        return x

Define the actor-critic network

Now, we can use this network to define the actor-critic class, ActorCritic. The actor models the policy and predicts the action. The critic models the value function and predicts the value. They both take the state as input. 

class ActorCritic(nn.Module):
    def __init__(self, actor, critic):
        super().__init__()
        self.actor = actor
        self.critic = critic
    def forward(self, state):
        action_pred = self.actor(state)
        value_pred = self.critic(state)
        return action_pred, value_pred

Instantiate the actor and critic networks

We’ll use the networks defined above to create an actor and a critic. Then, we will create an agent, including the actor and the critic. 

Before creating the agent, initialize the parameters of the network:

• The hidden layer's dimensions, H, which is a configurable parameter. The size and number of hidden layers depend on the complexity of the problem. We will use a hidden layer with 64 X 64 dimensions. 
• Input features, N, where N is the size of the state array. The input layer has N X H dimensions. In the CartPole environment, the state is a 4-element array. So N is 4. 
• Output features of the actor network, O, where O is the number of actions in the environment. The actor's output layer has H x O dimensions. The CartPole environment has 2 actions. 
• Output features of the critic network. Since the critic network predicts just the expected value (given an input state), the number of output features is 1. 
• Dropout as a fraction.

The following code shows how to declare the actor and critic networks based on the backbone network:

def create_agent(hidden_dimensions, dropout):
    INPUT_FEATURES = env_train.observation_space.shape[0]
    HIDDEN_DIMENSIONS = hidden_dimensions
    ACTOR_OUTPUT_FEATURES = env_train.action_space.n
    CRITIC_OUTPUT_FEATURES = 1
    DROPOUT = dropout
    actor = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, ACTOR_OUTPUT_FEATURES, DROPOUT)
    critic = BackboneNetwork(
            INPUT_FEATURES, HIDDEN_DIMENSIONS, CRITIC_OUTPUT_FEATURES, DROPOUT)
    agent = ActorCritic(actor, critic)
    return agent

Calculating the returns

The environment gives a reward going from each step to the next, depending on the agent’s action. The reward, R, is expressed as:

The return is defined as the accumulated value of expected future rewards. Rewards from timesteps that are farther away in the future are less valuable than immediate rewards. Thus, the return is commonly calculated as the discounted return, G, defined as:

In this tutorial (and many other references), return refers to the discounted return. 

To compute the return:

• Start with the expected rewards from all future states.
• Multiply each future reward by an exponent of the discount factor, . For example, the expected reward after 2 timesteps (from the present) is multiplied by 2. 
• Sum all the discounted future rewards to calculate the return. 
• Normalize the value of the return. 

The function calculate_returns() performs these computations, as shown below:

def calculate_returns(rewards, discount_factor):
    returns = []
    cumulative_reward = 0
    for r in reversed(rewards):
        cumulative_reward = r + cumulative_reward * discount_factor
        returns.insert(0, cumulative_reward)
    returns = torch.tensor(returns)
    # normalize the return
    returns = (returns - returns.mean()) / returns.std()
    return returns

Implementing the advantage function

The advantage is calculated as the difference between the value predicted by the critic and the expected return from the actions chosen by the actor according to the policy. For a given action, the advantage expresses the benefit of taking that specific action over an arbitrary (average) action. 

In the original PPO paper (equation 10), the advantage, looking forward till timestep T is expressed as:

While coding the algorithm, the constraint of looking forward until a set number of timesteps is enforced via the batch size. So, the above equation can be simplified as the difference between the value and the expected returns. The expected returns are quantified in the state-action value function, Q. 

Thus, the simplified formula below expresses the advantage of choosing: 

• a particular action 
• in a given state 
• under a particular policy 
• at a particular timestep 

This is expressed as: 

OpenAI also uses this formula to implement RL. The calculate_advantages() function shown below calculates the advantage:

def calculate_advantages(returns, values):
    advantages = returns - values
    # Normalize the advantage
    advantages = (advantages - advantages.mean()) / advantages.std()
    return advantages

Surrogate loss and clipping mechanism

The policy loss would be the standard policy gradient loss without special techniques like PPO. The standard policy gradient loss is calculated as the product of:

• The policy action probabilities 
• The advantage function, which is calculated as the difference between:
• The policy return 
• The expected value

The standard policy gradient loss cannot make corrections for abrupt policy changes. The surrogate loss modifies the standard loss to restrict the amount the policy can change in each iteration. It is the minimum of two quantities:

• The product of:
• The policy ratio. This ratio expresses the difference between the old and new action probabilities.  
• The advantage function 
• The product of:
• The clamped value of the policy ratio. This ratio is clipped such that the updated policy is within a certain percentage of the old policy. 
• The advantage function 

For the optimization process, the surrogate loss is used as a proxy for the actual loss. 

The clipping mechanism

The policy ratio, R, is the difference between the new and old policies and is given as the ratio of the log probabilities of the policy under the new and old parameters:

The clipped policy ratio, R', is constrained such that: 

Given the advantage, At, as shown in the previous section, and the policy ratio, as shown above, the surrogate loss is calculated as:

The code below shows how to implement the clipping mechanism and the surrogate loss. 

def calculate_surrogate_loss(
        actions_log_probability_old,
        actions_log_probability_new,
        epsilon,
        advantages):
    advantages = advantages.detach()
    policy_ratio = (
            actions_log_probability_new - actions_log_probability_old
            ).exp()
    surrogate_loss_1 = policy_ratio * advantages
    surrogate_loss_2 = torch.clamp(
            policy_ratio, min=1.0-epsilon, max=1.0+epsilon
            ) * advantages
    surrogate_loss = torch.min(surrogate_loss_1, surrogate_loss_2)
    return surrogate_loss

3. Training the Agent

Now, let’s train the agent.

Calculating policy and value loss 

We are now ready to calculate the policy and value losses: 

• The policy loss is the sum of the surrogate loss and the entropy bonus. 
• The value loss is based on the difference between the value predicted by the critic and the returns (cumulative reward) generated by the policy. The value loss computation uses the Smooth L1 Loss function. This helps to smoothen the loss function and makes it less sensitive to outliers. 

Both the losses, as computed above, are tensors. Gradient descent is based on scalar values. To get a single scalar value representing the loss, use the .sum() function to sum the tensor elements. The function below shows how to do this: 

def calculate_losses(
        surrogate_loss, entropy, entropy_coefficient, returns, value_pred):
    entropy_bonus = entropy_coefficient * entropy
    policy_loss = -(surrogate_loss + entropy_bonus).sum()
    value_loss = f.smooth_l1_loss(returns, value_pred).sum()
    return policy_loss, value_loss

Defining the training loop

Before starting the training process, create a set of buffers as empty arrays. The training algorithm will use these buffers to store information about the agent’s actions, the environment’s states, and the rewards in each time step. The function below initializes these buffers: 

def init_training():
    states = []
    actions = []
    actions_log_probability = []
    values = []
    rewards = []
    done = False
    episode_reward = 0
    return states, actions, actions_log_probability, values, rewards, done, episode_reward

Each training iteration runs the agent with the policy parameters for that iteration. The agent interacts with the environment in timesteps in a loop until it reaches a terminal condition. 

After each timestep, the agent’s action, reward, and value are appended to the respective buffers. When the episode terminates, the function returns the updated set of buffers, which summarize the episode's results. 

Before running the training loop:

• Set the model to training mode using agent.train(). 
• Reset the environment to a random state using env.reset(). This is the starting state for this training iteration. 

The following steps explain what happens in each timestep in the training loop: 

• Pass the state to the agent. 
• The agent returns:
• The predicted action given the state, based on the policy (actor). Pass this predicted action tensor through the softmax function to get the set of action probabilities.  
• The predicted value of the state, based on the critic.
• The agent selects the action to take:
• Use the action probabilities to estimate the probability distribution. 
• Randomly select an action by picking a sample from this distribution. The dist.sample() function does this. 
• Use the env.step() function to pass this action to the environment to simulate the environment’s response for this timestep. Based on the agent’s action, the environment generates:
• The new state
• The reward
• The boolean return value done (this indicates whether the environment has reached a terminal state)
• Append to the respective buffers the values of the agent’s action, the rewards, the predicted values, and the new state. 

The training episode terminates when the env.step() function returns true for the boolean return value of done. 

After the episode has terminated, use the accumulated values from each timestep to calculate the cumulative returns from this episode by adding the rewards from each timestep. We use the calculate_returns() function described earlier to do this. This function’s inputs are the discount factor and the buffer containing the rewards from each timestep. We use these returns and the accumulated values from each timestep to calculate the advantages using the calculate_advantages() function. 

The following Python function shows how to implement these steps:

def forward_pass(env, agent, optimizer, discount_factor):
    states, actions, actions_log_probability, values, rewards, done, episode_reward = init_training()
    state = env.reset()
    agent.train()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        states.append(state)
        action_pred, value_pred = agent(state)
        action_prob = f.softmax(action_pred, dim=-1)
        dist = distributions.Categorical(action_prob)
        action = dist.sample()
        log_prob_action = dist.log_prob(action)
        state, reward, done, _ = env.step(action.item())
        actions.append(action)
        actions_log_probability.append(log_prob_action)
        values.append(value_pred)
        rewards.append(reward)
        episode_reward += reward
    states = torch.cat(states)
    actions = torch.cat(actions)
    actions_log_probability = torch.cat(actions_log_probability)
    values = torch.cat(values).squeeze(-1)
    returns = calculate_returns(rewards, discount_factor)
    advantages = calculate_advantages(returns, values)
    return episode_reward, states, actions, actions_log_probability, advantages, returns

Updating the model parameters

Each training iteration runs the model through a complete episode consisting of many timesteps (until it reaches a terminal condition). In each timestep, we store the policy parameters, the agent’s action, the returns, and the advantages. After each iteration, we update the model based on the policy’s performance through all the timesteps in that iteration. 

The maximum number of timesteps in the CartPole environment is 500. In more complex environments, there are more timesteps, even millions. In such cases, the training results dataset must be split into batches. The number of timesteps in each batch is called the optimization batch size. 

Thus, the steps to update the model parameters are:

• Split the training results dataset into batches. 
• For each batch:
• Get the agent’s action and the predicted value for each state.
• Use these predicted actions to estimate the new action probability distribution. 
• Use this distribution to calculate the entropy. 
• Use this distribution to get the log probability of the actions in the training results dataset. This is the new set of log probabilities of the actions in the training results dataset. The old set of log probabilities of these same actions was calculated in the training loop explained in the previous section. 
• Calculate the surrogate loss using the actions' old and new probability distributions. 
• Calculate the policy loss and the value loss using the surrogate loss, the entropy, and the advantages. 
• Run .backward() separately on the policy and value losses. This updates the gradients on the loss functions. 
• Run .step() on the optimizer to update the policy parameters. In this case, we use the Adam optimizer to balance speed and robustness. 
• Accumulate the policy and value losses. 
• Repeat the backward pass (the above operations) on each batch a few times, depending on the value of the parameter PPO_STEPS. Repeating the backward pass on each batch is computationally efficient because it effectively increases the size of the training dataset without having to run additional forward passes. The number of environment steps in each alternation between sampling and optimization is called the iteration batch size. 
• Return the average policy loss and value loss.

The code below implements these steps:

def update_policy(
        agent,
        states,
        actions,
        actions_log_probability_old,
        advantages,
        returns,
        optimizer,
        ppo_steps,
        epsilon,
        entropy_coefficient):
    BATCH_SIZE = 128
    total_policy_loss = 0
    total_value_loss = 0
    actions_log_probability_old = actions_log_probability_old.detach()
    actions = actions.detach()
    training_results_dataset = TensorDataset(
            states,
            actions,
            actions_log_probability_old,
            advantages,
            returns)
    batch_dataset = DataLoader(
            training_results_dataset,
            batch_size=BATCH_SIZE,
            shuffle=False)
    for _ in range(ppo_steps):
        for batch_idx, (states, actions, actions_log_probability_old, advantages, returns) in enumerate(batch_dataset):
            # get new log prob of actions for all input states
            action_pred, value_pred = agent(states)
            value_pred = value_pred.squeeze(-1)
            action_prob = f.softmax(action_pred, dim=-1)
            probability_distribution_new = distributions.Categorical(
                    action_prob)
            entropy = probability_distribution_new.entropy()
            # estimate new log probabilities using old actions
            actions_log_probability_new = probability_distribution_new.log_prob(actions)
            surrogate_loss = calculate_surrogate_loss(
                    actions_log_probability_old,
                    actions_log_probability_new,
                    epsilon,
                    advantages)
            policy_loss, value_loss = calculate_losses(
                    surrogate_loss,
                    entropy,
                    entropy_coefficient,
                    returns,
                    value_pred)
            optimizer.zero_grad()
            policy_loss.backward()
            value_loss.backward()
            optimizer.step()
            total_policy_loss += policy_loss.item()
            total_value_loss += value_loss.item()
    return total_policy_loss / ppo_steps, total_value_loss / ppo_steps

4. Running the PPO Agent 

Let’s finally run the PPO agent.

Evaluating the performance 

To evaluate the agent’s performance, create a fresh environment and calculate the cumulative rewards from running the agent in this new environment. You need to set the agent to evaluate mode using the .eval() function. The steps are the same as for the training loop. The code snippet below implements the evaluation function: 

def evaluate(env, agent):
    agent.eval()
    rewards = []
    done = False
    episode_reward = 0
    state = env.reset()
    while not done:
        state = torch.FloatTensor(state).unsqueeze(0)
        with torch.no_grad():
            action_pred, _ = agent(state)
            action_prob = f.softmax(action_pred, dim=-1)
        action = torch.argmax(action_prob, dim=-1)
        state, reward, done, _ = env.step(action.item())
        episode_reward += reward
    return episode_reward

Visualizing training results

We will use the Matplotlib library to visualize the progress of the training process. The function below shows how to plot the rewards from both the training and the testing loops:

def plot_train_rewards(train_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(train_rewards, label='Training Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Training Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(train_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

def plot_test_rewards(test_rewards, reward_threshold):
    plt.figure(figsize=(12, 8))
    plt.plot(test_rewards, label='Testing Reward')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Testing Reward', fontsize=20)
    plt.hlines(reward_threshold, 0, len(test_rewards), color='y')
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

In the example plots below, we show the training and testing rewards, obtained by applying the policy in the training and testing environments respectively. Note that the shape of these plots will appear different every time you run the code. This is because of the randomness inherent to the training process. 

Training rewards (obtained by applying the policy in the training environment). Image by Author.

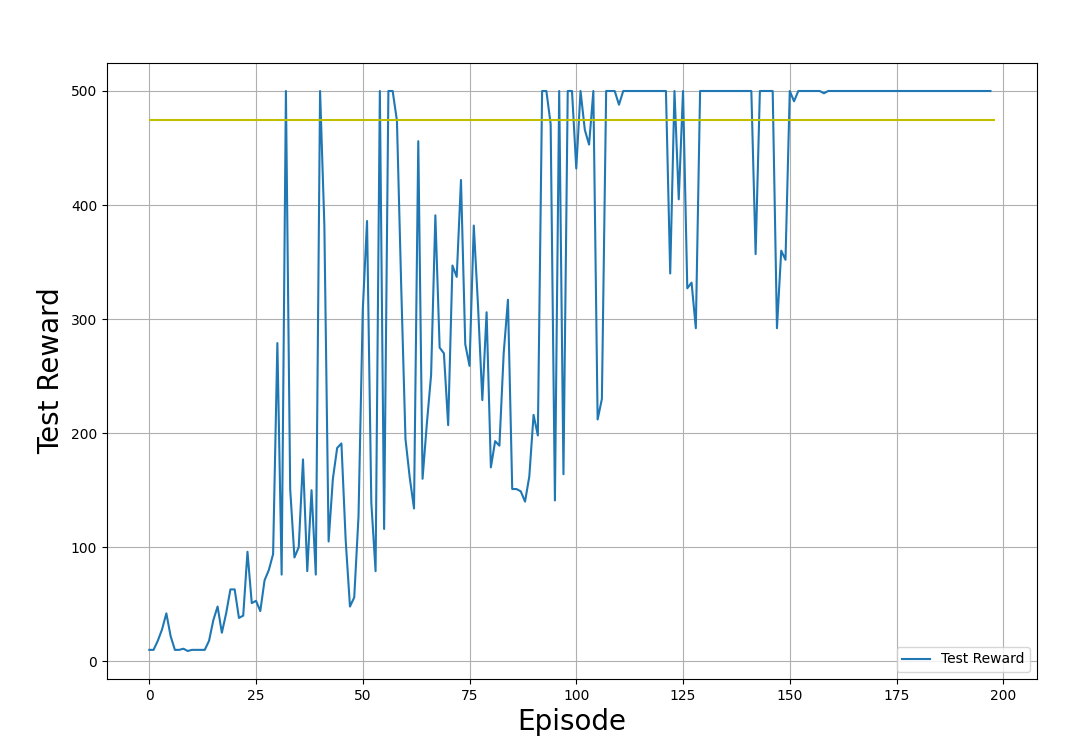
Testing rewards (obtained by applying the policy in the test environment). Image by Author. 

In the output graphs shown above, observe the progress of the training process:

• The reward starts from low values. As the training progresses, the rewards increase. 
• The rewards fluctuate randomly while increasing. This is due to the agent exploring the policy space. 
• The training terminates, and the testing rewards have stabilized around the threshold (475) for many iterations. 
• The rewards are capped at 500. These are constraints imposed by the environment (Gym CartPole v1). 

Similarly, you can plot the value and policy losses through the iterations:

def plot_losses(policy_losses, value_losses):
    plt.figure(figsize=(12, 8))
    plt.plot(value_losses, label='Value Losses')
    plt.plot(policy_losses, label='Policy Losses')
    plt.xlabel('Episode', fontsize=20)
    plt.ylabel('Loss', fontsize=20)
    plt.legend(loc='lower right')
    plt.grid()
    plt.show()

The example plot below shows the losses tracked through the training episodes:

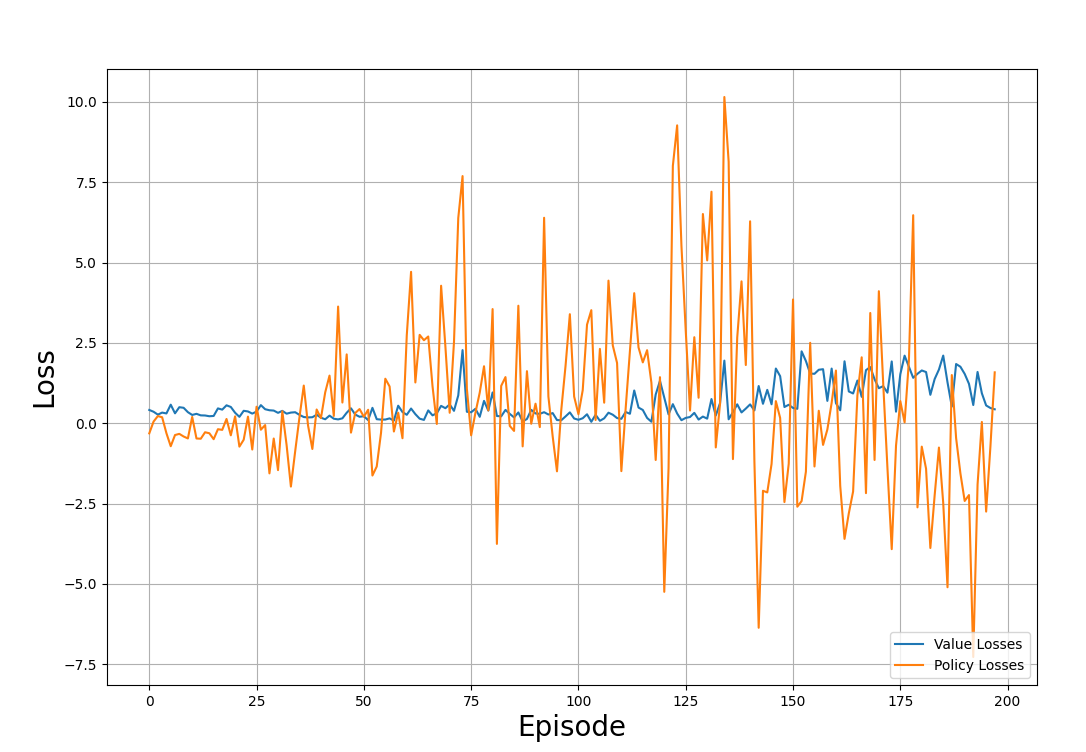
Value and policy losses through the training process. Image by Author

Observe the plot and notice:

• The losses appear to be randomly distributed and do not follow any pattern. 
• This is typical of RL training, where the goal is not to minimize the loss but to maximize the rewards. 

Run the PPO algorithm

You now have all the components to train the agent using PPO. To put it all together, you need to:

• Declare hyperparameters like discount factor, batch size, learning rate, etc. 
• Instantiate buffers as null arrays to store the rewards and losses from each iteration. 
• Create an agent instance using the create_agent() function.
• Iteratively run forward and backward passes using the forward_pass() and the update_policy() functions. 
• Test the policy’s performance using the evaluate() function. 
• Append the policy, value losses, and rewards from the training and evaluation functions to the respective buffers. 
• Compute the average of the rewards and losses over the last few timesteps. The example below averages the rewards and losses over the last 40 time steps. 
• Print the results of the evaluation every few steps. The example below prints every 10 steps. 
• Terminate the process when the average reward crosses a certain threshold. 

The code below shows how to declare a function which does this in Python:

def run_ppo():
    MAX_EPISODES = 500
    DISCOUNT_FACTOR = 0.99
    REWARD_THRESHOLD = 475
    PRINT_INTERVAL = 10
    PPO_STEPS = 8
    N_TRIALS = 100
    EPSILON = 0.2
    ENTROPY_COEFFICIENT = 0.01
    HIDDEN_DIMENSIONS = 64
    DROPOUT = 0.2
    LEARNING_RATE = 0.001
    train_rewards = []
    test_rewards = []
    policy_losses = []
    value_losses = []
    agent = create_agent(HIDDEN_DIMENSIONS, DROPOUT)
    optimizer = optim.Adam(agent.parameters(), lr=LEARNING_RATE)
    for episode in range(1, MAX_EPISODES+1):
        train_reward, states, actions, actions_log_probability, advantages, returns = forward_pass(
                env_train,
                agent,
                optimizer,
                DISCOUNT_FACTOR)
        policy_loss, value_loss = update_policy(
                agent,
                states,
                actions,
                actions_log_probability,
                advantages,
                returns,
                optimizer,
                PPO_STEPS,
                EPSILON,
                ENTROPY_COEFFICIENT)
        test_reward = evaluate(env_test, agent)
        policy_losses.append(policy_loss)
        value_losses.append(value_loss)
        train_rewards.append(train_reward)
        test_rewards.append(test_reward)
        mean_train_rewards = np.mean(train_rewards[-N_TRIALS:])
        mean_test_rewards = np.mean(test_rewards[-N_TRIALS:])
        mean_abs_policy_loss = np.mean(np.abs(policy_losses[-N_TRIALS:]))
        mean_abs_value_loss = np.mean(np.abs(value_losses[-N_TRIALS:]))
        if episode % PRINT_INTERVAL == 0:
            print(f'Episode: {episode:3} | \
                  Mean Train Rewards: {mean_train_rewards:3.1f} \
                  | Mean Test Rewards: {mean_test_rewards:3.1f} \
                  | Mean Abs Policy Loss: {mean_abs_policy_loss:2.2f} \
                  | Mean Abs Value Loss: {mean_abs_value_loss:2.2f}')
        if mean_test_rewards >= REWARD_THRESHOLD:
            print(f'Reached reward threshold in {episode} episodes')
            break
    plot_train_rewards(train_rewards, REWARD_THRESHOLD)
    plot_test_rewards(test_rewards, REWARD_THRESHOLD)
    plot_losses(policy_losses, value_losses)

Run the program: 

run_ppo()

The output should resemble the sample below: 

Episode:  10 | Mean Train Rewards: 22.3 | Mean Test Rewards: 30.4 | Mean Abs Policy Loss: 0.37 | Mean Abs Value Loss: 0.39 
Episode:  20 | Mean Train Rewards: 38.6 | Mean Test Rewards: 69.8 | Mean Abs Policy Loss: 0.46 | Mean Abs Value Loss: 0.37 
.
.
.
Episode: 100 | Mean Train Rewards: 289.5 | Mean Test Rewards: 427.3 | Mean Abs Policy Loss: 1.73 | Mean Abs Value Loss: 0.21 
Episode: 110 | Mean Train Rewards: 357.7 | Mean Test Rewards: 461.4 | Mean Abs Policy Loss: 1.86 | Mean Abs Value Loss: 0.22 
Reached reward threshold in 116 episodes

You can view and run the working program on this DataLab notebook!

5. Hyperparameter Tuning and Optimization

In machine learning, hyperparameters control the training process. Below, I explain some of the important hyperparameters used in PPO: 

• Learning rate: The learning rate decides how much policy parameters can vary in each iteration. In stochastic gradient descent, the amount by which the policy parameters are updated in each iteration is decided by the product of the learning rate and the gradient. 
• Clipping parameter: This is also referred to as epsilon, ε. It decides the extent to which the policy ratio is clipped. The ratio of the new and old policies is allowed to vary in the range [1-ε, 1+ε]. When it is beyond this range, it is artificially clipped to lie within the range. 
• Batch size: This refers to the number of steps to consider for each gradient update. In PPO, the batch size is the number of time steps needed to apply the policy and calculate the surrogate loss to update the policy parameters. In this article, we used a batch size of 64. 
• Iteration steps: This is the number of times each batch is re-used to run the backward pass. The code in this article refers to this as PPO_STEPS. In complex environments, running the forward pass many times is computationally expensive. A more efficient alternative is to re-run each batch a few times. It is typically recommended to use a value between 5 and 10. 
• Discount factor: This is also referred to as gamma, γ. It expresses the extent to which immediate rewards are more valuable than future rewards. This is similar to the concept of interest rates in calculating the time value of money. When is closer to 0, it means future rewards are less valuable and the agent should prioritize immediate rewards. When is closer to 1, it means future rewards are important. 
• Entropy coefficient: The entropy coefficient decides the entropy bonus, which is calculated as the product of the entropy coefficient and the entropy of the distribution. The role of the entropy bonus is to introduce more randomness into the policy. This encourages the agent to explore the policy space. However, the training fails to converge to an optimal policy when this randomness is too high. 
• Success criteria for the training: You need to set the criteria for deciding when the training is successful. A common way to do this is to put a condition that the average rewards over the last N trials (episodes) are above a certain threshold. In the example code above, this is expressed with the variable N_TRIALS. When this is set to a higher value, the training takes longer because the policy has to achieve the threshold reward over more episodes. It also results in a more robust policy while being computationally more expensive. Note that PPO is a stochastic policy, and there will be episodes when the agent doesn’t cross the threshold. So, if the value of N_TRIALS is too high, your training may not terminate.

Strategies for optimizing PPO performance

Optimizing the performance of training PPO algorithms involves trial and error and experimenting with different hyperparameter values. However, there are some broad guidelines: 

• Discount factor: When long-term rewards are important, as in the CartPole environment, where the pole needs to stay stable over time, start with a moderate gamma value, such as 0.99. 
• Entropy bonus: In complex environments, the agent must explore the action space to find the optimal policy. The entropy bonus promotes exploration. The entropy bonus is added to the surrogate loss. Check the magnitude of the surrogate loss and the distribution’s entropy before deciding the entropy coefficient. In this article, we used an entropy coefficient of 0.01.
• Clipping parameter: The clipping parameter decides how different the updated policy can be from the current policy. A large value of the clipping parameter encourages better exploration of the environment, but it risks destabilizing the training. You want a clipping parameter that allows gradual exploration while preventing destabilizing updates. In this article, we used a clipping parameter of 0.2.
• Learning rate: When the learning rate is too high, the policy is updated in large steps, and every iteration and the training process might become unstable. When it is too low, the training takes too long.  This tutorial used a learning rate of 0.001, which works well for the environment. In many cases, it is recommended to use a learning rate of 1e-5. 

Challenges and Best Practices in PPO

After explaining PPO's concepts and implementation details, let’s discuss the challenges and best practices. 

Common challenges in training PPO

Even though PPO is widely used, you need to be aware of potential challenges to solve real-world problems using this technique successfully. Some such challenges are:

• Slow convergence: In complex environments, PPO can be sample-inefficient and needs many interactions with the environment to converge on the optimal policy. This makes it slow and expensive to train. 
• Sensitivity to hyperparameters: PPO relies on efficiently exploring the policy space. The stability of the training process and the speed of convergence are sensitive to the values of the hyperparameters. The optimal values of these hyperparameters can often be determined only by trial and error. 
• Overfitting:  RL environments are typically initialized with random parameters. PPO training is based on finding the optimal policy based on the agent's environment. Sometimes, the training process converges to a set of optimal parameters for one specific environment but not for any randomized environment. This is typically addressed by having many iterations, each with a differently randomized training environment. 
• Dynamic environments: Simple RL environments, such as the CartPole environment, are static - the rules are the same through time. Many other environments, such as a robot learning to walk on an unstable moving surface, are dynamic - the rules of the environment change with time. To perform well in such environments, PPO often needs additional finetuning. 
• Exploration vs exploitation: The clipping mechanism of PPO ensures that policy updates are within a trusted region. However, it also prevents the agent from exploring the action space. This can lead to convergence to local optima, particularly in complex environments. On the other hand, allowing the agent to explore too much can prevent it from converging onto any optimum policy. 

Best practices for training PPO models

To get good results using PPO, I recommend some best practices, such as:

• Normalize input features: Normalizing the values of returns and advantages reduces the variability in data and leads to stable gradient updates. Normalizing the data brings all the values to a consistent numerical range. It helps reduce the effect of outliers and extreme values, which could otherwise distort the gradient updates and slow down convergence. 
• Use suitably large batch sizes: Small batches allow faster updates and training but can lead to convergence to local optima and instability in the training process. Larger batch sizes allow the agent to learn robust policies, leading to a stable training process. However, batch sizes that are too large are also suboptimal. In addition to increasing computational costs, they make policy updates less responsive to the value function because the gradient updates are based on averages estimated over large batches. Furthermore, it can lead to overfitting the updates to that specific batch. 
• Iteration steps: It is generally advisable to reuse each batch for 5-10 iterations. This makes the training process more efficient. Reusing the same batch too many times leads to overfitting. The code refers to this hyperparameter as PPO_STEPS. 
• Perform regular evaluation: To detect overfitting, it is essential to periodically monitor the policy's effectiveness. If the policy turns out to be ineffective in certain scenarios, further training or fine-tuning might be necessary. 
• Tune the hyperparameters: As explained earlier, PPO training is sensitive to the hyperparameters' values. Experiment with various hyperparameter values to determine the right set of values for your specific problem. 
• Shared backbone network: As illustrated in this article, using a shared backbone prevents imbalances between the actor and critic networks. Sharing a backbone network between the actor and critic helps with shared feature extraction and a common understanding of the environment. This makes the learning process more efficient and stable. It also helps reduce the computational space and time complexity of the algorithm. 
• Number and size of hidden layers: Increase the number of hidden layers and dimensions for more complex environments. Simpler problems like CartPole can be solved with a single hidden layer. The hidden layer used in this article has 64 dimensions. Making the network much larger than necessary is computationally wasteful and can make it unstable. 
• Early stopping: Stopping the training when the evaluation metrics are met helps prevent overtraining and avoids resource wastage. A common evaluation metric is when the agent exceeds the threshold rewards over the past N events. 

Conclusion

In this article, we discussed PPO as a way to solve RL problems. We then detailed the steps to implement PPO using PyTorch. Lastly, we presented some performance tips and best practices for PPO. 

The best way to learn is to implement the code yourself. You can also modify the code to work with other classic control environments in Gym. To learn how to implement RL agents using Python and OpenAI’s Gymnasium, follow the course Reinforcement Learning with Gymnasium in Python!