La función sigmoidea: Un componente clave en la ciencia de datos

La función sigmoidea es un concepto importante en la ciencia de datos y el machine learning, que potencia algoritmos como la regresión logística y las redes neuronales. Ayuda a convertir datos numéricos complicados en probabilidades más fáciles de interpretar. O, más exactamente, diría que transforma una entrada de valor real (en realidad, suele ser el resultado de un modelo lineal) en una salida de tipo probabilístico entre 0 y 1.

La sigmoide es, por tanto, esencial para tareas como la predicción de resultados binarios (decisiones sí/no o verdadero/falso) y la realización de predicciones informadas en modelos de machine learning de clasificación . En el resto de este tutorial te explicaré sus propiedades matemáticas, sus aplicaciones y también algunas de sus limitaciones.

¿Qué es la función sigmoidea?

En esencia, la función sigmoidea es una ecuación matemática que asigna cualquier número de valor real a un valor entre 0 y 1, lo que la hace ideal para resultados probabilísticos. Su fórmula es la siguiente 

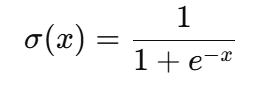
Dónde:

• x es la entrada de la función.
• e es la base del logaritmo natural (aproximadamente 2,718). 

La función sigmoidea se utiliza ampliamente en la ciencia de datos de dos formas principales:

• Clasificación binaria: La función sigmoide transforma el resultado de un modelo en una puntuación de probabilidad, que puede utilizarse para tareas como predecir impagos de préstamos, detectar fraudes o identificar correos basura.
• Función de activación: En las redes neuronales, la función sigmoidea añade no linealidad, lo que permite al modelo aprender patrones complejos en los datos.

Propiedades matemáticas de la función sigmoidea

La función sigmoidea presenta varias propiedades matemáticas que la convierten en una elección popular para diversas aplicaciones. 

Propiedades clave

• Alcance: Los valores de salida de la función sigmoidea siempre caen entre 0 y 1, por eso funciona bien para estimar probabilidades en tareas como la clasificación binaria.
• Monotonicidad: La función es monotónicamente creciente, lo que significa que a medida que aumenta el valor de entrada, el valor de salida también aumenta, pero nunca disminuye. Esta coherencia es útil a la hora de modelizar relaciones entre variables.
• Diferenciabilidad: La función sigmoidea es totalmente diferenciable, lo que significa que puedes calcular su derivada en cualquier punto. Esta propiedad es fundamental para técnicas de optimización como la retropropagación, que se utiliza para entrenar redes neuronales. 
• No linealidad: La función sigmoidea introduce la no linealidad, lo que permite a los modelos aprender patrones y límites de decisión más complejos. Esto es esencial para tareas en las que las relaciones lineales simples no son suficientes.

Visualización de la función sigmoidea

La característica curva en forma de S de la función sigmoidea es su rasgo más reconocible. Esta curva muestra cómo se aplastan los valores de entrada en el intervalo de 0 a 1.

He aquí una sencilla visualización:

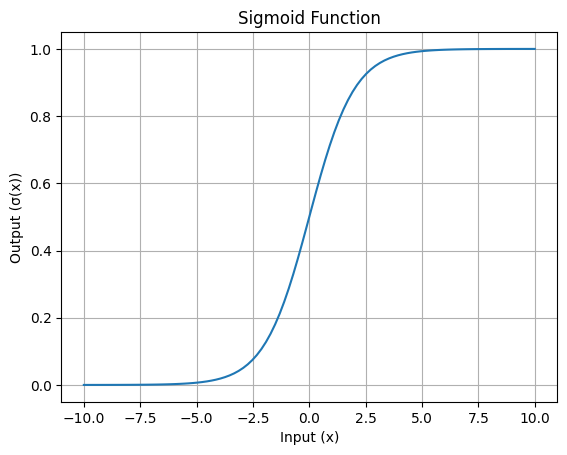
Curva en forma de S de la función Sigmoidea: Imagen del autor

El papel de la sigmoidea en la regresión logística

En regresión logísticase utiliza la función sigmoidea para convertir la combinación lineal de características de entrada en una puntuación de probabilidad:

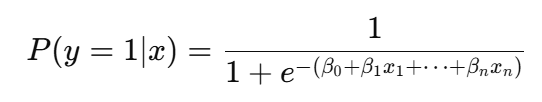
Más concretamente, la función sigmoidea se utiliza para modelar resultados binarios, lo que significa que ayuda a predecir si algo pertenece a una de dos categorías, como "sí" o "no", "por defecto" o "sin defecto", "spam" o "no spam".

La función toma el resultado de una combinación lineal de características de entrada y lo transforma en un valor de probabilidad entre 0 y 1. Esta probabilidad representa la probabilidad de que la entrada pertenezca a una clase determinada.

Por ejemplo, si la salida de la ecuación lineal es dos, la función sigmoidea lo convertirá en una probabilidad (por ejemplo, 0,88), que indica un 88% de posibilidades de que la entrada pertenezca a la clase positiva. Supongamos que el umbral se fija en 0,5, lo que determina la clasificación. Ahora bien, si el valor de la probabilidad es superior a 0,5, el modelo predice la clase positiva; en caso contrario, predice la clase negativa.

¿Por qué es necesaria esta transformación en primer lugar? Esto es necesario porque los resultados brutos del modelo lineal no son directamente interpretables como probabilidades. Al utilizar la función sigmoidea, la regresión logística no sólo proporciona clasificaciones, sino que también ofrece una clara comprensión probabilística, lo que resulta especialmente útil en aplicaciones como la predicción del riesgo, la clasificación del churn o la detección del fraude. Esta interpretación probabilística permite a los responsables establecer umbrales personalizados en función de las necesidades específicas de una tarea.

Aplicaciones en Redes Neuronales

La función sigmoidea desempeña un papel fundamental en las redes neuronales como función de activación.

Función de activación papel

El papel principal de la función sigmoidea como función de activación es tomar la suma ponderada de las entradas de la capa anterior y transformarla en un valor de salida entre 0 y 1. Esta transformación es útil para introducir la no linealidad en el modelo, lo que permite a las capas ocultas de una red neuronal profunda aprender relaciones complejas y resolver problemas que no pueden separarse con líneas rectas, como el reconocimiento de imágenes o el procesamiento del lenguaje natural.

Problema del gradiente de fuga

Sin embargo, la función sigmoidea tiene limitaciones, siendo la principal el problema del gradiente evanescente. Para valores de entrada muy grandes o muy pequeños, la salida de la función satura cerca de 1 o 0, y su gradiente se vuelve casi cero. Esto provoca la ralentización del proceso de aprendizaje en las redes neuronales densas, porque ahora los pesos se actualizan con demasiada lentitud durante el entrenamiento.

Funciones de activación alternativas

Para hacer frente a esta limitación, se suelen utilizar otras funciones de activación como ReLU (Unidad Lineal Rectificada) y Tanh. ReLU es computacionalmente más sencillo y evita el problema del gradiente evanescente para entradas positivas. Tanh, al igual que sigmoide, tiene forma de S, pero emite valores entre -1 y 1, lo que la hace centrada en cero y más eficiente en determinados escenarios. Estas alternativas han sustituido en gran medida a la sigmoidea en las redes profundas, excepto en las capas de salida para tareas como la clasificación binaria.

Consideraciones clave y limitaciones

Aunque la función sigmoidea tiene muchas ventajas, presenta algunos problemas que pueden afectar a su rendimiento en determinadas situaciones. 

Problema de saturación

La función sigmoidea puede saturarse cuando los valores de entrada son demasiado grandes (positivos) o demasiado pequeños (negativos). Saturación significa que la salida se acerca mucho a 0 ó 1, y el gradiente (tasa de cambio) se vuelve casi cero. 

Esto es problemático porque cuando el gradiente está cerca de cero, el modelo tiene dificultades para aprender durante el entrenamiento. En consecuencia, esto ralentiza las actualizaciones en los métodos de optimización basados en el gradiente, como la retropropagación.

Salida centrada en cero

Otra limitación de la función sigmoidea es que su salida está comprendida entre 0 y 1, y no está centrada en cero. Esto significa que todas las salidas son positivas, lo que puede alterar la distribución de las entradas en una red neuronal y hacer que la optimización sea más lenta. En cambio, funciones como Tanh tienen salidas que van de -1 a 1, lo que ayuda a mantener la media de las activaciones más cercana a cero y esto acelera la convergencia.

Coste computacional

La función sigmoidea se basa en la operación exponencial, que es computacionalmente cara en comparación con funciones de activación más sencillas como la ReLU (Unidad Lineal Rectificada). Por ejemplo, la fórmula sigmoidea es:

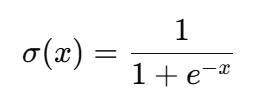
En este caso, el cálculo exponencial es más intensivo computacionalmente que las operaciones en ReLU, que sólo implican comparaciones y funciones lineales, y se da como:

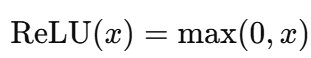
Para las redes neuronales modernas, especialmente las que tienen muchas capas y neuronas, el coste de realizar repetidamente la operación exponencial se acumula, y ahí es donde se emplean las alternativas.

Conclusión

La función sigmoidea es una herramienta importante en la ciencia de datos, especialmente para tareas como la regresión logística y como función de activación en redes neuronales. Ayuda a transformar las entradas en probabilidades e introduce la no linealidad en los modelos, haciéndolos capaces de manejar patrones complejos. Sin embargo, tiene problemas, como la saturación, la falta de salidas centradas en cero y unos costes computacionales más elevados, que pueden afectar a su eficacia en las redes profundas.

Aunque las técnicas modernas han introducido alternativas, no se puede exagerar la importancia de la función sigmoidea en la configuración de las metodologías de la ciencia de datos. Si quieres profundizar en su funcionamiento y verlo en acción, considera la posibilidad de explorar nuestros cursos interactivos y tutoriales sobre redes neuronales y regresión logística. Nuestra Introducción al Aprendizaje Profundo en Python es una gran opción.