La fonction sigmoïde : Un élément clé de la science des données

La fonction sigmoïde est un concept important de la science des données et de l'apprentissage automatique, qui alimente des algorithmes tels que la régression logistique et les réseaux neuronaux. Il permet de convertir des données numériques complexes en probabilités plus faciles à interpréter. Ou, plus précisément, je dirais qu'il transforme une entrée à valeur réelle (en réalité, il s'agit souvent du résultat d'un modèle linéaire) en une sortie de type probabilité entre 0 et 1.

La sigmoïde est donc essentielle pour des tâches telles que la prédiction de résultats binaires (décisions oui/non ou vrai/faux) et la réalisation de prédictions éclairées dans les modèles d'apprentissage automatique de la classification. Dans la suite de ce tutoriel, j'expliquerai ses propriétés mathématiques, ses applications et certaines de ses limites.

Qu'est-ce que la fonction sigmoïde ?

La fonction sigmoïde est une équation mathématique qui associe tout nombre réel à une valeur comprise entre 0 et 1, ce qui la rend idéale pour les résultats probabilistes. Sa formule est donnée ci-dessous : 

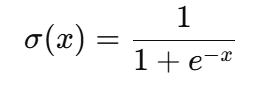
Où ?

• x est l'entrée de la fonction.
• e est la base du logarithme naturel (environ 2,718). 

La fonction sigmoïde est largement utilisée dans la science des données de deux manières principales :

• Classification binaire : La fonction sigmoïde transforme la sortie d'un modèle en un score de probabilité, qui peut ensuite être utilisé pour des tâches telles que la prédiction des défauts de paiement, la détection des fraudes ou l'identification des courriers électroniques non sollicités.
• Fonction d'activation : Dans les réseaux neuronaux, la fonction sigmoïde ajoute de la non-linéarité, ce qui permet au modèle d'apprendre des schémas complexes dans les données.

Propriétés mathématiques de la fonction sigmoïde

La fonction sigmoïde présente plusieurs propriétés mathématiques qui en font un choix populaire pour diverses applications. 

Propriétés principales

• Gamme : Les valeurs de sortie de la fonction sigmoïde se situent toujours entre 0 et 1, c'est pourquoi elle fonctionne bien pour estimer les probabilités dans des tâches telles que la classification binaire.
• Monotonicité : La fonction est monotone, c'est-à-dire que lorsque la valeur d'entrée augmente, la valeur de sortie augmente également, mais ne diminue jamais. Cette cohérence est utile pour modéliser les relations entre les variables.
• Différenciabilité : La fonction sigmoïde est entièrement différentiable, ce qui signifie que vous pouvez calculer sa dérivée en tout point. Cette propriété est essentielle pour les techniques d'optimisation telles que la rétropropagation, qui est utilisée pour former les réseaux neuronaux. 
• Non-linéarité : La fonction sigmoïde introduit la non-linéarité, ce qui permet aux modèles d'apprendre des modèles plus complexes et des limites de décision. Ceci est essentiel pour les tâches où les relations linéaires simples ne sont pas suffisantes.

Visualisation de la fonction sigmoïde

Lacourbecaractéristique en forme de S de la fonction sigmoïde est son trait le plus reconnaissable. Cette courbe montre comment les valeurs d'entrée sont écrasées dans la plage de 0 à 1.

Voici une visualisation simple :

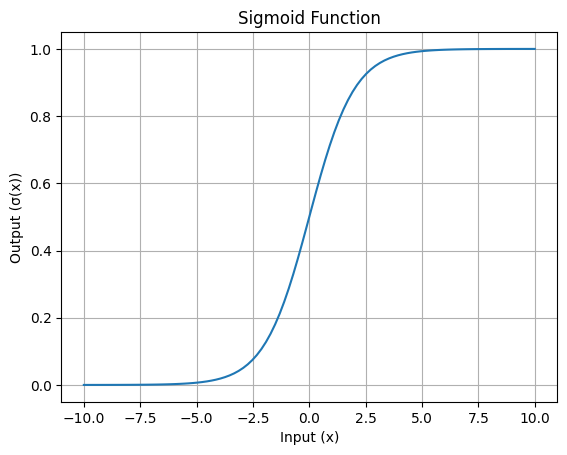
Courbe en S de la fonction sigmoïde : Image par l'auteur

Rôle de la sigmoïde dans la régression logistique

Dans le cadre d'une régression logistiquela fonction sigmoïde est utilisée pour convertir la combinaison linéaire des caractéristiques d'entrée en un score de probabilité :

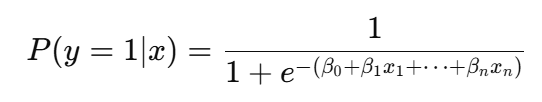
Plus précisément, la fonction sigmoïde est utilisée pour modéliser des résultats binaires, ce qui signifie qu'elle permet de prédire si un élément appartient à l'une des deux catégories suivantes : "oui" ou "non", "par défaut" ou "sans défaut", "spam" ou "non spam".

La fonction prend le résultat d'une combinaison linéaire des caractéristiques d'entrée et le transforme en une valeur de probabilité comprise entre 0 et 1. Cette probabilité représente la probabilité que l'entrée appartienne à une classe particulière.

Par exemple, si la sortie de l'équation linéaire est deux, la fonction sigmoïde la convertira en probabilité (par exemple, 0,88), ce qui indique qu'il y a 88 % de chances que l'entrée appartienne à la classe positive. Supposons que le seuil soit fixé à 0,5, ce qui détermine la classification. Maintenant, si la valeur de la probabilité est supérieure à 0,5, le modèle prédit la classe positive ; sinon, il prédit la classe négative.

Pourquoi cette transformation est-elle nécessaire ? Cela est nécessaire car les résultats bruts du modèle linéaire ne sont pas directement interprétables en tant que probabilités. En utilisant la fonction sigmoïde, la régression logistique ne fournit pas seulement des classifications mais aussi une compréhension probabiliste claire, ce qui est particulièrement utile dans des applications telles que la prédiction des risques, la classification du taux de désabonnement ou la détection des fraudes. Cette interprétation probabiliste permet aux décideurs de fixer des seuils personnalisés en fonction des besoins spécifiques d'une tâche.

Applications des réseaux neuronaux

La fonction sigmoïde joue un rôle central dans les réseaux neuronaux en tant que fonction d'activation.

Rôle de la fonction d'activation

Le rôle principal de la fonction sigmoïde en tant que fonction d'activation est de prendre la somme pondérée des entrées de la couche précédente et de la transformer en une valeur de sortie comprise entre 0 et 1. Cette transformation est utile pour introduire la non-linéarité dans le modèle, ce qui permet aux couches cachées d'un réseau neuronal profond d'apprendre des relations complexes et de résoudre des problèmes qui ne peuvent être séparés par des lignes droites, comme la reconnaissance d'images ou le traitement du langage naturel.

Problème du gradient de fuite

Cependant, la fonction sigmoïde présente des limites, la principale étant le problème du gradient de fuite. Pour des valeurs d'entrée très grandes ou très petites, la sortie de la fonction sature près de 1 ou de 0, et son gradient devient presque nul. Cela entraîne un ralentissement du processus d'apprentissage dans les réseaux neuronaux denses, car les poids sont mis à jour trop lentement au cours de la formation.

Autres fonctions d'activation

Pour remédier à cette limitation, d'autres fonctions d'activation telles que ReLU (Rectified Linear Unit) et Tanh sont souvent utilisées. La ReLU est plus simple sur le plan informatique et évite le problème de la disparition du gradient pour les entrées positives. Tanh, comme la sigmoïde, est en forme de S mais produit des valeurs entre -1 et 1, ce qui le rend centré sur le zéro et plus efficace dans certains scénarios. Ces alternatives ont largement remplacé la sigmoïde dans les réseaux profonds, sauf dans les couches de sortie pour des tâches telles que la classification binaire.

Principales considérations et limites

Si la fonction sigmoïde présente de nombreux avantages, elle n'est pas sans poser quelques problèmes qui peuvent avoir une incidence sur ses performances dans certaines situations. 

Problème de saturation

La fonction sigmoïde peut saturer lorsque les valeurs d'entrée sont trop grandes (positives) ou trop petites (négatives). La saturation signifie que la sortie est très proche de 0 ou de 1 et que le gradient (taux de variation) devient presque nul. 

Cette situation est problématique car lorsque le gradient est proche de zéro, le modèle a du mal à apprendre pendant la formation. Par conséquent, cela ralentit les mises à jour dans les méthodes d'optimisation basées sur le gradient, comme la rétropropagation.

Sortie centrée sur le zéro

Une autre limite de la fonction sigmoïde est que sa sortie se situe entre 0 et 1, et qu'elle n'est pas centrée sur le zéro. Cela signifie que toutes les sorties sont positives, ce qui peut modifier la distribution des entrées dans un réseau neuronal et ralentir l'optimisation. En revanche, des fonctions comme Tanh ont des sorties comprises entre -1 et 1, ce qui permet de maintenir la moyenne des activations plus proche de zéro et d'accélérer la convergence.

Coût de calcul

La fonction sigmoïde repose sur l'opération exponentielle, qui est coûteuse en termes de calcul par rapport à des fonctions d'activation plus simples telles que ReLU (Rectified Linear Unit). Par exemple, la formule sigmoïde est la suivante :

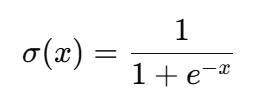
Dans ce cas, le calcul exponentiel est plus intensif que les opérations de ReLU, qui n'impliquent que des comparaisons et des fonctions linéaires, et est donné par la formule suivante :

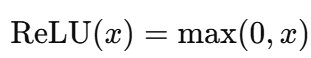
Pour les réseaux neuronaux modernes, en particulier ceux qui comportent de nombreuses couches et neurones, le coût de l'exécution répétée de l'opération exponentielle augmente, et c'est là que les alternatives sont employées.

Conclusion

La fonction sigmoïde est un outil important dans la science des données, en particulier pour des tâches telles que la régression logistique et comme fonction d'activation dans les réseaux neuronaux. Il permet de transformer les données d'entrée en probabilités et d'introduire la non-linéarité dans les modèles, ce qui les rend capables de traiter des modèles complexes. Cependant, elle présente des difficultés, telles que la saturation, l'absence de sorties centrées sur le zéro et des coûts de calcul plus élevés, qui peuvent affecter son efficacité dans les réseaux profonds.

Bien que les techniques modernes aient introduit des alternatives, l'importance de la fonction sigmoïde dans l'élaboration des méthodologies de la science des données ne peut être surestimée. Si vous souhaitez approfondir le fonctionnement des réseaux neuronaux et les voir à l'œuvre, vous pouvez explorer nos cours et tutoriels interactifs sur les réseaux neuronaux et la régression logistique. Notre introduction à l'apprentissage profond en Python est une excellente option.