The Sigmoid Function: A Key Component in Data Science

The sigmoid function is an important concept in data science and machine learning, powering algorithms such as logistic regression and neural networks. It helps convert complicated numerical data into probabilities that are easier to interpret. Or, more precisely, I would say it transforms a real-valued input (really, this is often the result of a linear model) into a probability-like output between 0 and 1.

The sigmoid is therefore essential for tasks like predicting binary outcomes (yes/no or true/false decisions) and making informed predictions in classification machine learning models. In the rest of this tutorial I will explain the mathematical properties, applications, and also some of its limitations.

What Is the Sigmoid Function?

At its core, the sigmoid function is a mathematical equation that maps any real-valued number to a value between 0 and 1, making it ideal for probabilistic outputs. Its formula is given below: 

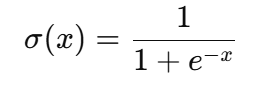
Where:

• x is the input to the function.
• e is the base of the natural logarithm (approximately 2.718). 

The sigmoid function is widely used in data science in two main ways:

• Binary classification: The sigmoid function transforms the output of a model into a probability score, which can then be used for tasks like predicting loan defaults, detecting fraud, or identifying spam emails.
• Activation function: In neural networks, the sigmoid function adds non-linearity, which allows the model to learn complex patterns in data.

Mathematical Properties of the Sigmoid Function

The sigmoid function exhibits several mathematical properties that make it a popular choice for various applications. 

Key properties

• Range: The output values of the sigmoid function always fall between 0 and 1, which is why it works well for estimating probabilities in tasks like binary classification.
• Monotonicity: The function is monotonically increasing, meaning as the input value increases, the output value also increases, but never decreases. This consistency is helpful when modeling relationships between variables.
• Differentiability: The sigmoid function is fully differentiable, which means you can calculate its derivative at any point. This property is critical for optimization techniques like backpropagation, which is used to train neural networks. 
• Non-linearity: The sigmoid function introduces non-linearity, allowing models to learn more complex patterns and decision boundaries. This is essential for tasks where simple linear relationships are not sufficient.

Visualizing the Sigmoid function

The characteristic S-shaped curve of the sigmoid function is its most recognizable feature. This curve shows how input values are squashed into the range of 0 to 1.

Here’s a simple visualization:

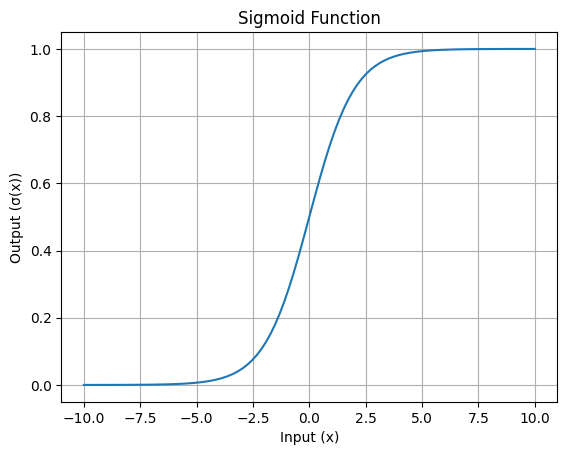
S-shaped curve of the Sigmoid function: Image by Author

Sigmoid's Role in Logistic Regression

In logistic regression, the sigmoid function is used to convert the linear combination of input features into a probability score:

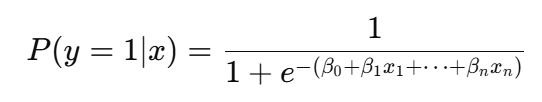
More specifically, the sigmoid function is used to model binary outcomes, meaning it helps predict whether something belongs to one of two categories, such as "yes" or "no," “default” or “no-default”,  "spam" or "not spam."

The function takes the result of a linear combination of input features and transforms it into a probability value between 0 and 1. This probability represents how likely it is that the input belongs to a particular class.

For example, if the output of the linear equation is two, the sigmoid function will convert this into a probability (e.g., 0.88), which indicates an 88% chance that the input belongs to the positive class. Suppose the threshold is set at 0.5, which determines the classification. Now, if the probability value is above 0.5, the model predicts the positive class; otherwise, it predicts the negative class.

Why is this transformation even required in the first place? This is required because raw outputs from the linear model aren't directly interpretable as probabilities. By using the sigmoid function, logistic regression not only provides classifications but also gives a clear probabilistic understanding, which is especially useful in applications like risk prediction, churn classification, or fraud detection. This probabilistic interpretation allows decision-makers to set custom thresholds based on the specific needs of a task.

Applications in Neural Networks

The sigmoid function plays a pivotal role in neural networks as an activation function.

Activation function role

The sigmoid function’s primary role as an activation function is to take the weighted sum of inputs from the previous layer and transform it into an output value between 0 and 1. This transformation is useful to introduce non-linearity into the model, which allows the hidden layers in a deep neural network to learn complex relationships and solve problems that cannot be separated with straight lines, such as image recognition or natural language processing.

Vanishing gradient problem

However, the sigmoid function has limitations, with the major one being that of the vanishing gradient problem. For very large or very small input values, the function's output saturates close to 1 or 0, and its gradient becomes nearly zero. This results in the slowing down of the learning process in dense neural networks because the weights are now getting updated too slowly during training.

Alternative activation functions

To address this limitation, other activation functions like ReLU (Rectified Linear Unit) and Tanh are often used. ReLU is computationally simpler and avoids the vanishing gradient problem for positive inputs. Tanh, like sigmoid, is S-shaped but outputs values between -1 and 1, which makes it zero-centered and more efficient in certain scenarios. These alternatives have largely replaced sigmoid in deep networks, except in the output layers for tasks like binary classification.

Key Considerations and Limitations

While the sigmoid function has many advantages, it does come with some challenges that can impact its performance in certain situations. 

Saturation issue

The sigmoid function can saturate when the input values are too large (positive) or too small (negative). Saturation means the output gets very close to 0 or 1, and the gradient (rate of change) becomes almost zero. 

This is problematic because when the gradient is near zero, the model struggles to learn during training. Consequently, this slows down the updates in gradient-based optimization methods like backpropagation.

Zero-centered output

Another limitation of the sigmoid function is that its output lies between 0 to 1, and it is not zero-centered. This means that all outputs are positive, which can shift the distribution of inputs in a neural network and make optimization slower. In contrast, functions like Tanh have outputs ranging from -1 to 1, which helps keep the mean of the activations closer to zero and this speeds up convergence.

Computational cost

The sigmoid function relies on the exponential operation, which is computationally expensive compared to simpler activation functions like ReLU (Rectified Linear Unit). For example, the sigmoid formula is:

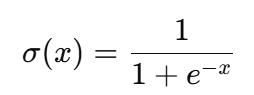
Here, the exponential calculation is more computationally intensive, than the operations in ReLU, which only involve comparisons and linear functions, and is given as:

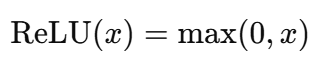
For modern neural networks, especially those with many layers and neurons, the cost of repeatedly performing the exponential operation adds up, and that’s where the alternatives are employed.

Conclusion

The sigmoid function is an important tool in data science, especially for tasks like logistic regression and as an activation function in neural networks. It helps transform inputs into probabilities and introduces non-linearity to models, making them capable of handling complex patterns. However, it does have challenges, such as saturation, lack of zero-centered outputs, and higher computational costs, which can affect its efficiency in deep networks.

While modern techniques have introduced alternatives, the sigmoid function’s importance in shaping data science methodologies cannot be overstated. If you want to dive deeper into how it works and see it in action, consider exploring our interactive courses and tutorials on neural networks and logistic regression. Our Introduction to Deep Learning in Python is one great option.