A função sigmoide: Um componente essencial da ciência de dados

A função sigmoide é um conceito importante na ciência de dados e no machine learning, alimentando algoritmos como regressão logística e redes neurais. Ele ajuda a converter dados numéricos complicados em probabilidades que são mais fáceis de interpretar. Ou, mais precisamente, eu diria que ele transforma uma entrada com valor real (na verdade, isso geralmente é o resultado de um modelo linear) em uma saída semelhante a uma probabilidade entre 0 e 1.

Portanto, a sigmoide é essencial para tarefas como a previsão de resultados binários (decisões do tipo sim/não ou verdadeiro/falso) e a realização de previsões informadas em modelos de machine learning de classificação . No restante deste tutorial, explicarei as propriedades matemáticas, os aplicativos e também algumas de suas limitações.

O que é a função sigmoide?

Em sua essência, a função sigmoide é uma equação matemática que mapeia qualquer número de valor real para um valor entre 0 e 1, o que a torna ideal para saídas probabilísticas. Sua fórmula é dada abaixo: 

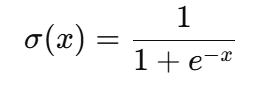
Onde:

• x é a entrada para a função.
• e é a base do logaritmo natural (aproximadamente 2,718). 

A função sigmoide é amplamente usada na ciência de dados de duas maneiras principais:

• Classificação binária: A função sigmoide transforma a saída de um modelo em uma pontuação de probabilidade, que pode ser usada para tarefas como prever inadimplência de empréstimos, detectar fraudes ou identificar e-mails de spam.
• Função de ativação: Nas redes neurais, a função sigmoide acrescenta não linearidade, o que permite que o modelo aprenda padrões complexos nos dados.

Propriedades matemáticas da função sigmoide

A função sigmoide apresenta várias propriedades matemáticas que a tornam uma escolha popular para várias aplicações. 

Principais propriedades

• Alcance: Os valores de saída da função sigmoide sempre ficam entre 0 e 1, e é por isso que ela funciona bem para estimar probabilidades em tarefas como classificação binária.
• Monotonicidade: A função é monotonicamente crescente, ou seja, à medida que o valor de entrada aumenta, o valor de saída também aumenta, mas nunca diminui. Essa consistência é útil ao modelar relações entre variáveis.
• Diferenciabilidade: A função sigmoide é totalmente diferenciável, o que significa que você pode calcular sua derivada em qualquer ponto. Essa propriedade é fundamental para técnicas de otimização como a retropropagação, que é usada para treinar redes neurais. 
• Não linearidade: A função sigmoide introduz a não linearidade, permitindo que os modelos aprendam padrões mais complexos e limites de decisão. Isso é essencial para tarefas em que as relações lineares simples não são suficientes.

Visualização da função sigmoide

A curvacaracterística em forma de S da função sigmoide é sua característica mais reconhecível. Essa curva mostra como os valores de entrada são esmagados no intervalo de 0 a 1.

Aqui está uma visualização simples:

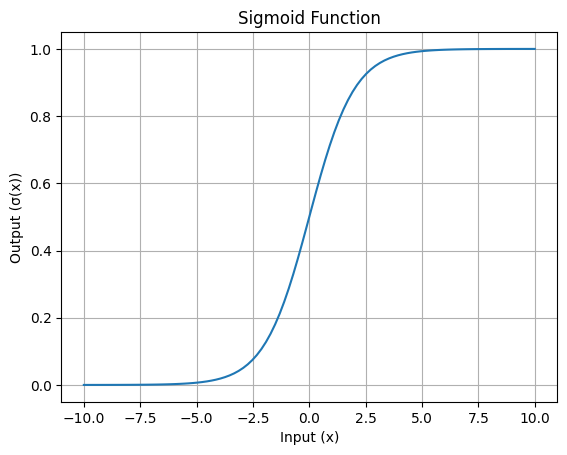
Curva em forma de S da função Sigmoid: Imagem do autor

O papel do Sigmoid na regressão logística

Em regressão logísticaa função sigmoide é usada para converter a combinação linear dos recursos de entrada em uma pontuação de probabilidade:

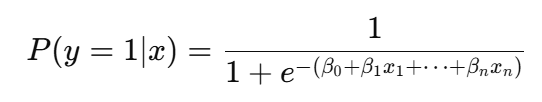
Mais especificamente, a função sigmoide é usada para modelar resultados binários, o que significa que ela ajuda a prever se algo pertence a uma de duas categorias, como "sim" ou "não", "padrão" ou "não padrão", "spam" ou "não spam".

A função pega o resultado de uma combinação linear de recursos de entrada e o transforma em um valor de probabilidade entre 0 e 1. Essa probabilidade representa a probabilidade de o input pertencer a uma determinada classe.

Por exemplo, se o resultado da equação linear for dois, a função sigmoide converterá isso em uma probabilidade (por exemplo, 0,88), o que indica uma chance de 88% de que a entrada pertença à classe positiva. Suponha que o limite seja definido como 0,5, o que determina a classificação. Agora, se o valor da probabilidade estiver acima de 0,5, o modelo prevê a classe positiva; caso contrário, ele prevê a classe negativa.

Em primeiro lugar, por que essa transformação é necessária? Isso é necessário porque os resultados brutos do modelo linear não podem ser interpretados diretamente como probabilidades. Com o uso da função sigmoide, a regressão logística não só fornece classificações, mas também uma compreensão probabilística clara, o que é especialmente útil em aplicativos como previsão de risco, classificação de rotatividade ou detecção de fraude. Essa interpretação probabilística permite que os tomadores de decisão definam limites personalizados com base nas necessidades específicas de uma tarefa.

Aplicações em redes neurais

A função sigmoide desempenha um papel fundamental nas redes neurais como uma função de ativação.

Papel da função de ativação

A função principal da função sigmoide como função de ativação é pegar a soma ponderada das entradas da camada anterior e transformá-la em um valor de saída entre 0 e 1. Essa transformação é útil para introduzir a não linearidade no modelo, o que permite que as camadas ocultas em uma rede neural profunda aprendam relações complexas e resolvam problemas que não podem ser separados por linhas retas, como o reconhecimento de imagens ou o processamento de linguagem natural.

Problema do gradiente de fuga

No entanto, a função sigmoide tem limitações, sendo a principal delas o problema do gradiente de desaparecimento. Para valores de entrada muito grandes ou muito pequenos, a saída da função satura perto de 1 ou 0, e seu gradiente se torna quase zero. Isso resulta na desaceleração do processo de aprendizagem em redes neurais densas porque os pesos estão sendo atualizados muito lentamente durante o treinamento.

Funções de ativação alternativas

Para resolver essa limitação, outras funções de ativação, como ReLU (Rectified Linear Unit) e Tanh, são usadas com frequência. O ReLU é computacionalmente mais simples e evita o problema do gradiente de desaparecimento para entradas positivas. O Tanh, assim como o sigmoide, tem formato de S, mas produz valores entre -1 e 1, o que o torna centrado em zero e mais eficiente em determinados cenários. Essas alternativas substituíram amplamente o sigmoide em redes profundas, exceto nas camadas de saída para tarefas como classificação binária.

Principais considerações e limitações

Embora a função sigmoide tenha muitas vantagens, ela apresenta alguns desafios que podem afetar seu desempenho em determinadas situações. 

Problema de saturação

A função sigmoide pode saturar quando os valores de entrada são muito grandes (positivos) ou muito pequenos (negativos). Saturação significa que a saída fica muito próxima de 0 ou 1, e o gradiente (taxa de alteração) torna-se quase zero. 

Isso é problemático porque, quando o gradiente está próximo de zero, o modelo tem dificuldade para aprender durante o treinamento. Consequentemente, isso torna as atualizações mais lentas nos métodos de otimização baseados em gradiente, como o backpropagation.

Saída centrada em zero

Outra limitação da função sigmoide é que sua saída está entre 0 e 1 e não é centrada no zero. Isso significa que todas as saídas são positivas, o que pode alterar a distribuição das entradas em uma rede neural e tornar a otimização mais lenta. Em contrapartida, funções como Tanh têm saídas que variam de -1 a 1, o que ajuda a manter a média das ativações mais próxima de zero, acelerando a convergência.

Custo computacional

A função sigmoide se baseia na operação exponencial, que é computacionalmente cara em comparação com funções de ativação mais simples, como a ReLU (Unidade Linear Retificada). Por exemplo, a fórmula sigmoide é:

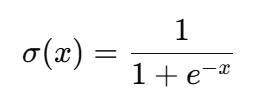
Aqui, o cálculo exponencial é mais intensivo em termos de computação do que as operações no ReLU, que envolvem apenas comparações e funções lineares, e é dado como:

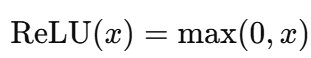
Para as redes neurais modernas, especialmente aquelas com muitas camadas e neurônios, o custo de executar repetidamente a operação exponencial aumenta, e é aí que as alternativas são empregadas.

Conclusão

A função sigmoide é uma ferramenta importante na ciência de dados, especialmente para tarefas como regressão logística e como função de ativação em redes neurais. Ele ajuda a transformar entradas em probabilidades e introduz a não linearidade nos modelos, tornando-os capazes de lidar com padrões complexos. No entanto, ele tem desafios, como saturação, falta de saídas centradas em zero e custos computacionais mais altos, o que pode afetar sua eficiência em redes profundas.

Embora as técnicas modernas tenham introduzido alternativas, a importância da função sigmoide na formação das metodologias de ciência de dados não pode ser exagerada. Se você quiser se aprofundar em como elas funcionam e vê-las em ação, considere explorar nossos cursos interativos e tutoriais sobre redes neurais e regressão logística. Em nossa Introdução à aprendizagem profunda em Python, você encontrará uma ótima opção.