Die Sigmoid-Funktion: Eine Schlüsselkomponente in der Datenwissenschaft

Die Sigmoidfunktion ist ein wichtiges Konzept in der Datenwissenschaft und im maschinellen Lernen, das Algorithmen wie die logistische Regression und neuronale Netze unterstützt. Sie hilft dabei, komplizierte numerische Daten in Wahrscheinlichkeiten umzuwandeln, die leichter zu interpretieren sind. Genauer gesagt würde ich sagen, es wandelt eine reellwertige Eingabe (in Wirklichkeit ist das oft das Ergebnis eines linearen Modells) in eine wahrscheinlichkeitsähnliche Ausgabe zwischen 0 und 1 um.

Das Sigmoid ist daher unverzichtbar für Aufgaben wie die Vorhersage von binären Ergebnissen (Ja/Nein- oder Richtig/Falsch-Entscheidungen) und für fundierte Vorhersagen in Klassifizierungsmodellen für maschinelles Lernen . Im weiteren Verlauf dieses Tutoriums werde ich die mathematischen Eigenschaften, Anwendungen und auch einige ihrer Grenzen erklären.

Was ist die Sigmoidfunktion?

Im Kern ist die Sigmoidfunktion eine mathematische Gleichung, die jede reelle Zahl auf einen Wert zwischen 0 und 1 abbildet , was sie ideal für probabilistische Ausgaben macht . Die Formel lautet wie folgt: 

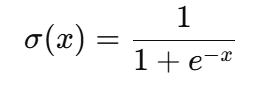
Wo:

• x ist die Eingabe für die Funktion.
• e ist die Basis des natürlichen Logarithmus (ungefähr 2,718). 

Die Sigmoidfunktion wird in der Datenwissenschaft vor allem auf zwei Arten verwendet:

• Binäre Klassifizierung: Die Sigmoid-Funktion wandelt die Ausgabe eines Modells in eine Wahrscheinlichkeitsbewertung um, die dann für Aufgaben wie die Vorhersage von Kreditausfällen, die Erkennung von Betrug oder die Identifizierung von Spam-E-Mails verwendet werden kann.
• Aktivierungsfunktion: In neuronalen Netzen fügt die Sigmoidfunktion Nichtlinearität hinzu, wodurch das Modell komplexe Muster in den Daten lernen kann.

Mathematische Eigenschaften der Sigmoidfunktion

Die Sigmoidfunktion weist mehrere mathematische Eigenschaften auf, die sie zu einer beliebten Wahl für verschiedene Anwendungen machen. 

Wichtige Eigenschaften

• Reichweite: Die Ausgabewerte der Sigmoidfunktion liegen immer zwischen 0 und 1, weshalb sie sich gut für die Schätzung von Wahrscheinlichkeiten bei Aufgaben wie der binären Klassifizierung eignet.
• Monotonie: Die Funktion ist monoton steigend, d.h. wenn der Eingabewert steigt, steigt auch der Ausgabewert, nimmt aber nie ab. Diese Konsistenz ist hilfreich bei der Modellierung von Beziehungen zwischen Variablen.
• Differenzierbarkeit: Die Sigmoidfunktion ist vollständig differenzierbar, d.h. du kannst ihre Ableitung an jedem Punkt berechnen. Diese Eigenschaft ist entscheidend für Optimierungsverfahren wie die Backpropagation, die zum Trainieren neuronaler Netze verwendet wird. 
• Nicht-Linearität: Die Sigmoidfunktion führt Nichtlinearität ein, wodurch die Modelle komplexere Muster und Entscheidungsgrenzen lernen können. Das ist wichtig für Aufgaben, bei denen einfache lineare Beziehungen nicht ausreichen.

Visualisierung der Sigmoid-Funktion

Die charakteristische S-förmige Kurve der Sigmoidfunktion ist ihr auffälligstes Merkmal. Diese Kurve zeigt, wie Eingangswerte in den Bereich von 0 bis 1 gequetscht werden.

Hier ist eine einfache Visualisierung:

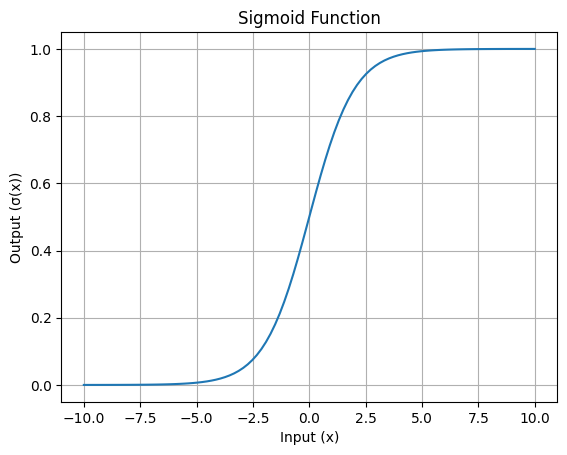
S-förmige Kurve der Sigmoid-Funktion: Bild vom Autor

Die Rolle des Sigmoid in der logistischen Regression

In logistischen Regressionwird die Sigmoid-Funktion verwendet, um die lineare Kombination von Eingangsmerkmalen in einen Wahrscheinlichkeitswert umzuwandeln:

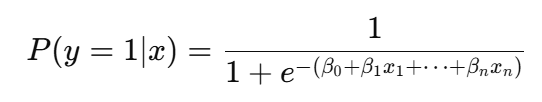
Genauer gesagt wird die Sigmoidfunktion zur Modellierung von binären Ergebnissen verwendet, d. h. sie hilft bei der Vorhersage, ob etwas zu einer von zwei Kategorien gehört, z. B. "ja" oder "nein", "Standard" oder "kein Standard", "Spam" oder "kein Spam".

Die Funktion nimmt das Ergebnis einer linearen Kombination von Eingangsmerkmalen und wandelt es in einen Wahrscheinlichkeitswert zwischen 0 und 1 um. Diese Wahrscheinlichkeit gibt an, wie wahrscheinlich es ist, dass die Eingabe zu einer bestimmten Klasse gehört.

Wenn die Ausgabe der linearen Gleichung zum Beispiel zwei ist, wandelt die Sigmoid-Funktion dies in eine Wahrscheinlichkeit um (z. B. 0,88), die eine Wahrscheinlichkeit von 88 % angibt, dass die Eingabe zur positiven Klasse gehört. Angenommen, der Schwellenwert wird auf 0,5 gesetzt, der die Klassifizierung bestimmt. Wenn der Wahrscheinlichkeitswert nun über 0,5 liegt, sagt das Modell die positive Klasse voraus; andernfalls sagt es die negative Klasse voraus.

Warum ist diese Umwandlung überhaupt notwendig? Das ist notwendig, weil die Rohdaten des linearen Modells nicht direkt als Wahrscheinlichkeiten interpretiert werden können. Durch die Verwendung der Sigmoid-Funktion liefert die logistische Regression nicht nur Klassifizierungen, sondern auch ein klares probabilistisches Verständnis, das besonders bei Anwendungen wie der Risikovorhersage, der Abwanderungsklassifizierung oder der Betrugserkennung nützlich ist. Diese probabilistische Interpretation ermöglicht es den Entscheidungsträgern, individuelle Schwellenwerte auf der Grundlage der spezifischen Anforderungen einer Aufgabe festzulegen.

Anwendungen in neuronalen Netzen

Die Sigmoidfunktion spielt in neuronalen Netzen als Aktivierungsfunktion eine zentrale Rolle.

Rolle der Aktivierungsfunktion

Die Hauptaufgabe der Sigmoidfunktion als Aktivierungsfunktion besteht darin, die gewichtete Summe der Eingaben aus der vorherigen Schicht in einen Ausgabewert zwischen 0 und 1 zu verwandeln. Diese Umwandlung ist nützlich, um Nichtlinearität in das Modell einzubringen. Dadurch können die verborgenen Schichten in einem tiefen neuronalen Netz komplexe Zusammenhänge lernen und Probleme lösen, die nicht mit geraden Linien getrennt werden können, wie z. B. Bilderkennung oder natürliche Sprachverarbeitung.

Das Problem des verschwindenden Gradienten

Die Sigmoidfunktion hat jedoch ihre Grenzen, wobei die wichtigste das Problem des verschwindenden Gradienten ist. Bei sehr großen oder sehr kleinen Eingangswerten geht die Ausgabe der Funktion in die Sättigung nahe 1 oder 0, und ihre Steigung wird fast null. Das führt dazu, dass sich der Lernprozess in dichten neuronalen Netzen verlangsamt, weil die Gewichte beim Training zu langsam aktualisiert werden.

Alternative Aktivierungsfunktionen

Um dieser Einschränkung zu begegnen, werden oft andere Aktivierungsfunktionen wie ReLU (Rectified Linear Unit) und Tanh verwendet. ReLU ist rechnerisch einfacher und vermeidet das Problem des verschwindenden Gradienten für positive Eingaben. Tanh ist wie Sigmoid S-förmig, gibt aber Werte zwischen -1 und 1 aus, was es null-zentriert und in bestimmten Szenarien effizienter macht. Diese Alternativen haben das Sigmoid in tiefen Netzen weitgehend ersetzt, außer in den Ausgabeschichten für Aufgaben wie die binäre Klassifizierung.

Wichtige Erwägungen und Beschränkungen

Die Sigmoidfunktion hat zwar viele Vorteile, aber sie bringt auch einige Herausforderungen mit sich, die ihre Leistung in bestimmten Situationen beeinträchtigen können. 

Sättigungsproblem

Die Sigmoidfunktion kann sättigen, wenn die Eingangswerte zu groß (positiv) oder zu klein (negativ) sind. Sättigung bedeutet, dass der Output sehr nahe an 0 oder 1 herankommt und die Steigung (Veränderungsrate) fast Null wird. 

Das ist problematisch, denn wenn der Gradient nahe Null ist, hat das Modell Schwierigkeiten, beim Training zu lernen. Folglich verlangsamt dies die Aktualisierungen in gradientenbasierten Optimierungsmethoden wie Backpropagation.

Null-zentrierte Ausgabe

Eine weitere Einschränkung der Sigmoidfunktion ist, dass ihr Ausgang zwischen 0 und 1 liegt und sie nicht null-zentriert ist. Das bedeutet, dass alle Ausgaben positiv sind, was die Verteilung der Eingaben in einem neuronalen Netz verschieben und die Optimierung langsamer machen kann. Im Gegensatz dazu haben Funktionen wie Tanh Ausgänge im Bereich von -1 bis 1, was dazu beiträgt, den Mittelwert der Aktivierungen näher bei Null zu halten, was die Konvergenz beschleunigt.

Berechnungsaufwand

Die Sigmoidfunktion basiert auf der Exponentialfunktion, die im Vergleich zu einfacheren Aktivierungsfunktionen wie ReLU (Rectified Linear Unit) sehr rechenintensiv ist. Die sigmoidale Formel lautet zum Beispiel:

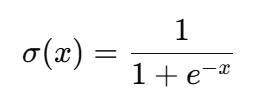
Hier ist die Exponentialrechnung rechenintensiver als die Operationen in ReLU, die nur Vergleiche und lineare Funktionen beinhalten, und wird wie folgt angegeben:

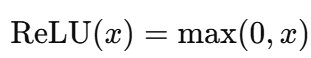
Bei modernen neuronalen Netzen, vor allem bei solchen mit vielen Schichten und Neuronen, summieren sich die Kosten für die wiederholte Durchführung der Exponentialoperation, und hier kommen die Alternativen zum Einsatz.

Fazit

Die Sigmoidfunktion ist ein wichtiges Werkzeug in der Datenwissenschaft, insbesondere für Aufgaben wie die logistische Regression und als Aktivierungsfunktion in neuronalen Netzen. Sie hilft dabei, Eingaben in Wahrscheinlichkeiten umzuwandeln und führt Nichtlinearität in die Modelle ein, so dass sie in der Lage sind, komplexe Muster zu verarbeiten. Allerdings gibt es auch Herausforderungen wie Sättigung, fehlende null-zentrierte Ausgänge und höhere Rechenkosten, die seine Effizienz in tiefen Netzen beeinträchtigen können.

Obwohl moderne Techniken Alternativen eingeführt haben, kann die Bedeutung der Sigmoidfunktion für die Entwicklung von Data Science-Methoden nicht hoch genug eingeschätzt werden. Wenn du tiefer in die Funktionsweise eintauchen und sie in Aktion sehen willst, solltest du unsere interaktiven Kurse und Tutorials zu neuronalen Netzen und logistischer Regression ausprobieren. Unsere Einführung in Deep Learning in Python ist eine gute Option.