Los datos de series temporales son datos recogidos sobre el mismo tema en distintos momentos, como el PIB de un país por año, el precio de las acciones de una empresa concreta durante un periodo de tiempo, o tus propios latidos del corazón registrados a cada segundo. Cualquier dato que puedas capturar de forma continua en diferentes intervalos de tiempo es una forma de datos de series temporales.
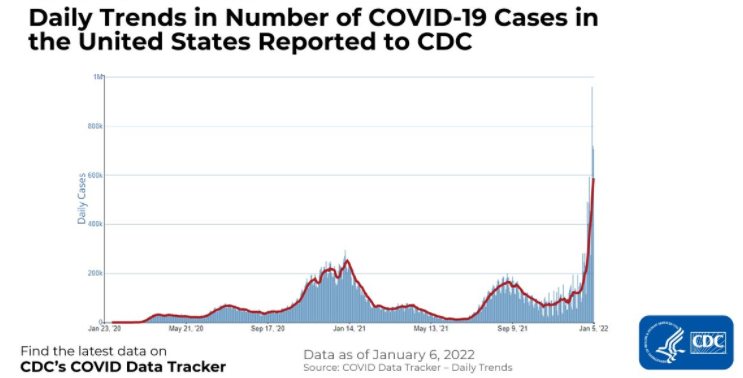
A continuación se muestra un ejemplo de datos de series temporales que muestran el número de casos de COVID-19 en Estados Unidos notificados a los CDC. El eje x muestra el paso del tiempo y el eje y representa el número de casos de COVID-19 en miles.
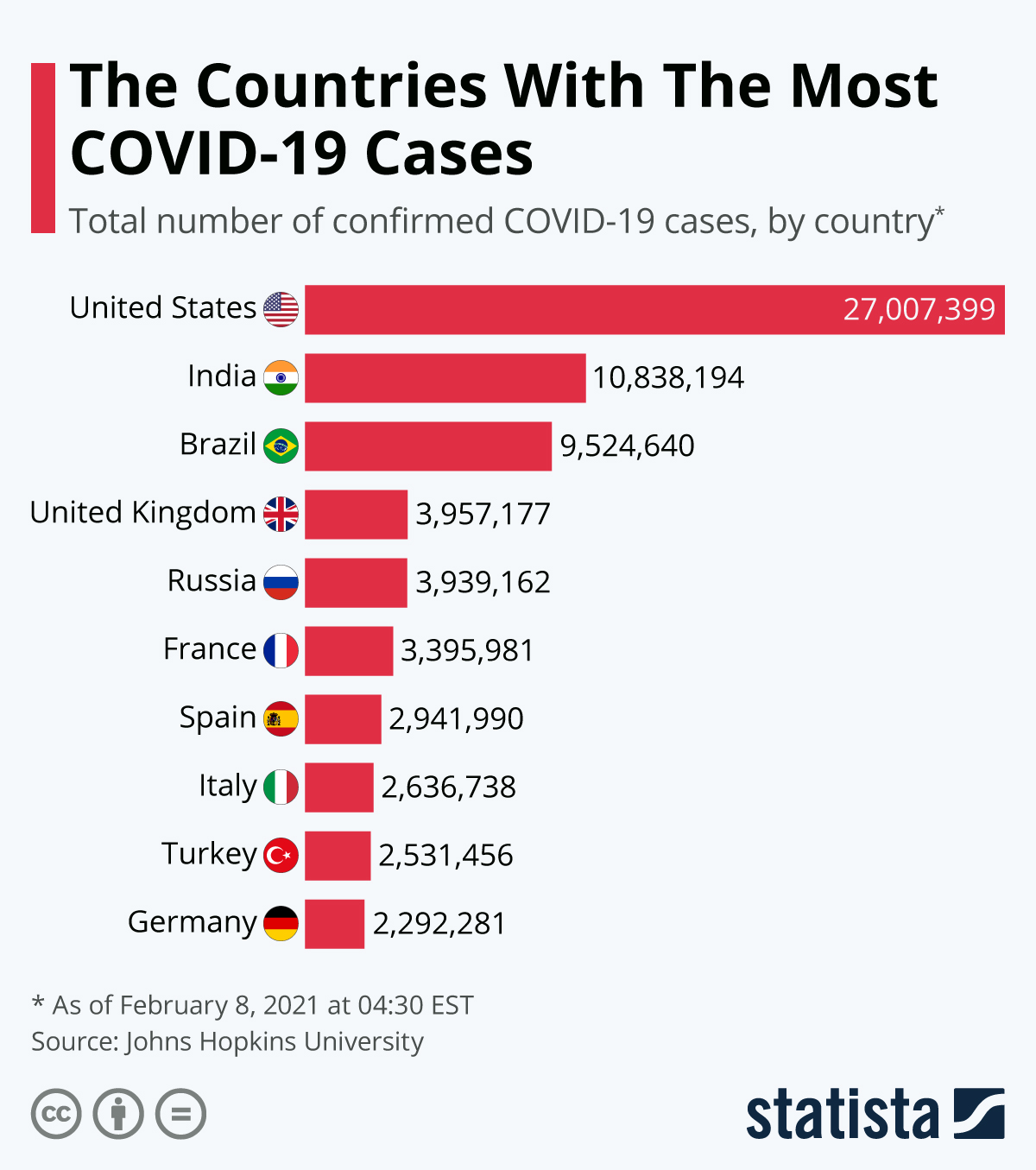
Por otro lado, los conjuntos de datos más convencionales que almacenan información en un único punto en el tiempo, como información sobre clientes, productos y empresas, etc., se conocen como datos transversales. Un ejemplo de esto se muestra en el conjunto de datos siguiente, que rastrea los países con más casos de COVID-19 en un periodo de tiempo fijo y coherente para todos los países.
No es muy difícil distinguir la diferencia entre los datos transversales y los de series temporales, ya que los objetivos de análisis de ambos conjuntos de datos son muy distintos. En nuestros ejemplos, primero nos interesaba hacer un seguimiento de los casos de COVID-19 a lo largo de un periodo de tiempo, antes de analizar los casos de COVID-19 por país en un periodo de tiempo fijo.
Es probable que un conjunto de datos típico del mundo real sea un híbrido de estos formatos. Por ejemplo, podemos pensar en un minorista como Walmart que vende miles de productos cada día. Si analizas las ventas por producto en un día concreto, se tratará de un análisis transversal. Por ejemplo, podrías querer averiguar cuál es el artículo número 1 en ventas en Nochebuena. Comparativamente, si quisieras averiguar la venta de un artículo concreto durante un periodo de tiempo (digamos los últimos 5 años), se trataría de un análisis de series temporales.
Los objetivos son distintos cuando se analizan series temporales y datos transversales, y es probable que un conjunto de datos del mundo real sea un híbrido tanto de series temporales como de datos transversales.
¿Qué es la previsión de series temporales?
La previsión de series temporales es exactamente lo que parece: predecir valores desconocidos. La previsión de series temporales consiste en recopilar datos históricos, prepararlos para que los consuman los algoritmos y, a continuación, predecir los valores futuros basándose en patrones aprendidos de los datos históricos.
Hay numerosas razones por las que las empresas pueden estar interesadas en prever valores futuros, concretamente el PIB, las ventas mensuales, las existencias, el desempleo y las temperaturas globales:
- Un minorista puede estar interesado en predecir las ventas futuras a nivel de SKU (unidad de mantenimiento de existencias) para planificar y presupuestar.
- A un pequeño comerciante puede interesarle prever las ventas por tienda, para poder programar los recursos adecuados (más personal en los periodos de mayor afluencia y viceversa).
- A un gigante del software como Google puede interesarle conocer la hora del día o el día de la semana de mayor actividad, para poder programar los recursos del servidor en consecuencia.
- El departamento de sanidad puede estar interesado en predecir el cúmulo de vacunas COVID administradas para poder predecir mejor cuándo se espera que se ponga en marcha la inmunidad de rebaño.
Tipo de previsión de series temporales
Hay tres tipos de previsión de series temporales. El que debas utilizar dependerá del tipo de datos que manejes y del caso de uso que tengas entre manos:
Previsión univariante
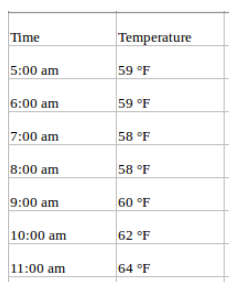
Una serie temporal univariante, como su nombre indica, es una serie con una única variable dependiente del tiempo. Por ejemplo, si haces un seguimiento de los valores horarios de temperatura de una región determinada y quieres prever la temperatura futura utilizando las temperaturas históricas, se trata de una previsión de series temporales univariantes. Tus datos pueden tener este aspecto:
Previsión multivariante
En cambio, una serie temporal Multivariante tiene más de una variable dependiente del tiempo. Cada variable depende no sólo de sus valores pasados, sino que también tiene cierta dependencia de otras variables. Esta dependencia se utiliza para prever valores futuros.
Consideremos el ejemplo anterior y supongamos que nuestro conjunto de datos incluye otros atributos relacionados con el tiempo durante el mismo periodo de tiempo, como el porcentaje de transpiración, el punto de rocío, la velocidad del viento, etc., junto con los valores de temperatura. En este caso, hay que tener en cuenta múltiples variables para predecir de forma óptima la temperatura. Una serie como ésta entraría en la categoría de series temporales multivariantes. Tu conjunto de datos tendrá ahora este aspecto:
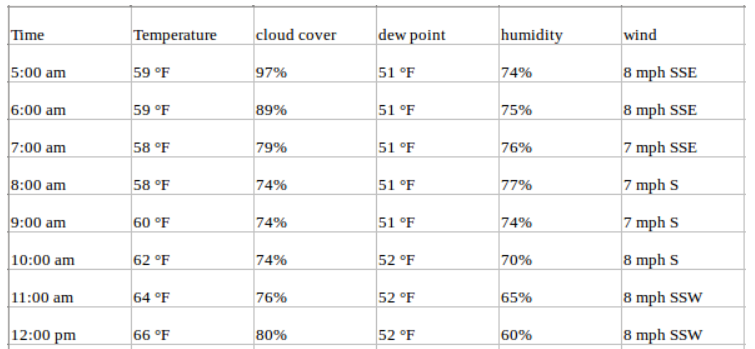
Sigues previendo valores de temperatura para el futuro, pero ahora puedes utilizar otra información disponible en tu previsión, ya que suponemos que los valores de temperatura también dependerán de estos factores.
 Fuente de la imagen: Van Nguyen
Fuente de la imagen: Van Nguyen
Cuando nos ocupamos de la previsión multivariante de series temporales, las variables de entrada pueden ser de dos tipos:
- Exógeno: Variables de entrada que no están influidas por otras variables de entrada y de las que depende la variable de salida.
- Endógeno: Variables de entrada en las que influyen otras variables de entrada y de las que depende la variable de salida.
Este tutorial tratará sobre varios modelos clásicos, pero no todos admiten la previsión de series temporales multivariantes. En situaciones como ésta, los modelos de aprendizaje automático vienen al rescate, ya que puedes modelar cualquier problema de previsión de series temporales con regresión. Veremos un ejemplo de esto más adelante en este tutorial.
Métodos de previsión de series temporales
La previsión de series temporales puede clasificarse, a grandes rasgos, en las siguientes categorías:
- Modelos Clásicos / Estadísticos - Medias Móviles, Suavizado Exponencial, ARIMA, SARIMA, TBATS
- Aprendizaje automático - Regresión lineal, XGBoost, Random Forest o cualquier modelo ML con métodos de reducción
- Aprendizaje profundo - RNN, LSTM
Este tutorial se centra en los dos primeros métodos: los modelos clásicos/estadísticos y el aprendizaje automático. Los métodos de aprendizaje profundo están fuera del alcance de este tutorial.
Modelos estadísticos
Cuando se trata de prever series temporales utilizando modelos estadísticos, hay bastantes algoritmos populares y bien aceptados. Cada una de ellas tiene modalidades matemáticas distintas y vienen acompañadas de un conjunto diferente de supuestos que deben cumplirse. Este tutorial no profundizará en los conceptos matemáticos, sino que se limitará a dar una intuición que esperamos te resulte útil.
ARIMA
ARIMA es uno de los métodos clásicos más populares para la previsión de series temporales. Son las siglas de media móvil integrada autorregresiva y es un tipo de modelo que pronostica series temporales dadas basándose en sus propios valores pasados, es decir, sus propios retardos y los errores de pronóstico retardados. El ARIMA consta de tres componentes:
- Autoregresión (AR): se refiere a un modelo que muestra una variable cambiante que hace regresión sobre sus propios valores retardados, o anteriores.
- Integrado (I): representa la diferenciación de las observaciones brutas para permitir que la serie temporal se vuelva estacionaria (es decir, los valores de los datos se sustituyen por la diferencia entre los valores de los datos y los valores anteriores).
- Media móvil (MA): incorpora la dependencia entre una observación y un error residual de un modelo de media móvil aplicado a observaciones retardadas.
La parte "AR" de ARIMA indica que la variable evolutiva de interés hace una regresión sobre sus propios valores retardados (es decir, observados con anterioridad). La parte "MA" indica que el error de regresión es en realidad una combinación lineal de términos de error cuyos valores se produjeron contemporáneamente y en distintos momentos del pasado. La "I" (de "integrado") indica que los valores de los datos se han sustituido por la diferencia entre sus valores y los valores anteriores (y este proceso de diferenciación puede haberse realizado más de una vez). La finalidad de cada una de estas características es hacer que el modelo se ajuste lo mejor posible a los datos.
SARIMA
Una extensión de ARIMA que permite modelizar directamente el componente estacional de la serie se denomina SARIMA. Un problema del modelo ARIMA es que no admite datos estacionales. Se trata de una serie temporal con un ciclo que se repite. ARIMA espera datos que no sean estacionales o a los que se haya eliminado el componente estacional, por ejemplo, ajustados estacionalmente mediante métodos como la diferenciación estacional. SARIMA añade tres nuevos hiperparámetros para especificar la autoregresión (AR), la diferenciación (I) y la media móvil (MA) para el componente estacional de la serie.
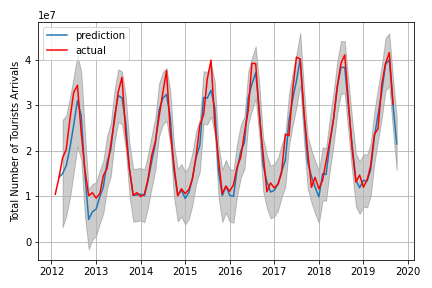 Previsión mediante el modelo Previsión mediante el modelo SARIMA
Previsión mediante el modelo Previsión mediante el modelo SARIMA
Suavizado exponencial
El alisamiento exponencial es un método de previsión de series temporales para datos univariantes. Puede ampliarse para admitir datos con un componente tendencial o estacional. Puede utilizarse como alternativa a la popular familia de modelos ARIMA.
El suavizado exponencial de los datos de series temporales asigna ponderaciones exponencialmente decrecientes para las observaciones más nuevas a las más antiguas. Cuanto más antiguos son los datos, menos peso se les da, mientras que a los datos más recientes se les da más peso
- El alisamiento exponencial simple (sencillo) utiliza una media móvil ponderada con ponderaciones exponencialmente decrecientes.
- El suavizado exponencial de Holt suele ser más fiable para manejar datos que muestran tendencias.
- El suavizado exponencial triple (también llamado Holt-Winters Multiplicativo) es más fiable para las tendencias parabólicas o los datos que muestran tendencias y estacionalidad.
TBATS
Los modelos TBATS son para datos de series temporales con estacionalidad múltiple. Por ejemplo, los datos de ventas al por menor pueden tener un patrón diario y un patrón semanal, así como un patrón anual.
En el TBATS, se aplica una transformación Box-Cox a la serie temporal original, y luego ésta se modela como una combinación lineal de una tendencia suavizada exponencialmente, un componente estacional y un componente ARMA.
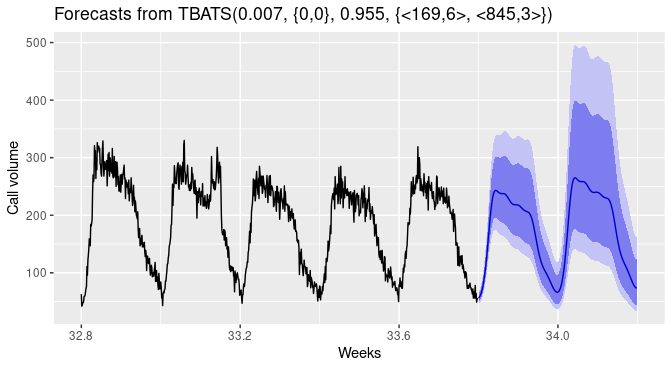 con Previsión con TBATS
con Previsión con TBATS
Aprendizaje automático
Si no quieres utilizar modelos estadísticos o no funcionan bien, puedes probar este método. El aprendizaje automático es una forma alternativa de modelizar datos de series temporales para hacer previsiones. En este método, extraemos características de la fecha para añadirlas a nuestra "variable X" y el valor de la serie temporal es la "variable y". Veamos un ejemplo:
Para este tutorial, he utilizado el conjunto de datos de pasajeros de líneas aéreas de EE.UU. que se puede descargar de Kaggle.
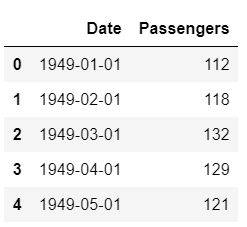 Conjunto de datos Muestra
Conjunto de datos Muestra
Podemos extraer características de la columna "Fecha", como el mes, el año, la semana del año, etc. Ver ejemplo:
# extract month and year from dates
data['Month'] = [i.month for i in data['Date']]
data['Year'] = [i.year for i in data['Date']]
# create a sequence of numbers
data['Series'] = np.arange(1,len(data)+1)
# drop unnecessary columns and re-arrange
data.drop(['Date', 'MA12'], axis=1, inplace=True)
data = data[['Series', 'Year', 'Month', 'Passengers']]
# check the head of the dataset
data.head()
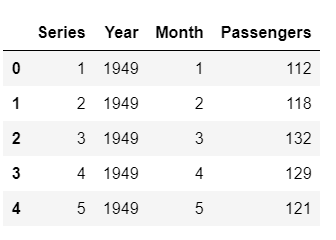 Filas de tras extraer las características Filas de muestra tras extraer las características
Filas de tras extraer las características Filas de muestra tras extraer las características
Hay que tener en cuenta que la división entrenamiento-prueba para datos de series temporales es especial. Como no puedes cambiar el orden de la tabla, tienes que asegurarte de que no muestreas aleatoriamente, ya que quieres que tus datos de prueba contengan puntos que estén en el futuro de los puntos de los datos del tren (el tiempo siempre avanza).
# split data into train-test set
train = data[data['Year'] < 1960]
test = data[data['Year'] >= 1960]
# check shape
train.shape, test.shape
>>> ((132, 4), (12, 4))
Ahora que hemos hecho la división entrenamiento-prueba, estamos listos para entrenar un modelo de aprendizaje automático en los datos de entrenamiento, puntuarlo en los datos de prueba y evaluar el rendimiento de nuestro modelo. En este ejemplo, utilizaré PyCaret, una biblioteca de aprendizaje automático de código abierto y bajo código en Python que automatiza los flujos de trabajo de aprendizaje automático. Para utilizar PyCaret, tienes que instalarlo mediante pip.
# install pycaret
pip install pycaret
Si necesitas ayuda durante la instalación, consulta la documentación oficial.
Suponiendo que hayas instalado PyCaret correctamente:
# import the regression module
from pycaret.regression import *
# initialize setup
s = setup(data = train, test_data = test, target = 'Passengers', fold_strategy = 'timeseries', numeric_features = ['Year', 'Series'], fold = 3, transform_target = True, session_id = 123)
Ahora, para entrenar modelos de aprendizaje automático, sólo tienes que ejecutar una línea:
best = compare_models(sort = 'MAE')
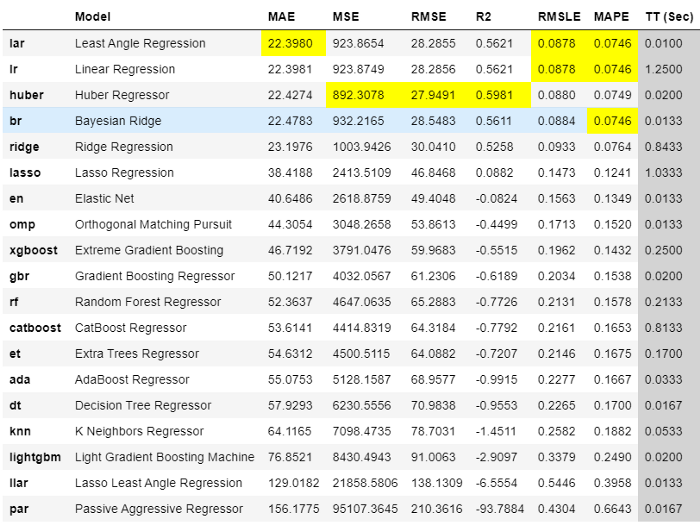 de Salida de comparar_modelos
de Salida de comparar_modelos
El mejor modelo utilizando la validación cruzada de 3 pliegues basada en el Error Medio Absoluto (MAE) es la Regresión de Ángulo Arrendado. Ahora podemos utilizar este modelo para prever el futuro. Para ello, tenemos que crear "variables X" en el futuro. Esto puede hacerse creando fechas futuras y extrayendo luego características de ellas.
Como hemos entrenado nuestro modelo con los datos hasta 1960, vamos a predecir cinco años en el futuro, hasta 1965. Para utilizar nuestro modelo final para generar predicciones futuras, primero tenemos que crear un conjunto de datos formado por la columna Mes, Año, Serie en las fechas futuras. Este código crea el futuro conjunto de datos "X".
future_dates = pd.date_range(start = '1961-01-01', end = '1965-01-01', freq = 'MS')
future_df = pd.DataFrame()
future_df['Month'] = [i.month for i in future_dates]
future_df['Year'] = [i.year for i in future_dates]
future_df['Series'] = np.arange(145,(145+len(future_dates)))
future_df.head()
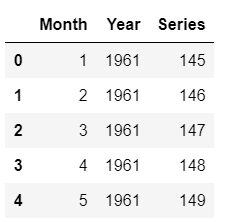 Filas de de futuro_df Filas de muestra de futuro_df
Filas de de futuro_df Filas de muestra de futuro_df
Ahora podemos utilizar futuro_df para hacer predicciones:
predictions_future = predict_model(best, data=future_df)
predictions_future.head()
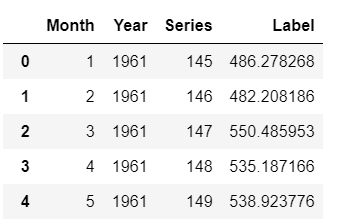 Salida de .head() Salida de predictions_future.head()
Salida de .head() Salida de predictions_future.head()
Y ahora podemos trazarlo:
concat_df = pd.concat([data,predictions_future], axis=0)
concat_df_i = pd.date_range(start='1949-01-01', end = '1965-01-01', freq = 'MS')
concat_df.set_index(concat_df_i, inplace=True)
fig = px.line(concat_df, x=concat_df.index, y=["Passengers", "Label"], template = 'plotly_dark')
fig.show()
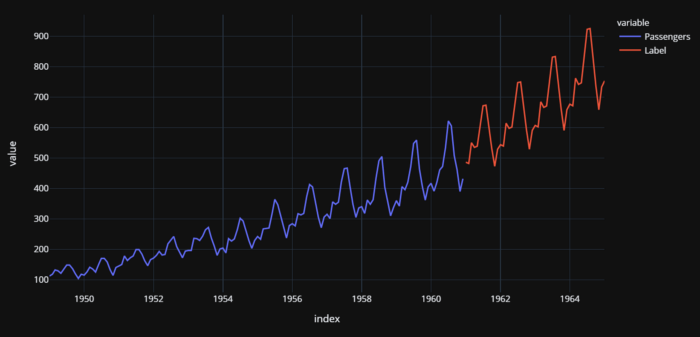 de líneas aéreas reales (1949-1960) y previstos (1961-1964) Pasajeros de líneas aéreas estadounidenses reales (1949-1960) y previstos (1961-1964
de líneas aéreas reales (1949-1960) y previstos (1961-1964) Pasajeros de líneas aéreas estadounidenses reales (1949-1960) y previstos (1961-1964
Hay que tener en cuenta algunos elementos importantes. Siempre que trates con series temporales univariantes puedes convertirlas en problemas de regresión y resolverlos como en este ejemplo. Sin embargo, debes tener cuidado con la validación cruzada. No puedes hacer validación cruzada aleatoria en modelos de series temporales y debes utilizar técnicas apropiadas para series temporales.En este ejemplo, PyCaret utiliza TimeSeriesSplit de la biblioteca scikit-learn.
Frameworks Python para Previsión
Facebook Profeta
Prophet es un software de código abierto publicado por el equipo de Ciencia de Datos Fundamentales de Facebook. Se puede descargar en CRAN y PyPI.
Prophet es un procedimiento de previsión de datos de series temporales basado en un modelo aditivo en el que se ajustan tendencias no lineales con estacionalidad anual, semanal y diaria, además de efectos de vacaciones. Funciona mejor con series temporales que tengan fuertes efectos estacionales y varias temporadas de datos históricos. Prophet es resistente a los datos que faltan y a los cambios de tendencia, y suele manejar bien los valores atípicos.
Para saber más, consulta este enlace.
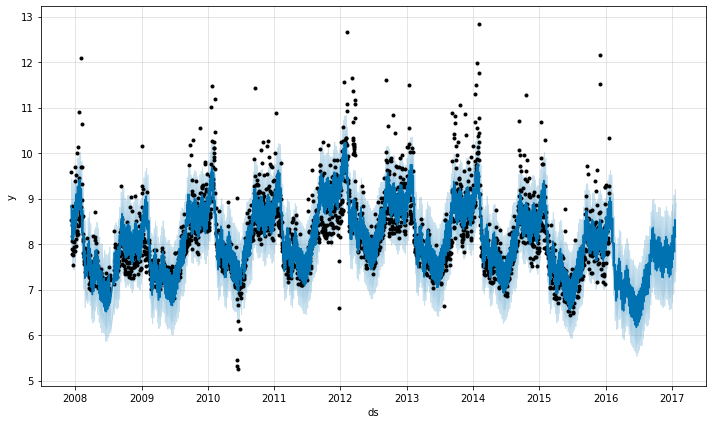 con FB Prophet Previsión con FB Prophet
con FB Prophet Previsión con FB Prophet
sktime
sktime es un marco unificado de código abierto para el aprendizaje automático con series temporales. Proporciona una plataforma fácil de usar, flexible y modular para una amplia gama de tareas de aprendizaje automático de series temporales. Ofrece interfaces compatibles con scikit-learn y herramientas de composición de modelos, con el objetivo de que el ecosistema sea más utilizable e interoperable en su conjunto.
 Para saber más sobre sktime, consulta este enlace.
Para saber más sobre sktime, consulta este enlace.
pmdarima
Pmdarima es una biblioteca estadística diseñada para llenar el vacío en las capacidades de análisis de series temporales de Python. Esto incluye
- El equivalente de la funcionalidad auto.arima de R
- Una colección de pruebas estadísticas de estacionariedad y estacionalidad
- Descomposiciones estacionales de series temporales
- Utilidades de validación cruzada
- Una rica colección de conjuntos de datos de series temporales incorporados para la creación de prototipos y ejemplos
Para saber más sobre pmdarima, consulta esta página.
Kats
Kats es otro increíble proyecto de código abierto de Facebook, lanzado por su equipo de Ciencia de Datos de Infraestructura. Se puede descargar en PyPI.
Kats es un conjunto de herramientas para analizar datos de series temporales; un marco ligero, fácil de usar y generalizable para realizar análisis de series temporales. El objetivo de Kats es proporcionar una ventanilla única para el análisis de series temporales, incluyendo detección, previsión, extracción/incrustación de características y análisis multivariante, etc.
 con KATS Previsión con KATS
con KATS Previsión con KATS
Para saber más sobre los KATS, consulta este enlace.
Órbita
Orbit es un increíble proyecto de código abierto de Uber. Es una biblioteca de Python para la previsión bayesiana de series temporales. Proporciona una interfaz familiar e intuitiva de inicialización-ajuste-predicción para tareas de series temporales, a la vez que utiliza lenguajes de programación probabilísticos bajo el capó.
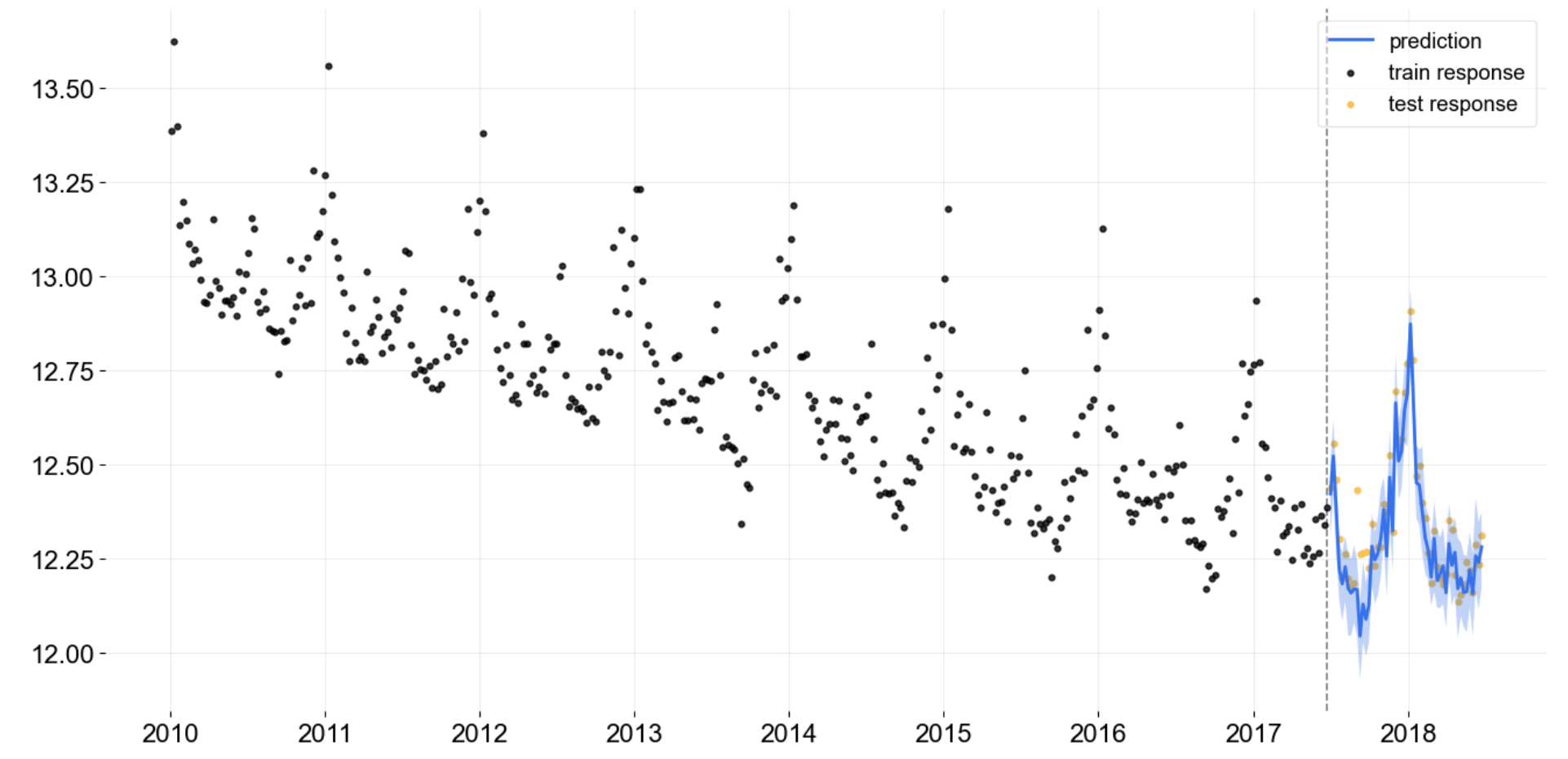 mediante órbita Previsión mediante órbita
mediante órbita Previsión mediante órbita
Para saber más sobre Orbit, consulta este enlace.
PyCaret
PyCaret es una biblioteca de aprendizaje automático de código abierto y bajo código en Python que automatiza los flujos de trabajo de aprendizaje automático. Con PyCaret, pasarás menos tiempo codificando y más tiempo analizando. Puedes entrenar tu modelo, analizarlo, iterar más rápido que nunca y desplegarlo instantáneamente como una API REST o incluso crear una sencilla aplicación ML front-end, todo ello desde tu bloc de notas favorito.
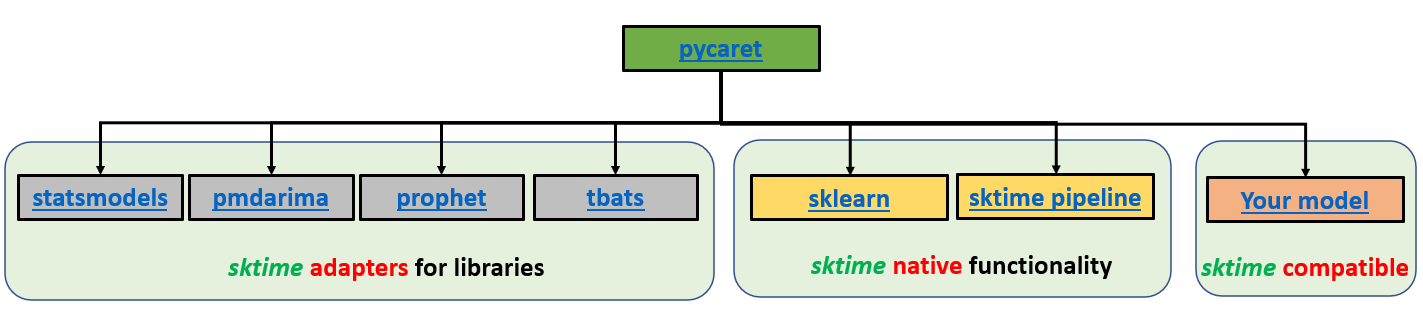 Arquitectura del Módulo de Series Temporales de PyCaret. Desarrollado por el desarrollador jefe Nikhil Gupta.
Arquitectura del Módulo de Series Temporales de PyCaret. Desarrollado por el desarrollador jefe Nikhil Gupta.
A continuación, veremos un ejemplo de una tarea de previsión de series temporales de extremo a extremo utilizando la biblioteca PyCaret.
Ejemplo de extremo a extremo
El módulo de series temporales de PyCaret está disponible en versión beta, puedes descargarlo desde pip.
pip install pycaret-ts-alpha
Enlace a este tutorial en Colab.
Conjunto de datos
Aquí hemos utilizado el conjunto de datos de las aerolíneas, que también está disponible en el repositorio de datos de PyCaret.
from pycaret.datasets import get_data
data = get_data('airlineer')

data.plot()
Configuración Experimento
Los experimentos en PyCaret se inician utilizando la función setup. Esta función se encarga de todos los pasos de preprocesamiento, entrenamiento-prueba-división, estrategia de validación cruzada y algunas tareas más.
from pycaret.time_series import *
s = setup(data, session_id = 123)
 de la función de configuración Salida de la función de configuración
de la función de configuración Salida de la función de configuración
Análisis Exploratorio de Datos (AED)
Cuando se trata de EDA de datos de series temporales univariantes, hay algunas cosas que puedes y debes hacer.
Para utilizar modelos clásicos y estadísticos, puedes realizar algunas pruebas estadísticas. Hay una función en PyCaret que lo hace por ti.
check_stats()
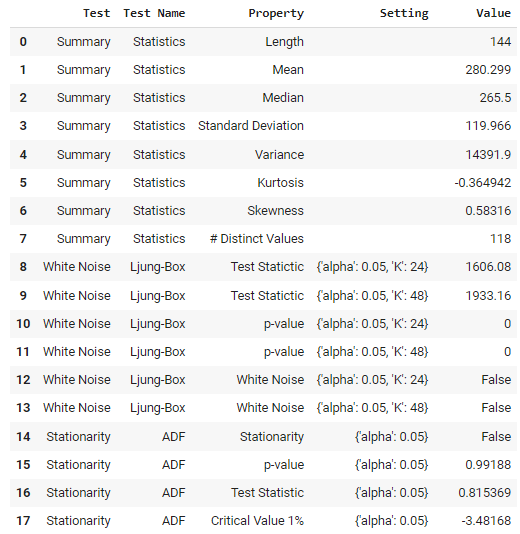 de la función check_stats Salida de la función check_stats
de la función check_stats Salida de la función check_stats
Si tratas con series temporales univariantes, también puedes descomponerlas en componentes de tendencia, estacionalidad y error para cualquier análisis posterior.
plot_model(plot = 'decomp_classical")
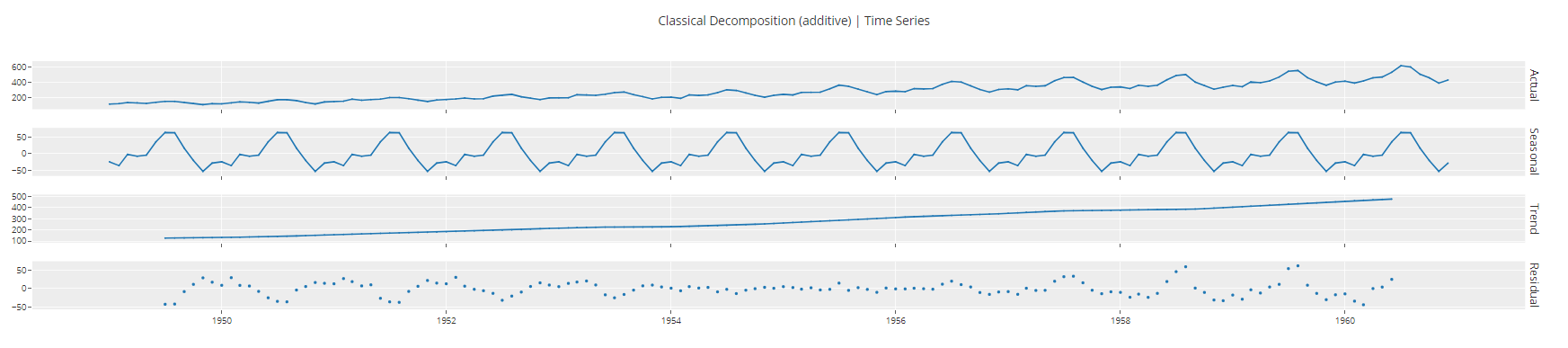 de la zar_modelo Entrenamiento y selección de modelos Salida de la función trazar_modelo<c/entre> ## Entrenamiento y selección de modelos ## Para entrenar varios modelos y seleccionar uno de entre muchos, ejecutamos una sola línea de código.
de la zar_modelo Entrenamiento y selección de modelos Salida de la función trazar_modelo<c/entre> ## Entrenamiento y selección de modelos ## Para entrenar varios modelos y seleccionar uno de entre muchos, ejecutamos una sola línea de código. best = compare_models() 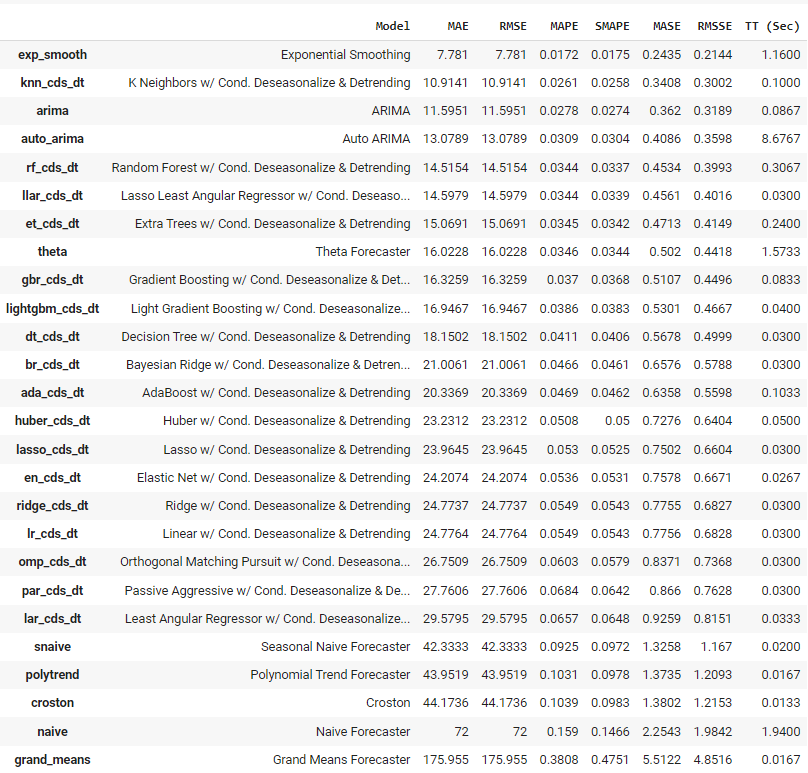 de la función comparar_modelos Salida de la función comparar_modelos
de la función comparar_modelos Salida de la función comparar_modelos
PyCaret ha entrenado más de 25 modelos utilizando la validación cruzada adecuada a las series temporales y ha presentado una lista de modelos ordenados de mayor a menor rendimiento. El mejor modelo basado en este experimento para este conjunto de datos resulta ser el Suavizado exponencial, con un error medio absoluto de 7,781.
Análisis de modelos
Antes de desplegar este modelo para generar predicciones para el futuro, podemos ver un par de gráficos de análisis para comentar la calidad de nuestro modelo.
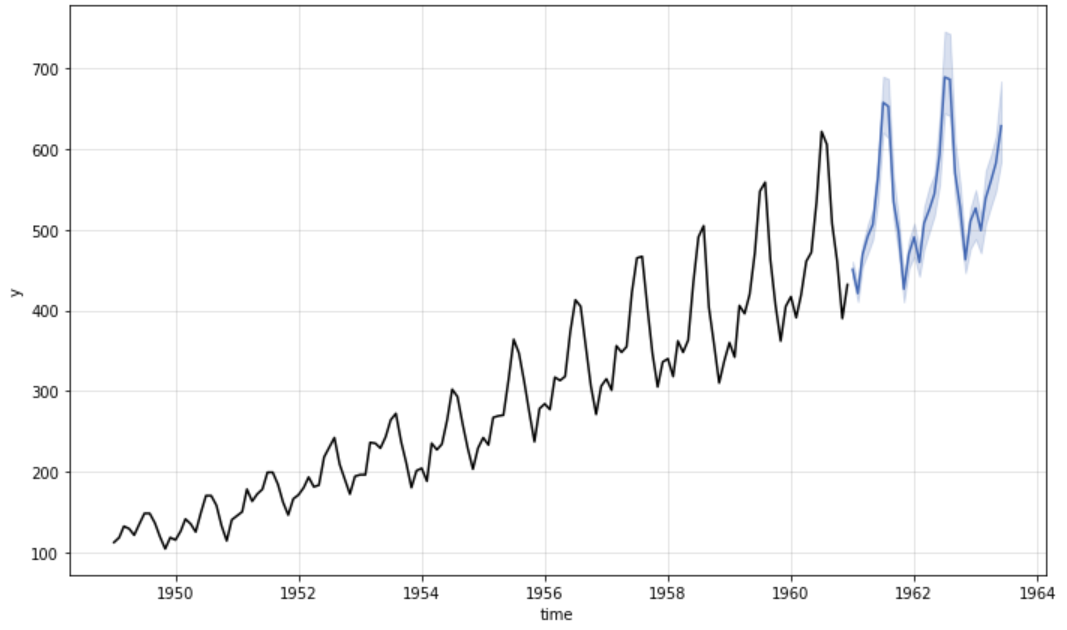
plot_model(best, plot = 'forecast', data_kwargs = {'fh': 24})
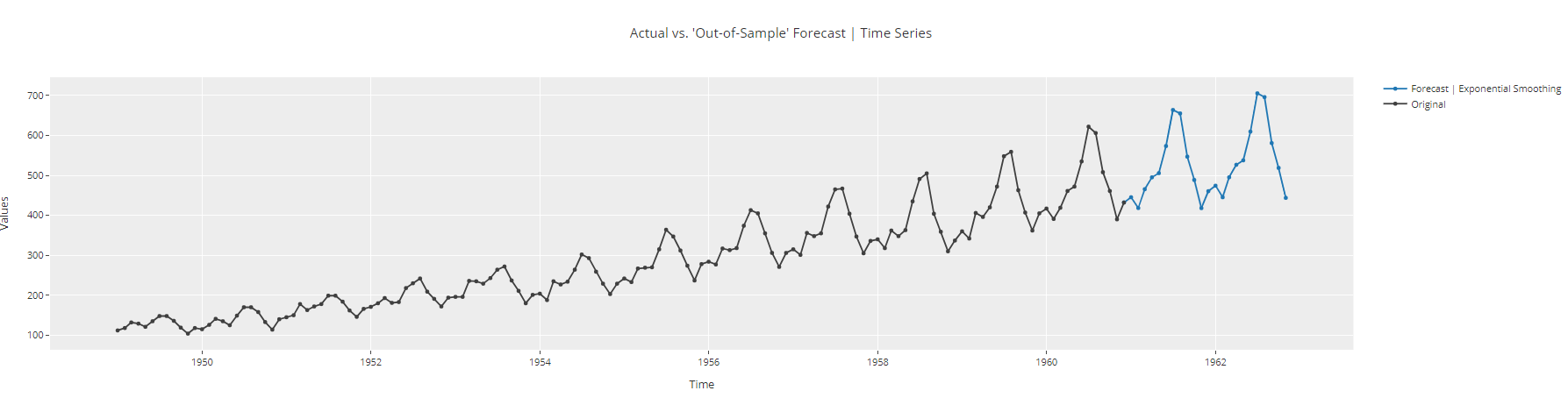 de previsión de series Gráfico de previsión de series temporales
de previsión de series Gráfico de previsión de series temporales
plot_model(best, plot = 'residuals')
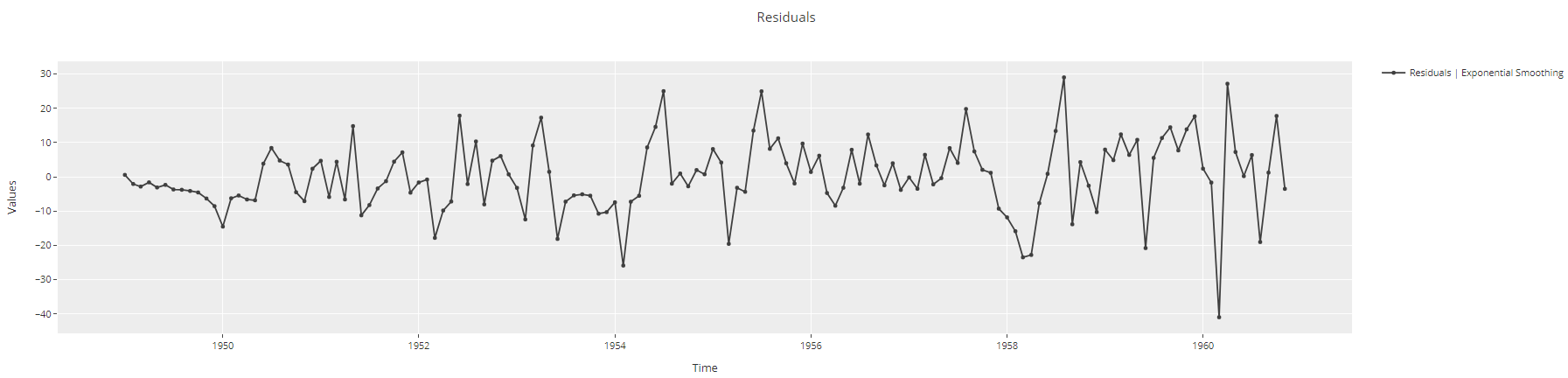 de series de Gráfico de series temporales de residuos
de series de Gráfico de series temporales de residuos
plot_model(best, plot = 'insample')
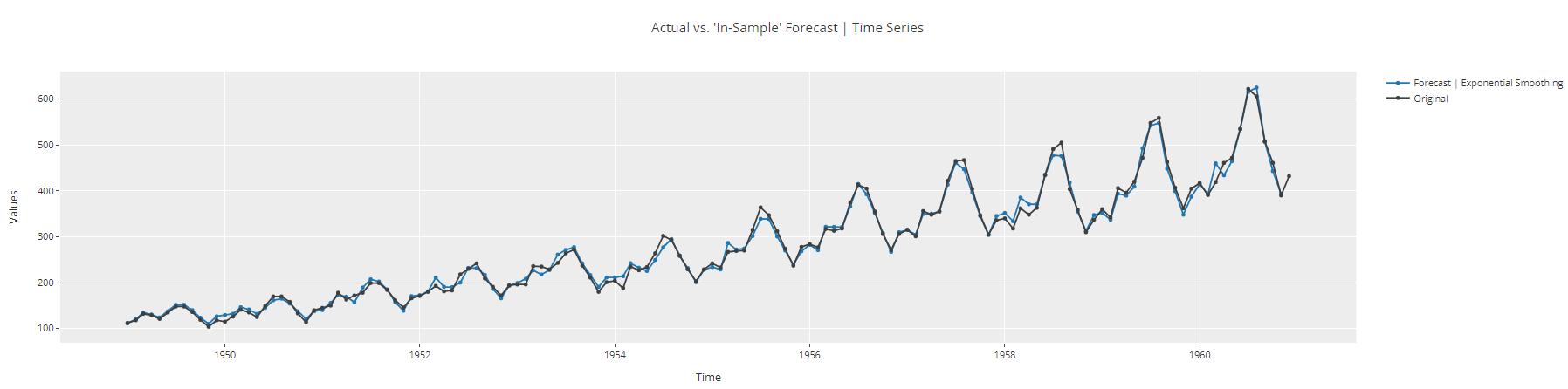 de series temporales sin Gráfico de series temporales sin muestra
de series temporales sin Gráfico de series temporales sin muestra
Despliegue del modelo
Llegados a este punto, estamos listos para finalizar el modelo y guardarlo para utilizarlo en el futuro.
# finalize model
final_best = finalize_model(best)
# save model
final_best = finalize_model(best)

Para volver a cargar este archivo y generar predicciones sobre datos futuros:
# load model
loaded_model = load_model('my_best_model')
# generate predictions for the next 48 months
predict_model(loaded_model, fh = 48)
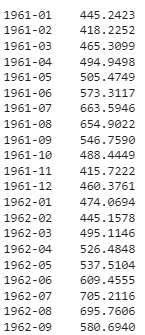 Salida Salida truncada
Salida Salida truncada
Más información sobre PyCaret
| ⭐ Tutoriales | Consulta los tutoriales oficiales. |
|---|---|
| 📋 C uadernos | Cuadernos de ejemplo creados por la comunidad. |
| 📙 Blog | Tutoriales y artículos de colaboradores. |
| 📚 Documentación | La documentación detallada de la API de PyCaret |
| 📺 Videotutoriales | Vídeo tutorial de PyCaret de varios eventos. |
Conclusión
La previsión de series temporales es una habilidad muy útil de aprender. Muchos problemas de la vida real son de naturaleza temporal. La previsión tiene una serie de aplicaciones en diversos sectores, con toneladas de aplicaciones prácticas, como: previsión meteorológica, previsión económica, previsión sanitaria, previsión financiera, previsión comercial, previsión empresarial, estudios medioambientales, estudios sociales, etc.
Básicamente, cualquier dato histórico con intervalos coherentes puede analizarse con métodos de análisis de series temporales que conducen a una tarea de previsión que aprende de los datos históricos e intenta predecir el futuro. Para concluir, existen tres grandes categorías para la previsión de series temporales:
- Modelos estadísticos - Alisamiento exponencial, ARIMA, SARIMA, TBATS, etc.
- Machine Learning -Linear Regression, XGBoost, Random Forest, etc.
- Aprendizaje profundo - RNN, LSTM
Si quieres ampliar tus conocimientos y habilidades en la previsión de series temporales, echa un vistazo a este increíble tema de "Series temporales con Python" de Datacamp. En este tema, aprenderás a manipular datos de series temporales con pandas, a trabajar con bibliotecas estadísticas como NumPy y statsmodels para analizar datos, y a desarrollar tus habilidades de visualización con Matplotlib, SciPy y seaborn. Al final de este tema, sabrás cómo predecir el futuro utilizando modelos de clase ARIMA y generar predicciones y perspectivas utilizando modelos de aprendizaje automático.