Les données chronologiques sont des données collectées sur le même sujet à différents moments, comme le PIB d'un pays par année, le cours de l'action d'une société particulière sur une période donnée ou les battements de votre cœur enregistrés à chaque seconde. Toutes les données que vous pouvez saisir en continu à différents intervalles de temps constituent une forme de série chronologique.
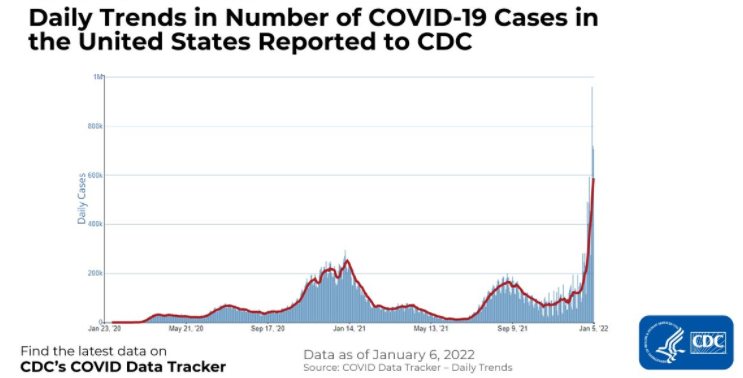
Vous trouverez ci-dessous un exemple de données chronologiques montrant le nombre de cas de COVID-19 aux États-Unis, tels qu'ils ont été signalés aux CDC. L'axe des abscisses indique le temps qui passe et l'axe des ordonnées représente le nombre de cas COVID-19 en milliers.
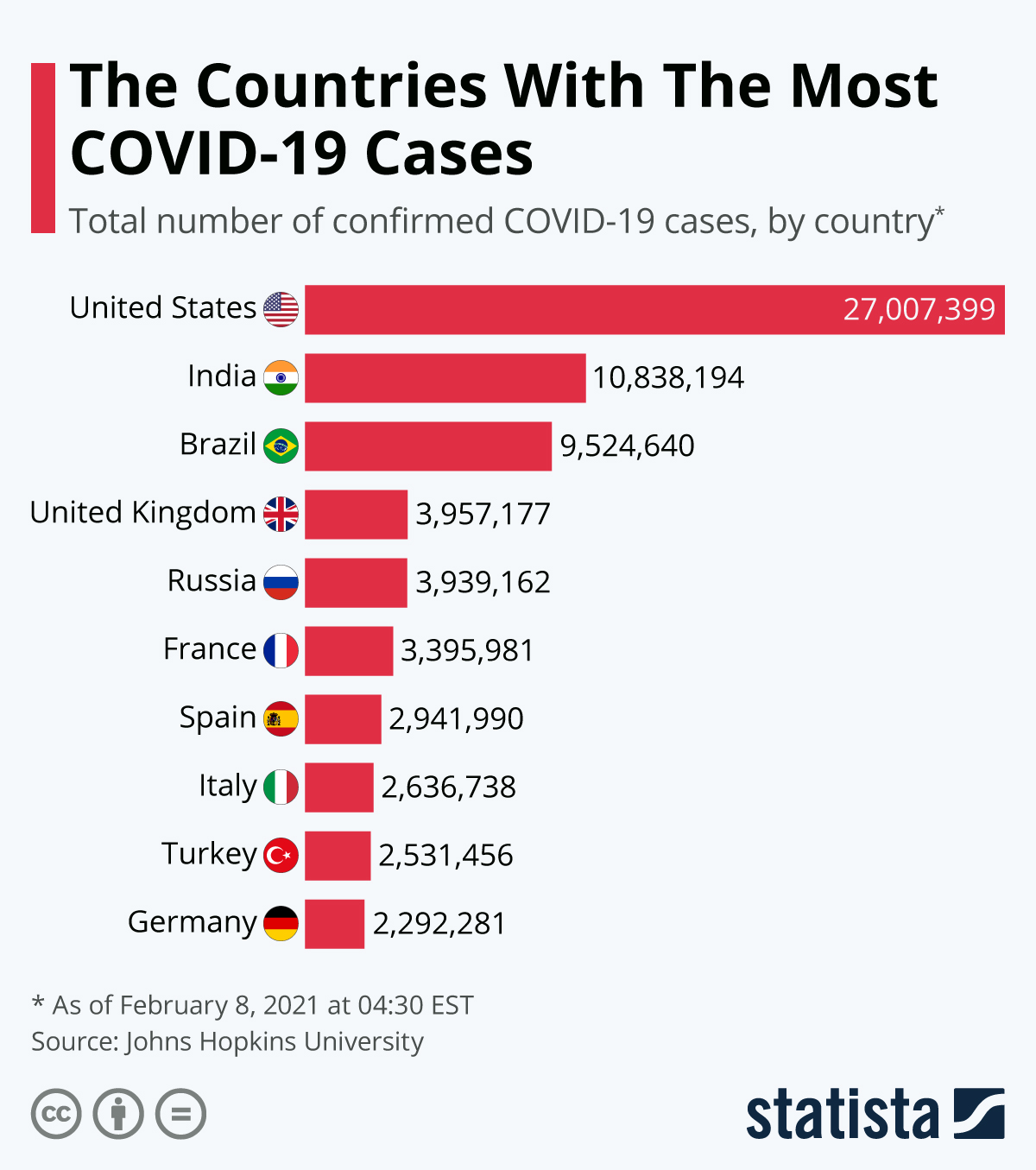
D'autre part, les ensembles de données plus conventionnels qui stockent des informations à un moment donné, telles que des informations sur les clients, les produits, les entreprises, etc. sont appelés données transversales. L'ensemble de données ci-dessous en est un exemple : il s'agit du cursus des pays ayant enregistré le plus grand nombre de cas de COVID-19 au cours d'une période déterminée et cohérente pour tous les pays.
Il n'est pas très difficile de faire la distinction entre les données transversales et les données chronologiques, car les objectifs de l'analyse pour les deux ensembles de données sont très différents. Dans nos exemples, nous nous sommes d'abord intéressés au cursus des cas de COVID-19 sur une période donnée, avant d'analyser les cas de COVID-19 par pays sur une période fixe.
Un ensemble de données réel typique est susceptible d'être un hybride de ces formats. Prenons l'exemple d'un détaillant comme Walmart qui vend des milliers de produits chaque jour. Si vous analysez les ventes par produit un jour donné, il s'agira d'une analyse transversale. Vous pouvez par exemple chercher à savoir quel est l'article le plus vendu la veille de Noël. Par comparaison, si vous souhaitez connaître les ventes d'un article particulier sur une période donnée (disons les cinq dernières années), il s'agira d'une analyse de séries chronologiques.
Les objectifs sont différents selon qu'il s'agit d'analyser des séries temporelles ou des données transversales, et un ensemble de données réelles est susceptible d'être un hybride de séries temporelles et de données transversales.
Qu'est-ce que la prévision des séries temporelles ?
La prévision des séries temporelles est exactement ce qu'elle semble être : prédire des valeurs inconnues. La prévision de séries temporelles implique la collecte de données historiques, leur préparation en vue de leur utilisation par des algorithmes, puis la prévision des valeurs futures sur la base de modèles tirés des données historiques.
Il existe de nombreuses raisons pour lesquelles les entreprises peuvent être intéressées par des prévisions de valeurs futures, à savoir le PIB, les ventes mensuelles, les stocks, le chômage et les températures mondiales :
- Un détaillant peut être intéressé par la prévision des ventes futures au niveau d'une UGS (unité de gestion des stocks) à des fins de planification et de budgétisation.
- Un petit commerçant peut être intéressé par la prévision des ventes par magasin, afin de programmer les ressources adéquates (plus de personnel pendant les périodes d'affluence et vice versa).
- Un géant du logiciel comme Google peut être intéressé par la connaissance de l'heure ou du jour le plus chargé de la journée afin de planifier les ressources du serveur en conséquence.
- Les services de santé pourraient être intéressés par la prévision du nombre cumulé de vaccinations COVID administrées afin de pouvoir mieux prévoir le moment où l'immunité collective est censée se mettre en place.
Type de prévision des séries temporelles
Il existe trois types de prévisions de séries temporelles. Le choix dépend du type de données que vous traitez et du cas d'utilisation :
Prévision univariée
Une série temporelle univariée, comme son nom l'indique, est une série comportant une seule variable dépendante du temps. Par exemple, si vous suivez les valeurs de température horaire pour une région donnée et que vous souhaitez prévoir la température future à l'aide des températures historiques, il s'agit d'une prévision de série temporelle univariée. Vos données peuvent ressembler à ceci :
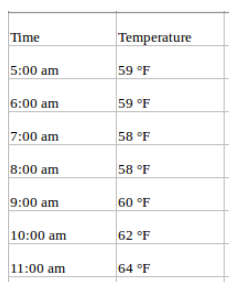
Prévisions multivariées
En revanche, une série temporelle multivariée comporte plus d'une variable dépendant du temps. Chaque variable dépend non seulement de ses valeurs passées, mais aussi d'autres variables. Cette dépendance est utilisée pour prévoir les valeurs futures.
Reprenons l'exemple ci-dessus et supposons que notre ensemble de données comprenne d'autres attributs météorologiques sur la même période, tels que le pourcentage de transpiration, le point de rosée, la vitesse du vent, etc. Dans ce cas, plusieurs variables doivent être prises en compte pour prédire la température de manière optimale. Une telle série entre dans la catégorie des séries temporelles multivariées. Votre jeu de données se présente désormais comme suit :
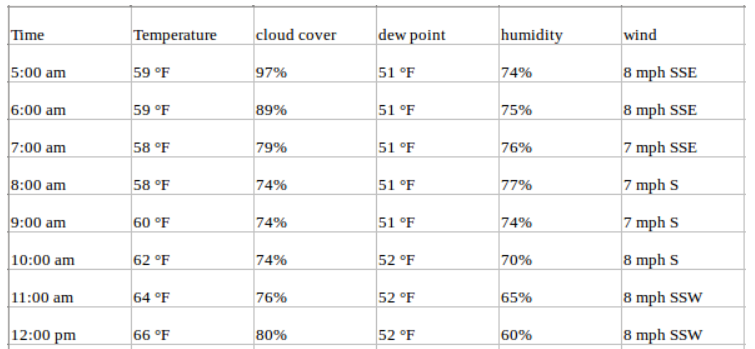
Vous continuez à prévoir les valeurs de température pour l'avenir, mais vous pouvez maintenant utiliser d'autres informations disponibles dans votre prévision, car nous supposons que les valeurs de température dépendront également de ces facteurs.
 Source de l'image : Van Nguyen
Source de l'image : Van Nguyen
Lorsqu'il s'agit de prévisions de séries temporelles multivariées, les variables d'entrée peuvent être de deux types :
- Exogène : Variables d'entrée qui ne sont pas influencées par d'autres variables d'entrée et dont dépend la variable de sortie.
- Endogène : Variables d'entrée qui sont influencées par d'autres variables d'entrée et dont dépend la variable de sortie.
Ce tutoriel aborde plusieurs modèles classiques, mais tous ne permettent pas d'effectuer des prévisions de séries temporelles multivariées. Dans de telles situations, les modèles d'apprentissage automatique viennent à la rescousse, car vous pouvez modéliser n'importe quel problème de prévision de série temporelle avec la régression. Nous en verrons un exemple plus loin dans ce tutoriel.
Méthodes de prévision des séries temporelles
Les prévisions de séries temporelles peuvent être classées dans les catégories suivantes :
- Modèles classiques / statistiques - Moyennes mobiles, lissage exponentiel, ARIMA, SARIMA, TBATS
- Apprentissage automatique - Régression linéaire, XGBoost, Random Forest, ou tout modèle d'apprentissage automatique avec des méthodes de réduction
- Apprentissage profond - RNN, LSTM
Ce tutoriel se concentre sur les deux premières méthodes : les modèles classiques/statistiques et l'apprentissage automatique. Les méthodes d'apprentissage en profondeur ne font pas partie du champ d'application de ce tutoriel.
Modèles statistiques
Lorsqu'il s'agit de prévoir des séries temporelles à l'aide de modèles statistiques, il existe un certain nombre d'algorithmes populaires et bien acceptés. Chacune d'entre elles a des modalités mathématiques différentes et s'accompagne d'un ensemble différent d'hypothèses qui doivent être satisfaites. Ce tutoriel n'approfondira pas les concepts mathématiques, il se contentera de donner une intuition qui, nous l'espérons, vous sera utile.
ARIMA
ARIMA est l'une des méthodes classiques les plus populaires pour la prévision des séries temporelles. Il s'agit d'un type de modèle qui prévoit une série temporelle donnée sur la base de ses propres valeurs passées, c'est-à-dire ses propres retards et les erreurs de prévision retardées. L'ARIMA se compose de trois éléments :
- Autorégression (AR) : désigne un modèle qui montre une variable changeante qui régresse sur ses propres valeurs retardées ou antérieures.
- Intégré (I) : représente la différenciation des observations brutes pour permettre à la série temporelle de devenir stationnaire (c'est-à-dire que les valeurs des données sont remplacées par la différence entre les valeurs des données et les valeurs précédentes).
- Moyenne mobile (MA) : incorpore la dépendance entre une observation et une erreur résiduelle d'un modèle de moyenne mobile appliqué à des observations décalées.
La partie "AR" d'ARIMA indique que la variable évolutive d'intérêt est régressée sur ses propres valeurs retardées (c'est-à-dire observées antérieurement). La partie "MA" indique que l'erreur de régression est en fait une combinaison linéaire de termes d'erreur dont les valeurs se sont produites simultanément et à différents moments dans le passé. Le "I" (pour "intégré") indique que les valeurs des données ont été remplacées par la différence entre leurs valeurs et les valeurs précédentes (et ce processus de différenciation peut avoir été effectué plus d'une fois). L'objectif de chacune de ces caractéristiques est de faire en sorte que le modèle s'adapte le mieux possible aux données.
SARIMA
Une extension de l'ARIMA qui permet la modélisation directe de la composante saisonnière de la série est appelée SARIMA. L'un des problèmes du modèle ARIMA est qu'il ne prend pas en charge les données saisonnières. Il s'agit d'une série chronologique avec un cycle répétitif. ARIMA s'attend à des données qui ne sont pas saisonnières ou dont la composante saisonnière a été supprimée, c'est-à-dire corrigées des variations saisonnières par des méthodes telles que la différenciation saisonnière. SARIMA ajoute trois nouveaux hyperparamètres pour spécifier l'autorégression (AR), la différenciation (I) et la moyenne mobile (MA) pour la composante saisonnière de la série.
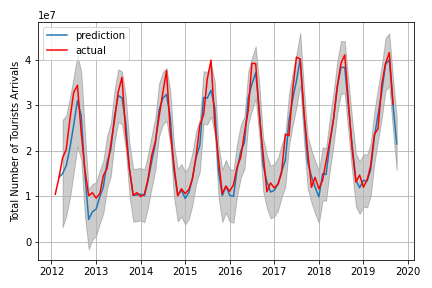 Prévisions à l'aide du modèle SARIMA
Prévisions à l'aide du modèle SARIMA
Lissage exponentiel
Le lissage exponentiel est une méthode de prévision des séries temporelles pour les données univariées. Il peut être étendu pour prendre en charge des données présentant une tendance ou une composante saisonnière. Il peut être utilisé comme alternative à la célèbre famille de modèles ARIMA.
Le lissage exponentiel des données de séries temporelles attribue des pondérations exponentiellement décroissantes aux observations les plus récentes et les plus anciennes. Plus les données sont anciennes, moins elles ont de poids, alors que les données plus récentes ont plus de poids.
- Le lissage exponentiel simple utilise une moyenne mobile pondérée avec des poids décroissants de manière exponentielle.
- Le lissage exponentiel de Holt est généralement plus fiable pour traiter les données qui présentent des tendances.
- Le lissage exponentiel triple (également appelé Holt-Winters multiplicatif) est plus fiable pour les tendances paraboliques ou les données qui présentent des tendances et une saisonnalité.
TBATS
Les modèles TBATS sont destinés aux données de séries temporelles à saisonnalité multiple. Par exemple, les données relatives aux ventes au détail peuvent présenter un schéma quotidien et hebdomadaire, ainsi qu'un schéma annuel.
Dans TBATS, une transformation de Box-Cox est appliquée à la série temporelle originale, puis celle-ci est modélisée comme une combinaison linéaire d'une tendance lissée de manière exponentielle, d'une composante saisonnière et d'une composante ARMA.
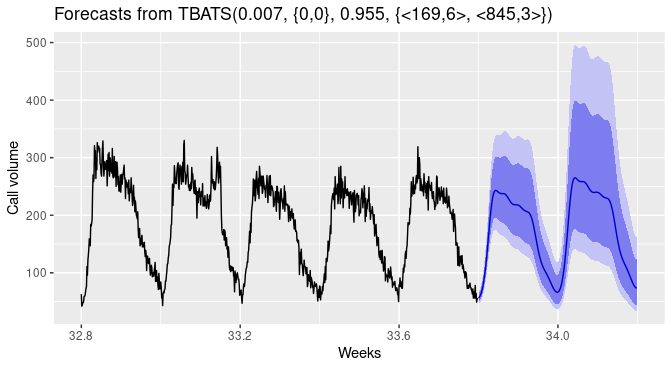 Prévisions à l'aide de TBATS
Prévisions à l'aide de TBATS
Apprentissage automatique
Si vous ne souhaitez pas utiliser de modèles statistiques ou s'ils ne sont pas performants, vous pouvez essayer cette méthode. L'apprentissage automatique est une autre façon de modéliser les données de séries temporelles à des fins de prévision. Dans cette méthode, nous extrayons des caractéristiques de la date pour les ajouter à notre "variable X" et la valeur de la série temporelle est la "variable y". Prenons un exemple :
Pour les besoins de ce tutoriel, j'ai utilisé le jeu de données des passagers des compagnies aériennes américaines disponible en téléchargement sur Kaggle.
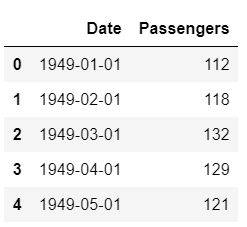 Ensemble de données Échantillon
Ensemble de données Échantillon
Nous pouvons extraire des caractéristiques de la colonne "Date" telles que le mois, l'année, la semaine de l'année, etc. Voir l'exemple :
# extract month and year from dates
data['Month'] = [i.month for i in data['Date']]
data['Year'] = [i.year for i in data['Date']]
# create a sequence of numbers
data['Series'] = np.arange(1,len(data)+1)
# drop unnecessary columns and re-arrange
data.drop(['Date', 'MA12'], axis=1, inplace=True)
data = data[['Series', 'Year', 'Month', 'Passengers']]
# check the head of the dataset
data.head()
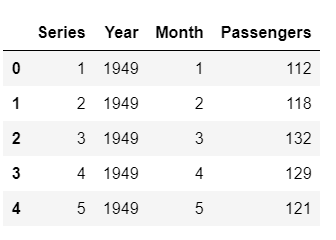 Échantillon de lignes après l'extraction des caractéristiques
Échantillon de lignes après l'extraction des caractéristiques
Il convient de noter ici que la répartition formation-test pour les données de séries temporelles est particulière. Comme vous ne pouvez pas modifier l'ordre du tableau, vous devez vous assurer que vous n'échantillonnez pas au hasard, car vous voulez que vos données de test contiennent des points qui se situent dans le futur par rapport aux points des données de train (le temps avance toujours).
# split data into train-test set
train = data[data['Year'] < 1960]
test = data[data['Year'] >= 1960]
# check shape
train.shape, test.shape
>>> ((132, 4), (12, 4))
Maintenant que nous avons effectué la répartition formation-test-séparation, nous sommes prêts à former un modèle d'apprentissage automatique sur les données de formation, à le noter sur les données de test et à évaluer les performances de notre modèle. Dans cet exemple, j'utiliserai PyCaret ; une bibliothèque d'apprentissage automatique open-source et low-code en Python qui automatise les flux de travail d'apprentissage automatique. Pour utiliser PyCaret, vous devez l'installer à l'aide de pip.
# install pycaret
pip install pycaret
Si vous avez besoin d'aide pendant l'installation, veuillez vous référer à la documentation officielle.
En supposant que vous avez installé PyCaret avec succès :
# import the regression module
from pycaret.regression import *
# initialize setup
s = setup(data = train, test_data = test, target = 'Passengers', fold_strategy = 'timeseries', numeric_features = ['Year', 'Series'], fold = 3, transform_target = True, session_id = 123)
Pour entraîner des modèles d'apprentissage automatique, vous n'avez plus qu'à exécuter une ligne :
best = compare_models(sort = 'MAE')
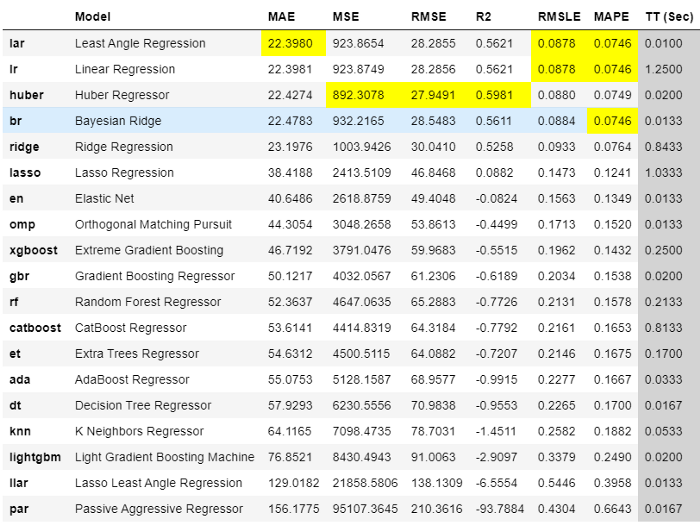 Résultat de la comparaison des modèles
Résultat de la comparaison des modèles
Le meilleur modèle utilisant la validation croisée 3 fois basée sur l'erreur absolue moyenne (MAE) est la régression de l'angle loué. Nous pouvons maintenant utiliser ce modèle pour prévoir l'avenir. Pour cela, nous devons créer des "variables X" dans le futur. Pour ce faire, vous pouvez créer des dates futures et en extraire des caractéristiques.
Puisque nous avons entraîné notre modèle sur les données jusqu'en 1960, faisons des prévisions pour les cinq années à venir, jusqu'en 1965. Pour utiliser notre modèle final afin de générer des prédictions futures, nous devons d'abord créer un ensemble de données composé des colonnes Mois, Année, Série sur les dates futures. Le code ci-dessous crée le futur ensemble de données "X".
future_dates = pd.date_range(start = '1961-01-01', end = '1965-01-01', freq = 'MS')
future_df = pd.DataFrame()
future_df['Month'] = [i.month for i in future_dates]
future_df['Year'] = [i.year for i in future_dates]
future_df['Series'] = np.arange(145,(145+len(future_dates)))
future_df.head()
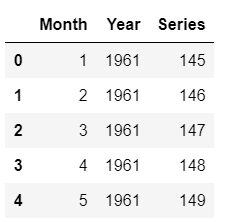 Echantillon de lignes de future_df
Echantillon de lignes de future_df
Nous pouvons maintenant utiliser future_df pour faire des prédictions :
predictions_future = predict_model(best, data=future_df)
predictions_future.head()
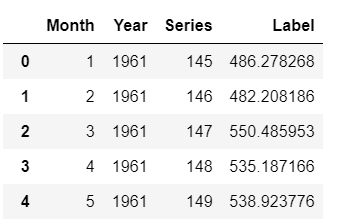 Sortie de predictions_future.head()
Sortie de predictions_future.head()
Et maintenant, nous pouvons le tracer :
concat_df = pd.concat([data,predictions_future], axis=0)
concat_df_i = pd.date_range(start='1949-01-01', end = '1965-01-01', freq = 'MS')
concat_df.set_index(concat_df_i, inplace=True)
fig = px.line(concat_df, x=concat_df.index, y=["Passengers", "Label"], template = 'plotly_dark')
fig.show()
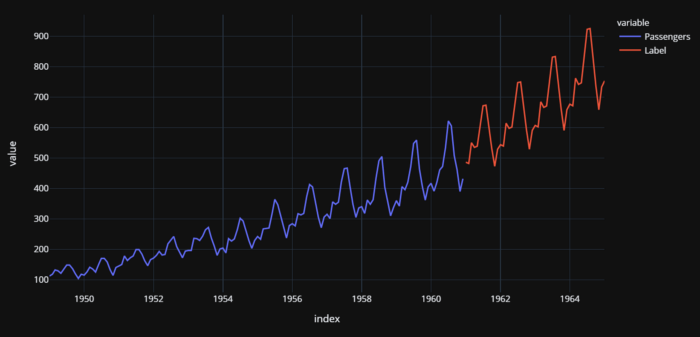 Nombre réel (1949-1960) et prévisionnel (1961-1964) de passagers des compagnies aériennes américaines
Nombre réel (1949-1960) et prévisionnel (1961-1964) de passagers des compagnies aériennes américaines
Il y a quelques éléments importants à noter ici. Lorsque vous traitez des séries temporelles univariées, vous pouvez toujours les convertir en problèmes de régression et les résoudre comme dans cet exemple. Cependant, vous devez être prudent en ce qui concerne la validation croisée. Vous ne pouvez pas effectuer de validation croisée aléatoire sur les modèles de séries temporelles et vous devez utiliser des techniques appropriées aux séries temporelles. Dans cet exemple, PyCaret utilise TimeSeriesSplit de la bibliothèque scikit-learn.
Cadres Python pour les prévisions
Facebook Prophète
Prophet est un logiciel libre publié par l'équipe Core Data Science de Facebook. Il est disponible en téléchargement sur CRAN et PyPI.
Prophet est une procédure de prévision des données de séries temporelles basée sur un modèle additif où les tendances non linéaires sont adaptées à la saisonnalité annuelle, hebdomadaire et quotidienne, ainsi qu'aux effets des vacances. Il fonctionne mieux avec les séries temporelles qui ont de forts effets saisonniers et plusieurs saisons de données historiques. Prophet est robuste aux données manquantes et aux changements de tendance, et traite généralement bien les valeurs aberrantes.
Pour en savoir plus, consultez ce lien.
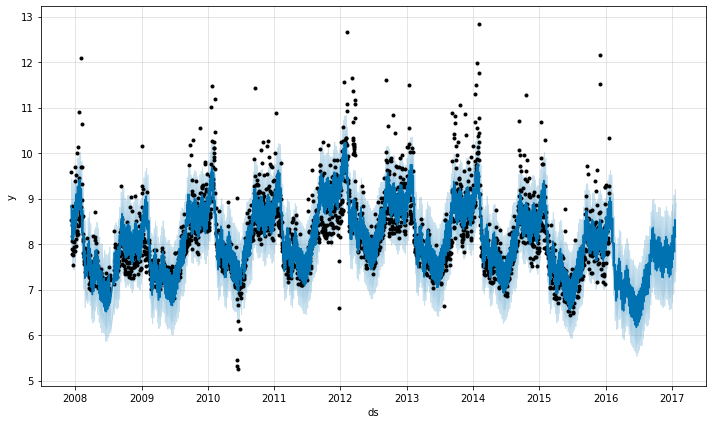 Prévisions à l'aide de FB Prophet
Prévisions à l'aide de FB Prophet
sktime
sktime est un cadre unifié et open-source pour l'apprentissage automatique des séries temporelles. Il fournit une plateforme facile à utiliser, flexible et modulaire pour un large éventail de tâches d'apprentissage automatique des séries temporelles. Il offre des interfaces compatibles avec scikit-learn et des outils de composition de modèles, dans le but de rendre l'écosystème plus utilisable et interopérable dans son ensemble.
 Pour en savoir plus sur sktime, consultez ce lien.
Pour en savoir plus sur sktime, consultez ce lien.
pmdarima
Pmdarima est une bibliothèque statistique conçue pour combler le vide dans les capacités d'analyse de séries temporelles de Python. Il s'agit notamment de
- L'équivalent de la fonctionnalité auto.arima de R
- Une collection de tests statistiques de stationnarité et de saisonnalité
- Décompositions de séries temporelles saisonnières
- Utilitaires de validation croisée
- Une riche collection d'ensembles de données de séries temporelles intégrées pour le prototypage et les exemples.
Pour en savoir plus sur pmdarima, consultez cette page.
Kats
Kats est un autre projet open-source extraordinaire de Facebook, lancé par l'équipe Data Science de l'infrastructure. Il peut être téléchargé sur PyPI.
Kats est une boîte à outils pour l'analyse des données de séries temporelles ; un cadre léger, facile à utiliser et généralisable pour effectuer des analyses de séries temporelles. Kats vise à fournir un guichet unique pour l'analyse des séries temporelles, y compris la détection, la prévision, l'extraction et l'incorporation de caractéristiques, l'analyse multivariée, etc.
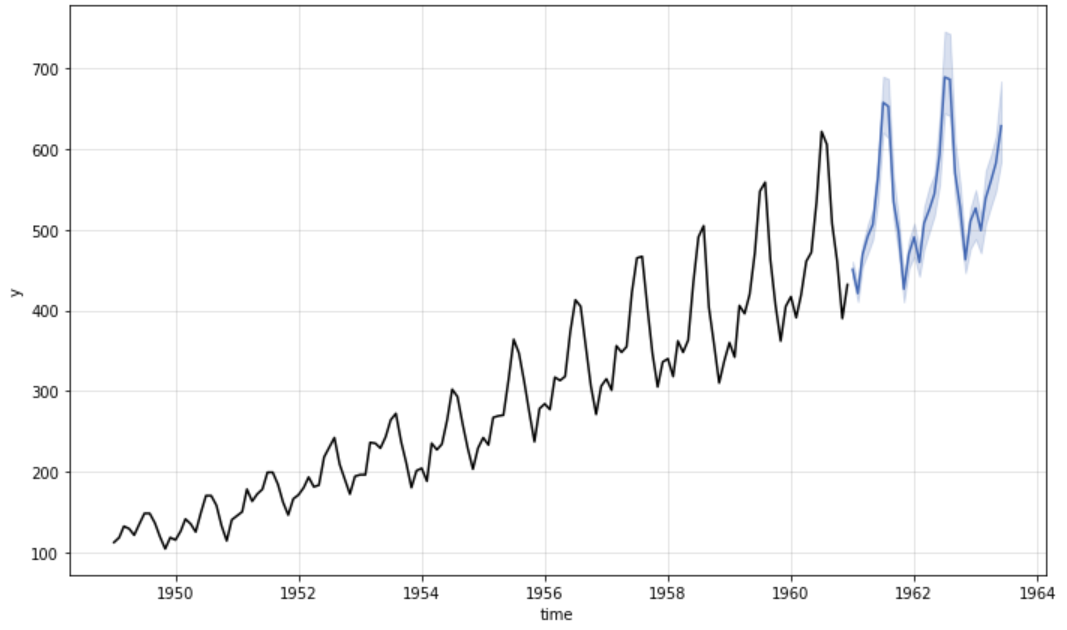 Prévisions à l'aide de KATS
Prévisions à l'aide de KATS
Pour en savoir plus sur KATS, consultez ce lien.
Orbite
Orbit est un étonnant projet open-source d'Uber. Il s'agit d'une bibliothèque Python pour la prévision bayésienne des séries temporelles. Il fournit une interface familière et intuitive d'initialisation et de prédiction pour les tâches liées aux séries temporelles, tout en utilisant des langages de programmation probabilistes sous le capot.
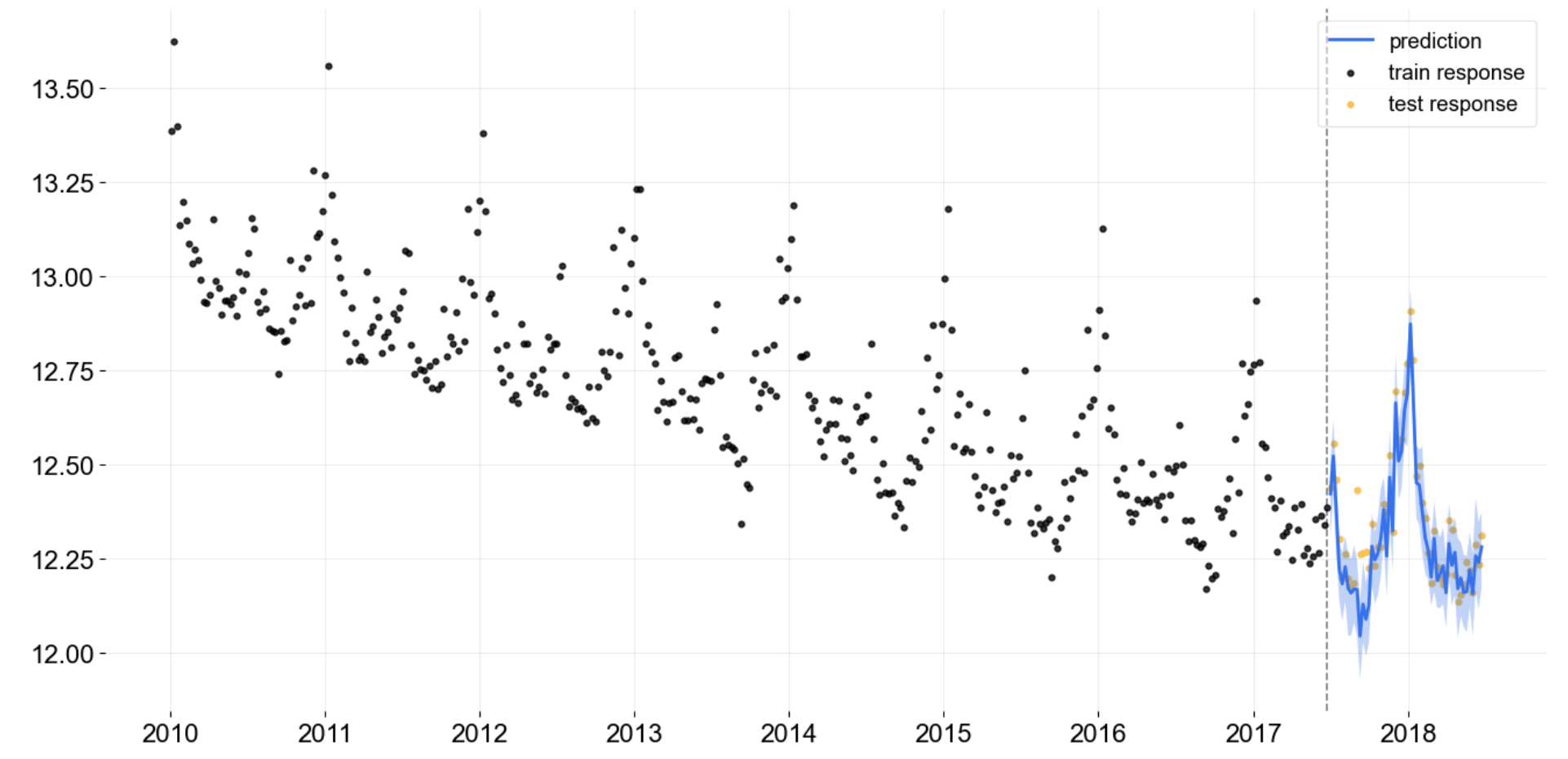 Prévisions à l'aide de l'orbite
Prévisions à l'aide de l'orbite
Pour en savoir plus sur Orbit, consultez ce lien.
PyCaret
PyCaret est une bibliothèque d'apprentissage automatique open-source et low-code en Python qui automatise les flux de travail d'apprentissage automatique. Avec PyCaret, vous passez moins de temps à coder et plus de temps à analyser. Vous pouvez entraîner votre modèle, l'analyser, itérer plus rapidement que jamais et le déployer instantanément en tant qu'API REST ou même construire une simple application ML frontale, le tout à partir de votre Notebook préféré.
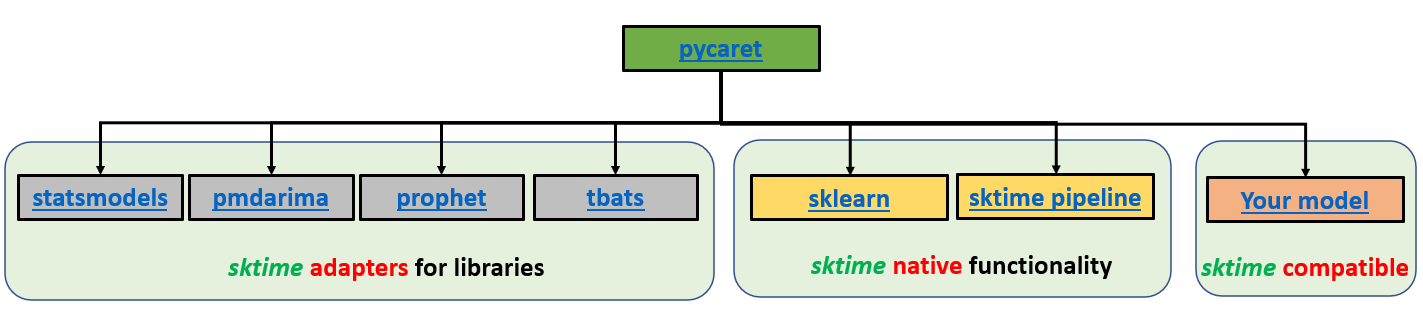 Architecture du module PyCaret Time Series. Développé par le développeur principal Nikhil Gupta.
Architecture du module PyCaret Time Series. Développé par le développeur principal Nikhil Gupta.
Ensuite, nous verrons un exemple de tâche de prévision de séries temporelles de bout en bout à l'aide de la bibliothèque PyCaret.
Exemple de bout en bout
Le module de séries temporelles de PyCaret est disponible en version beta, vous pouvez le télécharger à partir de pip.
pip install pycaret-ts-alpha
Lien vers ce tutoriel sur Colab.
Ensemble de données
Nous avons utilisé ici l'ensemble de données des compagnies aériennes qui est également disponible dans le référentiel de données de PyCaret.
from pycaret.datasets import get_data
data = get_data('airlineer')

data.plot()
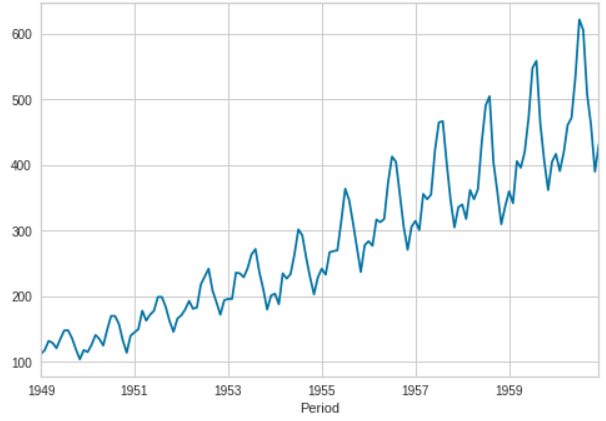
Mise en place de l'expérience
Les expériences dans PyCaret sont lancées à l'aide de la fonction setup. Cette fonction se charge de toutes les étapes de prétraitement, de la répartition formation-test, de la stratégie de validation croisée et de quelques autres tâches.
from pycaret.time_series import *
s = setup(data, session_id = 123)
 Sortie de la fonction Setup
Sortie de la fonction Setup
Analyse exploratoire des données (AED)
Lorsqu'il s'agit de l'EDA de données de séries temporelles univariées, il y a quelques choses que vous pouvez et devez faire.
Pour l'utilisation de modèles classiques et statistiques, vous pouvez effectuer des tests statistiques. Il existe une fonction dans PyCaret qui fait cela pour vous.
check_stats()
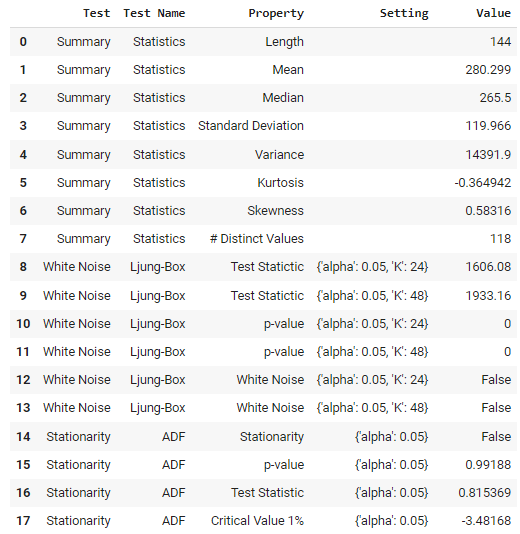 Sortie de la fonction check_stats
Sortie de la fonction check_stats
Si vous avez affaire à des séries temporelles univariées, vous pouvez également les décomposer en composantes de tendance, de saisonnalité et d'erreur pour toute analyse ultérieure.
plot_model(plot = 'decomp_classical")
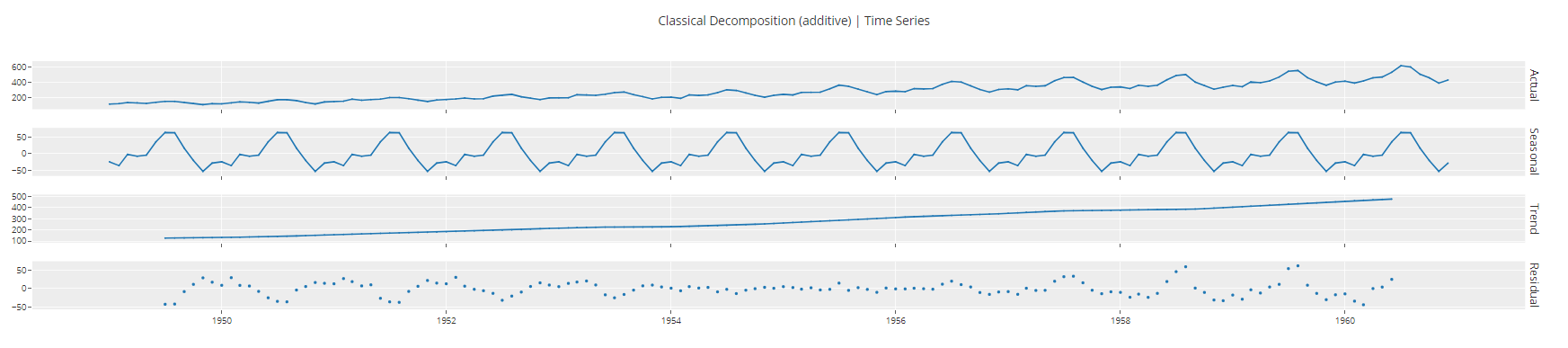 Sortie de la fonction plot_model<c/entre> ## Formation et sélection de modèles ## Pour former plusieurs modèles et en sélectionner un parmi d'autres, nous n'exécutons qu'une seule ligne de code.
Sortie de la fonction plot_model<c/entre> ## Formation et sélection de modèles ## Pour former plusieurs modèles et en sélectionner un parmi d'autres, nous n'exécutons qu'une seule ligne de code. best = compare_models() 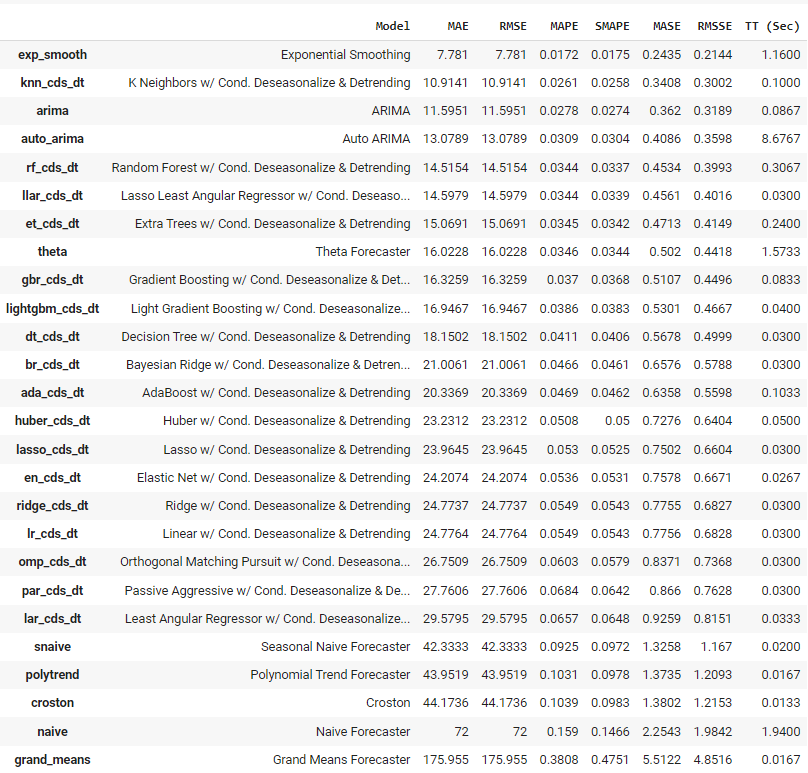 Sortie de la fonction compare_models
Sortie de la fonction compare_models
PyCaret a formé plus de 25 modèles en utilisant la validation croisée appropriée aux séries temporelles et a présenté une liste de modèles par ordre de performance supérieure ou inférieure. Le meilleur modèle basé sur cette expérience pour cet ensemble de données est le lissage exponentiel, avec une erreur absolue moyenne de 7,781.
Analyse du modèle
Avant de déployer ce modèle pour générer des prédictions pour l'avenir, nous pouvons voir quelques graphiques d'analyse pour commenter la qualité de notre modèle.
plot_model(best, plot = 'forecast', data_kwargs = {'fh': 24})
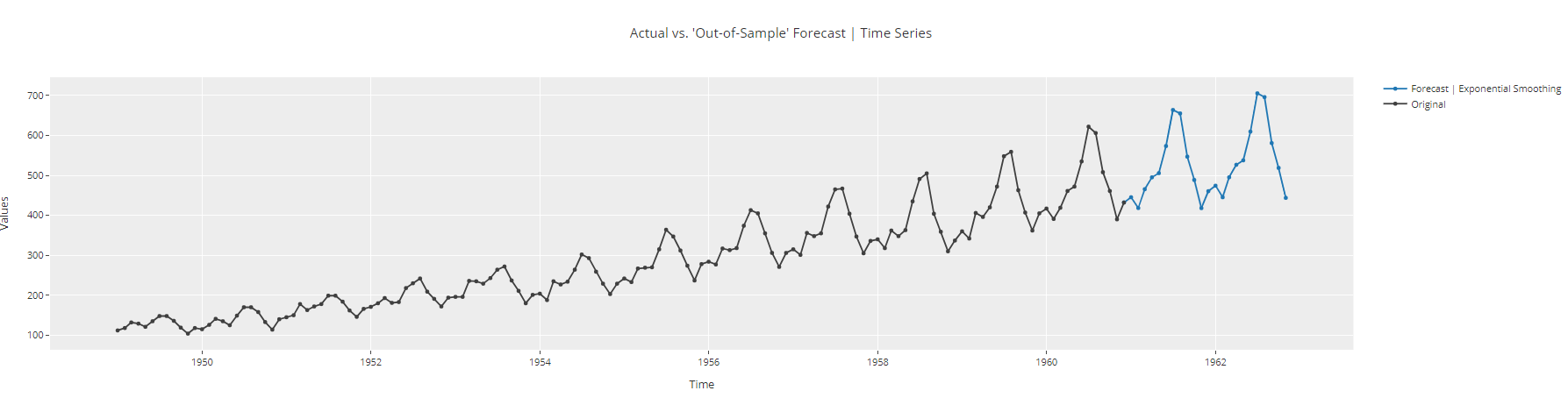 Tracé des prévisions des séries temporelles
Tracé des prévisions des séries temporelles
plot_model(best, plot = 'residuals')
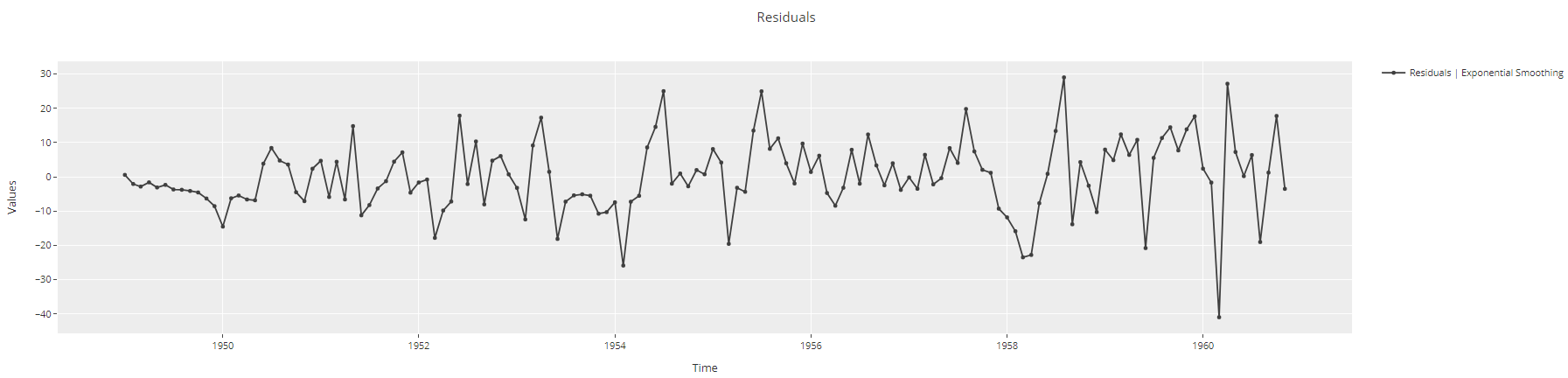 Tracé Tracé des résidus de la série temporelle
Tracé Tracé des résidus de la série temporelle
plot_model(best, plot = 'insample')
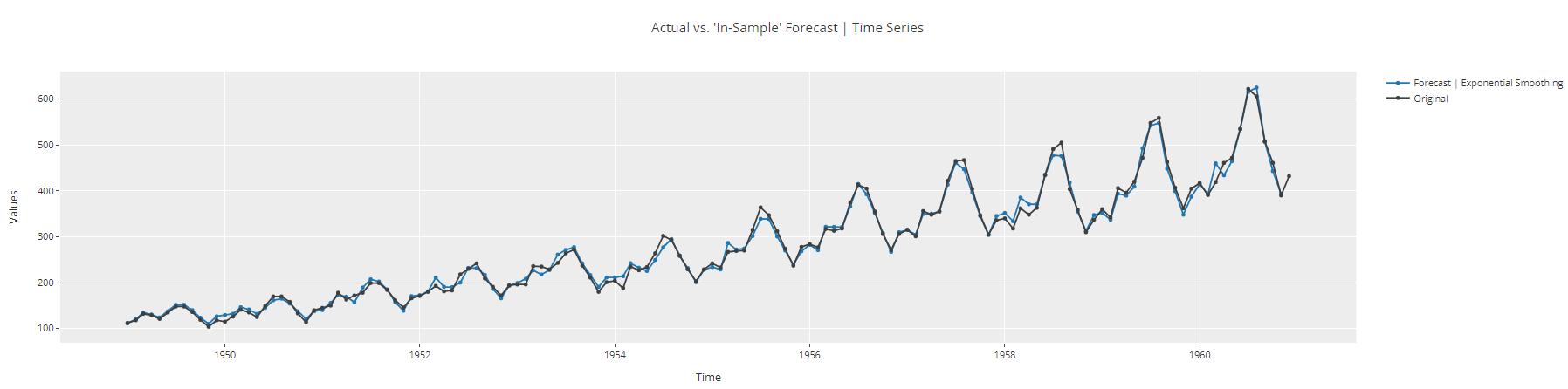 Tracé de l Tracé de l'échantillon de la série temporelle
Tracé de l Tracé de l'échantillon de la série temporelle
Déploiement du modèle
À ce stade, nous sommes prêts à finaliser le modèle et à le sauvegarder pour une utilisation ultérieure.
# finalize model
final_best = finalize_model(best)
# save model
final_best = finalize_model(best)

Pour recharger ce fichier et générer des prédictions sur les données futures :
# load model
loaded_model = load_model('my_best_model')
# generate predictions for the next 48 months
predict_model(loaded_model, fh = 48)
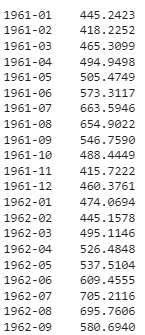 Sortie tronquée
Sortie tronquée
En savoir plus sur PyCaret
| ⭐ Tutoriels | Consultez les tutoriels officiels. |
|---|---|
| 📋 C ahiers | Exemples de carnets créés par la communauté. |
| 📙 Blog | Tutoriels et articles des contributeurs. |
| 📚 Documentation | La documentation détaillée de l'API de PyCaret |
| 📺 Tutoriels vidéo | Tutoriel vidéo de PyCaret à partir de divers événements. |
Conclusion
La prévision des séries temporelles est une compétence très utile à acquérir. De nombreux problèmes de la vie réelle sont de nature temporelle. Les prévisions ont un large éventail d'applications dans divers secteurs, avec des tonnes d'applications pratiques, notamment : les prévisions météorologiques, les prévisions économiques, les prévisions en matière de santé, les prévisions financières, les prévisions en matière de commerce de détail, les prévisions commerciales, les études environnementales, les études sociales, et bien plus encore.
Fondamentalement, toute donnée historique avec des intervalles cohérents peut être analysée avec des méthodes d'analyse de séries temporelles conduisant à une tâche de prévision qui apprend à partir des données historiques et tente de prédire l'avenir. En conclusion, il existe trois grandes catégories de prévisions de séries temporelles :
- Modèles statistiques - Lissage exponentiel, ARIMA, SARIMA, TBATS, etc.
- Apprentissage automatique - Régression linéaire, XGBoost, Random Forest, etc.
- Apprentissage profond - RNN, LSTM
Si vous souhaitez approfondir vos connaissances et vos compétences en matière de prévision des séries temporelles, consultez cette incroyable piste de "Time Series with Python" proposée par DataCamp. Dans ce cursus, vous apprendrez à manipuler des données de séries temporelles à l'aide de pandas, à travailler avec des bibliothèques statistiques, notamment NumPy et statsmodels, pour analyser des données, et à développer vos compétences en matière de visualisation à l'aide de Matplotlib, SciPy et seaborn. À la fin de ce cursus, vous saurez comment prévoir l'avenir à l'aide de modèles de classe ARIMA et générer des prédictions et des connaissances à l'aide de modèles d'apprentissage automatique.