Os dados de séries temporais são dados coletados sobre o mesmo assunto em diferentes momentos, como o PIB de um país por ano, o preço das ações de uma determinada empresa durante um período de tempo ou o seu próprio batimento cardíaco registrado a cada segundo. Qualquer dado que você possa capturar continuamente em diferentes intervalos de tempo é uma forma de dados de série temporal.
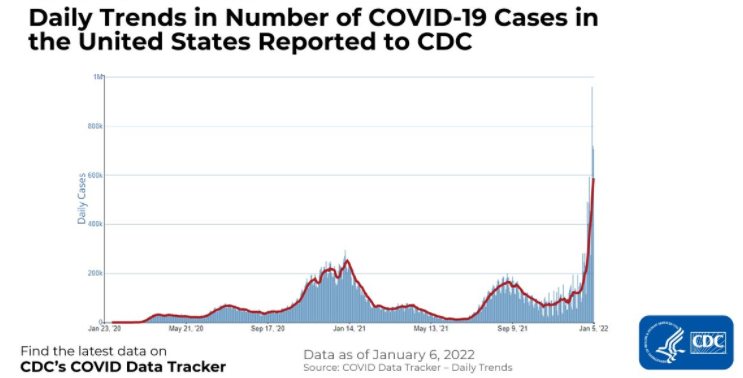
Abaixo você encontra um exemplo de dados de séries temporais que mostram o número de casos de COVID-19 nos Estados Unidos, conforme relatado ao CDC. O eixo x mostra a passagem do tempo e o eixo y representa o número de casos de COVID-19 em milhares.
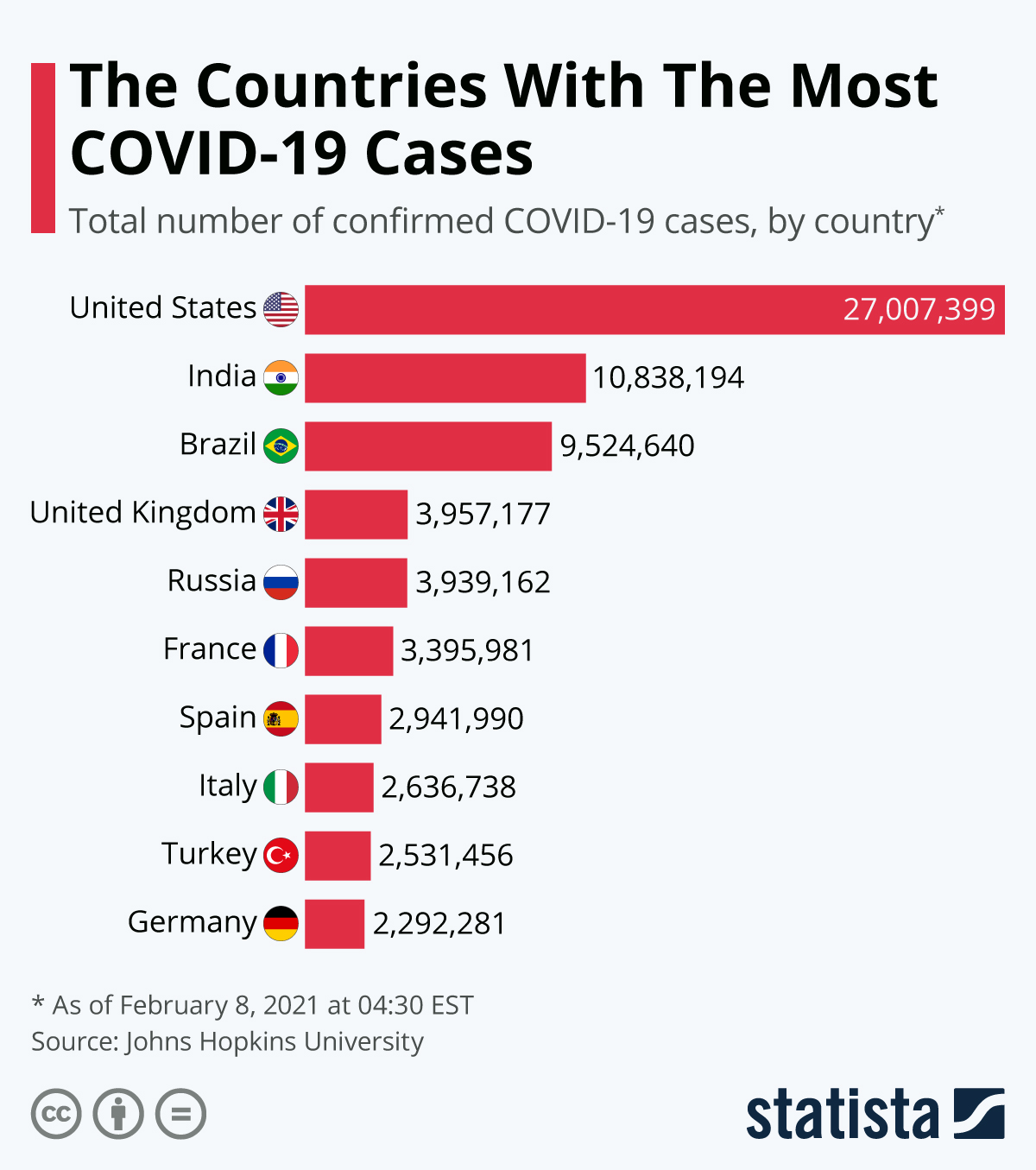
Por outro lado, conjuntos de dados mais convencionais que armazenam informações em um único ponto no tempo, como informações sobre clientes, produtos e empresas, etc., são conhecidos como dados transversais. Um exemplo disso é mostrado no conjunto de dados abaixo, que rastreia os países com o maior número de casos de COVID-19 em um período de tempo fixo e consistente para todos os países.
Não é muito difícil distinguir a diferença entre dados transversais e de séries temporais, pois os objetivos da análise para ambos os conjuntos de dados são muito diferentes. Em nossos exemplos, primeiro estávamos interessados em rastrear os casos de COVID-19 durante um período de tempo, antes de analisar os casos de COVID-19 por país em um período de tempo fixo.
É provável que um conjunto de dados típico do mundo real seja um híbrido desses formatos. Por exemplo, podemos pensar em um varejista como o Walmart, que vende milhares de produtos todos os dias. Se você analisar as vendas por produto em um determinado dia, essa será uma análise transversal. Você pode querer descobrir qual é o item número 1 em vendas na véspera de Natal, por exemplo. Comparativamente, se você quisesse descobrir a venda de um item específico em um período de tempo (digamos, nos últimos 5 anos), essa seria uma análise de série temporal.
Os objetivos são diferentes ao analisar dados de séries temporais e de corte transversal, e um conjunto de dados do mundo real provavelmente será um híbrido de dados de séries temporais e de corte transversal.
O que é previsão de séries temporais?
A previsão de séries temporais é exatamente o que parece: prever valores desconhecidos. A previsão de séries temporais envolve a coleta de dados históricos, preparando-os para serem consumidos por algoritmos e, em seguida, prevendo os valores futuros com base nos padrões aprendidos com os dados históricos.
Há vários motivos pelos quais as empresas podem estar interessadas em prever valores futuros, como PIB, vendas mensais, estoque, desemprego e temperaturas globais:
- Um varejista pode estar interessado em prever vendas futuras em um nível de SKU (unidade de manutenção de estoque) para planejamento e orçamento.
- Um pequeno comerciante pode estar interessado em prever as vendas por loja, para que possa programar os recursos certos (mais pessoas durante os períodos de maior movimento e vice-versa).
- Um gigante do software, como o Google, pode estar interessado em saber qual é a hora mais movimentada do dia ou o dia mais movimentado da semana para que possa programar os recursos do servidor de acordo.
- O departamento de saúde pode estar interessado em prever as vacinações cumulativas contra a COVID-19 administradas para que possa prever melhor quando a imunidade do rebanho deve entrar em ação.
Tipo de previsão de séries temporais
Há três tipos de previsão de séries temporais. Qual deles você deve usar depende do tipo de dados com os quais está lidando e do caso de uso em questão:
Previsão univariada
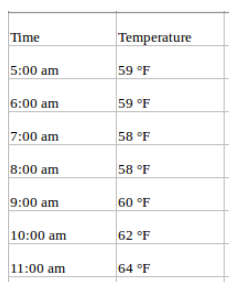
Uma série temporal univariada, como o nome sugere, é uma série com uma única variável dependente do tempo. Por exemplo, se você estiver rastreando valores de temperatura por hora para uma determinada região e quiser prever a temperatura futura usando temperaturas históricas, isso é previsão de série temporal univariada. Seus dados podem ter a seguinte aparência:
Previsão multivariada
Por outro lado, uma série temporal multivariada tem mais de uma variável dependente do tempo. Cada variável depende não apenas de seus valores anteriores, mas também tem alguma dependência de outras variáveis. Essa dependência é usada para prever valores futuros.
Considere o exemplo acima e suponha que nosso conjunto de dados inclua outros atributos relacionados ao clima no mesmo período, como porcentagem de transpiração, ponto de orvalho, velocidade do vento etc., juntamente com os valores de temperatura. Nesse caso, há várias variáveis a serem consideradas para prever a temperatura de forma ideal. Uma série como essa se enquadraria na categoria de série temporal multivariada. Seu conjunto de dados terá a seguinte aparência agora:
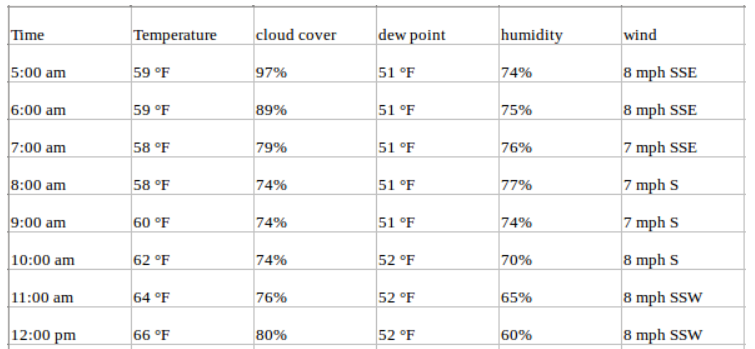
Você ainda está prevendo valores de temperatura para o futuro, mas agora pode usar outras informações disponíveis em sua previsão, pois presumimos que os valores de temperatura também dependerão desses fatores.
 Fonte da imagem: Van Nguyen
Fonte da imagem: Van Nguyen
Quando estamos lidando com previsão de séries temporais multivariadas, as variáveis de entrada podem ser de dois tipos:
- Exógeno: Variáveis de entrada que não são influenciadas por outras variáveis de entrada e das quais depende a variável de saída.
- Endógeno: Variáveis de entrada que são influenciadas por outras variáveis de entrada e das quais depende a variável de saída.
Este tutorial abordará vários modelos clássicos, mas nem todos eles oferecem suporte à previsão de séries temporais multivariadas. Em situações como essas, os modelos de aprendizado de máquina vêm em socorro, pois você pode modelar qualquer problema de previsão de série temporal com regressão. Veremos um exemplo disso mais adiante neste tutorial.
Métodos de previsão de séries temporais
A previsão de séries temporais pode ser classificada nas seguintes categorias:
- Modelos clássicos/estatísticos - médias móveis, suavização exponencial, ARIMA, SARIMA, TBATS
- Aprendizado de máquina - Regressão linear, XGBoost, Random Forest ou qualquer modelo de ML com métodos de redução
- Aprendizagem profunda - RNN, LSTM
Este tutorial se concentra nos dois primeiros métodos: modelos clássicos/estatísticos e aprendizado de máquina. Os métodos de aprendizagem profunda estão fora do escopo deste tutorial.
Modelos estatísticos
Quando se trata de previsão de séries temporais usando modelos estatísticos, há vários algoritmos populares e bem aceitos. Cada um deles tem modalidades matemáticas diferentes e vêm com um conjunto diferente de suposições que devem ser satisfeitas. Este tutorial não se aprofundará nos conceitos matemáticos, mas apenas fornecerá uma intuição que, esperamos, seja útil para você.
ARIMA
O ARIMA é um dos métodos clássicos mais populares para previsão de séries temporais. Significa média móvel integrada autorregressiva e é um tipo de modelo que prevê uma determinada série temporal com base em seus próprios valores passados, ou seja, suas próprias defasagens e os erros de previsão defasados. O ARIMA consiste em três componentes:
- Autoregressão (AR): refere-se a um modelo que mostra uma variável variável variável que regride em seus próprios valores defasados ou anteriores.
- Integrado (I): representa a diferença das observações brutas para permitir que a série temporal se torne estacionária (ou seja, os valores dos dados são substituídos pela diferença entre os valores dos dados e os valores anteriores).
- Média móvel (MA): incorpora a dependência entre uma observação e um erro residual de um modelo de média móvel aplicado a observações defasadas.
A parte "AR" do ARIMA indica que a variável de interesse em evolução é regredida em seus próprios valores defasados (ou seja, observados anteriormente). A parte "MA" indica que o erro da regressão é, na verdade, uma combinação linear de termos de erro cujos valores ocorreram contemporaneamente e em vários momentos no passado. O "I" (de "integrado") indica que os valores dos dados foram substituídos pela diferença entre seus valores e os valores anteriores (e esse processo de diferença pode ter sido realizado mais de uma vez). O objetivo de cada um desses recursos é fazer com que o modelo se ajuste aos dados da melhor forma possível.
SARIMA
Uma extensão do ARIMA que suporta a modelagem direta do componente sazonal da série é chamada SARIMA. Um problema com o modelo ARIMA é que ele não é compatível com dados sazonais. Essa é uma série temporal com um ciclo de repetição. O ARIMA espera dados que não sejam sazonais ou que tenham o componente sazonal removido, por exemplo, ajustados sazonalmente por meio de métodos como a diferenciação sazonal. O SARIMA acrescenta três novos hiperparâmetros para especificar a autorregressão (AR), a diferenciação (I) e a média móvel (MA) para o componente sazonal da série.
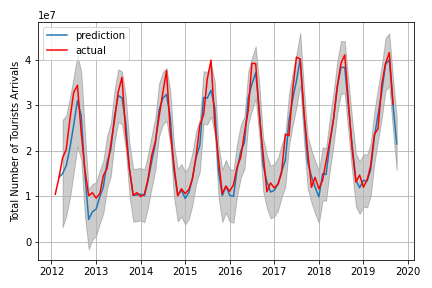 usando Previsão usando o modelo SARIMA
usando Previsão usando o modelo SARIMA
Suavização exponencial
A suavização exponencial é um método de previsão de séries temporais para dados univariados. Ele pode ser estendido para suportar dados com uma tendência ou componente sazonal. Ele pode ser usado como uma alternativa à popular família de modelos ARIMA.
A suavização exponencial de dados de séries temporais atribui pesos exponencialmente decrescentes das observações mais recentes para as mais antigas. Quanto mais antigos os dados, menos peso é dado a eles, enquanto os dados mais recentes recebem mais peso
- A suavização exponencial simples (única) usa uma média móvel ponderada com pesos exponencialmente decrescentes.
- A suavização exponencial de Holt geralmente é mais confiável para lidar com dados que mostram tendências.
- A suavização exponencial tripla (também chamada de Holt-Winters multiplicativa) é mais confiável para tendências parabólicas ou dados que mostram tendências e sazonalidade.
TBATS
Os modelos TBATS são para dados de séries temporais com várias sazonalidades. Por exemplo, os dados de vendas no varejo podem ter um padrão diário e um padrão semanal, bem como um padrão anual.
No TBATS, uma transformação Box-Cox é aplicada à série temporal original e, em seguida, ela é modelada como uma combinação linear de uma tendência exponencialmente suavizada, um componente sazonal e um componente ARMA.
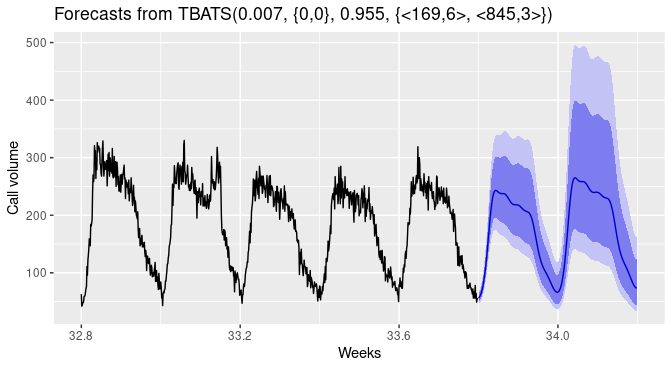 usando Previsão usando a TBATS
usando Previsão usando a TBATS
Aprendizado de máquina
Se não quiser usar modelos estatísticos ou se eles não estiverem funcionando bem, você pode tentar este método. O aprendizado de máquina é uma forma alternativa de modelar dados de séries temporais para previsão. Nesse método, extraímos recursos da data para adicionar à nossa "variável X" e o valor da série temporal é a "variável y". Vamos ver um exemplo:
Para fins deste tutorial, usei o conjunto de dados de passageiros de companhias aéreas dos EUA disponível para download no Kaggle.
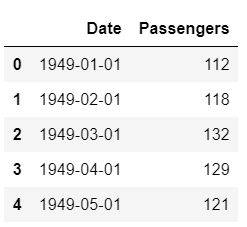 Amostra de conjunto de dados
Amostra de conjunto de dados
Podemos extrair recursos da coluna "Date", como mês, ano, semana do ano etc. Veja um exemplo:
# extract month and year from dates
data['Month'] = [i.month for i in data['Date']]
data['Year'] = [i.year for i in data['Date']]
# create a sequence of numbers
data['Series'] = np.arange(1,len(data)+1)
# drop unnecessary columns and re-arrange
data.drop(['Date', 'MA12'], axis=1, inplace=True)
data = data[['Series', 'Year', 'Month', 'Passengers']]
# check the head of the dataset
data.head()
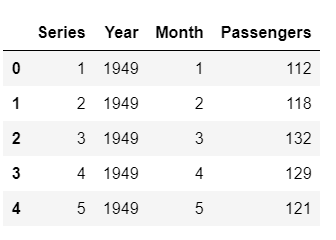 Linhas de amostragem após a extração de recursos
Linhas de amostragem após a extração de recursos
É importante observar que a divisão de treinamento-teste para dados de séries temporais é especial. Como não é possível alterar a ordem da tabela, você precisa garantir que a amostra não seja aleatória, pois deseja que os dados de teste contenham pontos que estão no futuro dos pontos nos dados do trem (o tempo sempre avança).
# split data into train-test set
train = data[data['Year'] < 1960]
test = data[data['Year'] >= 1960]
# check shape
train.shape, test.shape
>>> ((132, 4), (12, 4))
Agora que fizemos a divisão entre treinamento e teste, estamos prontos para treinar um modelo de aprendizado de máquina nos dados de treinamento, pontuá-lo nos dados de teste e avaliar o desempenho do nosso modelo. Neste exemplo, usarei o PyCaret, uma biblioteca de aprendizado de máquina de código aberto e de baixo código em Python que automatiza os fluxos de trabalho de aprendizado de máquina. Para usar o PyCaret, você precisa instalá-lo usando o pip.
# install pycaret
pip install pycaret
Se você precisar de ajuda durante a instalação, consulte a documentação oficial.
Supondo que você tenha instalado o PyCaret com êxito:
# import the regression module
from pycaret.regression import *
# initialize setup
s = setup(data = train, test_data = test, target = 'Passengers', fold_strategy = 'timeseries', numeric_features = ['Year', 'Series'], fold = 3, transform_target = True, session_id = 123)
Agora, para treinar modelos de aprendizado de máquina, você só precisa executar uma linha:
best = compare_models(sort = 'MAE')
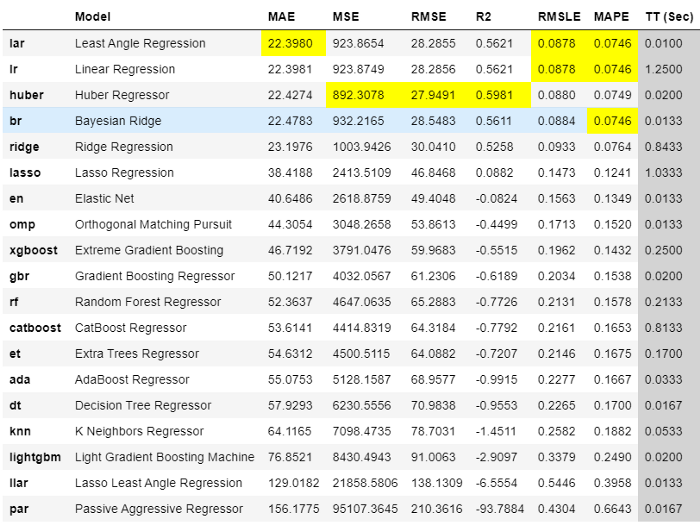 Saída de compare_models
Saída de compare_models
O melhor modelo usando a validação cruzada de três vezes com base no erro médio absoluto (MAE) é a regressão de ângulo alugado. Agora podemos usar esse modelo para prever o futuro. Para isso, temos que criar "X variáveis" no futuro. Isso pode ser feito criando datas futuras e extraindo recursos delas.
Como treinamos nosso modelo nos dados até 1960, vamos fazer uma previsão de cinco anos no futuro, até 1965. Para usar nosso modelo final para gerar previsões futuras, primeiro precisamos criar um conjunto de dados que consiste na coluna Month, Year, Series nas datas futuras. O código abaixo cria o futuro conjunto de dados "X".
future_dates = pd.date_range(start = '1961-01-01', end = '1965-01-01', freq = 'MS')
future_df = pd.DataFrame()
future_df['Month'] = [i.month for i in future_dates]
future_df['Year'] = [i.year for i in future_dates]
future_df['Series'] = np.arange(145,(145+len(future_dates)))
future_df.head()
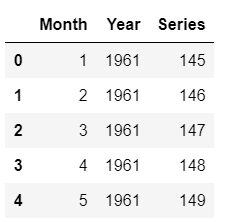 Linhas de amostra de future_df
Linhas de amostra de future_df
Agora podemos usar o future_df para fazer previsões:
predictions_future = predict_model(best, data=future_df)
predictions_future.head()
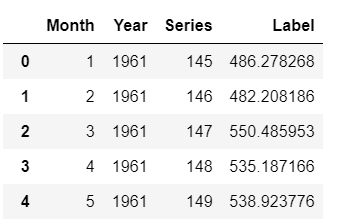 Saída de predictions_future.head()
Saída de predictions_future.head()
E agora podemos traçá-lo:
concat_df = pd.concat([data,predictions_future], axis=0)
concat_df_i = pd.date_range(start='1949-01-01', end = '1965-01-01', freq = 'MS')
concat_df.set_index(concat_df_i, inplace=True)
fig = px.line(concat_df, x=concat_df.index, y=["Passengers", "Label"], template = 'plotly_dark')
fig.show()
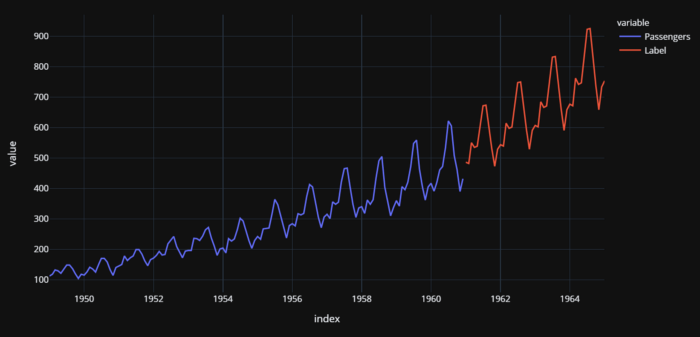 Passageiros reais (1949-1960) e previstos (1961-1964) de companhias aéreas dos EUA
Passageiros reais (1949-1960) e previstos (1961-1964) de companhias aéreas dos EUA
Há alguns elementos importantes a serem observados aqui. Sempre que estiver lidando com séries temporais univariadas, você sempre poderá convertê-las em problemas de regressão e resolvê-las como neste exemplo. No entanto, você precisa ter cuidado com a validação cruzada. Você não pode fazer validação cruzada aleatória em modelos de séries temporais e deve usar técnicas apropriadas para séries temporais. Neste exemplo, o PyCaret usa o TimeSeriesSplit da biblioteca scikit-learn.
Estruturas Python para previsão
Facebook Prophet
O Prophet é um software de código aberto lançado pela equipe de ciência de dados principais do Facebook. Ele está disponível para download no CRAN e no PyPI.
O Prophet é um procedimento de previsão de dados de séries temporais baseado em um modelo aditivo em que as tendências não lineares são ajustadas com sazonalidade anual, semanal e diária, além de efeitos de feriados. Funciona melhor com séries temporais que têm fortes efeitos sazonais e várias temporadas de dados históricos. O Prophet é robusto em relação a dados ausentes e mudanças na tendência, e normalmente lida bem com valores discrepantes.
Para saber mais sobre isso, confira este link.
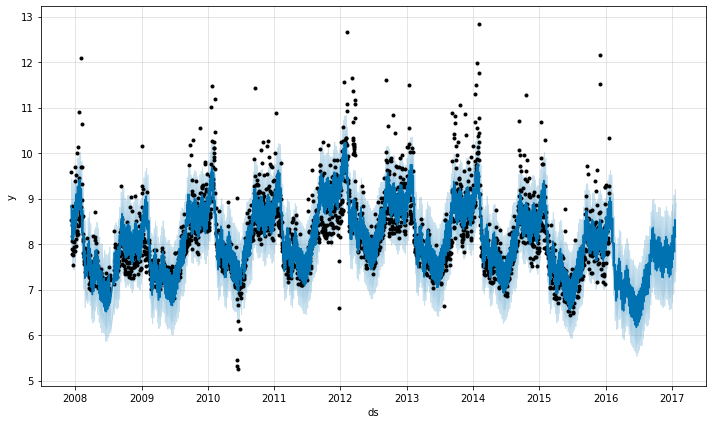 usando Previsão usando o FB Prophet
usando Previsão usando o FB Prophet
sktime
O sktime é uma estrutura unificada e de código aberto para aprendizado de máquina com séries temporais. Ele oferece uma plataforma fácil de usar, flexível e modular para uma ampla gama de tarefas de aprendizado de máquina de séries temporais. Ele oferece interfaces compatíveis com o scikit-learn e ferramentas de composição de modelos, com o objetivo de tornar o ecossistema mais utilizável e interoperável como um todo.
 Para saber mais sobre o sktime, confira este link.
Para saber mais sobre o sktime, confira este link.
pmdarima
Pmdarima é uma biblioteca estatística projetada para preencher a lacuna nos recursos de análise de séries temporais do Python. Isso inclui:
- O equivalente à funcionalidade auto.arima do R
- Uma coleção de testes estatísticos de estacionariedade e sazonalidade
- Decomposições sazonais de séries temporais
- Utilitários de validação cruzada
- Uma rica coleção de conjuntos de dados de séries temporais incorporados para prototipagem e exemplos
Para saber mais sobre o pmdarima, confira esta página.
Kats
O Kats é outro incrível projeto de código aberto do Facebook, lançado pela equipe de ciência de dados de infraestrutura. Ele está disponível para download no PyPI.
O Kats é um kit de ferramentas para analisar dados de séries temporais; uma estrutura leve, fácil de usar e generalizável para realizar análises de séries temporais. O objetivo do Kats é oferecer uma solução completa para análise de séries temporais, incluindo detecção, previsão, extração/incorporação de recursos e análise multivariada, etc.
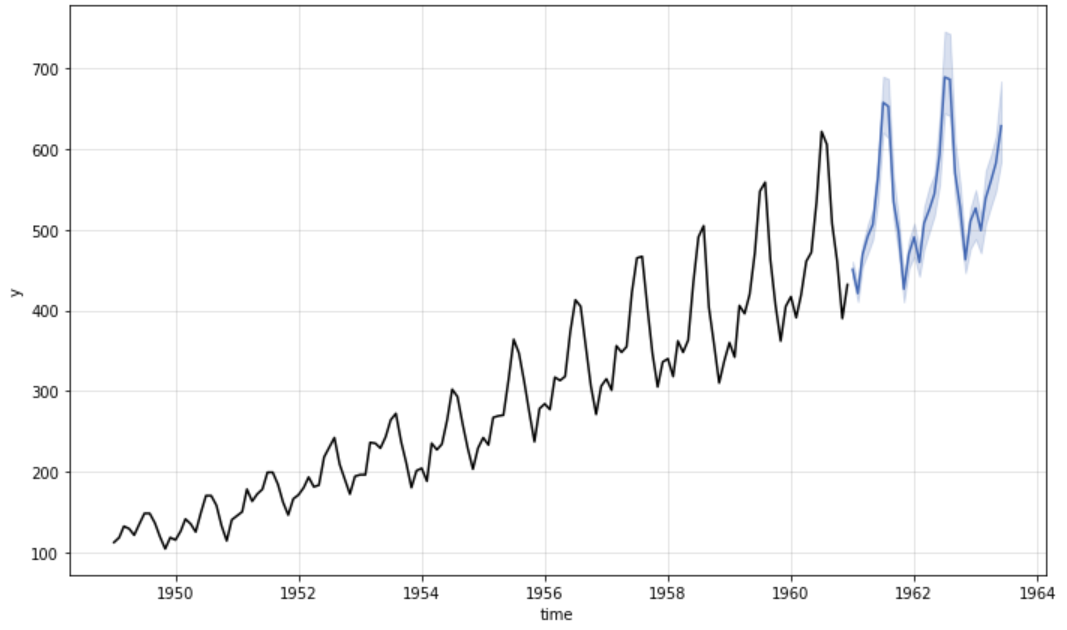 usando Previsão usando o KATS
usando Previsão usando o KATS
Para saber mais sobre o KATS, acesse este link.
Órbita
O Orbit é um incrível projeto de código aberto da Uber. É uma biblioteca Python para previsão de séries temporais bayesianas. Ele oferece uma interface familiar e intuitiva de inicialização e previsão para tarefas de séries temporais, ao mesmo tempo em que utiliza linguagens de programação probabilísticas.
 usando Previsão usando a órbita
usando Previsão usando a órbita
Para saber mais sobre a Orbit, acesse este link.
PyCaret
PyCaret é uma biblioteca de aprendizado de máquina de código aberto e de baixo código em Python que automatiza os fluxos de trabalho de aprendizado de máquina. Com o PyCaret, você passa menos tempo codificando e mais tempo analisando. Você pode treinar seu modelo, analisá-lo, iterar com mais rapidez do que nunca e implantá-lo instantaneamente como uma API REST ou até mesmo criar um aplicativo de ML de front-end simples, tudo a partir do seu Notebook favorito.
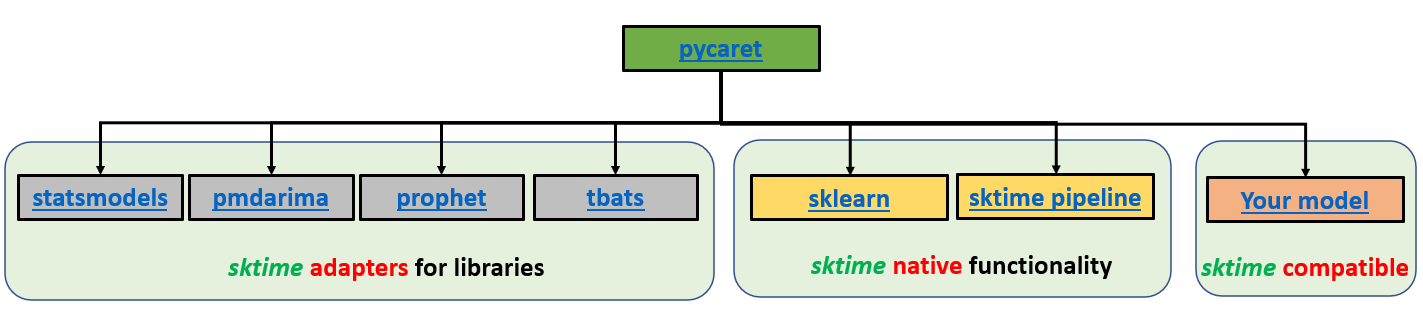 Arquitetura do módulo de séries temporais PyCaret. Desenvolvido pelo desenvolvedor líder Nikhil Gupta.
Arquitetura do módulo de séries temporais PyCaret. Desenvolvido pelo desenvolvedor líder Nikhil Gupta.
A seguir, veremos um exemplo de uma tarefa de previsão de série temporal de ponta a ponta usando a biblioteca PyCaret.
Exemplo de ponta a ponta
O módulo de série temporal do PyCaret está disponível em versão beta, você pode baixá-lo do pip.
pip install pycaret-ts-alpha
Link para este tutorial no Colab.
Conjunto de dados
Aqui, usamos o conjunto de dados da companhia aérea, que também está disponível no repositório de dados do PyCaret.
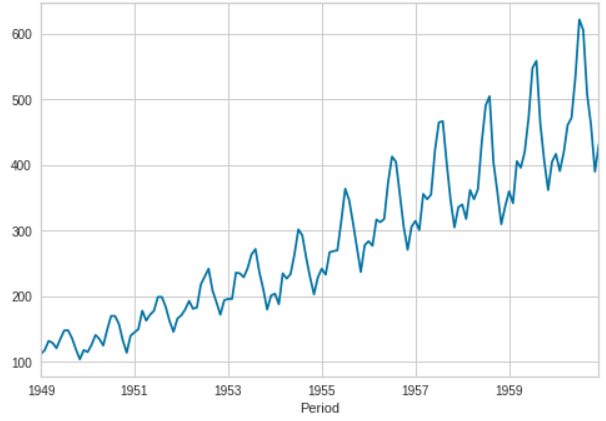
from pycaret.datasets import get_data
data = get_data('airlineer')

data.plot()
Experimento de configuração
Os experimentos no PyCaret são iniciados usando a função setup. Essa função cuida de todas as etapas de pré-processamento, divisão de treinamento-teste, estratégia de validação cruzada e algumas outras tarefas.
from pycaret.time_series import *
s = setup(data, session_id = 123)
 Saída da função de configuração
Saída da função de configuração
Análise exploratória de dados (EDA)
Quando se trata de EDA de dados de séries temporais univariadas, há algumas coisas que você pode e deve fazer.
Para o uso de modelos clássicos e estatísticos, você pode executar alguns testes estatísticos. Há uma função no PyCaret que faz isso para você.
check_stats()
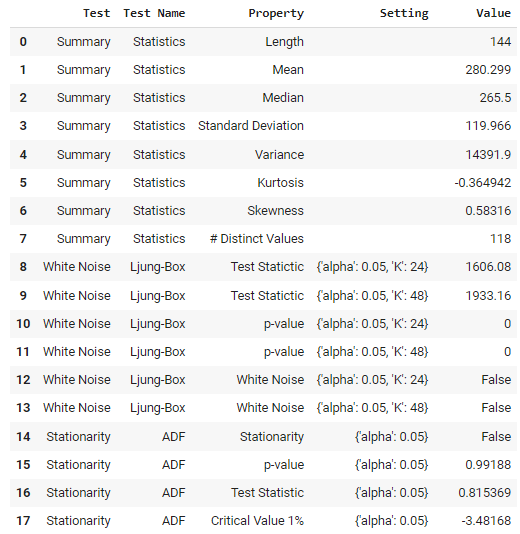 Saída da função check_stats
Saída da função check_stats
Se estiver lidando com séries temporais univariadas, você também poderá decompô-las em componentes de tendência, sazonalidade e erro para qualquer análise posterior.
plot_model(plot = 'decomp_classical")
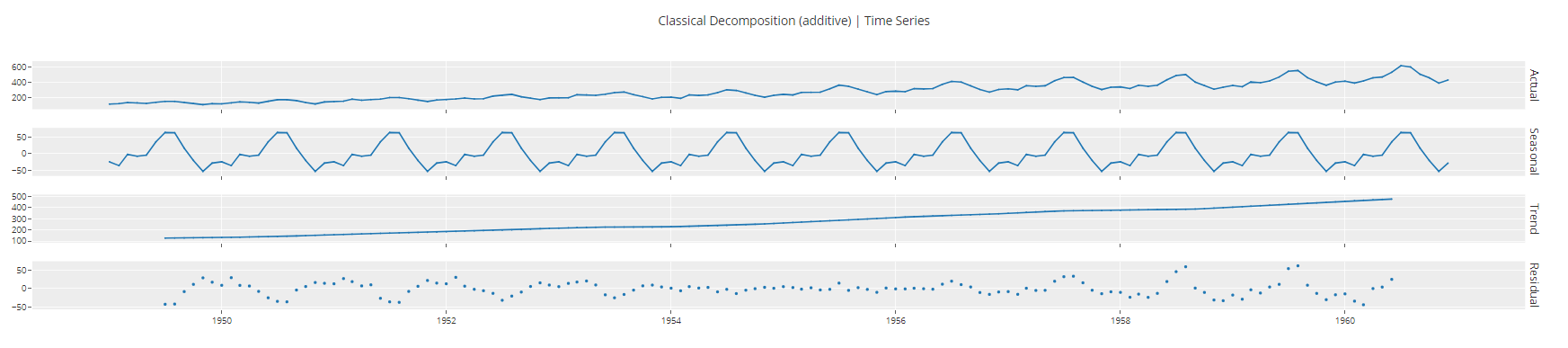 Saída da função plot_model<c/entre> ## Treinamento e seleção de modelos ## Para treinar vários modelos e selecionar um entre muitos, executamos apenas uma linha de código.
Saída da função plot_model<c/entre> ## Treinamento e seleção de modelos ## Para treinar vários modelos e selecionar um entre muitos, executamos apenas uma linha de código. best = compare_models() 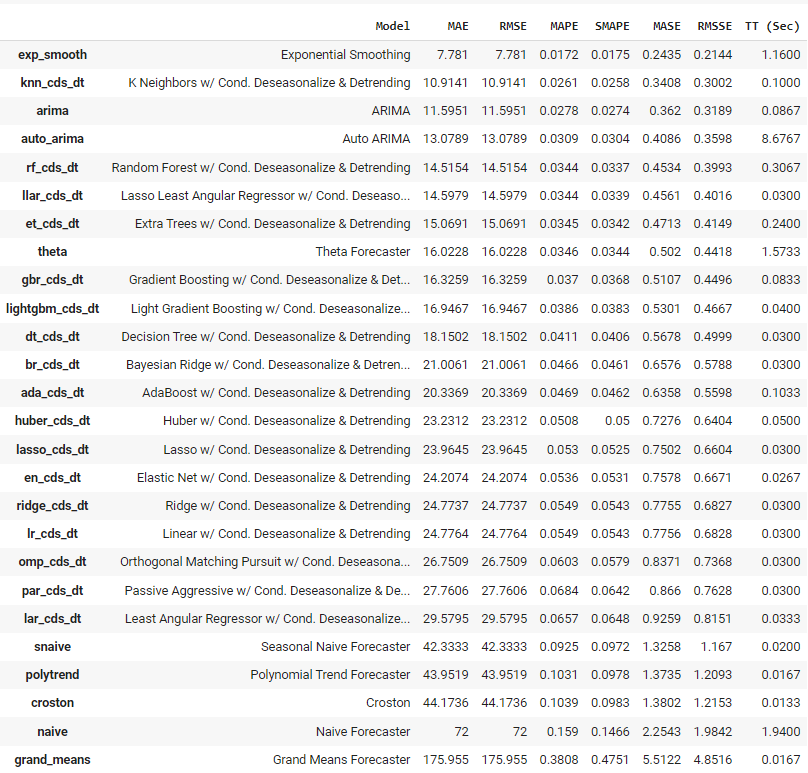 Saída da função compare_models
Saída da função compare_models
O PyCaret treinou mais de 25 modelos usando a validação cruzada apropriada para séries temporais e apresentou uma lista de modelos em ordem de maior para menor desempenho. O melhor modelo baseado nesse experimento para esse conjunto de dados é o Exponential Smoothing, com um erro absoluto médio de 7,781.
Análise de modelos
Antes de implementarmos esse modelo para gerar previsões para o futuro, podemos ver alguns gráficos de análise para comentar sobre a qualidade do nosso modelo.
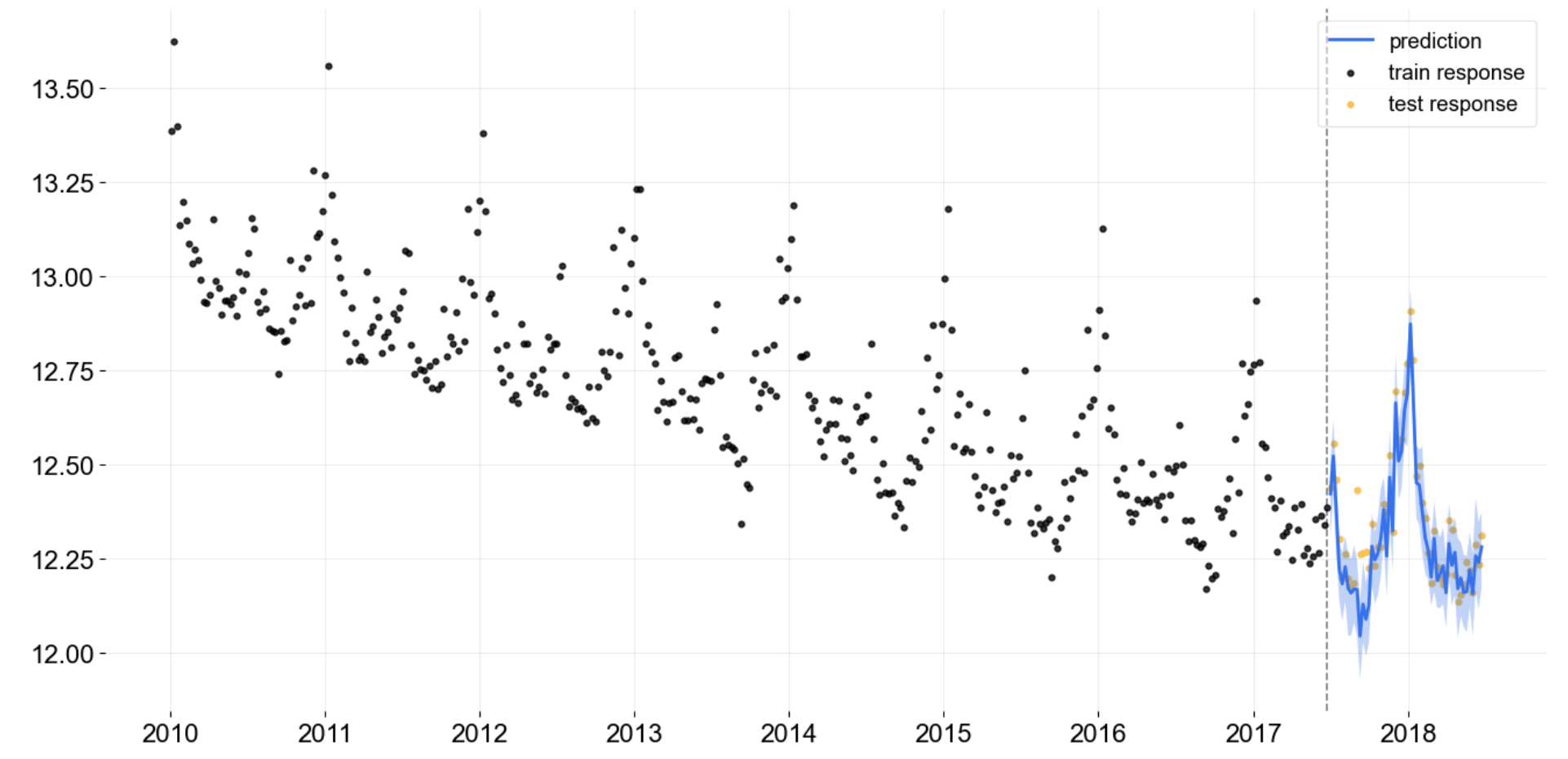
plot_model(best, plot = 'forecast', data_kwargs = {'fh': 24})
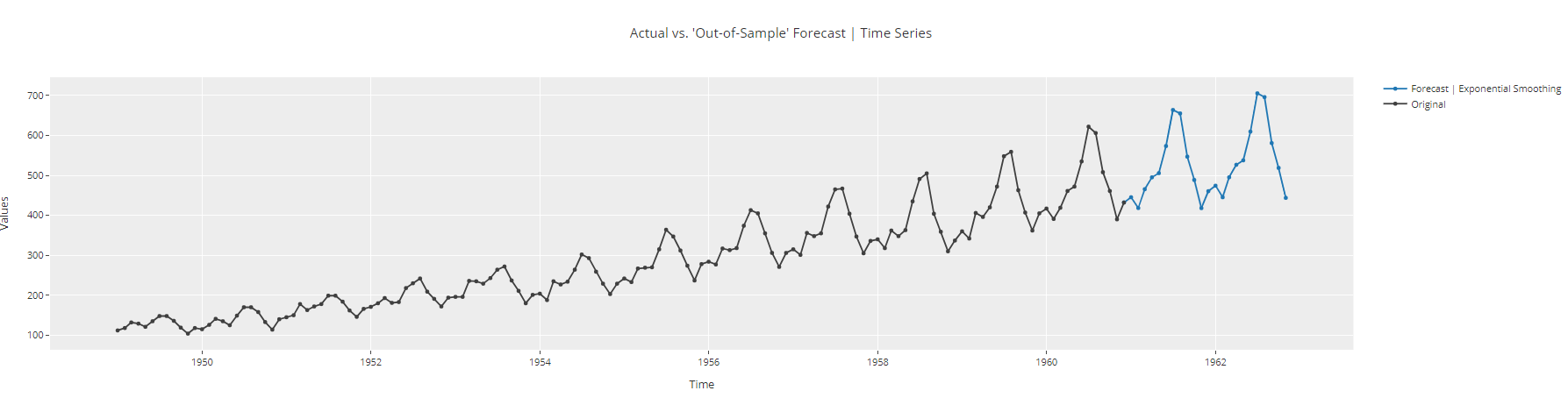 de Gráfico de previsão de série temporal
de Gráfico de previsão de série temporal
plot_model(best, plot = 'residuals')
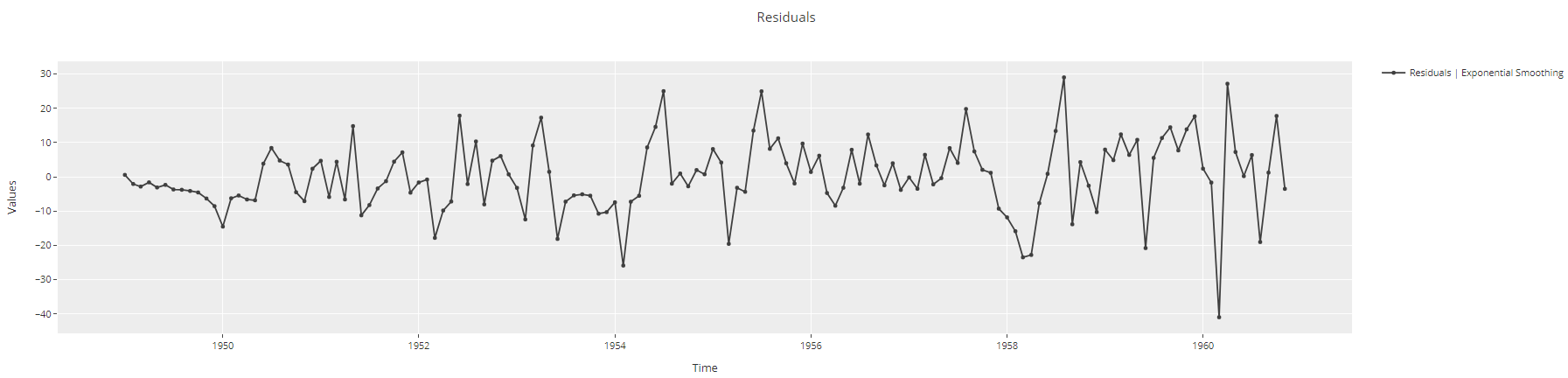 de resíduos de Gráfico de resíduos de séries temporais
de resíduos de Gráfico de resíduos de séries temporais
plot_model(best, plot = 'insample')
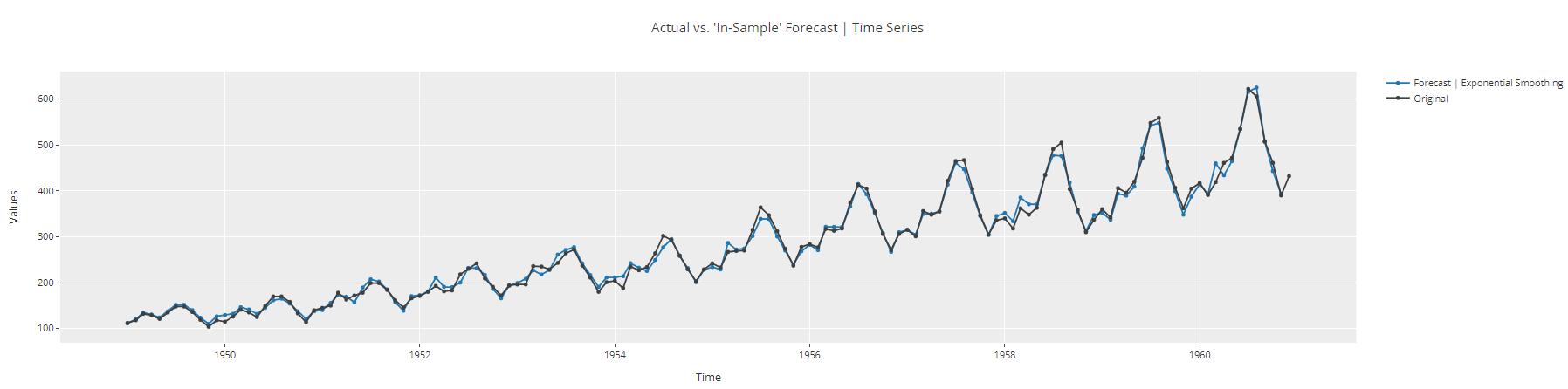 de sem Gráfico de série temporal sem amostra
de sem Gráfico de série temporal sem amostra
Implementação do modelo
Neste ponto, estamos prontos para finalizar o modelo e salvá-lo para uso futuro.
# finalize model
final_best = finalize_model(best)
# save model
final_best = finalize_model(best)

Para carregar esse arquivo novamente e gerar previsões sobre dados futuros:
# load model
loaded_model = load_model('my_best_model')
# generate predictions for the next 48 months
predict_model(loaded_model, fh = 48)
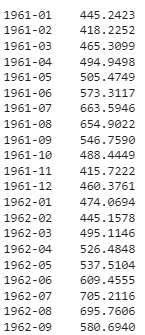 Saída truncada
Saída truncada
Saiba mais sobre o PyCaret
| ⭐ Tutoriais | Confira os tutoriais oficiais. |
|---|---|
| Notebooks | Exemplos de cadernos criados pela comunidade. |
| 📙 Blog | Tutoriais e artigos de colaboradores. |
| 📚 Documentação | A documentação detalhada da API do PyCaret |
| 📺 Tutoriais em vídeo | Tutorial em vídeo do PyCaret de vários eventos. |
Conclusão
A previsão de séries temporais é uma habilidade muito útil para você aprender. Muitos problemas da vida real são de natureza de série temporal. A previsão tem uma série de aplicações em vários setores, com inúmeras aplicações práticas, incluindo: previsão do tempo, previsão econômica, previsão de saúde, previsão financeira, previsão de varejo, previsão de negócios, estudos ambientais, estudos sociais e muito mais.
Basicamente, qualquer dado histórico com intervalos consistentes pode ser analisado com métodos de análise de séries temporais que levam a uma tarefa de previsão que aprende com os dados históricos e tenta prever o futuro. Para concluir, há três categorias amplas para a previsão de séries temporais:
- Modelos estatísticos - suavização exponencial, ARIMA, SARIMA, TBATS, etc.
- Aprendizado de máquina - Regressão linear, XGBoost, Random Forest, etc.
- Aprendizagem profunda - RNN, LSTM
Se você quiser aprofundar seus conhecimentos e habilidades em previsão de séries temporais, confira este incrível curso "Time Series with Python" da Datacamp. Neste curso, você aprenderá a manipular dados de séries temporais usando pandas, trabalhará com bibliotecas estatísticas, incluindo NumPy e statsmodels, para analisar dados e desenvolverá suas habilidades de visualização usando Matplotlib, SciPy e seaborn. Ao final deste curso, você saberá como prever o futuro usando modelos de classe ARIMA e gerar previsões e insights usando modelos de aprendizado de máquina.