Media Winsorizada: Un enfoque robusto para tratar los valores atípicos

Los valores atípicos a menudo pueden desviar tus percepciones, convirtiendo lo que debería ser un análisis significativo en una conclusión engañosa. Los datos imperfectos y ruidosos son habituales en el mundo real, y la winsorización es una solución práctica para reducir el impacto de los valores atípicos sin descartar ningún dato.

Este artículo explorará cómo funciona la media winsorizada, sus aplicaciones prácticas y los pasos para calcularla utilizando Python. También conoceremos sus pros y sus contras, la compararemos con otras medidas útiles, como la media recortada, y exploraremos otras medidas estadísticas de winsorización.

¿Qué es una media winsorizada?

Una media winsorizada es una medida estadística que reduce el impacto de los valores atípicos sustituyendo los valores extremos por percentiles menos extremos, en lugar de eliminarlos por completo. A diferencia de la media aritmética, que considera todos los puntos de datos por igual, la media winsorizada limita la influencia de los valores extremos que pueden distorsionar el resultado global.

La winsorización funciona limitando o sustituyendo los valores que superan un determinado umbral percentil. Por ejemplo, en una winsorización del 5%, el 5% más bajo de los puntos de datos se sustituye por el valor del percentil 5, y el 5% más alto se sustituye por el valor del percentil 95. Este método ayuda a conservar la estructura general del conjunto de datos al tiempo que reduce el efecto de los valores atípicos, lo que lo convierte en una alternativa sólida a la media estándar en conjuntos de datos que contienen valores extremos.

Aplicaciones prácticas de la media winsorizada

La relevancia de la media winsorizada en el análisis estadístico es especialmente evidente en campos en los que los datos son propensos a distribuciones sesgadas. He aquí algunas áreas clave en las que la media winsorizada resulta útil:

• Finanzas y Análisis de Inversiones: Los conjuntos de datos financieros suelen contener valores extremos, como caídas del mercado o ganancias excepcionales, que pueden distorsionar las medias y oscurecer las tendencias. Los analistas pueden producir métricas de rendimiento más estables que reflejen mejor el comportamiento típico del mercado winsorizando los rendimientos o los precios de los activos.
• Datos económicos: En los estudios macroeconómicos, indicadores como la distribución de la renta o la riqueza suelen estar sesgados por un pequeño número de valores extremadamente altos o bajos. Las medias winsorizadas pueden ofrecer una visión más equilibrada de las condiciones económicas, al limitar la influencia de estas observaciones extremas.
• Encuesta e Investigación en Ciencias Sociales: Las encuestas pueden arrojar datos con respuestas extremas, como valoraciones demasiado altas o bajas. En estos casos, la media winsorizada proporciona una medida más precisa de la tendencia central, garantizando que las respuestas extremas no afecten desproporcionadamente al análisis global.
• Investigación Médica y Biológica: Los datos médicos, como los resultados de los pacientes o de las pruebas, a veces pueden mostrar valores extremos debido a condiciones poco frecuentes o casos atípicos. Winsorizar estos datos puede ayudar a los investigadores a obtener una imagen más precisa de los resultados medios sin eliminar por completo puntos de datos potencialmente valiosos.

En cada una de estas aplicaciones, la media winsorizada es una alternativa robusta a la media estándar, que permite a los analistas obtener perspectivas menos afectadas por los valores atípicos, preservando al mismo tiempo importantes patrones de datos.

Cómo calcular la media winsorizada en Python

Calcular la media winsorizada en Python implica sustituir los valores extremos (outliers) por valores en percentiles específicos. Antes de empezar, un rápido resumen de los pasos que vamos a seguir:

• Importa las bibliotecas y el conjunto de datos necesarios.

• Winsoriza el conjunto de datos utilizando scipy.winsorize().

• Calcula la media utilizando numpy.mean().

Profundicemos en los detalles con un ejemplo. 

Importa las bibliotecas y el conjunto de datos necesarios

En primer lugar, importaremos las bibliotecas necesarias para calcular la media.

import numpy as np
from scipy.stats.mstats import winsorize

A continuación, cargamos el conjunto de datos, que puede proceder de un archivo CSV o de cualquier otra fuente de datos. Para simplificar el ejemplo, crearemos un conjunto de datos de muestra utilizando numpy.

data = np.array([10, 12, 14, 15, 16, 18, 20, 22, 24, 25, 30, 35, 40, 45, 50, 60, 70, 80, 82, 85, 90, 200])

Según un análisis inicial, 200 podría considerarse un valor atípico en este conjunto de datos.

Winsorizar el conjunto de datos 

La función winsorize() de la biblioteca scipy te permite especificar el porcentaje de datos a winsorizar de las colas inferior y superior. El código para hacerlo es el siguiente

# Winsorize 5% from both the lower and upper tails
winsorized_data = winsorize(data, limits=[0.05, 0.05])

En el código anterior, el parámetro limits=[0.05, 0.05] introducido en la función winsorize() sustituye el 5% más pequeño y el 5% más grande de los valores por los valores de los percentiles 5 y 95, respectivamente. Ahora podemos inspeccionar los datos winsorizados que hemos creado.

print("Original data: ", data)
print("Winsorized data: ", winsorized_data)

La salida mostrará que se han sustituido los valores atípicos:

Original data: [ 10 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 200]
Winsorized data: [ 12 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 90]

Aquí, el valor máximo 200 se ha sustituido por 90; del mismo modo, los valores extremos del extremo inferior, 10, se han sustituido por 12.

Calcula la media 

Por último, calculemos la media de los datos winsorizados:

winsorized_mean = np.mean(winsorized_data)
print("Winsorized mean: ", winsorized_mean)

El resultado es el siguiente:

Winsorized mean: 42.5

La media winsorizada ha reducido la influencia de los valores extremadamente altos en comparación con una media regular. Para comparar, podemos calcular la media original del siguiente modo:

original_mean = np.mean(data)
print("Original mean: ", original_mean)

El resultado es el siguiente:

Original mean: 47.40909090909091

Los valores atípicos influyen mucho en la media original en 47.40, haciendo que sea significativamente más alta. Tras winsorizar los valores extremos, la media winsorizada es mucho más baja en 42.5, con menor influencia de los valores extremos.

Media winsorizada vs. Media recortada: Diferencias clave

Tanto la media winsorizada como la media recortada son métodos estadísticos utilizados para reducir el efecto de los valores atípicos en la media, pero difieren en cómo tratan los valores extremos:

• La media winsorizada sustituye los valores extremos (valores atípicos) en ambos extremos de los datos por los valores más cercanos dentro del conjunto de datos. No descarta los datos, sino que ajusta los valores más extremos para reducir su impacto.
• La media recortada elimina (recorta) el porcentaje más bajo y más alto de puntos de datos. Este método descarta una parte de los datos en ambos extremos. En una media recortada al 5%, el 5% más pequeño y el 5% más grande de los puntos de datos se excluyen del cálculo de la media.

La media winsorizada es preferible cuando quieres conservar la estructura de los datos (es decir, mantener el mismo tamaño de la muestra) pero reducir el efecto de los valores extremos. La media recortada es preferible cuando el conjunto de datos contiene valores atípicos claros que quieres eliminar por completo y cuando es aceptable un tamaño de muestra menor tras el recorte.

Comparar la media recortada y la media winsorizada en Python

Veamos cómo afectan ambos métodos al conjunto de datos y comparemos sus resultados.

from scipy.stats import trim_mean

# Calculate the Trimmed mean by removing 5% from both tails
trimmed_mean = trim_mean(data, proportiontocut=0.05)

# Print the results
print("Original mean: ", np.mean(data))
print("Winsorized mean (5%): ", winsorized_mean)
print("Trimmed mean (5%): ", trimmed_mean)

El resultado es el siguiente:

Original mean: 47.40909090909091
Winsorized mean (5%): 42.5
Trimmed mean (5%): 41.65

La media original era 47.4, muy influida por los valores atípicos. La media winsorizada, 42.5, se calculó sustituyendo los valores atípicos por valores menos extremos. La media recortada, cuando se han eliminado completamente los valores atípicos, es 41.65.

Saber cuándo utilizar cada método

Utiliza la media winsorizada cuando quieras conservar todos los puntos de datos pero reducir el impacto de los valores extremos. Es una buena heurística, porque la media winsorizada es útil cuando crees que los valores atípicos son auténticos, pero quieres minimizar su influencia.

Utiliza la media recortada cuando quieras eliminar por completo los valores atípicos del conjunto de datos. La media recortada es más útil cuando sospechas que los valores atípicos son erróneos o no son representativos de la distribución de los datos.

Resumen de las principales diferencias

Las diferencias resumidas pueden tabularse como sigue:

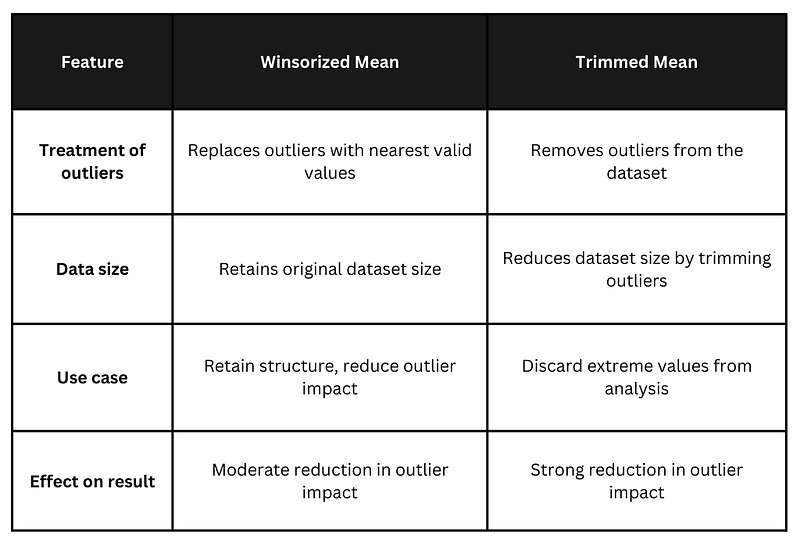Diferencias clave entre media winsorizada media recortadaDiferencias clave entre la media winsorizada y la media recortada. Imagen del autor.

Las medias winsorizadas y recortadas ayudan a manejar los valores atípicos, pero la elección depende de si quieres conservar o descartar los valores extremos del conjunto de datos.

Ventajas e inconvenientes de la media winsorizada

Aunque el proceso de winsorización es un método sólido para tratar los valores atípicos, modificar los valores extremos podría suscitar dudas sobre la manipulación de los datos. He aquí algunas ventajas e inconvenientes de la técnica:

Ventajas

• Más robusta que la media estándar en presencia de valores atípicos: La media winsorizada reduce el impacto de los valores extremos (valores atípicos), ofreciendo una tendencia central más estable y fiable en conjuntos de datos en los que los valores atípicos pueden distorsionar el resultado.
• Mantiene la estructura general del conjunto de datos conservando todos los puntos de datos: A diferencia de la media recortada, que descarta los valores extremos, la media winsorizada los sustituye por valores menos extremos, manteniendo el tamaño de la muestra y la estructura general del conjunto de datos.
• Más adecuado para conjuntos de datos pequeños: En los conjuntos de datos en los que la eliminación de puntos de datos (como en el recorte) daría lugar a una muestra no representativa o incompleta, la winsorización conserva todos los valores, garantizando que el conjunto de datos siga siendo utilizable.

Inconvenientes

• Puede introducir un sesgo si la distribución de los datos subyacentes es asimétrica: La winsorización de datos basada en percentiles fijos (por ejemplo, 5% de ambos extremos) puede introducir sesgos si el conjunto de datos no está distribuido simétricamente. Si los datos están sesgados, la winsorización podría distorsionar la tendencia central en lugar de reflejarla con precisión.
• Requiere una selección cuidadosa del porcentaje de winsorización: El porcentaje de datos a winsorizar (es decir, la proporción de valores extremos a modificar) suele elegirse arbitrariamente. Seleccionar un porcentaje inadecuado puede no mitigar suficientemente el impacto de los valores atípicos o alterar demasiados valores, reduciendo la representatividad del conjunto de datos.
• Una excesiva glorificación de los datos puede ocultar patrones significativos: Una excesiva winsorización, o la modificación de demasiados puntos de datos, puede oscurecer patrones o tendencias significativos en los datos. En algunos casos, los valores extremos representan información válida y vital (por ejemplo, en los datos financieros, donde los valores atípicos podrían significar acontecimientos raros pero impactantes), y sustituirlos podría llevar a conclusiones engañosas.

Por ello, es importante considerar los pros y los contras de utilizar la técnica antes de incorporarla a nuestros proyectos de análisis de datos.

Otros conceptos estadísticos winsorizados

Dado que la winsorización es una técnica estadística aplicada a una medida, puede extenderse a otras medidas estadísticas habituales. Exploremos otras medidas a las que se puede aplicar la winsorización:

• Desviación winsorizada de la muestra: La versión winsorizada de la desviación típica mide la dispersión de un conjunto de datos winsorizados sustituyendo los valores extremos. Calculada como la raíz cuadrada de la varianza Winsorizada.
• Varianza winsorizada: La contrapartida winsorizada de la varianza mide cuánto se desvían los puntos de datos de la media winsorizada, teniendo en cuenta la influencia reducida de los valores atípicos. Se calcula como la media de las desviaciones al cuadrado de la media winsorizada en un conjunto de datos winsorizados.
• Rango winsorizado: La diferencia entre los valores máximo y mínimo del conjunto de datos winsorizado, que es menor que el rango original debido a la sustitución de los valores atípicos.
• Asimetría winsorizada: Mide la asimetría de la distribución de un conjunto de datos winsorizado, indicando si la distribución está sesgada a la izquierda o a la derecha tras la winsorización. Ayuda a identificar la asimetría en conjuntos de datos en los que los valores extremos pueden distorsionar el cálculo estándar de la asimetría.
• Correlación winsorizada: Una versión winsorizada de la correlación de Pearson evalúa la relación lineal entre dos variables al tiempo que reduce el impacto de los valores atípicos en ambos conjuntos de datos.

Cada una de estas medidas winsorizadas ayuda a reducir la influencia de los valores atípicos en el análisis cuando se trabaja con datos no normales o conjuntos de datos con valores extremos.

Conclusión

Este tutorial introdujo una medida estadística para tratar los valores atípicos: la media winsorizada. Aprendimos el concepto de winsorización, sus aplicaciones prácticas y una implementación práctica en un conjunto de datos de muestra. Además, el tutorial trata sobre la media recortada, su aplicación y en qué se diferencia de la media winsorizada. También exploró los pros, los contras y otros conceptos estadísticos basados en la winsorización. 

Como hemos visto, la media winsorizada equilibra descartar los valores atípicos y mantenerlos, lo que permite obtener resultados más fiables en conjuntos de datos sesgados. Te animamos a que utilices la técnica en tus proyectos de análisis de datos, experimentando con distintos niveles de winsorización para encontrar lo que mejor funciona para conjuntos de datos concretos.

Consulta nuestro curso de Análisis Predictivo Intermedio en Python para aprender más sobre el manejo de valores atípicos en conjuntos de datos utilizando Python, incluida la winsorización. También puedes explorar nuestro itinerario profesional de Científico de Aprendizaje Automático con Python, que es una forma estupenda de practicar construyendo algunos modelos reales.