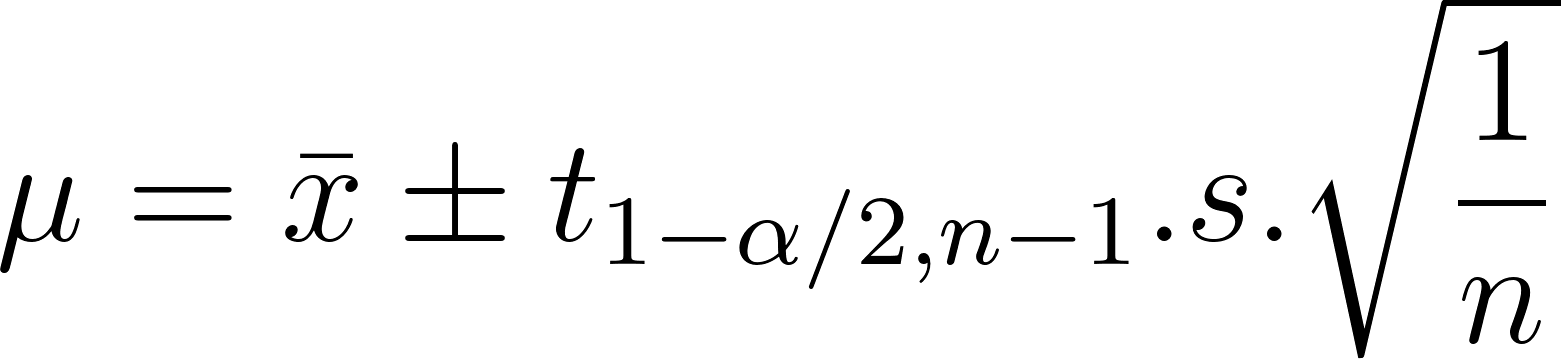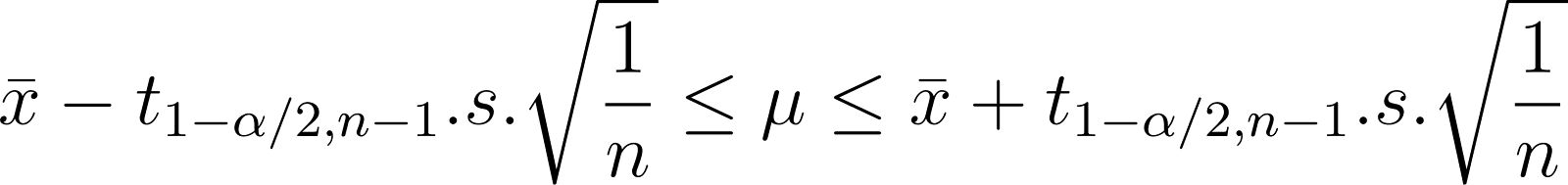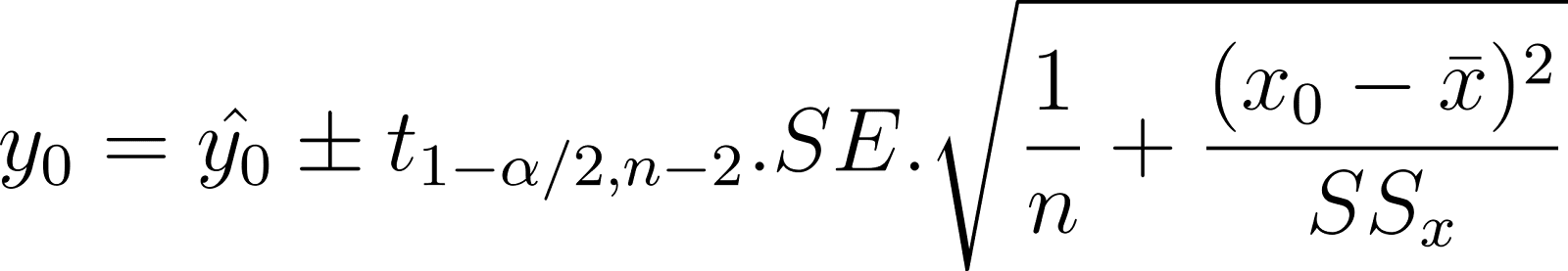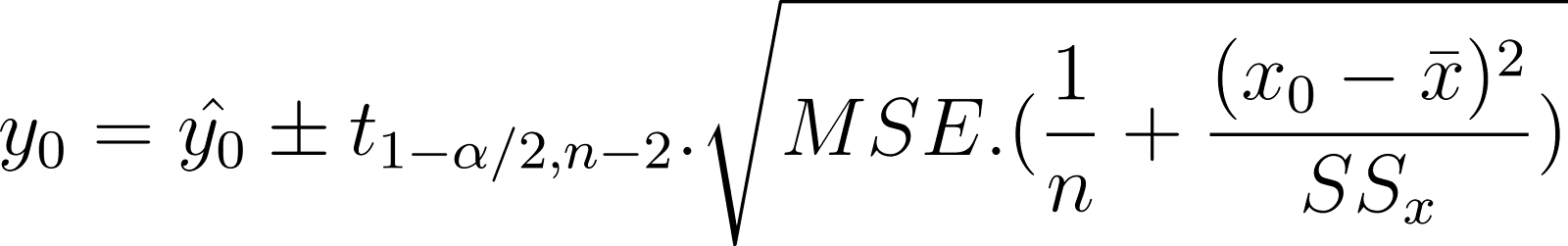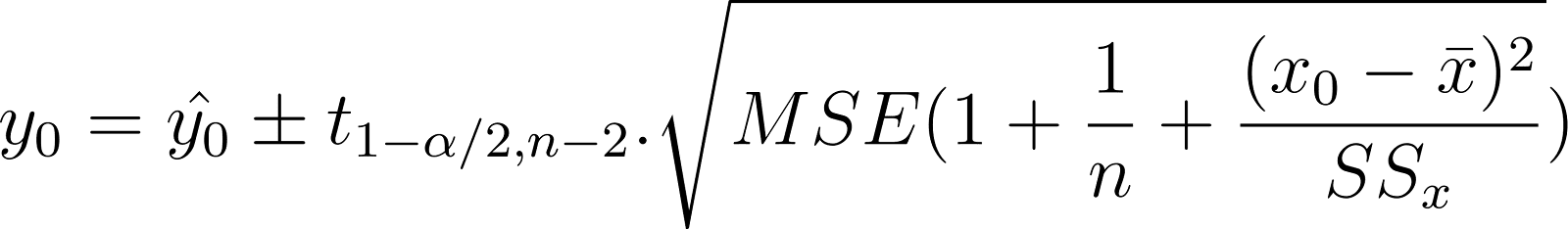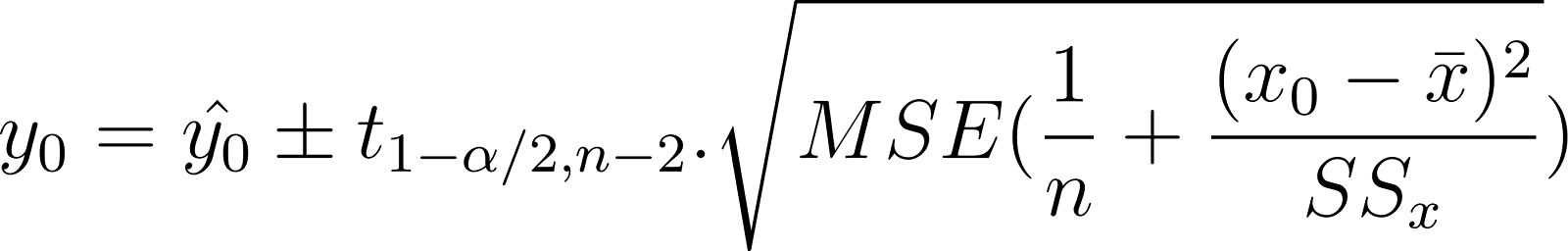Intervalos de confianza frente a intervalos de predicción: Comprender la diferencia

Diferencias entre intervalos de predicción e intervalos de confianza

Los dos conceptos -intervalos de predicción e intervalos de confianza- están estrechamente relacionados. Un mismo análisis puede implicar a menudo el uso de ambos tipos de intervalos. Por tanto, es útil compararlos cara a cara. 

Finalidad e interpretación

Cuando necesitas conocer un parámetro poblacional, como la media, utilizas una muestra para estimar dicho parámetro. Como el tamaño de la muestra suele ser mucho menor que el de la población, la estimación del parámetro de la muestra es imperfecta. El intervalo de confianza es el rango (de la estimación muestral) que se espera que contenga el parámetro poblacional. 

Los coeficientes de regresión también se consideran parámetros poblacionales. Como se estiman a partir de una muestra (y no de toda la población), estos parámetros contienen cierto error. Así, los coeficientes de regresión también pueden expresarse con un intervalo de confianza. 

Además, puedes utilizar la regresión para predecir cualquiera de las dos cosas:

• El valor medio de una variable dependiente (como el peso medio de los perros de 2 años) o
• El valor de un punto de datos individual (como un perro individual de 2 años). 

El primero utiliza un intervalo de confianza, y el segundo, un intervalo de predicción. En el apartado siguiente se explica esta diferencia con más detalle.

Cálculo y amplitud del intervalo

Cálculo del intervalo de confianza para la inferencia estadística 

Como ya se ha explicado, el intervalo de confianza es proporcional a la desviación típica e inversamente proporcional al tamaño de la muestra. El intervalo de confianza de la media de la población, 𝛍, se expresa como:

En la expresión anterior:

• x es la media muestral, la estimación, que puedes medir
• 𝛍 es la media poblacional, el parámetro poblacional que quieres estimar. 
• n es el tamaño de la muestra
• s es la desviación típica de la muestra
• t es el valor crítico de la distribución T de Student en
• Nivel de significación de 1 - α
• n-1 grados de libertad
• Puedes encontrar los valores T de las tablas estandarizadas: busca en Google "Tabla T de Student". 

Por tanto, el rango de 𝛍 es:

Comprender los niveles de confianza y los niveles de significación 

Observa también que el tamaño del intervalo es proporcional al valor t. Si quieres un grado de confianza (certeza) extremadamente alto de que el valor real se encuentra dentro del intervalo dado, ese intervalo tiene que ser muy grande. Cuanto menor sea el grado de confianza, más estrecho será el intervalo. Pero un grado de confianza muy bajo no es muy útil. Así que, en la práctica, es habitual elegir niveles de confianza del 90%, 95%, 99%, etc. 

Si tienes un nivel de confianza del 95%, te lleva a un nivel de significación del 5%. Suponiendo un intervalo de dos caras, tienes que encontrar el valor crítico t al 2,5% (0,025). 

Conceptualmente, todos los intervalos se expresan del siguiente modo:

Observa que, en todos los casos, cuanto mayor es el error, más amplio es el intervalo. Este error se calcula de forma diferente según el caso de uso. Para la inferencia, el error es la desviación típica. Para la regresión, el error se muestra en las secciones siguientes. 

Cálculo del intervalo de confianza para la regresión 

Cuando predices el valor medio de la variable dependiente, estimas su rango utilizando el intervalo de confianza. Por ejemplo, quieres predecir un intervalo para el peso medio de los perros de 2 años en función de su edad. Esto se llama intervalo de confianza de la respuesta media. También se considera un parámetro poblacional porque es una propiedad de toda la población. El intervalo se expresa como

En la expresión anterior:

• y0 es el valor verdadero del parámetro predicho.
• y0 es el valor predicho utilizando la relación de regresión.
• El valor t crítico se explica en la sección anterior
• n es el tamaño de la muestra
• (x0 -x) es la diferencia entre el valor medio de x y x0para el que intentas predecir y0. Observa que cuanto mayor sea esta diferencia, mayor será el intervalo. Así, se obtienen intervalos estrechos (y predicciones más precisas) para valores de xpróximos a la media de la muestra .
• SSx es la desviación al cuadrado de la muestra de valores x. Se expresa como:

• SE es el error típico de la estimación. Es la raíz cuadrada del error cuadrático medio (ECM). El MSE es la varianza del error. Así pues, el SE es análogo a la desviación típica del error. El MSE se basa en el error residual. Se expresa como: 

En la expresión anterior, el término sumatorio también se denomina suma de cuadrados de los residuos. El residuo es la diferencia entre el valor real de y y el valor predicho de y. 

Utilizando el MSE en lugar del SE, el intervalo de confianza de la respuesta media también puede escribirse como:

Compara la expresión anterior con la relación conceptual mostrada anteriormente. 

Observa que el error tiene en cuenta

• La diferencia entre los valores reales y previstos de y.
• La diferencia entre el valor medio de x y el valor de xopara el que quieres generar la predicción
• La dispersión global de x (respecto a su media)

Cálculo del intervalo de predicción para la regresión 

Para predecir el valor exacto de un punto de datos individual (no la media), estima su rango utilizando el intervalo de predicción. Por ejemplo, quieres predecir el intervalo del peso real de un perro concreto de 2 años en función de su edad. Esto se denomina intervalo de predicción, y se expresa como:

Compáralo con el intervalo de confianza mostrado anteriormente:

Observa que ambas expresiones son bastante similares. La única diferencia es el término de error adicional en el intervalo de predicción. El intervalo de predicción tiene un término MSE adicional dentro de la raíz cuadrada que el intervalo de confianza. Esto es para tener en cuenta la variabilidad de los valores y, que quieres predecir. Esto hace que el intervalo de predicción sea más amplio que el intervalo de confianza. 

El esquema siguiente muestra los intervalos de confianza y predicción en relación con la estimación puntual (valor predicho).

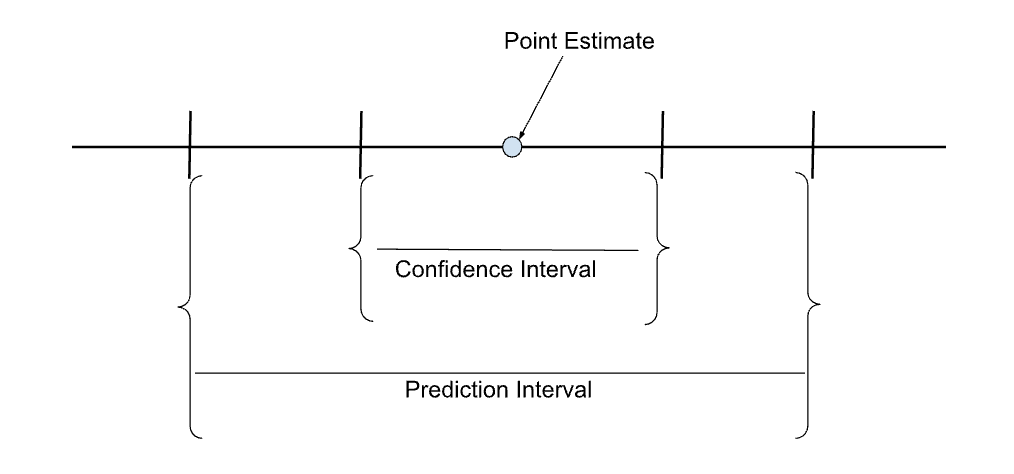
Comparar los intervalos de confianza y predicción de una estimación puntual. Imagen del autor.

El esquema siguiente muestra los intervalos de confianza y de predicción en relación con la regresión; observa también que los intervalos son más estrechos en la región de la media. 

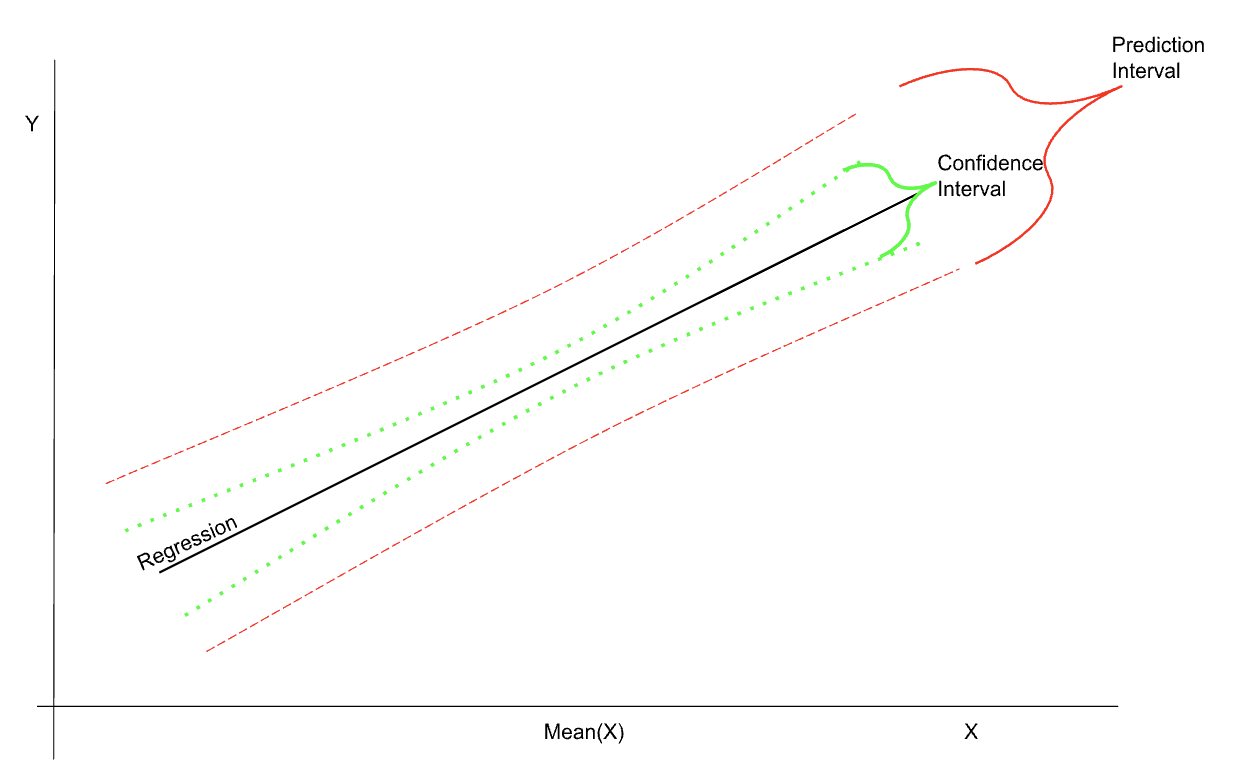
Ilustración de los intervalos de confianza y predicción en regresión. Imagen del autor.

Cuándo utilizar un intervalo de confianza

En los apartados anteriores se han tratado los fundamentos de los intervalos de confianza y de predicción, sus usos y las fórmulas utilizadas para calcularlos. En este apartado se dan ejemplos prácticos de cuándo utilizar intervalos de confianza y de predicción. 

Un intervalo de confianza se utiliza cuando se estima un parámetro poblacional. Para estimar el parámetro poblacional, puedes

1. Utiliza mediciones directas basadas en una muestra aleatoria
2. Utilizar un modelo de regresión basado en una muestra aleatoria

Algunos ejemplos de uso del intervalo de confianza son:

• Estimación de un parámetro poblacional a partir de la medición de una muestra aleatoria. Por ejemplo, para calcular la altura y el peso medios de los recién nacidos, tomas las medidas de una muestra aleatoria de recién nacidos. 
• Estimar el comportamiento de una población estudiando una muestra aleatoria. Este caso de uso es habitual en los ensayos clínicos, en los que se intenta estimar los efectos de un fármaco en la población estudiando sus efectos en una muestra aleatoria. 
• Predecir la respuesta media de una variable dependiente a partir de un análisis de regresión realizado sobre una muestra aleatoria. Por ejemplo, quieres predecir el peso medio de cachorros de 55 días basándote en una muestra de pesos de cachorros medidos cada 15 días. 
• Fijación de los límites de tolerancia en los procesos de fabricación. Por ejemplo, si una máquina produce piezas de un peso especificado, no todas las piezas tienen exactamente el mismo peso que la especificación. El peso de cada pieza se encuentra dentro de un intervalo de confianza del peso especificado. Este intervalo es el límite de tolerancia. Se rechazan las piezas con pesos superiores a los límites de tolerancia. Se espera que la máquina produzca piezas que, en su mayoría, estén dentro del límite de tolerancia. 
• Control de calidad. Supón que quieres establecer si las piezas producidas por una máquina están dentro del límite de tolerancia. No es posible medir todas las piezas. Tienes que basarte en tomar muestras aleatorias, medirlas y luego utilizar las estimaciones de la muestra para calibrar los parámetros de la población. 
• Comprobación de hipótesis. Los niveles de confianza y los niveles de significación son dos caras de la misma moneda. Nivel de significación = 1 - Nivel de confianza.  Un intervalo de confianza, con un nivel de confianza especificado, incluye los puntos de datos para los que la hipótesis nula es cierta con un nivel de significación de (1 - el nivel de confianza especificado). 

Cuándo utilizar un intervalo de predicción

Los intervalos de predicción se utilizan siempre que predices el valor esperado de un punto de datos individual basándote en observaciones de (y análisis de regresión sobre) una muestra aleatoria. 

Algunos ejemplos prácticos son: 

• Predecir el rango de un punto de datos individual basándose en un análisis de regresión. Como los puntos de datos individuales pueden tener mayor variabilidad (que la media muestral), necesitas un intervalo de predicción más amplio. Por ejemplo, quieres predecir el peso de un cachorro individual de 55 días basándote en una muestra aleatoria de pesos de cachorros medidos cada 15 días. 
• Puedes utilizar simulaciones de Montecarlo para predecir el valor de una variable desconocida. Como los métodos de Montecarlo son probabilísticos, obtendrás un resultado ligeramente distinto cada vez que ejecutes el modelo. Estas diferencias entre las distintas salidas se codifican en el Intervalo de Incertidumbre de Montecarlo, que es conceptualmente similar a un intervalo de predicción. 
• En la regresión estándar, construyes una relación para predecir el valor medio de un parámetro. En la regresión cuantil, construyes modelos diferentes para predecir cada cuantil del parámetro objetivo. Esto también te permite construir intervalos de predicción más granulares. 
• Los modelos de aprendizaje automático se ocupan de predecir el valor de un parámetro desconocido. Estos modelos suelen basarse en métodos estadísticos y, por tanto, predicen el valor medio de la cantidad desconocida. Así, el resultado del modelo incluye tanto el valor esperado (medio) como el intervalo de predicción. 
• Los modelos de aprendizaje profundo utilizan una serie de redes neuronales para hacer predicciones. Para evaluar la incertidumbre en la salida, es habitual dejar caer aleatoriamente diferentes neuronas para estudiar la variabilidad en la salida. La varianza de estas predicciones se utiliza para construir el intervalo de predicción. 
• En la previsión de series temporales, el objetivo es predecir el valor de un observable en un paso temporal futuro. Las predicciones se basanen modelos estadísticos como el ARIMA, que realiza una autorregresión sobre una media móvil. Por tanto, predice el valor esperado. Los valores reales observados están contenidos dentro de un intervalo de predicción del valor esperado. Este intervalo de predicción se calcula en función de la desviación típica. Por ejemplo, para un nivel de confianza del 95%, el intervalo de predicción está dentro de 1,96 desviaciones típicas del valor esperado. Además, las predicciones de varios pasos, que implican un horizonte de predicción más largo, también implican un intervalo de predicción mayor. Para saber más sobre series temporales, consulta el curso DataCamp sobre análisis de series temporales. 

Intervalo de confianza frente a intervalo de predicción: Un resumen

Los intervalos de confianza y los intervalos de predicción se utilizan a menudo en el mismo contexto, por lo que es importante entender en qué se diferencian. 

Esta tabla resume las diferencias basándose en el debate de las secciones anteriores:

Implementación de intervalos de confianza e intervalos de predicción en R

Esta sección muestra ejemplos prácticos del uso del lenguaje de programación R para estimar intervalos de confianza y de predicción. R es un lenguaje diseñado para aplicaciones estadísticas, y viene con conjuntos de datos y funciones estadísticas incorporadas. 

Para aprender más sobre regresiones utilizando R, sigue el tutorial de DataCamp sobre regresiones lineales en R.

Los ejemplos siguientes utilizan el conjunto de datos incorporado de Orange. Este conjunto de datos registra la circunferencia (en milímetros) y la edad (en días) de los naranjos. Naturalmente, cabe esperar que cuanto más viejo sea el árbol, mayor será su circunferencia. 

Implementar intervalos de confianza en R

Los ejemplos siguientes muestran cómo estimar intervalos de confianza para estadísticas de resumen y análisis de regresión. 

Intervalo de confianza en estadísticas de síntesis

Para obtener el intervalo de confianza de la media, ejecuta la prueba T estándar utilizando la función t.test() en el conjunto de datos:

t.test(Orange$circumference)

El resultado es como el del ejemplo siguiente:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0 
95 percent confidence interval:
   96.10926 135.60502 
sample estimates: 
mean of x
   115.8571 

Te da la estimación media y el intervalo de confianza del 95%. Por defecto, la función Prueba T utiliza un nivel de confianza del 95%. Utiliza el parámetro conf.level para especificar un intervalo de confianza diferente, como el 99%. 

> t.test(Orange$circumference, conf.level = 0.99)

Este comando produce el siguiente resultado:

t = 11.923, df = 34, p-value = 1.076e-13 
alternative hypothesis: true mean is not equal to 0
99 percent confidence interval:
   89.34458 142.36970 
sample estimates: 
mean of x
   115.8571 

Observa que la media estimada es la misma en ambos casos. Sin embargo, el intervalo debe ser más amplio para tener un mayor nivel de confianza. Basándome en los datos, tengo un 99% de seguridad de que la media está entre 89,3 y 142,4, pero sólo un 95% de seguridad de que está entre 96,1 y 135,6. Para un parámetro estimado a partir de una muestra dada, cuanto más estrecho sea el intervalo de confianza, menor será el nivel de confianza. 

Intervalo de confianza en la regresión 

En los análisis de regresión, necesitas los intervalos de confianza para los coeficientes de regresión y los valores predichos. 

Para conocer en profundidad cómo hacer regresiones en R, sigue el curso de DataCamp sobre Inferencia para la Regresión Lineal en R.

Intervalo de confianza de los coeficientes de regresión 

Los coeficientes de regresión se estiman analizando una muestra aleatoria. Por tanto, no son los verdaderos coeficientes de toda la población. Las estimaciones de los parámetros de regresión llevan asociados algunos errores. Además de sus valores estimados, es útil dar un intervalo de confianza para los parámetros. 

Utiliza la función lm() para construir un modelo lineal basado en el conjunto de datos Naranjos para predecir la circunferencia (en mm) de los naranjos dada su edad (en días):-

model_orange <- lm(circumference ~ age, data = Orange)

Comprueba los coeficientes de este modelo lineal:

model_orange

Este comando muestra los parámetros del modelo (intercepto y pendiente) como se indica a continuación:

Coefficients: (Intercept)          age
                              17.3997       0.1068  

Utiliza la función confint() para calcular los intervalos de confianza del 95%:

confint(model_orange, level = 0.95)

Ahora puedes ver los intervalos de confianza del 95% de la pendiente y el intercepto estimados por el modelo:

                          2.5 %                   97.5 %
(Intercept)     -0.14328303       34.9425835 
age                  0.08993141          0.1236092

Intervalo de confianza de una predicción de respuesta media 

Utiliza el modelo de regresión creado anteriormente para predecir la circunferencia media esperada de los árboles de 900 días. Utiliza el parámetro interval para especificar un intervalo de confianza. 

predict(model_orange, data.frame(age = 900), interval = "confidence", level = 0.95)  

La salida incluye la predicción (fit) y el intervalo de confianza (lwr y upr para los límites inferior y superior), como se muestra a continuación:

       fit                    lwr              upr
 1     113.4929        105.3211       121.6647

Implementar intervalos de predicción en R

Utiliza el mismo modelo anterior para predecir la circunferencia específica de un naranjo individual de 900 días. Utiliza el parámetro interval para especificar que quieres el intervalo de predicción. 

> predict(model, data.frame(age = 900), interval = "prediction", level = 0.95)  

El resultado se parece al ejemplo siguiente:

       fit                    lwr              upr
1      113.4929        64.5118        162.4741

Observa que, en ambos casos, el valor predicho de la circunferencia es el mismo: 113,49. Sin embargo, el intervalo de predicción es mucho más amplio que el intervalo de confianza. El intervalo de confianza de la predicción es el rango que se espera que contenga la circunferencia media de los árboles de 900 días. El intervalo de predicción es el rango esperado de la circunferencia de un árbol individual de 900 días. Esto se debe a que puede haber una variación considerablemente mayor en los árboles individuales, que se suaviza al considerar el valor medio. 

Errores y trampas habituales

Los intervalos estadísticos se utilizan habitualmente en campos de la estadística aplicada, como el análisis de datos, la farmacia, la econometría, etc. Para los que no tienen formación académica en estadística, es fácil confundir los intervalos de confianza y los intervalos de predicción. 

A continuación se exponen algunos errores comunes: 

• Hacer una predicción sin tener en cuenta el intervalo de predicción. 
• Cuando utilizas un modelo de regresión para predecir el valor de la variable dependiente para un valor dado de la variable independiente, la ecuación de regresión te da el valor esperado de la variable dependiente. El valor real rara vez coincide con el valor esperado, sino que se encuentra dentro de un determinado intervalo del valor esperado, especificado por el intervalo de predicción. 
• Suponiendo que un análisis de regresión sólo implique intervalos de predicción.
• Puedes hacer dos tipos de predicciones utilizando modelos de regresión: 1) predecir un valor futuro y 2) predecir la respuesta media. En el ejemplo del naranjo, puedes intentar predecir 1) la circunferencia de un naranjo concreto que tenga 900 días o 2) la circunferencia media de todos los árboles que tengan 900 días. En ambos casos, el valor esperado es el mismo. Sin embargo, el primero implica el intervalo de predicción, y el segundo, el intervalo de confianza. 
• Creer que el intervalo más estrecho es el mejor.
• A veces puedes tener la tentación de utilizar sólo el intervalo más estrecho al utilizar el resultado de un estudio de regresión. El intervalo de confianza no es de algún modo "mejor" porque sea más estrecho. Es más estrecho porque da el intervalo para algo distinto de lo que da el intervalo de predicción. Considera si intentas predecir el valor medio de la variable dependiente o si quieres predecir un punto de datos individual.
• Confundir un intervalo de confianza con un intervalo de predicción. 
• Si tu predicción implica determinar el valor de un parámetro poblacional a partir de una muestra o predecir la respuesta media (valor promedio) a partir de una regresión, utilizas el intervalo de confianza. Si intentas predecir alguna propiedad de un punto de datos individual basándote en una regresión, utiliza el intervalo de predicción. 

Conclusión

Este artículo ofrece una visión general de los intervalos de confianza y los intervalos de predicción. También explica la diferencia entre estos conceptos de apariencia similar y ofrece ejemplos prácticos de cuándo utilizar cada tipo de intervalo. El artículo también mostraba cómo calcular la predicción y los intervalos de confianza utilizando el lenguaje de programación R. 

Para aprender a aplicar fórmulas estadísticas utilizando Python, consulta el curso DataCamp sobre estadística en Python. Por último, si te estás preparando para entrevistas de trabajo relacionadas con la estadística, consulta el curso de DataCamp sobre preguntas para entrevistas de estadística en Python.