Média Winsorizada: Uma abordagem robusta para lidar com outliers

Os valores atípicos podem, muitas vezes, desviar suas percepções, transformando o que deveria ser uma análise significativa em uma conclusão enganosa. Dados imperfeitos e ruidosos são esperados em cenários do mundo real, e a winsorização é uma solução prática para reduzir o impacto dos outliers sem descartar nenhum dado.

Este artigo explorará como funciona a média winsorizada, suas aplicações práticas e as etapas para calculá-la usando Python. Também entenderemos seus prós e contras, compararemos com outras medidas úteis, como a média aparada, e exploraremos outras medidas estatísticas de winsorização.

O que é uma média winsorizada?

Uma média winsorizada é uma medida estatística que reduz o impacto dos outliers substituindo os valores extremos por percentis menos extremos em vez de removê-los completamente. Diferentemente da média aritmética, que considera todos os pontos de dados igualmente, a média winsorizada limita a influência de valores extremos que podem distorcer o resultado geral.

A Winsorização funciona limitando ou substituindo valores além de um determinado limite de percentil. Por exemplo, em uma winsorização de 5%, os 5% mais baixos dos pontos de dados são substituídos pelo valor no 5º percentil, e os 5% mais altos são substituídos pelo valor no 95º percentil. Esse método ajuda a reter a estrutura geral do conjunto de dados e, ao mesmo tempo, reduz o efeito de outliers, tornando-o uma alternativa robusta à média padrão em conjuntos de dados que contêm valores extremos.

Aplicações práticas da média winsorizada

A relevância da média winsorizada na análise estatística é particularmente evidente nos campos em que os dados são propensos a distribuições distorcidas. Aqui estão algumas áreas importantes em que a média winsorizada se mostra útil:

• Finanças e análise de investimentos: Os conjuntos de dados financeiros geralmente contêm valores extremos, como quedas de mercado ou ganhos excepcionais, que podem distorcer as médias e obscurecer as tendências. Os analistas podem produzir métricas de desempenho mais estáveis que reflitam melhor o comportamento típico do mercado por meio da winsorização dos retornos ou dos preços dos ativos.
• Dados econômicos: Em estudos macroeconômicos, indicadores como renda ou distribuição de riqueza são frequentemente distorcidos por um pequeno número de valores extremamente altos ou baixos. As médias winsorizadas podem fornecer uma visão mais equilibrada das condições econômicas, limitando a influência dessas observações extremas.
• Survey and Social Science Research: As pesquisas podem gerar dados com respostas extremas, como classificações muito altas ou muito baixas. Nesses casos, a média winsorizada fornece uma medida mais precisa da tendência central, garantindo que as respostas extremas não afetem desproporcionalmente a análise geral.
• Pesquisa médica e biológica: Os dados médicos, como resultados de pacientes ou resultados de testes, às vezes podem apresentar valores extremos devido a condições raras ou casos atípicos. A winsorização desses dados pode ajudar os pesquisadores a obter uma imagem mais precisa dos resultados médios sem remover completamente os pontos de dados potencialmente valiosos.

Em cada uma dessas aplicações, a média winsorizada é uma alternativa robusta à média padrão, permitindo que os analistas obtenham insights menos afetados por discrepâncias e preservem padrões de dados importantes.

Como calcular a média winsorizada em Python

O cálculo da média winsorizada em Python envolve a substituição dos valores extremos (outliers) por valores em percentis específicos. Antes de começar, um breve resumo das etapas que você seguirá:

• Importe as bibliotecas e o conjunto de dados necessários.

• Winsorize o conjunto de dados usando scipy.winsorize().

• Calcule a média usando numpy.mean().

Vamos nos aprofundar nos detalhes com um exemplo. 

Importe as bibliotecas e o conjunto de dados necessários

Primeiro, importaremos as bibliotecas necessárias para calcular a média.

import numpy as np
from scipy.stats.mstats import winsorize

Em seguida, carregamos o conjunto de dados, que pode ser de um arquivo CSV ou de qualquer outra fonte de dados. Para simplificar o exemplo, criaremos um conjunto de dados de amostra usando numpy.

data = np.array([10, 12, 14, 15, 16, 18, 20, 22, 24, 25, 30, 35, 40, 45, 50, 60, 70, 80, 82, 85, 90, 200])

O site 200 pode ser considerado uma exceção nesse conjunto de dados com base em uma análise inicial.

Winsorize o conjunto de dados 

A função winsorize() da biblioteca scipy permite que você especifique a porcentagem de dados a serem winsorizados a partir das caudas inferior e superior. O código para fazer isso é o seguinte:

# Winsorize 5% from both the lower and upper tails
winsorized_data = winsorize(data, limits=[0.05, 0.05])

No código acima, o parâmetro limits=[0.05, 0.05] fornecido à função winsorize() substitui os menores 5% e os maiores 5% dos valores pelos valores do 5º e 95º percentis, respectivamente. Agora podemos inspecionar os dados winsorizados que criamos.

print("Original data: ", data)
print("Winsorized data: ", winsorized_data)

O resultado mostrará que os valores discrepantes foram substituídos:

Original data: [ 10 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 200]
Winsorized data: [ 12 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 90]

Aqui, o valor máximo 200 foi substituído por 90; da mesma forma, os valores extremos da extremidade inferior, 10, foram substituídos por 12.

Calcule a média 

Por fim, vamos calcular a média dos dados winsorizados:

winsorized_mean = np.mean(winsorized_data)
print("Winsorized mean: ", winsorized_mean)

O resultado é o seguinte:

Winsorized mean: 42.5

A média winsorizada reduziu a influência dos valores extremamente altos em comparação com uma média regular. Para fins de comparação, podemos calcular a média original da seguinte forma:

original_mean = np.mean(data)
print("Original mean: ", original_mean)

O resultado é o seguinte:

Original mean: 47.40909090909091

Os outliers influenciam fortemente a média original em 47.40, fazendo com que ela seja significativamente maior. Após a winsorização dos valores extremos, a média winsorizada é muito menor em 42.5, com menor influência dos valores extremos.

Média Winsorizada vs. Média aparada: Principais diferenças

A média winsorizada e a média aparada são métodos estatísticos usados para reduzir o efeito de outliers na média, mas diferem na forma como lidam com valores extremos:

• A média Winsorized substitui os valores extremos (outliers) em ambas as extremidades dos dados pelos valores mais próximos dentro do conjunto de dados. Ele não descarta os dados, mas ajusta os valores mais extremos para reduzir seu impacto.
• A média aparada remove (apara) a porcentagem mais baixa e mais alta dos pontos de dados. Esse método descarta uma parte dos dados em ambas as extremidades. Em uma média aparada de 5%, os menores 5% e os maiores 5% dos pontos de dados são excluídos do cálculo da média.

A média winsorizada é preferível quando você deseja preservar a estrutura de dados (ou seja, manter o mesmo tamanho de amostra), mas ainda assim reduzir o efeito de valores extremos. A média aparada é preferível quando o conjunto de dados contém outliers claros que você deseja remover completamente e quando um tamanho de amostra menor após o corte é aceitável.

Comparando a média aparada e a média winsorizada em Python

Vamos ver como os dois métodos afetam o conjunto de dados e comparar seus resultados.

from scipy.stats import trim_mean

# Calculate the Trimmed mean by removing 5% from both tails
trimmed_mean = trim_mean(data, proportiontocut=0.05)

# Print the results
print("Original mean: ", np.mean(data))
print("Winsorized mean (5%): ", winsorized_mean)
print("Trimmed mean (5%): ", trimmed_mean)

O resultado é o seguinte:

Original mean: 47.40909090909091
Winsorized mean (5%): 42.5
Trimmed mean (5%): 41.65

A média original era 47.4, muito influenciada por outliers. A média winsorizada, 42.5, foi calculada com outliers substituídos por valores menos extremos. A média aparada, quando os outliers foram completamente removidos, é 41.65.

Saber quando usar cada método

Use a média winsorizada quando você quiser manter todos os pontos de dados, mas reduzir o impacto dos valores extremos. Essa é uma boa heurística porque a média winsorizada é útil quando você acredita que os valores discrepantes são genuínos, mas deseja minimizar sua influência.

Use a média aparada quando você quiser remover completamente os valores discrepantes do conjunto de dados. A média aparada é mais útil quando você suspeita que os valores discrepantes são errôneos ou não representativos da distribuição de dados.

Resumo das principais diferenças

As diferenças resumidas podem ser tabuladas conforme abaixo:

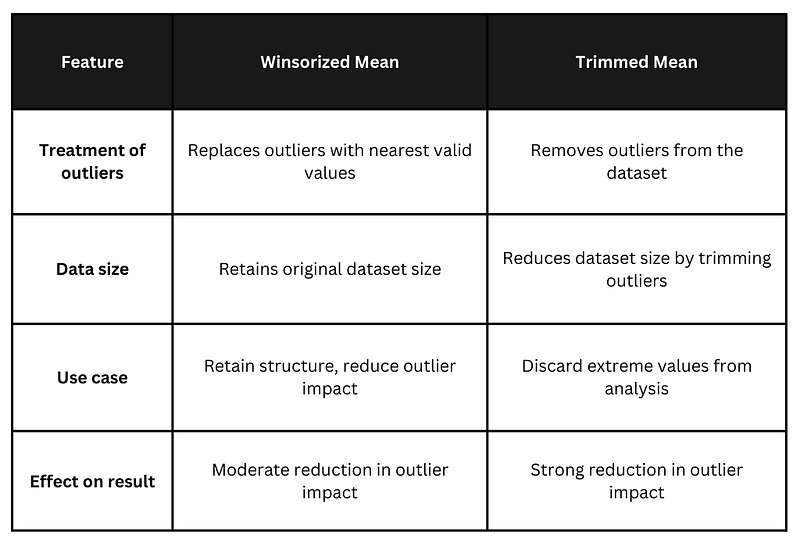entre Principais diferenças entre a média winsorizada e a média aparada. Imagem do autor.

As médias Winsorized e trimmed ajudam a lidar com outliers, mas a escolha depende de você querer reter ou descartar valores extremos do conjunto de dados.

Vantagens e desvantagens da média winsorizada

Embora o processo de winsorização seja uma abordagem robusta para lidar com outliers, a modificação de valores extremos pode gerar preocupações quanto à manipulação de dados. Aqui estão algumas vantagens e desvantagens da técnica:

Vantagens

• Mais robusto do que a média padrão na presença de valores discrepantes: A média winsorizada reduz o impacto de valores extremos (outliers), oferecendo uma tendência central mais estável e confiável em conjuntos de dados em que os outliers podem distorcer o resultado.
• Mantém a estrutura geral do conjunto de dados, mantendo todos os pontos de dados: Ao contrário da média aparada, que descarta os valores extremos, a média winsorizada os substitui por valores menos extremos, mantendo o tamanho da amostra e a estrutura geral do conjunto de dados.
• Mais adequado para pequenos conjuntos de dados: Para conjuntos de dados em que a remoção de pontos de dados (como no corte) resultaria em uma amostra não representativa ou incompleta, a winsorização preserva todos os valores, garantindo que o conjunto de dados permaneça utilizável.

Desvantagens

• Pode introduzir viés se a distribuição de dados subjacente for assimétrica: A miniaturização de dados com base em percentis fixos (por exemplo, 5% de ambas as extremidades) pode introduzir uma tendência se o conjunto de dados não for distribuído simetricamente. Se os dados forem distorcidos, a winsorização poderá distorcer a tendência central em vez de refleti-la com precisão.
• Requer uma seleção cuidadosa da porcentagem de winsorização: A porcentagem de dados a ser winsorizada (ou seja, a proporção de valores extremos a serem modificados) geralmente é escolhida arbitrariamente. A seleção de uma porcentagem inadequada pode não atenuar suficientemente o impacto dos valores discrepantes ou alterar muitos valores, reduzindo a representatividade do conjunto de dados.
• A supervalorização dos dados pode obscurecer padrões significativos: O excesso de distorção, ou a modificação de muitos pontos de dados, pode obscurecer padrões ou tendências significativas nos dados. Em alguns casos, os valores extremos representam informações válidas e vitais (por exemplo, em dados financeiros, em que os valores discrepantes podem significar eventos raros, mas impactantes), e substituí-los pode levar a conclusões enganosas.

Portanto, é importante considerar os prós e os contras do uso da técnica antes de incorporá-la aos nossos projetos de análise de dados.

Outros conceitos estatísticos com Winsorized

Como a winsorização é uma técnica estatística aplicada a uma medida, ela pode ser estendida a outras medidas estatísticas usuais. Vamos explorar algumas outras medidas às quais a winsorização pode ser aplicada:

• Desvio de amostra Winsorized: A versão winsorizada do desvio padrão mede a dispersão de um conjunto de dados winsorizados substituindo os valores extremos. Calculado como a raiz quadrada da variação Winsorizada.
• Variância winsorizada: A contrapartida winsorizada da variância mede o quanto os pontos de dados se desviam da média winsorizada, levando em conta a influência reduzida de outliers. É calculado como a média dos desvios ao quadrado da média winsorizada em um conjunto de dados winsorizados.
• Faixa winsorizada: A diferença entre os valores máximo e mínimo no conjunto de dados winsorizados, que é menor do que o intervalo original devido à substituição de outliers.
• Skewness Winsorized: Mede a assimetria da distribuição de um conjunto de dados winsorizados, indicando se a distribuição está inclinada para a esquerda ou para a direita após a winsorização. Ele ajuda a identificar a assimetria em conjuntos de dados em que valores extremos podem distorcer o cálculo padrão da assimetria.
• Correlação Winsorizada: Uma versão winsorizada da correlação de Pearson avalia a relação linear entre duas variáveis e, ao mesmo tempo, reduz o impacto dos outliers em ambos os conjuntos de dados.

Cada uma dessas medidas winsorizadas ajuda a reduzir a influência de outliers na análise ao trabalhar com dados não normais ou conjuntos de dados com valores extremos.

Conclusão

Este tutorial apresentou uma medida estatística para lidar com outliers: a média winsorizada. Aprendemos o conceito de winsorização, suas aplicações práticas e uma implementação prática em um conjunto de dados de amostra. Além disso, o tutorial abordou a média aparada, sua implementação e como ela difere da média winsorizada. Ele também explorou os prós, os contras e outros conceitos estatísticos baseados na winsorização. 

Como vimos, a média winsorizada equilibra o descarte de outliers e sua manutenção, permitindo resultados mais confiáveis em conjuntos de dados distorcidos. Incentivamos você a usar a técnica em seus projetos de análise de dados, experimentando diferentes níveis de winsorização para descobrir o que funciona melhor para conjuntos de dados específicos.

Confira nosso curso Intermediate Predictive Analytics in Python para saber mais sobre como lidar com outliers em conjuntos de dados usando Python, incluindo winsorização. Você também pode explorar nossa carreira de Cientista de Aprendizado de Máquina com Python, que é uma ótima maneira de praticar a criação de alguns modelos reais.