Winsorized Mean: A Robust Approach to Handling Outliers

Outliers can often misdirect your insights, turning what should be a meaningful analysis into a misleading conclusion. Imperfect and noisy data are expected in real-world scenarios, and winsorization is one practical solution to reduce the impact of outliers without discarding any data.

This article will explore how the winsorized mean works, its practical applications, and the steps to calculate it using Python. We’ll also understand its pros and cons, compare it with other useful measures such as trimmed mean, and explore other winsorization statistical measures.

What is a Winsorized Mean?

A winsorized mean is a statistical measure that reduces the impact of outliers by replacing extreme values with less extreme percentiles rather than completely removing them. Unlike the arithmetic mean, which considers all data points equally, the winsorized mean limits the influence of extreme values that can distort the overall result.

Winsorization works by capping or replacing values beyond a certain percentile threshold. For example, in a 5% winsorization, the lowest 5% of data points are replaced by the value at the 5th percentile, and the highest 5% are replaced by the value at the 95th percentile. This method helps retain the dataset’s overall structure while reducing the effect of outliers, making it a robust alternative to the standard mean in datasets that contain extreme values.

Practical applications of winsorized mean

The relevance of the winsorized mean in statistical analysis is particularly evident in fields where data is prone to skewed distributions. Here are some key areas where the winsorized mean proves helpful:

• Finance and Investment Analysis: Financial datasets often contain extreme values, such as market crashes or exceptional gains, which can distort averages and obscure trends. Analysts can produce more stable performance metrics that better reflect typical market behavior by winsorizing returns or asset prices.
• Economic Data: In macroeconomic studies, indicators like income or wealth distribution are frequently skewed by a small number of extremely high or low values. Winsorized means can provide a more balanced view of economic conditions by limiting the influence of these extreme observations.
• Survey and Social Science Research: Surveys can yield data with extreme responses, such as overly high or low ratings. In such cases, the winsorized mean provides a more accurate measure of central tendency, ensuring that extreme answers do not disproportionately affect the overall analysis.
• Medical and Biological Research: Medical data, such as patient outcomes or test results, can sometimes exhibit extreme values due to rare conditions or outlier cases. Winsorizing this data can help researchers obtain a more accurate picture of average outcomes without completely removing potentially valuable data points.

In each of these applications, the winsorized mean is a robust alternative to the standard mean, allowing analysts to gain insights less affected by outliers while preserving important data patterns.

How to Calculate the Winsorized Mean in Python

Calculating the winsorized mean in Python involves replacing the extreme values (outliers) with values at specific percentiles. Before starting, a quick summary of the steps we’ll follow:

• Import the required libraries and dataset.

• Winsorize the dataset using scipy.winsorize().

• Calculate the mean using numpy.mean().

Let’s dive into the details with an example. 

Import the required libraries and dataset

First, we shall import the libraries needed to calculate the mean.

import numpy as np
from scipy.stats.mstats import winsorize

Next, we load the dataset, which can be from a CSV file or any other data source. For the simplicity of the example, we shall create a sample dataset using numpy.

data = np.array([10, 12, 14, 15, 16, 18, 20, 22, 24, 25, 30, 35, 40, 45, 50, 60, 70, 80, 82, 85, 90, 200])

The 200 might be considered an outlier in this dataset based on an initial analysis.

Winsorize the dataset 

The winsorize() function from the scipy library allows you to specify the percentage of data to winsorize from both the lower and upper tails. The code to do so is as follows:

# Winsorize 5% from both the lower and upper tails
winsorized_data = winsorize(data, limits=[0.05, 0.05])

In the code above, the limits=[0.05, 0.05] parameter fed to the winsorize() function replaces the smallest 5% and largest 5% of values with the values at the 5th and 95th percentiles, respectively. We can now inspect the winsorized data we have created.

print("Original data: ", data)
print("Winsorized data: ", winsorized_data)

The output will show that the outliers have been replaced:

Original data: [ 10 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 200]
Winsorized data: [ 12 12 14 15 16 18 20 22 24 25 30 35 40 45 50 60 70 80 82 90 90]

Here, the maximum value 200 has been replaced with 90; similarly, extreme values from the lower end, 10, have been replaced by 12.

Calculate the mean 

Finally, let’s calculate the mean of the winsorized data:

winsorized_mean = np.mean(winsorized_data)
print("Winsorized mean: ", winsorized_mean)

The output is as follows:

Winsorized mean: 42.5

The winsorized mean has reduced the influence of the extremely high values compared to a regular mean. For comparison, we can calculate the original mean as follows:

original_mean = np.mean(data)
print("Original mean: ", original_mean)

The output is as follows:

Original mean: 47.40909090909091

The outliers heavily influence the original mean at 47.40, causing it to be significantly higher. After winsorizing the extreme values, the winsorized mean is much lower at 42.5 with lesser influence of the extreme values.

Winsorized Mean vs. Trimmed Mean: Key Differences

The winsorized mean and trimmed mean are both statistical methods used to reduce the effect of outliers on the mean, but they differ in how they handle extreme values:

• Winsorized mean replaces extreme values (outliers) at both ends of the data with the nearest values within the dataset. It doesn't discard data but instead adjusts the most extreme values to reduce their impact.
• Trimmed mean removes (trims) the lowest and highest percentage of data points. This method discards a portion of data at both ends. In a 5% trimmed mean, the smallest 5% and the largest 5% of data points are excluded from the mean calculation.

The winsorized mean is preferred when you want to preserve the data structure (i.e., keep the sample size the same) but still reduce the effect of extreme values. The trimmed mean is preferred when the dataset contains clear outliers you want to remove entirely and when a smaller sample size after trimming is acceptable.

Comparing trimmed mean and winsorized mean in Python

Let’s see how both methods affect the dataset and compare their results.

from scipy.stats import trim_mean

# Calculate the Trimmed mean by removing 5% from both tails
trimmed_mean = trim_mean(data, proportiontocut=0.05)

# Print the results
print("Original mean: ", np.mean(data))
print("Winsorized mean (5%): ", winsorized_mean)
print("Trimmed mean (5%): ", trimmed_mean)

The output is as follows:

Original mean: 47.40909090909091
Winsorized mean (5%): 42.5
Trimmed mean (5%): 41.65

The original mean was 47.4, heavily influenced by outliers. The winsorized mean, 42.5, was calculated with outliers replaced with less extreme values. The Trimmed mean, when the outliers were removed completely, is 41.65.

Knowing when to use each method

Use winsorized mean when you want to keep all the data points but reduce the impact of extreme values. This is a good heuristic because the winsorized mean is useful when you believe the outliers are genuine but want to minimize their influence.

Use the trimmed mean when you want to remove outliers from the dataset altogether. Trimmed mean is most useful when you suspect the outliers are erroneous or not representative of the data distribution.

Summary of key differences

The summarized differences can be tabulated as below:

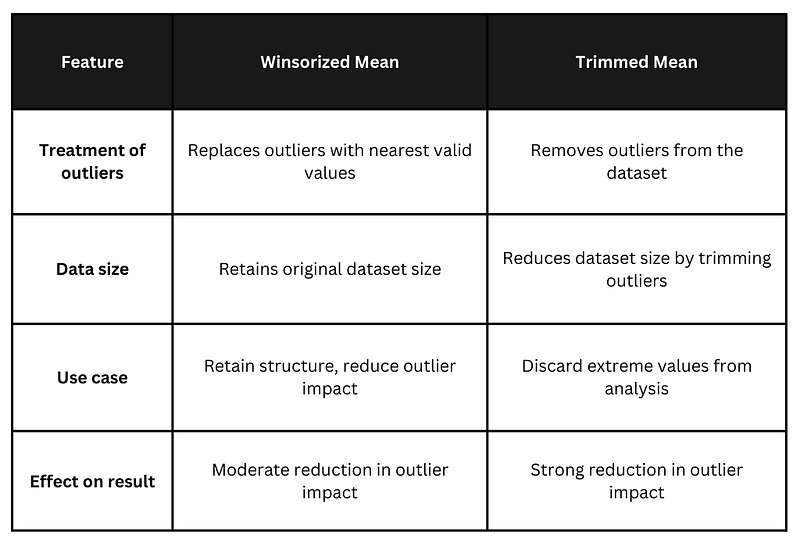Key differences between winsorized mean vs. trimmed mean. Image by Author.

Winsorized and trimmed means help handle outliers, but the choice depends on whether you want to retain or discard extreme values from the dataset.

Advantages and Drawbacks of Winsorized Mean

While the winsorization process is a robust approach to handling outliers, modifying extreme values might raise concerns about data manipulation. Here are some advantages and drawbacks of the technique:

Advantages

• More robust than the standard mean in the presence of outliers: The winsorized mean reduces the impact of extreme values (outliers), offering a more stable and reliable central tendency in datasets where outliers may distort the result.
• Retains the overall structure of the dataset by keeping all data points: Unlike the trimmed mean, which discards extreme values, the winsorized mean replaces them with less extreme values, maintaining the sample size and overall structure of the dataset.
• Better suited for small datasets: For datasets where removing data points (as in trimming) would result in an unrepresentative or incomplete sample, winsorization preserves all values, ensuring the dataset remains usable.

Drawbacks

• Can introduce bias if the underlying data distribution is asymmetric: Winsorizing data based on fixed percentiles (e.g., 5% from both ends) can introduce bias if the dataset is not symmetrically distributed. If the data is skewed, winsorization might distort the central tendency rather than accurately reflect it.
• Requires careful selection of the winsorization percentage: The percentage of data to winsorize (i.e., the proportion of extreme values to modify) is often chosen arbitrarily. Selecting an inappropriate percentage can either fail to sufficiently mitigate the impact of outliers or alter too many values, reducing the representativeness of the dataset.
• Over-winsorizing data may obscure significant patterns: Over-winsorizing, or modifying too many data points, can obscure meaningful patterns or trends in the data. In some cases, extreme values represent valid and vital information (e.g., in financial data, where outliers might signify rare but impactful events), and replacing them might lead to misleading conclusions.

Thus, it’s important to consider the pros and cons of using the technique before incorporating it into our data analysis projects.

Other Winsorized Statistical Concepts

Since winsorization is a statistical technique applied to a measure, it can be extended to other usual statistical measures. Let’s explore some other measures which winsorization can be applied to:

• Winsorized sample deviation: The winsorized version of the standard deviation measures the dispersion of a winsorized dataset by replacing extreme values. Calculated as the square root of the Winsorized variance.
• Winsorized variance: The winsorized counterpart of variance measures how much the data points deviate from the winsorized mean, accounting for reduced outlier influence. It’s calculated as the average squared deviations from the winsorized mean in a winsorized dataset.
• Winsorized range: The difference between the maximum and minimum values in the winsorized dataset, which is smaller than the original range due to the replacement of outliers.
• Winsorized skewness: Measures the asymmetry of a winsorized dataset’s distribution, indicating whether the distribution is skewed to the left or right after winsorization. It helps identify skewness in datasets where extreme values may distort the standard skewness calculation.
• Winsorized correlation: A winsorized version of Pearson's correlation assesses the linear relationship between two variables while reducing the impact of outliers in both datasets.

Each of these winsorized measures helps reduce the influence of outliers on the analysis when working with non-normal data or datasets with extreme values.

Conclusion

This tutorial introduced a statistical measure to handle outliers: the winsorized mean. We learned the concept of winsorization, its practical applications, and a hands-on implementation on a sample dataset. Further, the tutorial covered the trimmed mean, its implementation, and how it differs from the winsorized mean. It also explored the pros, cons, and other statistical concepts based on winsorization. 

As we have seen, winsorized mean balances discarding outliers and keeping them, allowing for more reliable results in skewed datasets. We encourage you to use the technique in your data analysis projects, experimenting with different winsorization levels to find what works best for specific datasets.

Check out our Intermediate Predictive Analytics in Python course to learn more about handling outliers in datasets using Python, including winsorization. You can also explore our Machine Learning Scientist with Python career track, which is a great way to practice by building some actual models.