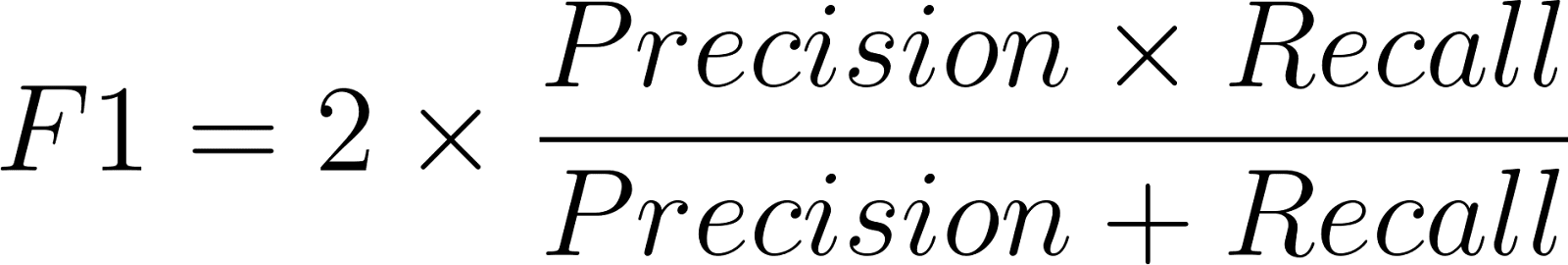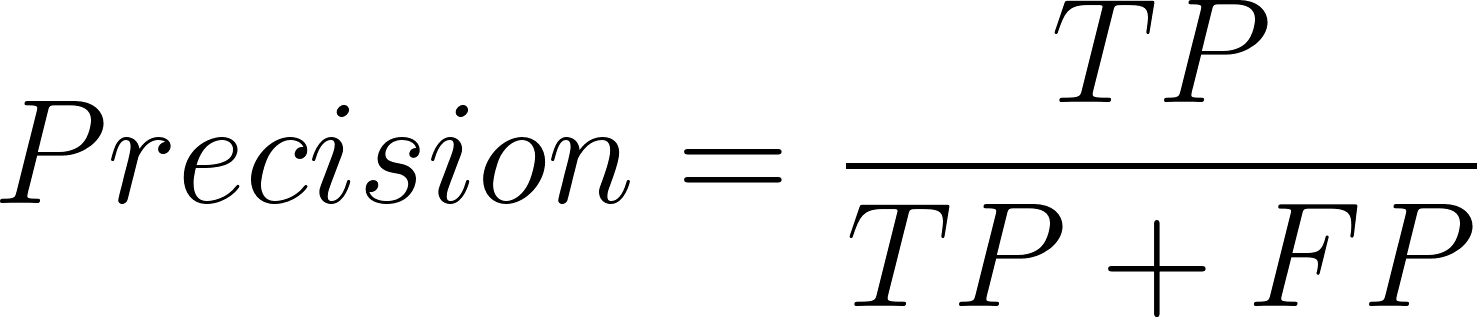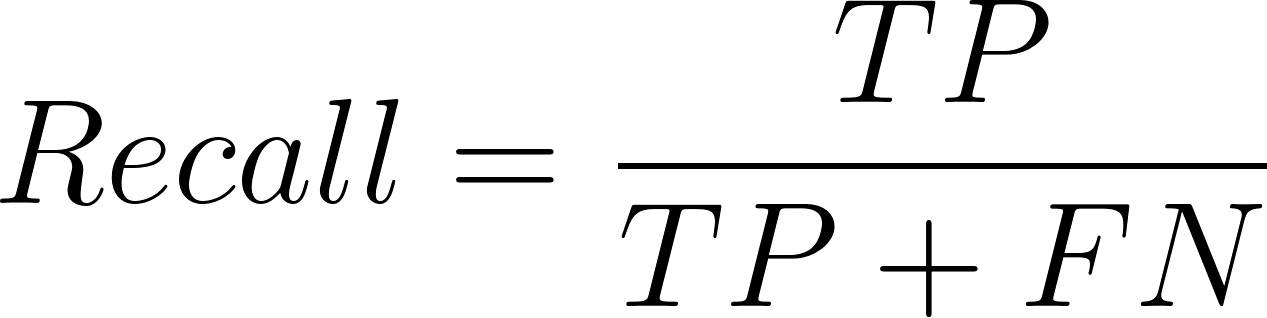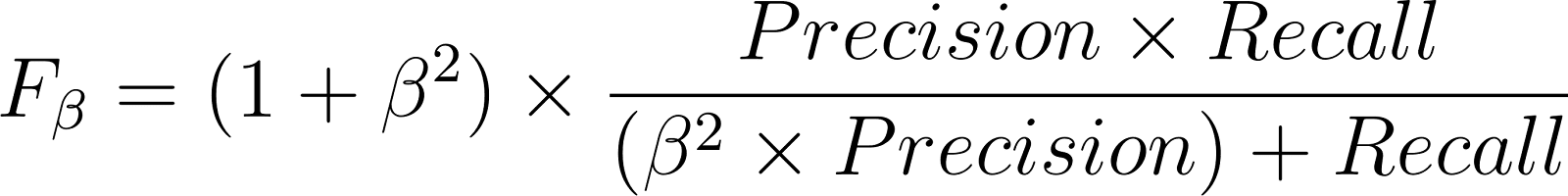Score F1 dans l'apprentissage automatique : Une mesure équilibrée de la précision et du rappel

Lors de la création de modèles basés sur le ML, l'évaluation des performances d'un modèle est tout aussi importante que son apprentissage. Bien que la précision soit souvent l'indicateur par défaut, elle peut être trompeuse, en particulier dans les ensembles de données déséquilibrés où une classe domine les données. 

Le score F1 est la moyenne harmonique de la précision et du rappel. Il équilibre le compromis entre les faux positifs et les faux négatifs, et fournit une mesure plus précise des performances du modèle.

Dans des applications telles que la détection des fraudes, le diagnostic médical, le filtrage des spams et la détection des défauts, la précision seule ne suffit pas pour donner une image complète de la situation. Un modèle peut atteindre un haut niveau de précision, mais s'il ne parvient pas à détecter de manière fiable les cas critiques rares, il pourrait causer plus de tort que de bien. Le score F1 tient compte de ce risque. Si vous débutez dans le domaine des mesures d'évaluation, nous vous recommandons de vous familiariser avec les concepts de base présentés dans la section Principes fondamentaux du machine learning en Python avant de poursuivre.

Qu'est-ce que le score F1 ?

Le score F1 évalue l'équilibre entre la précision et le rappel d'un modèle. Il varie de 0 à 1, où 1 indique une précision et un rappel parfaits, et 0 implique une performance médiocre.

• La précision permet d'évaluer, parmi toutes les prédictions positives du modèle, combien se sont avérées exactes.
• Le rappel est utile pour analyser combien ont été classés correctement par le modèle parmi tous les vrais positifs. 

Le score F1 combine les deux en un seul chiffre, pénalisant les modèles qui obtiennent de bons résultats sur l'un mais pas sur l'autre. Par exemple, un système qui mémorise très bien mais qui n'est pas très précis peut détecter correctement tous les cas positifs, mais donner trop de faux positifs. La mesure F1 garantit que les deux mesures sont prises conjointement. 

Formule et explication du score F1

La formule du score F1 est la suivante :

La précision est définie de la manière suivante :

Et l'équation pour le rappel est la suivante :

Ici, TP = vrais positifs, FP = faux positifs et FN = faux négatifs.

La moyenne harmonique est utilisée à la place de la moyenne arithmétique, car la première pénalise les différences importantes. En cas de haute précision mais de faible rappel (ou vice versa), le score F1 diminuera considérablement, reflétant un déséquilibre.

F1 Score par rapport à Précision

La précision détermine le nombre de prédictions correctes sur le nombre total de prédictions :

Bien qu'elle soit utile pour les ensembles équilibrés, la précision peut être trompeuse dans les problèmes déséquilibrés.

Exemple :

Si un système de filtrage anti-spam contient 90 % de spams et 10 % de messages non indésirables, un classificateur naïf qui classe tous les e-mails comme « spam » obtient une précision de 90 %, mais ne classe jamais correctement les e-mails non indésirables. Cela n'est pas utile dans la pratique.

Dans ce cas, la mesure F1 est plus précise, car elle tient compte du coût des faux positifs et des faux négatifs, ce que la précision ne fait pas.

Score F1 pour la classification binaire et multiclasses

Classification binaire

Dans la classification binaire, le score F1 est calculé par rapport à la classe positive. Par exemple, dans le cadre de tests médicaux, la classe positive pourrait représenter « la présence d'une maladie ».

Classification multiclasses

Dans les problèmes multiclasses, les scores F1 sont étendusà l'aide de méthodes de calcul de moyenne :

Cette flexibilité rend le score F1applicable à un large éventail de problèmes de classification.

Comment calculer le score F1 en Python

La bibliothèque scikit-learn comprend des fonctions simples permettant de calculer le score F1.

Exemple de classification binaire

Commencez par évaluer un problème de classification binaire simple où les prédictions sont soit 0, soit 1. La fonction f1_score() calcule directement le score F1 à l'aide des étiquettes réelles et prédites.

from sklearn.metrics import f1_score

# True labels
y_true = [0, 1, 1, 1, 0, 1, 0, 1]

# Predicted labels
y_pred = [0, 1, 0, 1, 0, 1, 1, 1]

# Calculate F1 Score
print("F1 Score:", round(f1_score(y_true, y_pred, average='binary'),2))

F1 Score: 0.8

Exemple de classification multiclasses

Ensuite, vous pouvez étendre cette approche aux problèmes multiclasses, où le modèle prédit plus de deux classes. Le paramètre « average » (agrégation des scores F1) contrôle la manière dont les scores F1 sont agrégés entre les classes. Les options courantes sont « 'macro' » (agrégation par classe), « 'micro' » (agrégation par score) et « 'weighted' » (agrégation par score et classe).

from sklearn.metrics import f1_score, classification_report

y_true = [0, 1, 2, 2, 0, 1, 2, 1, 2]
y_pred = [0, 2, 1, 2, 0, 0, 2, 1, 2]

# Macro, Micro, Weighted F1
print("Macro F1:", round(f1_score(y_true, y_pred, average='macro'),2))
print("Micro F1:", round(f1_score(y_true, y_pred, average='micro'),2))
print("Weighted F1:", round(f1_score(y_true, y_pred, average='weighted'),2))

# Detailed report
print(classification_report(y_true, y_pred))

Macro F1: 0.65
Micro F1: 0.67
Weighted F1: 0.64
              precision    recall  f1-score   support

           0       0.67      1.00      0.80         2
           1       0.50      0.33      0.40         3
           2       0.75      0.75      0.75         4

    accuracy                           0.67         9
   macro avg       0.64      0.69      0.65         9
weighted avg       0.65      0.67      0.64         9

Lorsque nous calculons l'F1 e ou l'Fβ e dans le cadre d'une classification multi-classes ou multi-étiquettes, il est nécessaire de déterminer comment calculer la moyenne des scores entre les différentes classes. Le paramètre moyen dans scikit-learn propose plusieurs options :

• Le binaire est utilisé dans le cas de deux classes. Nous nous concentrons sur la classe positive et calculons principalement l' precision, l' recall et l' F1 pour cette classe.

• Micro implique d'agréger les contributions de toutes les classes, puis de les moyenniser afin de calculer la métrique moyenne. En pratique, il additionne le total des vrais positifs, des faux négatifs et des faux positifs dans toutes les classes, puis calcule la précision, le rappel et le F1 sur la base de ces sommes. Le micro-moyennage apporte une valeur ajoutée en permettant d'évaluer la performance globale indépendamment du déséquilibre des classes.

• Macro : Nous calculons la métrique pour chaque classe, puis nous en calculons la moyenne non pondérée. Cela ne garantit pas un traitement égalitaire de toutes les classes et est donc acceptable si toutes les classes ont la même importance, même si l'ensemble de données est déséquilibré.

• La pondération est similaire à la macro, mais n'accorde pas le même poids à chaque classe. Il pondère les scores en fonction du nombre d'instances réelles par classe. Cela signifie que les classes plus importantes ont plus de poids dans la note finale. La moyenne pondérée est utile lorsque nous recherchons une vision équilibrée sans ignorer la répartition des classes.

• Exemples : Il est utilisé dans les problèmes multi-étiquettes, où un échantillon peut appartenir à plusieurs classes. Ici, la métrique est calculée pour chaque instance, puis moyennée sur l'ensemble des instances.

Ces options de calcul de moyenne nous permettent d'adapter le score F1 ou Fβ au scénario du problème. Par exemple, si nous classons des maladies rares pour lesquelles les classes minoritaires revêtent une importance primordiale, la macro ou Fβ, où β > 1, serait appropriée. Cependant, si nous recherchons la précision pour toutes les classes, la moyenne micro ou pondérée fournit une image plus précise.

Pour des besoins plus complexes, scikit-learn propose également fbeta_score(), qui généralise F1. Une compréhension approfondie de ces outils d's fait partie intégrante du cursus de scientifique en apprentissage automatique avec Python.

Généralisation du score F1 avec le score Fβ

Le score Fβ généralise le score F1 en fonction de la priorité accordée à la précision ou au rappel :

•  𝛃 > 1 accorde plus d'importance au rappel.
•  𝛃 < 1 met davantage l'accent sur la précision.

Exemples

• Le score F2 s'applique aux diagnostics médicaux où passer à côté d'une maladie (faux négatif) est plus grave qu'une fausse alerte.
• Le score F0.5 est préférable dans le filtrage des spams, où les faux positifs (le fait de confondre des e-mails légitimes) sont plus coûteux.

Cas d'utilisation : Détection du diabète avec F1 par rapport à Précision

Supposons un ensemble de données médicales dans lequel seulement 5 % des patients sont réellement atteints de diabète. Un modèle qui a été formé pour la détection du diabète peut atteindre une précision de 95 %. Cependant, cette précision de 95 % peut être facilement obtenue en prédisant systématiquement « pas de diabète » pour tout le monde, ce qui rend ce modèle inefficace.

Utilisons plutôt le score F1 pour évaluer le modèle.

from sklearn.metrics import f1_score, fbeta_score, confusion_matrix

# Suppose these are results from a diabetes detection model
y_true = [0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1]  # true outcomes
y_pred = [0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1]  # model predictions

print("Accuracy:", round((sum([yt == yp for yt, yp in zip(y_true, y_pred)]) / len(y_true)),2))
print("F1 Score:", round(f1_score(y_true, y_pred),2))
print("F2 Score (recall-focused):", round(fbeta_score(y_true, y_pred, beta=2),2))

Accuracy: 0.88
F1 Score: 0.8
F2 Score (recall-focused): 0.71

Pourquoi choisir F1 ou F2 ici ?

• La précision est trompeuse en raison du déséquilibre important entre les classes.
• Le score F1 garantit que les faux positifs (classification erronée de patients normaux comme diabétiques) et les faux négatifs (non-diagnostic du diabète) sont pris en compte.

Dans ce cas d'utilisation, le rappel est important, car un diagnostic manqué peut avoir des conséquences considérables. Le score F2 est donc plus approprié, car il accorde une plus grande importance au rappel.

Cela démontre comment la famille de mesures F1 offre une évaluation plus pratique et plus utile que la précision dans les cas d'utilisation clinique.

Points à retenir

Le score F1 nous rappelle que l'évaluation d'un modèle ne se résume pas à un simple jeu de chiffres. Il s'agit en réalité de comprendre les compromis qui sous-tendent chaque prévision. Ceci est important car, dans les applications réelles, le fait de négliger un cas critique peut avoir des conséquences graves.

Au fur et à mesure que vous continuez à créer et à affiner vos modèles, développer une intuition pour les métriques telles que F1 vous aidera à faire des choix plus adaptés au contexte en matière de performances. Pour approfondir vos compétences dans l'application de ces concepts d's à des ensembles de données réels, veuillez consulter le cursus professionnel Machine Learning Scientist with Python, où vous apprendrez à évaluer, ajuster et déployer efficacement des modèles dans divers cas d'utilisation.