Moyenne arithmétique : Un outil fondamental pour l'analyse des données

La moyenne arithmétique, communément appelée "moyenne", est souvent le point de départ des statistiques descriptives. Il fournit une mesure rapide et intuitive de la tendance centrale, qui est un élément essentiel de l'interprétation des données dans tous les domaines. Si le concept peut sembler simple, la compréhension des nuances de la moyenne arithmétique peut révéler des informations réelles sur des tendances et des modèles de données plus complexes.

Cet article offre une vue d'ensemble de la moyenne arithmétique, couvrant sa formule, ses applications et des comparaisons avec d'autres types de moyennes. Nous examinerons les raisons pour lesquelles elle est fréquemment utilisée en économie, en science des données et au-delà, tout en discutant des scénarios dans lesquels d'autres mesures pourraient être plus appropriées.

Pour ceux qui découvrent les statistiques ou qui cherchent à consolider leurs connaissances, notre cours d'introduction aux statistiques constitue une excellente base. Notre aide-mémoire sur les statistiques descriptives contient également un glossaire utile des termes relatifs à ce sujet.

Qu'est-ce que la moyenne arithmétique ?

La moyenne arithmétique est la somme de tous les nombres d'un ensemble de données divisée par le nombre de ces nombres. Ce calcul simple en fait l'une des mesures de tendance centrale les plus intuitives et les plus utilisées.

Pour illustrer ce propos, prenons un exemple simple. Supposons que nous ayons trois nombres : 5, 10 et 15. Calculer leur moyenne arithmétique :

1. Faites la somme des chiffres : 5 + 10 + 15 = 30
2. Comptez les chiffres : Nous avons 3 numéros
3. Divisez la somme par le nombre : 30 ÷ 3 = 10

Ainsi, la moyenne arithmétique de 5, 10 et 15 est de 10.

Principales propriétés de la moyenne arithmétique

La moyenne arithmétique possède plusieurs propriétés importantes qui deviennent plus intrigantes après un examen plus approfondi. 

La somme des écarts est égale à zéro

Une propriété fondamentale de la moyenne arithmétique est que la somme des écarts par rapport à celle-ci est toujours égale à zéro. En d'autres termes, si vous soustrayez la valeur moyenne de chaque point de données et que vous additionnez ces différences, le résultat sera zéro. Mathématiquement, cela peut s'exprimer comme suit :

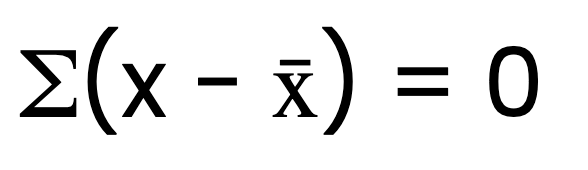
Où x représente chaque valeur de l'ensemble de données et x̄ est la moyenne arithmétique.

Sensibilité aux valeurs aberrantes

Dans les ensembles de données comportant des valeurs extrêmes, la moyenne arithmétique peut être sensiblement rapprochée de ces valeurs aberrantes, ce qui peut conduire à des interprétations trompeuses, en particulier dans le cas de distributions asymétriques. Par exemple, considérons un ensemble de données sur les salaires dans une petite entreprise : {$30,000, $35,000, $40,000, $45,000, $1,000,000}. La moyenne arithmétique (230 000 $) est nettement plus élevée que la plupart des salaires en raison de la valeur aberrante de 1 000 000 $.

Cette sensibilité rend la moyenne arithmétique moins robuste que des mesures telles que la médiane en présence de valeurs aberrantes ou pour des distributions asymétriques. Cependant, la moyenne peut également être utile pour détecter la présence de valeurs aberrantes ou pour comprendre l'impact des valeurs extrêmes sur un ensemble de données.

Impact des changements de données

La moyenne arithmétique réagit de manière prévisible aux changements dans l'ensemble des données, ce qui peut être utile dans divers scénarios analytiques :

1. Ajout ou soustraction d'une constante: Si vous ajoutez ou soustrayez la même valeur à chaque point de données, la moyenne augmentera ou diminuera d'autant. Par exemple, si vous ajoutez 5 à chaque valeur d'un ensemble de données, la nouvelle moyenne sera supérieure de 5 à la moyenne initiale.
2. Multiplier ou diviser par une constante: Si vous multipliez ou divisez chaque point de données par la même constante non nulle, la moyenne sera multipliée ou divisée par cette constante. Par exemple, si vous doublez chaque valeur d'un ensemble de données, la nouvelle moyenne sera le double de la moyenne initiale.

Ces propriétés rendent la moyenne arithmétique particulièrement utile dans les scénarios impliquant des changements uniformes dans un ensemble de données, comme l'ajustement de l'inflation dans les données économiques ou la mise à l'échelle des mesures dans les expériences scientifiques.

Quand utiliser la moyenne arithmétique

La moyenne arithmétique est un outil statistique polyvalent, mais elle est particulièrement efficace dans certains cas. Il convient tout d'abord de préciser que la moyenne arithmétique est particulièrement utile pour les ensembles de données impliquant des processus additifs. Par exemple, si vous calculez la température moyenne journalière, le salaire moyen dans une entreprise ou les résultats moyens à un examen, la moyenne arithmétique fournit une représentation significative de la valeur centrale.

Il convient également de préciser que la moyenne arithmétique est la plus fiable lorsque les données sont uniformément réparties et qu'il n'y a pas de valeurs extrêmes aberrantes. la plus fiable lorsque les points de données sont uniformément répartis et qu'il n'y a pas de valeurs extrêmes aberrantes. Examinons quelques exemples spécifiques à l'industrie :

• Finances : Dans le domaine financier, les entreprises s'appuient sur la moyenne arithmétique pour obtenir des informations et fixer des repères. Par exemple, les entreprises l'utilisent pour déterminer les salaires moyens, les dépenses mensuelles et les bénéfices trimestriels.
• L'économie : Les économistes utilisent la moyenne arithmétique pour analyser les tendances de la consommation et la stabilité des prix. Parmi les principales applications, citons le calcul de la consommation moyenne des ménages et l'élaboration d'indices tels que l'indice des prix à la consommation (IPC) pour suivre l'évolution de l'inflation dans le temps.
• Soins de santé et recherche médicale : Dans le domaine de la santé, la moyenne arithmétique joue un rôle essentiel dans l'évaluation des traitements et l'étude des tendances en matière de santé. Par exemple, les chercheurs calculent les délais de guérison moyens et l'efficacité des médicaments, tandis que les épidémiologistes évaluent les taux d'infection moyens et les délais de survie.

Comment calculer la moyenne arithmétique ?

Nous avons déjà abordé le concept de base, mais nous allons voir comment calculer la moyenne arithmétique à l'aide d'outils tels que R, Python et Excel, ce qui est pratiquement indispensable. comme R, Python et Excel, ce qui est pratiquement nécessaire pour les grands ensembles de données.

Formule de la moyenne arithmétique

La formule de la moyenne arithmétique est la suivante :

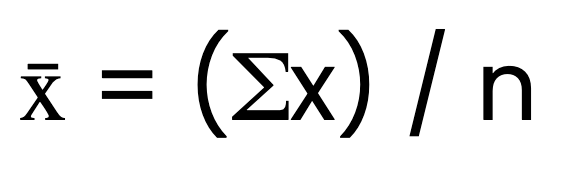
Où x̄ est la moyenne arithmétique, Σx est la somme de toutes les valeurs et n est le nombre de valeurs.

Moyenne arithmétique dans Excel, Python et R

Pour les grands ensembles de données, les outils logiciels facilitent grandement les calculs. Voici comment calculer la moyenne arithmétique dans Excel, Python et R. 

Excel

Dans Excel, vous pouvez utiliser la fonction AVERAGE():

1. Saisissez vos données dans une colonne ou une ligne.

2. Dans une nouvelle cellule, tapez =AVERAGE().

3. Sélectionnez la plage de cellules contenant vos données.

4. Fermez la parenthèse et appuyez sur Entrez dans le menu.

Par exemple, si vos données se trouvent dans les cellules A1:A10, vous utiliserez : =AVERAGE(A1:A10).

Python

Le module de statistiques de Python propose une fonction mean():

from statistics import mean

data = [5, 10, 15, 20, 25]

result = mean(data)
print(result)  # Output: 15

Pour les grands ensembles de données, vous préférerez peut-être la fonction mean() de NumPy, plus efficace :

import numpy as np

data = np.array([5, 10, 15])

result = np.mean(data)
print(result)  # Output: 10.0

R

Dans R, vous pouvez utiliser la fonction mean() intégrée à la base R :

data <- c(5, 10, 15)

result <- mean(data)
print(result)  # Output: [1] 10

Ces outils rationalisent le processus de calcul de la moyenne arithmétique pour des ensembles de données de toute taille, vous permettant de vous concentrer sur l'interprétation des données plutôt que sur le calcul manuel.

Moyenne arithmétique en science des données, apprentissage automatique et statistiques

Les applications de la moyenne arithmétique en science des données et en apprentissage automatique vont du prétraitement des données à l'évaluation des modèles. Examinons quelques domaines clés où la moyenne arithmétique est particulièrement importante. 

Mise à l'échelle des fonctionnalités

L'une des applications les plus courantes de la moyenne arithmétique dans le prétraitement des données est la mise à l'échelle des caractéristiques, en particulier le centrage moyen :

• Centrage moyen: Ce processus consiste à soustraire la moyenne arithmétique de chaque point de données d'une caractéristique. Le résultat est un ensemble de données centrées où la moyenne de chaque caractéristique est égale à zéro. Elle peut être représentée comme suit : x_centered = x - x̄ où x est la valeur originale et x̄ est la moyenne arithmétique de la caractéristique.

• Normalisation: Souvent utilisée en conjonction avec le centrage sur la moyenne, la normalisation consiste à diviser par l'écart type après avoir soustrait la moyenne : x_standardized = (x - x̄) / σ où σ est l'écart-type de la caractéristique.

Ces techniques permettent de normaliser l'échelle des caractéristiques, ce qui est particulièrement important pour de nombreux algorithmes d'apprentissage automatique. Si vous souhaitez en savoir plus sur la différence entre normalisation et standardisation, vous pouvez consulter le tutoriel complet.

Évaluation du modèle

La moyenne arithmétique est fondamentale dans diverses mesures d'évaluation de modèles :

• Erreur quadratique moyenne (EQM): Cette mesure courante pour les problèmes de régression calcule la moyenne des différences au carré entre les valeurs prédites et les valeurs réelles.
• Erreur absolue moyenne (MAE): Similaire à l'EQM, mais utilise la différence absolue au lieu de la différence au carré.
• Précision: Dans les problèmes de classification, la précision est souvent indiquée comme la moyenne des prédictions correctes sur l'ensemble des échantillons.

Statistiques et tests d'hypothèses

En analyse statistique, la moyenne arithmétique est souvent utilisée dans les tests d'hypothèse. Par exemple :

• Tests T : La moyenne arithmétique est essentielle dans les tests t, qui comparent les moyennes de deux groupes pour déterminer si elles sont statistiquement différentes. En comparant les moyennes des échantillons, les tests t permettent de valider des hypothèses sur les caractéristiques de la population.
• Intervalles de confiance: La moyenne arithmétique est utilisée pour calculer les intervalles de confiance, qui indiquent la fiabilité de la moyenne estimée. Cela permet de savoir dans quelle mesure la moyenne de l'échantillon est représentative de l'ensemble de la population.

Autres applications

• Méthodes d'ensemble: De nombreuses techniques d'ensemble, telles que le bagging et le boosting, utilisent la moyenne arithmétique pour combiner les prédictions de plusieurs modèles.
• Descente en gradient: La moyenne arithmétique est utilisée pour calculer le gradient moyen des mini-lots dans la descente de gradient stochastique.
• Détection des anomalies: Les écarts par rapport à la moyenne peuvent être utilisés pour identifier les valeurs aberrantes ou les anomalies dans les ensembles de données. Par exemple, une heuristique courante consiste à utiliser trois écarts types comme seuil, de sorte que tout point de données s'écartant de trois écarts types ou plus de la moyenne arithmétique soit considéré comme une valeur aberrante.
• Réduction de la dimensionnalité: Des techniques telles que l'analyse en composantes principales (ACP) utilisent la moyenne arithmétique dans leurs calculs pour centrer les données avant de calculer la matrice de covariance.
• Réseaux neuronaux: Dans l'algorithme de rétropropagation, la moyenne arithmétique est utilisée pour calculer l'erreur moyenne sur l'ensemble des exemples d'apprentissage.
• Validation croisée: Lors de la validation croisée k-fold, la moyenne arithmétique des mesures de performance sur l'ensemble des plis est généralement présentée comme l'estimation de la performance globale.

Comme vous le remarquez peut-être, la moyenne arithmétique est importante à la fois pour l'interprétation des résultats des données et pour l'étape de prétraitement nécessaire à la performance optimale du modèle. Pour approfondir votre compréhension de ces concepts et de leurs applications pratiques, envisagez de suivre notre cursus professionnel Machine Learning Scientist in Python, qui couvre ces sujets de manière plus approfondie.