Élimination de la gaussienne : Une méthode pour résoudre les systèmes d'équations

L'élimination gaussienne est l'un des algorithmes les plus fondamentaux de l'algèbre linéaire pour résoudre les systèmes d'équations linéaires. Nommée d'après le mathématicien allemand Carl Friedrich Gauss, cette méthode transforme un système d'équations en une forme équivalente plus simple en effectuant une séquence d'opérations sur sa représentation matricielle.

Dans cet article, nous allons explorer le fonctionnement de l'élimination gaussienne, la mettre en œuvre en Python et examiner ses applications en science des données et en calcul numérique. En comprenant cet algorithme, nous aurons un aperçu d'une technique fondamentale qui sous-tend de nombreuses méthodes de calcul utilisées dans l'analyse des données.

Qu'est-ce que l'élimination gaussienne ?

L'élimination gaussienne est un algorithme permettant de résoudre des systèmes d'équations linéaires en transformant systématiquement la matrice augmentée du système en forme d'échelon de rangée (REF). Cette transformation préserve l'ensemble des solutions tout en facilitant la recherche des valeurs des variables.

Une matrice est sous forme d'échelon de rangée lorsque :

• Toutes les lignes entièrement composées de zéros se trouvent au bas de la matrice.
• L'entrée principale (premier élément non nul) de chaque ligne non nulle se trouve à droite de l'entrée principale de la ligne qui la précède.
• Tous les éléments situés en dessous d'une entrée principale sont des zéros.

Pour obtenir la forme échelon de rangée, nous utilisons trois types d'opérations élémentaires sur les rangées :

• Permutation des rangs : Échanger deux lignes
• Échelonnement des rangs : Multiplier tous les éléments d'une ligne par une constante non nulle
• Ajout d'une rangée : Remplacer une ligne par la somme d'elle-même et d'un multiple d'une autre ligne

En outre, il est important de faire la distinction entre l'élimination gaussienne et l'élimination de Gauss-Jordan :

• L'élimination gaussienne transforme la matrice en forme d'échelon de rangée, ce qui nécessite une rétro-substitution pour trouver les valeurs des variables.
• L'élimination de Gauss-Jordan poursuit le processus pour réduire la forme échelon ligne (RREF), où toutes les entrées principales sont 1 et toutes les autres entrées dans la colonne de chaque entrée principale sont 0.

Bien que l'élimination de Gauss-Jordan fournisse une solution plus directe, l'élimination gaussienne est généralement plus efficace pour les systèmes de grande taille, en particulier lorsqu'elle est combinée à la rétrosubstitution et à des techniques telles que la décomposition LU.

Décomposition étape par étape de l'algorithme d'élimination de la gaussienne

Examinons le processus d'élimination gaussienne à l'aide d'un exemple simple. Considérez le système d'équations linéaires suivant :

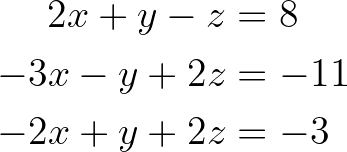
Système d'équations linéaires. Image par l'auteur.

Étape 1 : Créer la matrice augmentée

Tout d'abord, nous représentons le système sous la forme d'une matrice augmentée, en combinant la matrice des coefficients avec les constantes :

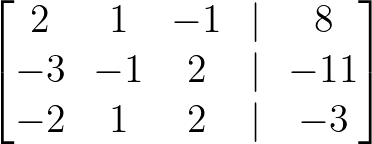
Matrice augmentée. Image par l'auteur.

Étape 2 : Élimination anticipée

Nous allons maintenant effectuer des opérations élémentaires sur les lignes pour transformer la matrice en forme d'échelon de ligne.

Faites du premier élément de la première colonne un pivot et éliminez tous les éléments situés en dessous :

• Ajoutez 3/2 × rang 1 au rang 2 :

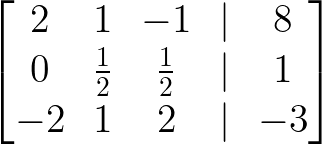
Ajoutez 3/2 × rang 1 au rang 2. Image par l'auteur.

• Ajoutez le rang 1 au rang 3 :

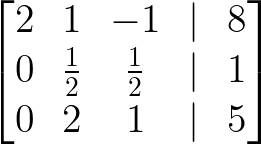
Ajoutez le rang 1 au rang 3. Image par l'auteur.

Passez à la deuxième colonne et éliminez tous les éléments situés sous le pivot :

• Multipliez la rangée 2 par 2 pour obtenir le pivot 1 :

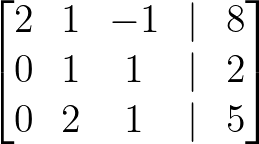
Multipliez le rang 2 par 2. Image par l'auteur.

• Soustrayez 2 × rangée 2 de la rangée 3 :

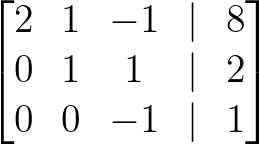
Soustrayez 2 × rang 2. Image par l'auteur.

Faites en sorte que le pivot de la troisième ligne soit positif :

• Multipliez le rang 3 par -1 :

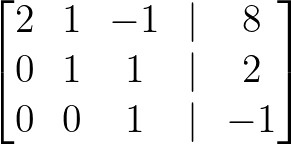
Multipliez le rang 3 par -1. Image par l'auteur.

La matrice est maintenant sous forme d'échelon de rangée.

Étape 3 : Substitution en arrière

Nous pouvons maintenant trouver les valeurs de nos variables par rétro-substitution :

A partir du rang 3 : 

          z = -1

A partir du rang 2 : 

          y + z = 2,

          donc y + (-1) = 2,

          ce qui donne y = 3

A partir du rang 1 : 

          2x + y - z = 8,

          donc 2x + 3 - (-1) = 8,

          ce qui donne 2x = 4,

          so x = 2

La solution est donc x = 2, y = 3, z = -1.

Bien que nous appliquions l'élimination gaussienne à cet exemple, les étapes restent les mêmes pour un autre système d'équations linéaires.

Mise en œuvre de l'élimination gaussienne en Python

Bien que nous puissions écrire l'algorithme à l'aide de Python de base, les opérations vectorisées de NumPy rendent l'implémentation à la fois plus propre et nettement plus rapide. 

À des fins éducatives, il est utile de comprendre l'algorithme sous-jacent, mais pour une utilisation en production, il est recommandé d'utiliser des bibliothèques optimisées. Ayant déjà compris l'algorithme sous-jacent dans la section précédente, nous allons maintenant nous plonger dans la mise en œuvre à l'aide de bibliothèques optimisées en Python.

Mise en œuvre basée sur NumPy

NumPy fournit la fonction numpy.linalg.solve(), qui met en œuvre une solution hautement optimisée pour les systèmes d'équations linéaires :

import numpy as np

# Define the coefficient matrix A and constant vector b
A = np.array([[2, 1, -1],
             [-3, -1, 2],
             [-2, 1, 2]], dtype=float)
b = np.array([8, -11, -3], dtype=float)

# Solve the system Ax = b
x = np.linalg.solve(A, b)

print("Solution:", x)

Dans le code ci-dessus, nous définissons la matrice des coefficients A, ainsi que le vecteur constant b, comme la matrice augmentée que nous avons créée à l'étape 1 de l'exemple d'élimination gaussienne ci-dessus. 

Nous utilisons la fonction numpy.linalg.solve()pour obtenir la solution et nous imprimons la sortie comme indiqué ci-dessous :

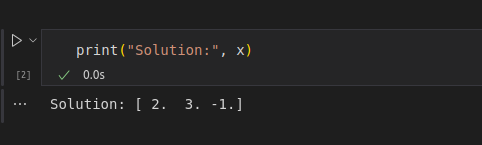
Solution à l'aide d'un code de mise en œuvre. Image par l'auteur.

Cette implémentation utilise LAPACK sous le capot, qui applique la décomposition LU (une variante de l'élimination gaussienne) optimisée pour la stabilité numérique et la performance.

Traitement des cas particuliers

Lors de la mise en œuvre de l'élimination gaussienne, vous rencontrerez plusieurs cas particuliers qui devront être traités avec soin :

• Matrices singulières: Si le déterminant de votre matrice de coefficients est nul ou très proche de zéro, le système n'a pas de solution ou en a une infinité. La fonction linalg.solve() de NumPy soulève un LinAlgError dans ce cas.

• Stabilité numérique: Avec l'arithmétique à virgule flottante, les erreurs d'arrondi peuvent s'accumuler et conduire à des résultats inexacts. Le pivotement partiel, où l'élément le plus grand d'une colonne est sélectionné comme pivot, permet d'atténuer ce problème.

• Systèmes surdéterminés ou sous-déterminés: Lorsque le nombre d'équations ne correspond pas au nombre de variables, vous pouvez utiliser numpy.linalg.lstsq(), qui trouve la solution la plus simple.

Pour les grands systèmes comportant de nombreux zéros, les solveurs de matrices éparses de SciPy peuvent être des ordres de grandeur plus rapides que les solveurs denses :

from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

# For large sparse matrices
A_sparse = csr_matrix(A)
x = spsolve(A_sparse, b)

Bien qu'il soit utile de comprendre les mécanismes de l'algorithme, en pratique, l'utilisation des implémentations optimisées de NumPy et SciPy vous permet de résoudre des systèmes linéaires de manière efficace et fiable sans avoir à réinventer la roue.

Utilisation de l'élimination gaussienne

L'élimination gaussienne va bien au-delà des mathématiques théoriques et trouve de nombreuses applications pratiques dans divers domaines de la science, de l'ingénierie et de l'analyse de données. 

Voici quelques-unes des applications les plus importantes de cet algorithme fondamental dans le monde réel :

• Régression linéaire: En science des données, l'élimination gaussienne est utilisée pour résoudre les équations normales qui apparaissent lors de la recherche des paramètres les mieux adaptés dans les modèles de régression linéaire. Cela permet aux analystes de faire des prévisions sur la base de données historiques.
• Analyse de réseau: Les ingénieurs utilisent l'élimination gaussienne pour résoudre des courants ou des tensions inconnus dans les circuits électriques en appliquant les lois de Kirchhoff, qui génèrent des systèmes d'équations linéaires qui doivent être résolus simultanément.
• Inversion de matrice: L'élimination gaussienne constitue la base du calcul des inversions de matrices, qui sont essentielles dans les transformations, les analyses statistiques et la résolution de problèmes mathématiques complexes dans les algorithmes d'apprentissage automatique.
• Intégration numérique: Lors de la mise en œuvre de méthodes numériques avancées telles que les schémas d'intégration implicites d' Euler ou de Runge-Kutta, l'élimination gaussienne est utilisée pour résoudre les systèmes d'équations résultants, ce qui garantit la stabilité des simulations de systèmes dynamiques.

En comprenant ces applications, nous pouvons voir comment une simple technique mathématique peut servir d'épine dorsale à de nombreux outils utilisés quotidiennement par les data scientists, les ingénieurs et les chercheurs.

Conclusion

Cet article explore l'algorithme fondamental de l'élimination gaussienne pour résoudre les systèmes d'équations linéaires en transformant les matrices en forme d'échelon de rangée. Nous avons également appris à mettre en œuvre cette technique en Python à l'aide des fonctions optimisées de NumPy, et nous avons compris ses applications pratiques dans la régression linéaire, l'analyse de réseau, l'inversion de matrice et les méthodes numériques. 

Pour approfondir votre connaissance de l'algèbre linéaire et de ses applications en science des données, pensez à vous inscrire à notre cours d'algèbre linéaire, où vous explorerez des concepts plus avancés et des implémentations de ces techniques fondamentales.