Eliminação Gaussiana: Um método para resolver sistemas de equações

A eliminação gaussiana é um dos algoritmos mais fundamentais da álgebra linear para resolver sistemas de equações lineares. Nomeado em homenagem ao matemático alemão Carl Friedrich Gauss, esse método transforma um sistema de equações em uma forma equivalente e mais simples, executando uma sequência de operações em sua representação matricial.

Neste artigo, você verá como funciona a eliminação gaussiana, como implementá-la em Python e como examinar suas aplicações em ciência de dados e computação numérica. Ao compreender esse algoritmo, você terá uma visão de uma técnica fundamental que está na base de muitos métodos computacionais usados na análise de dados.

O que é eliminação gaussiana?

A eliminação gaussiana é um algoritmo para resolver sistemas de equações lineares transformando sistematicamente a matriz aumentada do sistema em uma forma de escalonamento de linhas (REF). Essa transformação preserva o conjunto de soluções e, ao mesmo tempo, facilita a localização dos valores das variáveis.

Uma matriz está na forma escalonada quando:

• Todas as linhas que consistem inteiramente de zeros estão na parte inferior da matriz
• A entrada principal (primeiro elemento diferente de zero) de cada linha diferente de zero está à direita da entrada principal da linha acima dela
• Todos os elementos abaixo de uma entrada inicial são zeros

Para obter a forma escalonada de linha, usamos três tipos de operações elementares de linha:

• Troca de linha: Trocar duas linhas
• Escalonamento de fileiras: Multiplicar todos os elementos em uma linha por uma constante diferente de zero
• Adição de linha: Substituir uma linha pela soma dela mesma e um múltiplo de outra linha

Além disso, é importante distinguir entre a eliminação Gaussiana e a eliminação Gauss-Jordan:

• Eliminação gaussiana transforma a matriz em uma forma escalonada de linhas, exigindo a substituição reversa para encontrar valores de variáveis
• Eliminação de Gauss-Jordan continua o processo para reduzir a forma escalonada de linha (RREF), em que todas as entradas principais são 1 e todas as outras entradas na coluna de cada entrada principal são 0

Embora a eliminação de Gauss-Jordan ofereça uma solução mais direta, a eliminação gaussiana geralmente é mais eficiente para sistemas grandes, especialmente quando combinada com a substituição reversa e técnicas como a decomposição LU.

Detalhamento passo a passo do algoritmo de eliminação gaussiana

Vamos examinar o processo de eliminação gaussiana usando um exemplo simples. Considere o seguinte sistema de equações lineares:

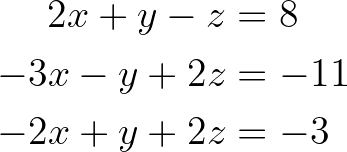
Sistema de equações lineares. Imagem do autor.

Etapa 1: Criar a matriz aumentada

Primeiro, representamos o sistema como uma matriz aumentada, combinando a matriz de coeficientes com as constantes:

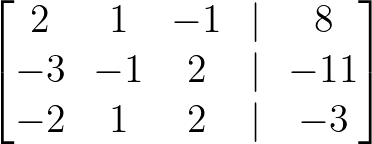
Matriz aumentada. Imagem do autor.

Etapa 2: Eliminação direta

Agora, realizaremos operações elementares de linha para transformar a matriz na forma de escalonamento de linha.

Faça com que o primeiro elemento da primeira coluna seja um pivô e elimine todos os elementos abaixo dele:

• Adicione 3/2 × linha 1 à linha 2:

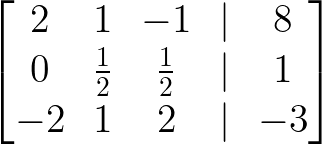
Adicione 3/2 × linha 1 à linha 2. Imagem do autor.

• Adicione a linha 1 à linha 3:

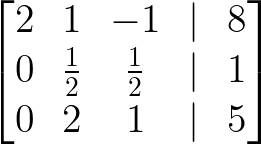
Adicione a linha 1 à linha 3. Imagem do autor.

Vá para a segunda coluna e elimine todos os elementos abaixo do pivô:

• Multiplique a linha 2 por 2 para obter o pivô 1:

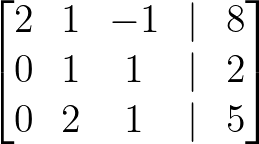
Multiplique a linha 2 por 2. Imagem do autor.

• Subtraia 2 × Linha 2 da Linha 3:

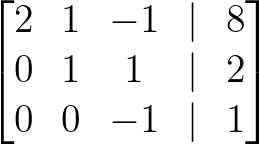
Subtraia 2 × Linha 2. Imagem do autor.

Faça com que o pivô na terceira linha seja positivo:

• Multiplique a linha 3 por -1:

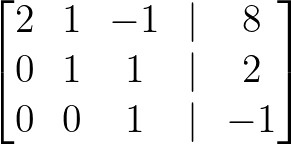
Multiplique a linha 3 por -1. Imagem do autor.

A matriz está agora na forma de escalonamento de linhas.

Etapa 3: Substituição posterior

Agora podemos encontrar os valores de nossas variáveis por meio da substituição reversa:

A partir da fileira 3: 

          z = -1

A partir da linha 2: 

          y + z = 2,

          portanto, y + (-1) = 2,

          o que dá y = 3

A partir da fileira 1: 

          2x + y - z = 8,

          Portanto, 2x + 3 - (-1) = 8,

          o que dá 2x = 4,

          so x = 2

Portanto, a solução é x = 2, y = 3, z = -1.

Embora apliquemos a eliminação gaussiana a esse exemplo, as etapas permanecem as mesmas para outro sistema linear de equações.

Implementação da eliminação gaussiana em Python

Embora possamos escrever o algoritmo usando Python básico, as operações vetorizadas do NumPy tornam a implementação mais limpa e significativamente mais rápida. 

Para fins educacionais, é importante entender o algoritmo subjacente, mas, para uso em produção, recomenda-se aproveitar as bibliotecas otimizadas. Como você já entendeu o algoritmo subjacente na seção anterior, agora vamos nos aprofundar na implementação usando bibliotecas otimizadas em Python.

Implementação baseada em NumPy

O NumPy fornece a função numpy.linalg.solve(), que implementa uma solução altamente otimizada para sistemas de equações lineares:

import numpy as np

# Define the coefficient matrix A and constant vector b
A = np.array([[2, 1, -1],
             [-3, -1, 2],
             [-2, 1, 2]], dtype=float)
b = np.array([8, -11, -3], dtype=float)

# Solve the system Ax = b
x = np.linalg.solve(A, b)

print("Solution:", x)

No código acima, definimos que a matriz de coeficiente A, juntamente com o vetor constante b, é a mesma que a matriz aumentada que criamos na etapa 1 do exemplo de eliminação gaussiana acima. 

Usamos a função numpy.linalg.solve()para chegar à solução e imprimir a saída, conforme mostrado abaixo:

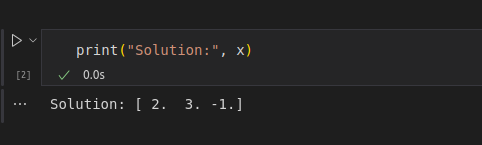
Solução usando a implementação de código. Imagem do autor.

Essa implementação usa o LAPACK como base, que aplica a decomposição LU (uma variante da eliminação gaussiana) otimizada para estabilidade numérica e desempenho.

Tratamento de casos especiais

Ao implementar a eliminação gaussiana, você encontrará vários casos especiais que exigem um tratamento cuidadoso:

• Matrizes singulares: Se o determinante da sua matriz de coeficientes for zero ou muito próximo de zero, o sistema não terá solução ou terá infinitas soluções. A função linalg.solve() do NumPy gera um LinAlgError nesse caso.

• Estabilidade numérica: Com a aritmética de ponto flutuante, os erros de arredondamento podem se acumular e levar a resultados imprecisos. A dinamização parcial, em que o maior elemento de uma coluna é selecionado como pivô, ajuda a atenuar esse problema.

• Sistemas superdeterminados ou subdeterminados: Quando o número de equações não corresponder ao número de variáveis, você pode usar numpy.linalg.lstsq(), que encontra a solução de mínimos quadrados.

Para sistemas grandes com muitos zeros, os solucionadores de matrizes esparsas do SciPy podem ser ordens de magnitude mais rápidos do que os solucionadores densos:

from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

# For large sparse matrices
A_sparse = csr_matrix(A)
x = spsolve(A_sparse, b)

Embora a compreensão da mecânica do algoritmo seja valiosa, na prática, o aproveitamento das implementações otimizadas do NumPy e do SciPy permite que você resolva sistemas lineares de forma eficiente e confiável sem reinventar a roda.

Onde a eliminação gaussiana é usada

A eliminação gaussiana vai muito além da matemática teórica e encontra inúmeras aplicações práticas em vários campos da ciência, engenharia e análise de dados. 

Aqui estão algumas das aplicações mais importantes desse algoritmo fundamental no mundo real:

• Regressão linear: Na ciência de dados, a eliminação gaussiana é usada para resolver as equações normais que surgem ao encontrar os parâmetros de melhor ajuste em modelos de regressão linear. Isso permite que os analistas façam previsões com base em dados históricos.
• Análise de rede: Os engenheiros usam a eliminação gaussiana para resolver correntes ou tensões desconhecidas em circuitos elétricos, aplicando as leis de Kirchhoff, que geram sistemas de equações lineares que devem ser resolvidos simultaneamente.
• Inversão de matriz: A eliminação gaussiana forma a base para o cálculo de inversões de matrizes, que são essenciais em transformações, análises estatísticas e solução de problemas matemáticos complexos em algoritmos de machine learning.
• Integração numérica: Ao implementar métodos numéricos avançados, como Euler implícito ou esquemas de integração Runge-Kutta, a eliminação gaussiana é usada para resolver os sistemas de equações resultantes, garantindo a estabilidade em simulações de sistemas dinâmicos.

Ao compreender esses aplicativos, podemos ver como uma única técnica matemática pode servir de base para muitas das ferramentas usadas diariamente por cientistas de dados, engenheiros e pesquisadores.

Conclusão

Este artigo explorou o algoritmo fundamental de eliminação gaussiana para resolver sistemas de equações lineares transformando matrizes em forma de escalonamento de linhas. Também aprendemos a implementar essa técnica em Python usando as funções otimizadas do NumPy e entendemos suas aplicações práticas em regressão linear, análise de rede, inversão de matriz e métodos numéricos. 

Para aprofundar seu conhecimento sobre álgebra linear e suas aplicações na ciência de dados, considere a possibilidade de se inscrever em nosso curso de Álgebra Linear, no qual você explorará conceitos e implementações mais avançados dessas técnicas fundamentais.