Gaußsche Eliminierung: Eine Methode zum Lösen von Gleichungssystemen

Die Gaußsche Elimination ist einer der grundlegendsten Algorithmen in der linearen Algebra, um lineare Gleichungssysteme zu lösen. Diese nach dem deutschen Mathematiker Carl Friedrich Gauß benannte Methode wandelt ein Gleichungssystem in eine äquivalente, einfachere Form um, indem sie eine Reihe von Operationen an seiner Matrixdarstellung durchführt.

In diesem Artikel erfährst du, wie die Gauß'sche Eliminierung funktioniert, wie sie in Python implementiert wird und welche Anwendungen sie in der Datenwissenschaft und im numerischen Rechnen hat. Wenn wir diesen Algorithmus verstehen, erhalten wir einen Einblick in eine grundlegende Technik, die vielen Berechnungsmethoden in der Datenanalyse zugrunde liegt.

Was ist die Gaußsche Eliminierung?

Die Gaußsche Eliminierung ist ein Algorithmus zur Lösung linearer Gleichungssysteme, bei dem die erweiterte Matrix des Systems systematisch in die Zeilen-Echelon-Form (REF) umgewandelt wird. Durch diese Umwandlung bleibt die Lösungsmenge erhalten, während es einfacher wird, die Werte der Variablen zu finden.

Eine Matrix ist in Zeilen-Echelon-Form, wenn:

• Alle Zeilen, die ausschließlich aus Nullen bestehen, befinden sich am unteren Ende der Matrix
• Der führende Eintrag (erstes Nicht-Null-Element) jeder Nicht-Null-Zeile befindet sich rechts vom führenden Eintrag der Zeile darüber
• Alle Elemente unter einem führenden Eintrag sind Nullen

Um die Reihen-Echelon-Form zu erreichen, verwenden wir drei Arten von elementaren Reihenoperationen:

• Row Swapping: Zwei Reihen austauschen
• Skalierung der Reihen: Multipliziere alle Elemente in einer Zeile mit einer Konstante ungleich Null
• Zeile hinzufügen: Ersetze eine Zeile durch die Summe aus sich selbst und einem Vielfachen einer anderen Zeile

Außerdem ist es wichtig, zwischen Gauß-Elimination und Gauß-Jordan-Elimination zu unterscheiden:

• Gaußsche Eliminierung wandelt die Matrix in die Zeilen-Echelon-Form um und erfordert eine Rücksubstitution, um die Variablenwerte zu finden
• Gauß-Jordan-Elimination setzt den Prozess fort, um die Zeilen-Echelon-Form (RREF) zu reduzieren, bei der alle führenden Einträge 1 sind und alle anderen Einträge in jeder Spalte des führenden Eintrags 0 sind

Während die Gauß-Jordan-Elimination eine direktere Lösung bietet, ist die Gauß-Elimination bei großen Systemen in der Regel effizienter, vor allem in Kombination mit der Rücksubstitution und Techniken wie der LU-Zerlegung.

Schritt-für-Schritt-Aufschlüsselung des Gaußschen Eliminierungsalgorithmus

Lass uns den Gaußschen Eliminierungsprozess anhand eines einfachen Beispiels durchgehen. Betrachte das folgende System von linearen Gleichungen:

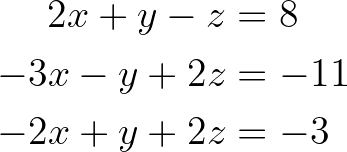
System von linearen Gleichungen. Bild vom Autor.

Schritt 1: Erstelle die erweiterte Matrix

Zunächst stellen wir das System als augmentierte Matrix dar, indem wir die Koeffizientenmatrix mit den Konstanten kombinieren:

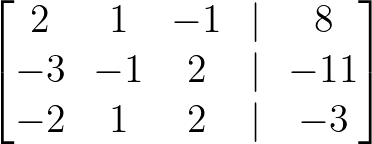
Erhöhte Matrix. Bild vom Autor.

Schritt 2: Vorwärts-Eliminierung

Jetzt führen wir elementare Zeilenoperationen durch, um die Matrix in die Zeilen-Echelon-Form umzuwandeln.

Mache das erste Element der ersten Spalte zum Drehpunkt und eliminiere alle Elemente darunter:

• Addiere 3/2 × Reihe 1 zu Reihe 2:

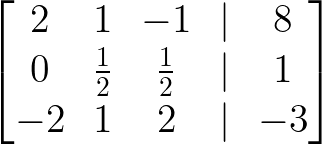
Addiere 3/2 × Reihe 1 zu Reihe 2. Bild vom Autor.

• Füge Reihe 1 zu Reihe 3 hinzu:

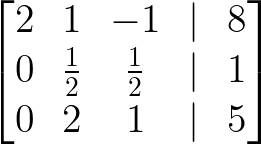
Füge Reihe 1 zu Reihe 3 hinzu. Bild vom Autor.

Gehe zur zweiten Spalte und eliminiere alle Elemente unterhalb des Drehpunkts:

• Multipliziere Zeile 2 mit 2, um den Drehpunkt 1 zu erhalten:

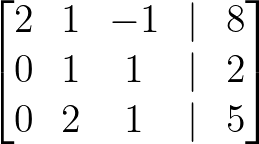
Multipliziere Zeile 2 mit 2. Bild vom Autor.

• Ziehe 2 × Zeile 2 von Zeile 3 ab:

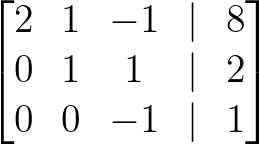
Ziehe 2 × Zeile 2 ab. Bild vom Autor.

Mache den Drehpunkt in der dritten Reihe positiv:

• Multipliziere Zeile 3 mit -1:

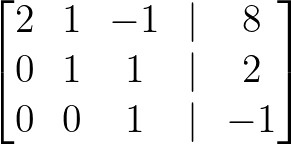
Multipliziere Zeile 3 mit -1. Bild vom Autor.

Die Matrix hat jetzt die Zeilen-Echelon-Form.

Schritt 3: Back-Substitution

Jetzt können wir die Werte unserer Variablen durch Rücksubstitution ermitteln:

Ab Reihe 3: 

          z = -1

Ab Reihe 2: 

          y + z = 2,

          also ist y + (-1) = 2,

          das ergibt y = 3

Ab Reihe 1: 

          2x + y - z = 8,

          also 2x + 3 - (-1) = 8,

          was 2x = 4 ergibt,

          so x = 2

Die Lösung ist also x = 2, y = 3, z = -1.

Während wir in diesem Beispiel die Gaußsche Eliminierung anwenden, bleiben die Schritte für ein anderes lineares Gleichungssystem dieselben.

Implementierung der Gaußschen Eliminierung in Python

Wir können den Algorithmus zwar auch mit Python schreiben, aber die vektorisierten Operationen von NumPy machen die Implementierung sowohl sauberer als auch deutlich schneller. 

Für Bildungszwecke ist es wichtig, den zugrunde liegenden Algorithmus zu verstehen, aber für den Einsatz in der Produktion wird empfohlen, optimierte Bibliotheken zu verwenden. Nachdem wir im vorherigen Abschnitt bereits den zugrunde liegenden Algorithmus verstanden haben, werden wir uns nun mit der Implementierung mithilfe optimierter Bibliotheken in Python beschäftigen.

NumPy-basierte Implementierung

NumPy bietet die Funktion numpy.linalg.solve(), die eine hochoptimierte Lösung für lineare Gleichungssysteme implementiert:

import numpy as np

# Define the coefficient matrix A and constant vector b
A = np.array([[2, 1, -1],
             [-3, -1, 2],
             [-2, 1, 2]], dtype=float)
b = np.array([8, -11, -3], dtype=float)

# Solve the system Ax = b
x = np.linalg.solve(A, b)

print("Solution:", x)

Im obigen Code definieren wir die Koeffizientenmatrix A und den Konstantenvektor b genauso wie die erweiterte Matrix, die wir in Schritt 1 des obigen Beispiels zur Gauß-Elimination erstellt haben. 

Wir verwenden die Funktion numpy.linalg.solve(), um die Lösung zu finden, und drucken die Ausgabe wie unten gezeigt aus:

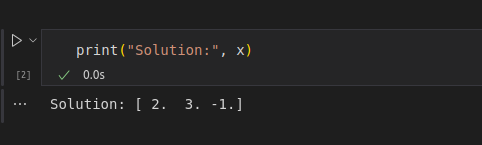
Lösung durch Code-Implementierung. Bild vom Autor.

Diese Implementierung verwendet LAPACK, das die LU-Zerlegung (eine Variante der Gauß'schen Eliminierung) anwendet und für numerische Stabilität und Leistung optimiert ist.

Umgang mit Sonderfällen

Bei der Umsetzung der Gaußschen Eliminierung gibt es einige Sonderfälle, die eine sorgfältige Handhabung erfordern:

• Singuläre Matrizen: Wenn die Determinante deiner Koeffizientenmatrix null oder sehr nah an null ist, hat das System entweder keine Lösung oder unendlich viele Lösungen. Die Funktion linalg.solve() von NumPy löst in diesem Fall eine LinAlgError aus.

• Numerische Stabilität: Bei der Fließkommaarithmetik können sich Rundungsfehler ansammeln und zu ungenauen Ergebnissen führen. Das partielle Pivoting, bei dem das größte Element in einer Spalte als Pivot ausgewählt wird, hilft, dieses Problem zu entschärfen.

• Überdeterminierte oder unterdeterminierte Systeme: Wenn die Anzahl der Gleichungen nicht mit der Anzahl der Variablen übereinstimmt, kannst du stattdessen numpy.linalg.lstsq() verwenden, das die Lösung mit den kleinsten Quadraten findet.

Bei großen Systemen mit vielen Nullen können die spärlichen Matrixlöser von SciPy um Größenordnungen schneller sein als dichte Löser:

from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

# For large sparse matrices
A_sparse = csr_matrix(A)
x = spsolve(A_sparse, b)

Es ist zwar wichtig, die Mechanismen des Algorithmus zu verstehen, aber in der Praxis kannst du mit den optimierten Implementierungen von NumPy und SciPy lineare Systeme effizient und zuverlässig lösen, ohne das Rad neu erfinden zu müssen.

Wo die Gaußsche Eliminierung verwendet wird

Die Gaußsche Eliminierung geht weit über die theoretische Mathematik hinaus und findet zahlreiche praktische Anwendungen in verschiedenen Bereichen der Wissenschaft, Technik und Datenanalyse. 

Hier sind einige der wichtigsten Anwendungen dieses grundlegenden Algorithmus in der Praxis:

• Lineare Regression: In der Datenwissenschaft wird die Gaußsche Eliminierung verwendet, um die Normalgleichungen zu lösen, die bei der Suche nach den am besten passenden Parametern in linearen Regressionsmodellen auftreten. So können Analysten Vorhersagen auf der Grundlage historischer Daten treffen.
• Netzwerkanalyse: Ingenieure verwenden die Gaußsche Eliminierung, um unbekannte Ströme oder Spannungen in elektrischen Schaltkreisen zu lösen, indem sie die Kirchhoff'schen Gesetze anwenden , die Systeme von linearen Gleichungen erzeugen, die gleichzeitig gelöst werden müssen.
• Matrix-Inversion: Die Gaußsche Eliminierung bildet die Grundlage für die Berechnung von Matrixinversionen, die für Transformationen, statistische Analysen und die Lösung komplexer mathematischer Probleme in maschinellen Lernalgorithmen unerlässlich sind.
• Numerische Integration: Bei der Implementierung fortschrittlicher numerischer Methoden wie impliziter Euler- oder Runge-Kutta-Integrationsverfahren wird die Gaußsche Eliminierung zur Lösung der resultierenden Gleichungssysteme verwendet, um die Stabilität bei Simulationen dynamischer Systeme zu gewährleisten.

Wenn wir diese Anwendungen verstehen, können wir sehen, wie eine einzige mathematische Technik als Rückgrat für viele der Werkzeuge dienen kann, die von Datenwissenschaftlern, Ingenieuren und Forschern täglich verwendet werden.

Fazit

In diesem Artikel wurde der grundlegende Algorithmus der Gaußschen Eliminierung zur Lösung von linearen Gleichungssystemen durch die Umwandlung von Matrizen in die Zeilen-Echelon-Form untersucht. Wir lernten auch, wie man diese Technik mit den optimierten Funktionen von NumPy in Python implementiert, und wir verstanden ihre praktischen Anwendungen in der linearen Regression, der Netzwerkanalyse, der Matrixinversion und den numerischen Methoden. 

Wenn du deine Kenntnisse der linearen Algebra und ihrer Anwendungen in den Datenwissenschaften vertiefen möchtest, solltest du dich für unseren Kurs Lineare Algebra anmelden, in dem du fortgeschrittene Konzepte und Implementierungen dieser grundlegenden Techniken kennenlernst.