Eliminación gaussiana: Un método para resolver sistemas de ecuaciones

La eliminación de Gauss es uno de los algoritmos más fundamentales del álgebra lineal para resolver sistemas de ecuaciones lineales. Este método, que debe su nombre al matemático alemán Carl Friedrich Gauss, transforma un sistema de ecuaciones en una forma equivalente más sencilla realizando una secuencia de operaciones sobre su representación matricial.

Este artículo explorará cómo funciona la eliminación gaussiana, la implementará en Python y examinará sus aplicaciones en la ciencia de datos y la computación numérica. Al comprender este algoritmo, conoceremos una técnica fundamental en la que se basan muchos métodos computacionales utilizados en el análisis de datos.

¿Qué es la eliminación gaussiana?

La eliminación gaussiana es un algoritmo para resolver sistemas de ecuaciones lineales transformando sistemáticamente la matriz aumentada del sistema en forma escalonada (REF). Esta transformación preserva el conjunto de soluciones a la vez que facilita la búsqueda de los valores de las variables.

Una matriz está en forma escalonada cuando:

• Todas las filas formadas totalmente por ceros están en la parte inferior de la matriz
• La entrada principal (primer elemento distinto de cero) de cada fila distinta de cero está a la derecha de la entrada principal de la fila superior
• Todos los elementos por debajo de una entrada inicial son ceros

Para conseguir la forma escalonada de fila, utilizamos tres tipos de operaciones elementales de fila:

• Intercambio de filas: Intercambia dos filas
• Escalado de filas: Multiplica todos los elementos de una fila por una constante distinta de cero
• Adición de filas: Sustituye una fila por la suma de sí misma y un múltiplo de otra fila

Además, es importante distinguir entre la eliminación de Gauss y la eliminación de Gauss-Jordan:

• Eliminación gaussiana transforma la matriz en forma escalonada, lo que requiere una sustitución inversa para encontrar los valores de las variables
• Eliminación de Gauss-Jordan continúa el proceso para reducir la forma escalonada de fila (RREF), en la que todas las entradas principales son 1 y todas las demás entradas de la columna de cada entrada principal son 0

Aunque la eliminación de Gauss-Jordan proporciona una solución más directa, la eliminación de Gauss suele ser más eficaz para los sistemas grandes, sobre todo si se combina con la sustitución inversa y técnicas como la descomposición LU.

Desglose paso a paso del algoritmo de eliminación gaussiana

Recorramos el proceso de eliminación gaussiana con un ejemplo sencillo. Considera el siguiente sistema de ecuaciones lineales:

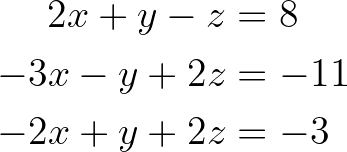
Sistema de ecuaciones lineales. Imagen del autor.

Paso 1: Crea la matriz aumentada

En primer lugar, representamos el sistema como una matriz aumentada, combinando la matriz de coeficientes con las constantes:

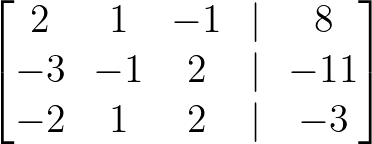
Matriz aumentada. Imagen del autor.

Paso 2: Eliminación hacia delante

Ahora realizaremos operaciones elementales de fila para transformar la matriz en forma escalonada de fila.

Haz que el primer elemento de la primera columna sea un pivote y elimina todos los elementos por debajo de él:

• Añade 3/2 × Fila 1 a la Fila 2:

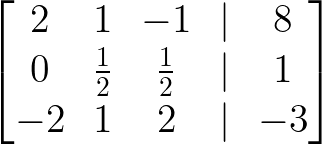
Añade 3/2 × Fila 1 a la Fila 2. Imagen del autor.

• Añade la Fila 1 a la Fila 3:

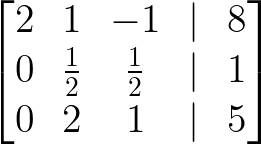
Añade la Fila 1 a la Fila 3. Imagen del autor.

Pasa a la segunda columna y elimina todos los elementos por debajo del pivote:

• Multiplica la Fila 2 por 2 para hacer el pivote 1:

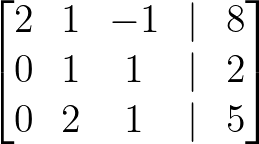
Multiplica la Fila 2 por 2. Imagen del autor.

• Resta 2 × Fila 2 de la Fila 3:

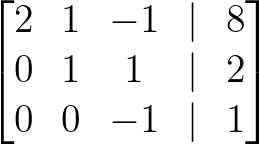
Resta 2 × Fila 2. Imagen del autor.

Haz que el pivote de la tercera fila sea positivo:

• Multiplica la Fila 3 por -1:

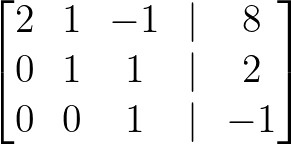
Multiplica la Fila 3 por -1. Imagen del autor.

La matriz está ahora en forma escalonada.

Paso 3: Sustitución inversa

Ahora podemos encontrar los valores de nuestras variables mediante la sustitución inversa:

Desde la Fila 3: 

z = -1

Desde la Fila 2: 

y + z = 2,
so y + (-1) = 2,
which gives y = 3

Desde la Fila 1: 

2x + y - z = 8,
so 2x + 3 - (-1) = 8,
which gives 2x = 4,
so x = 2

Por tanto, la solución es x = 2, y = 3, z = -1.

Aunque apliquemos la eliminación de Gauss a este ejemplo, los pasos siguen siendo los mismos para otro sistema lineal de ecuaciones.

Implementación de la eliminación gaussiana en Python

Aunque podemos escribir el algoritmo utilizando Python básico, las operaciones vectorizadas de NumPy hacen que la implementación sea más limpia y significativamente más rápida. 

Para fines educativos, comprender el algoritmo subyacente es valioso, pero para uso en producción, se recomienda aprovechar las bibliotecas optimizadas. Habiendo comprendido ya el algoritmo subyacente en la sección anterior, nos adentraremos ahora en la implementación utilizando bibliotecas optimizadas en Python.

Implementación basada en NumPy

NumPy proporciona la función numpy.linalg.solve(), que implementa una solución altamente optimizada para sistemas de ecuaciones lineales:

import numpy as np

# Define the coefficient matrix A and constant vector b
A = np.array([[2, 1, -1],
             [-3, -1, 2],
             [-2, 1, 2]], dtype=float)
b = np.array([8, -11, -3], dtype=float)

# Solve the system Ax = b
x = np.linalg.solve(A, b)

print("Solution:", x)

En el código anterior, definimos la matriz de coeficientes A, junto con el vector constante b, son iguales que la matriz aumentada que creamos en el paso 1 del ejemplo de eliminación gaussiana anterior. 

Utilizamos la función numpy.linalg.solve()para llegar a la solución e imprimimos el resultado como se ve a continuación:

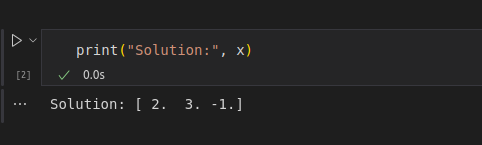
Solución mediante aplicación de código. Imagen del autor.

Esta implementación utiliza LAPACK bajo el capó, que aplica la descomposición LU (una variante de la eliminación gaussiana) optimizada para la estabilidad numérica y el rendimiento.

Tratamiento de casos especiales

Al aplicar la eliminación gaussiana, te encontrarás con varios casos especiales que requieren un manejo cuidadoso:

• Matrices singulares: Si el determinante de tu matriz de coeficientes es cero o muy próximo a cero, el sistema no tiene solución o tiene infinitas soluciones. La función linalg.solve() de NumPy plantea un LinAlgError en este caso.

• Estabilidad numérica: Con la aritmética de coma flotante, los errores de redondeo pueden acumularse y dar lugar a resultados inexactos. El pivotaje parcial, en el que el elemento más grande de una columna se selecciona como pivote, ayuda a mitigar este problema.

• Sistemas sobredeterminados o infradeterminados: Cuando el número de ecuaciones no coincide con el número de variables, puedes utilizar numpy.linalg.lstsq(), que encuentra la solución por mínimos cuadrados.

Para sistemas grandes con muchos ceros, los solucionadores de matrices dispersas de SciPy pueden ser órdenes de magnitud más rápidos que los solucionadores densos:

from scipy.sparse import csr_matrix
from scipy.sparse.linalg import spsolve

# For large sparse matrices
A_sparse = csr_matrix(A)
x = spsolve(A_sparse, b)

Aunque comprender la mecánica del algoritmo es valioso, en la práctica, aprovechar las implementaciones optimizadas de NumPy y SciPy te permite resolver sistemas lineales de forma eficaz y fiable sin reinventar la rueda.

Dónde se utiliza la eliminación gaussiana

La eliminación gaussiana va mucho más allá de las matemáticas teóricas y encuentra numerosas aplicaciones prácticas en diversos campos de la ciencia, la ingeniería y el análisis de datos. 

He aquí algunas de las aplicaciones más importantes de este algoritmo fundamental en el mundo real:

• Regresión lineal: En la ciencia de datos, la eliminación gaussiana se utiliza para resolver las ecuaciones normales que surgen al encontrar los parámetros que mejor se ajustan en los modelos de regresión lineal. Esto permite a los analistas hacer predicciones basadas en datos históricos.
• Análisis de redes: Los ingenieros utilizan la eliminación de Gauss para resolver corrientes o tensiones desconocidas en circuitos eléctricos aplicando las leyes de Kirchhoff, que generan sistemas de ecuaciones lineales que deben resolverse simultáneamente.
• Inversión matricial: La eliminación gaussiana constituye la base para calcular las inversiones de matrices, que son esenciales en las transformaciones, los análisis estadísticos y la resolución de problemas matemáticos complejos en los algoritmos de aprendizaje automático.
• Integración numérica: Al aplicar métodos numéricos avanzados, como los esquemas de integración implícitos de Euler o Runge-Kutta, se utiliza la eliminación gaussiana para resolver los sistemas de ecuaciones resultantes, lo que garantiza la estabilidad en las simulaciones de sistemas dinámicos.

Al comprender estas aplicaciones, podemos ver cómo una única técnica matemática puede servir de columna vertebral para muchas de las herramientas que utilizan a diario los científicos de datos, los ingenieros y los investigadores.

Conclusión

Este artículo explora el algoritmo fundamental de eliminación de Gauss para resolver sistemas de ecuaciones lineales mediante la transformación de matrices en forma escalonada. También aprendimos a implementar esta técnica en Python utilizando las funciones optimizadas de NumPy, y comprendimos sus aplicaciones prácticas en regresión lineal, análisis de redes, inversión de matrices y métodos numéricos. 

Para profundizar en tu conocimiento del álgebra lineal y sus aplicaciones en la ciencia de datos, considera la posibilidad de matricularte en nuestro curso de Álgebra Lineal, donde explorarás conceptos e implementaciones más avanzadas de estas técnicas fundamentales.