Moyenne géométrique : Une mesure de la croissance et de l'effet d'entraînement

Vous est-il déjà arrivé de calculer la moyenne des rendements annuels de vos investissements et de constater que votre rendement global réel ne correspondait pas tout à fait à cette moyenne ? Ce scénario courant en finance souligne l'importance de comprendre et d'appliquer la moyenne géométrique - une mesure utile qui s'avère souvent plus appropriée que la moyenne arithmétique largement utilisée lorsqu'il s'agit de taux de changement et d'effets composés.

Dans ce tutoriel, nous allons explorer le concept de moyenne géométrique et son rôle dans l'analyse des données, en particulier dans des domaines tels que la finance, la biologie et la science des données. Nous examinerons également les scénarios dans lesquels elle est plus performante que d'autres mesures de la tendance centrale.

Qu'est-ce que la moyenne géométrique ?

La moyenne géométrique est un type de moyenne particulièrement utile lorsque l'on travaille avec des ensembles de nombres positifs, notamment ceux qui impliquent une multiplication ou une croissance exponentielle. Contrairement à la moyenne arithmétique, plus courante, qui additionne les nombres et les divise par le nombre, la moyenne géométrique est particulièrement adaptée au traitement d'ensembles de données impliquant des relations multiplicatives ou une croissance exponentielle.

Voici quelques-uns des domaines dans lesquels la moyenne géométrique est utile :

1. Finance: Il est couramment utilisé pour calculer les taux de rendement moyens sur plusieurs périodes. Contrairement à la moyenne arithmétique, la moyenne géométrique tient compte de la capitalisation, ce qui la rend plus précise pour les calculs financiers.
2. Biologie: Dans les études sur la croissance démographique, la moyenne géométrique est utilisée pour calculer les taux de croissance moyens dans le temps.
3. Géométrie: L'un de ses aspects les plus élégants se trouve dans les triangles droits, où l'altitude de l'hypoténuse incarne la moyenne géométrique des segments qu'elle crée sur cette hypoténuse. En outre, la moyenne géométrique représente la longueur du côté d'un carré qui aurait la même surface qu'un rectangle donné, ce qui permet de "quadriller" les surfaces rectangulaires.

Comme vous pouvez le constater, la moyenne géométrique est un outil précieux pour les calculs quotidiens, mais aussi pour des concepts mathématiques plus abstraits.

Comment calculer la moyenne géométrique

Il existe plusieurs méthodes pour calculer la moyenne géométrique, chacune ayant ses propres avantages en fonction de la situation.

La formule de la moyenne géométrique

La façon la plus simple de calculer la moyenne géométrique est d'utiliser la formule standard : 

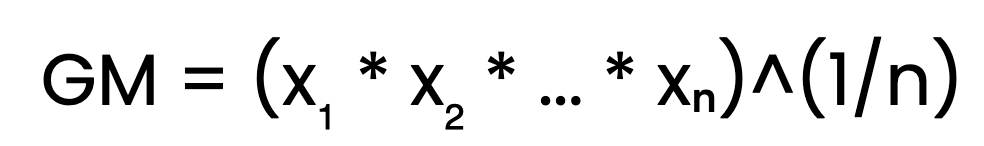
Ici, x₁, x₂, ..., xₙ sont les nombres positifs de l'ensemble de données, et n est le nombre de nombres. Pour obtenir la moyenne géométrique, nous multiplions toutes les valeurs et prenons la racine nième du produit, où n est le nombre de valeurs. Voyons cela à travers un exemple. Considérez les nombres 2, 4 et 8. Trouver leur moyenne géométrique :

1. Multipliez les chiffres : 2 * 4 * 8 = 64
2. Prenez la racine cubique (puisqu'il y a 3 nombres) : ∛64 ≈ 4

La moyenne géométrique de 2, 4 et 8 est 4. Ce résultat nous indique que si nous avions trois nombres égaux, chacun égal à 4, leur produit serait le même que le produit des nombres initiaux. Essentiellement, 4 est le facteur de croissance cohérent pour les trois valeurs.

Calcul de la moyenne géométrique par addition des logarithmes

Pour les ensembles de données plus importants ou pour éviter les erreurs de débordement lorsque l'on traite de très grands nombres, nous pouvons utiliser des logarithmes. Cette méthode simplifie la multiplication en addition et rend les calculs plus faciles à gérer. Ici, nous prenons d'abord le logarithme de chaque nombre, nous calculons la moyenne arithmétique de ces logarithmes, puis nous prenons l'antilog (exponentielle) de cette moyenne. Reprenons l'exemple précédent. 

1. Prenez des logarithmes (base 10) : log(2) ≈ 0.3010, log(4) ≈ 0.6021, log(8) ≈ 0.9031
2. Calculez la moyenne arithmétique : (0.3010 + 0.6021 + 0.9031) / 3 ≈ 0.6021
3. Prenez l'antilog : (10^x) = 10^0.6021 ≈ 4

Cette méthode nous donne le même résultat que la méthode de calcul direct. Vous pouvez utiliser des logarithmes de n'importe quelle base (tels que les logarithmes naturels de base e), à condition d'utiliser la même base tout au long du calcul. La moyenne géométrique finale sera la même.

Moyenne géométrique dans la science des données et l'apprentissage automatique

La moyenne géométrique est une mesure statistique utile qui a plusieurs applications importantes en science des données et en apprentissage automatique. Voici trois cas d'utilisation clés où la moyenne géométrique s'avère précieuse. 

Taux de croissance et analyse des séries chronologiques

En science des données, nous analysons souvent les taux de croissance au fil du temps, comme dans la dynamique des populations, les tendances du marché ou les taux d'adoption par les utilisateurs. La moyenne géométrique est idéale pour ces situations, car elle rend compte avec précision de la nature composée de la croissance. Contrairement à la moyenne arithmétique, qui se contente de faire la moyenne des taux sans tenir compte de la façon dont la croissance de chaque année s'ajoute à celle de la précédente, la moyenne géométrique tient compte de cet effet de composition.

Imaginez que vous analysiez le taux de croissance annuel de la base d'utilisateurs d'une startup sur cinq ans : 20 %, 15 %, 25 %, 10 % et 30 %. Si la moyenne arithmétique (20 %) peut sembler une solution rapide, elle ne tient pas compte de l'effet de composition. La moyenne géométrique ((1,20 * 1,15 * 1,25 * 1,10 * 1,30)^(1/5) - 1 ≈ 19,77%) fournit un taux de croissance moyen plus précis qui, s'il était appliqué de manière cohérente chaque année, donnerait la même valeur finale que les différents taux de croissance réels.

Analyse statistique des données asymétriques

En science des données, nous avons souvent affaire à des ensembles de données qui sont positivement asymétriques en raison de processus multiplicatifs, tels que les niveaux de revenus, les mesures biologiques ou certains indicateurs financiers. Dans ce cas, l'utilisation de la moyenne arithmétique peut être trompeuse car elle est sensible aux valeurs extrêmes (aberrations), qui peuvent fausser la représentation de la tendance centrale.

La moyenne géométrique est particulièrement utile lorsqu'il s'agit de données qui suivent une distribution log-normale. Voici pourquoi :

• Minimise l'influence des valeurs aberrantes : La moyenne géométrique réduit l'impact des valeurs extrêmement élevées ou faibles et fournit une valeur centrale plus représentative pour les données asymétriques.
• Gère les relations multiplicatives : Elle est appropriée pour les données où les valeurs sont combinées de manière multiplicative plutôt qu'additive.

Considérez un ensemble de données sur les revenus des ménages dans une région où la plupart des ménages gagnent entre 30 000 et 60 000 dollars, mais où quelques-uns gagnent plus d'un million de dollars.

• Moyenne arithmétique des revenus : Ce chiffre sera fortement influencé par les valeurs aberrantes des hauts revenus, ce qui pourrait suggérer un revenu moyen beaucoup plus élevé que celui de la plupart des gens.
• Moyenne géométrique des revenus : On obtient ainsi une valeur centrale qui reflète plus précisément le revenu type en minimisant l'influence des valeurs extrêmes.

En utilisant la moyenne géométrique dans de tels cas, les scientifiques des données peuvent obtenir une mesure plus précise de la tendance centrale, ce qui permet d'obtenir de meilleures informations et des analyses plus fiables. La moyenne géométrique est donc un outil essentiel lorsque l'on travaille avec des distributions de données asymétriques dans différents domaines.

Mesures d'évaluation pour les ensembles de données déséquilibrés

Dans les tâches de classification, nous rencontrons souvent des ensembles de données déséquilibrés où certains groupes sont représentés par un nombre beaucoup plus important d'exemples que d'autres. Dans ce cas, les mesures d'évaluation traditionnelles telles que la précision peuvent être trompeuses. C'est là que la moyenne géométrique, ou G-Mean, devient un outil précieux.

La moyenne G est la racine du produit de la sensibilité par classe (rappel). Pour la classification binaire, c'est la racine carrée du produit de la sensibilité et de la spécificité. Pour les problèmes multi-classes, il s'agit d'une racine supérieure du produit de la sensibilité pour chaque classe.

G-Mean vise à équilibrer la précision entre toutes les classes, ce qui le rend particulièrement utile pour les ensembles de données déséquilibrés. Cependant, il est important de noter que le G-Mean n'est pas défini lorsqu'une classe a une sensibilité nulle, ce qui limite son applicabilité dans les scénarios de déséquilibre extrême. Dans la pratique, des versions modifiées ou des mesures alternatives peuvent être utilisées pour remédier à cette limitation.

Pour en savoir plus sur la façon dont la moyenne géométrique et d'autres mesures statistiques sont appliquées dans l'apprentissage automatique, envisagez d'explorer notre piste de carrière Machine Learning Scientist with Python, qui offre des cours approfondis qui couvrent les concepts et les techniques essentiels de l'apprentissage automatique, avec des aperçus pratiques et une expérience concrète.