Media geométrica: Una medida para el crecimiento y la capitalización

¿Has calculado alguna vez la media de los rendimientos anuales de tus inversiones, sólo para descubrir que tu rendimiento global real no coincide del todo? Este escenario habitual en finanzas pone de relieve la importancia de comprender y aplicar la media geométrica, una medida útil que a menudo resulta más apropiada que la media aritmética, ampliamente utilizada, cuando se trata de tasas de cambio y efectos compuestos.

En este tutorial, exploraremos el concepto de media geométrica y su papel en el análisis de datos, especialmente en campos como las finanzas, la biología y la ciencia de datos. También examinaremos los escenarios en los que supera a otras medidas de tendencia central.

¿Qué es la media geométrica?

La media geométrica es un tipo de media especialmente útil cuando se trabaja con conjuntos de números positivos, sobre todo los que implican multiplicación o crecimiento exponencial. A diferencia de la media aritmética más común, que suma números y los divide por el recuento, la media geométrica es especialmente adecuada para manejar conjuntos de datos que implican relaciones multiplicativas o crecimiento exponencial.

He aquí algunos campos en los que la media geométrica es valiosa:

1. Finanzas: Se suele utilizar para calcular tasas medias de rentabilidad a lo largo de varios periodos. A diferencia de la media aritmética, la media geométrica tiene en cuenta la capitalización, lo que la hace más precisa para los cálculos financieros.
2. Biología: En los estudios sobre el crecimiento de la población, se utiliza la media geométrica para calcular las tasas medias de crecimiento a lo largo del tiempo.
3. Geometría: Una de sus apariciones más elegantes es en los triángulos rectángulos, donde la altura a la hipotenusa encarna la media geométrica de los segmentos que crea en esa hipotenusa. Además, la media geométrica representa la longitud lateral de un cuadrado que tendría la misma área que un rectángulo dado, proporcionando una forma de "cuadrar" áreas rectangulares.

Como puedes ver, la media geométrica es una herramienta valiosa tanto en los cálculos cotidianos como en conceptos matemáticos más abstractos.

Cómo calcular la media geométrica

Existen varios métodos para calcular la media geométrica, cada uno con sus propias ventajas según la situación.

La fórmula de la media geométrica

La forma más sencilla de calcular la media geométrica es utilizando la fórmula estándar: 

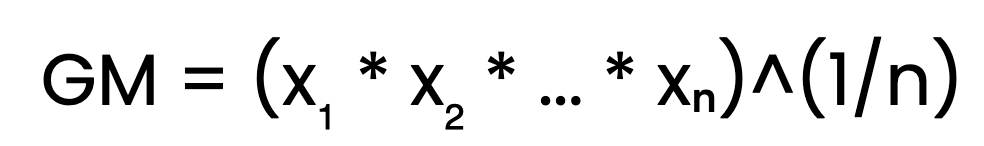
Aquí, x₁, x₂, ..., xₙ son los números positivos del conjunto de datos, y n es el recuento de números. Para obtener la media geométrica multiplicamos todos los valores juntos y tomamos la raíz enésima del producto, donde n es el número de valores. Veámoslo con un ejemplo. Considera los números 2, 4 y 8. Para hallar su media geométrica:

1. Multiplica los números: 2 * 4 * 8 = 64
2. Saca la raíz cúbica (ya que hay 3 números): ∛64 ≈ 4

La media geométrica de 2, 4 y 8 es 4. Este resultado nos dice que si tuviéramos tres números iguales, cada uno igual a 4, su producto sería igual al producto de los números originales. Esencialmente, 4 es el factor de crecimiento constante en los tres valores.

Calcular la media geométrica sumando logaritmos

Para conjuntos de datos más grandes o para evitar errores de desbordamiento al tratar con números muy grandes, podemos utilizar logaritmos. Este método simplifica la multiplicación en suma y hace que los cálculos sean más manejables. Aquí, primero tomamos el logaritmo de cada número, calculamos la media aritmética de estos logaritmos y, a continuación, tomamos el antilog (exponencial) de esta media. Utilicemos el mismo ejemplo anterior. 

1. Toma logaritmos (base 10): log(2) ≈ 0,3010, log(4) ≈ 0,6021, log(8) ≈ 0,9031
2. Calcula la media aritmética: (0.3010 + 0.6021 + 0.9031) / 3 ≈ 0.6021
3. Toma el antilog: (10^x) = 10^0.6021 ≈ 4

Este método nos da el mismo resultado que el método de cálculo directo. Puedes utilizar logaritmos de cualquier base (como los logaritmos naturales de base e), siempre que utilices la misma base en todo el cálculo. La media geométrica final será la misma.

La media geométrica en la ciencia de datos y el aprendizaje automático

La media geométrica es una medida estadística útil con varias aplicaciones importantes en la ciencia de datos y el aprendizaje automático. He aquí tres casos de uso clave en los que la media geométrica resulta valiosa. 

Tasas de crecimiento y análisis de series temporales

En la ciencia de datos, a menudo analizamos las tasas de crecimiento a lo largo del tiempo, como en la dinámica de la población, las tendencias del mercado o las tasas de adopción de usuarios. La media geométrica es ideal para estas situaciones porque capta con precisión la naturaleza compuesta del crecimiento. A diferencia de la media aritmética, que simplemente promedia las tasas sin tener en cuenta cómo el crecimiento de cada año se basa en el anterior, la media geométrica tiene en cuenta este efecto compuesto.

Imagina que estás analizando la tasa de crecimiento anual de la base de usuarios de una startup durante cinco años: 20%, 15%, 25%, 10% y 30%. Aunque la media aritmética (20%) pueda parecer una solución rápida, no tiene en cuenta el efecto compuesto. La media geométrica ((1,20 * 1,15 * 1,25 * 1,10 * 1,30)^(1/5) - 1 ≈ 19,77%) proporciona una tasa de crecimiento medio más precisa que, si se aplicara sistemáticamente cada año, daría como resultado el mismo valor final que las tasas de crecimiento variadas reales.

Análisis estadístico de datos sesgados

En la ciencia de datos, a menudo tratamos con conjuntos de datos que están sesgados positivamente debido a procesos multiplicativos, como los niveles de ingresos, las mediciones biológicas o determinados indicadores financieros. En estos casos, utilizar la media aritmética puede ser engañoso porque es sensible a los valores extremos (valores atípicos), que pueden distorsionar la representación de la tendencia central.

La media geométrica es especialmente útil cuando se trata de datos que siguen una distribución log-normal. He aquí por qué:

• Minimiza la influencia de los valores atípicos: La media geométrica reduce el impacto de los valores extremadamente altos o bajos, proporcionando un valor central más representativo para los datos sesgados.
• Maneja relaciones multiplicativas: Es adecuado para datos en los que los valores se combinan multiplicativamente en lugar de aditivamente.

Considera un conjunto de datos de ingresos familiares en una región donde la mayoría de los hogares ganan entre 30.000 y 60.000 $, pero unos pocos ganan más de 1 millón de $.

• Media aritmética de los ingresos: Esto se verá muy influido por los valores atípicos de ingresos elevados, lo que podría sugerir unos ingresos medios muy superiores a los que gana la mayoría de la gente.
• Ingresos medios geométricos: Así se obtiene un valor central que refleja la renta típica con mayor precisión, al minimizar la influencia de los valores extremos.

Al utilizar la media geométrica en estos casos, los científicos de datos pueden obtener una medida más precisa de la tendencia central, lo que permite obtener mejores perspectivas y análisis más fiables. Esto hace que la media geométrica sea una herramienta esencial cuando se trabaja con distribuciones de datos sesgadas en diversos campos.

Métricas de evaluación para conjuntos de datos desequilibrados

En las tareas de clasificación, a menudo nos encontramos con conjuntos de datos desequilibrados en los que algunos grupos están representados por un número de ejemplos mucho mayor que otros. En estos casos, las métricas de evaluación tradicionales, como la precisión, pueden ser engañosas. Aquí es donde la puntuación media geométrica, o media G, se convierte en una herramienta valiosa.

La media G es la raíz del producto de la sensibilidad por clases (recall). Para la clasificación binaria, es la raíz cuadrada del producto de la sensibilidad y la especificidad. Para los problemas multiclase, es una raíz superior del producto de la sensibilidad de cada clase.

G-Mean pretende equilibrar la precisión entre todas las clases, por lo que resulta especialmente útil para conjuntos de datos desequilibrados. Sin embargo, es importante tener en cuenta que la Media-G es indefinida cuando cualquier clase tiene sensibilidad cero, lo que limita su aplicabilidad en escenarios de desequilibrio extremo. En la práctica, pueden utilizarse versiones modificadas o métricas alternativas para abordar esta limitación.

Para saber más sobre cómo se aplican la media geométrica y otras medidas estadísticas en el aprendizaje automático, considera explorar nuestra trayectoria profesional de Científico de Aprendizaje Automático con Python, que ofrece una lección en profundidad que cubre conceptos y técnicas esenciales de aprendizaje automático, con conocimientos prácticos y experiencia práctica.